往复压缩机管路中T型三通的气流脉动动力学特征研究①

刘丽思 张 杨 付玉东 杨国安

(北京化工大学机电工程学院)

往复压缩机管路中T型三通的气流脉动动力学特征研究①

刘丽思 张 杨 付玉东 杨国安

(北京化工大学机电工程学院)

往复压缩机间歇性吸、排气的工作特性，使管网内形成压力和速度呈周期性变化的气流脉动成为激发管网振动的主要原因，严重影响了压缩机组的平稳运行。以平面波动理论为基础，研究了T型分流三通这一重要管件对压缩机管网内部气流脉动的影响，建立了包含T型分流三通的管路气流脉动传递矩阵。运用CFX进行流体动力学仿真，通过分析管路内的压力分布与流场分布，研究了分流三通主干管路与分支管路直径比的变化对管路内气流脉动的影响。

往复压缩机 气流脉动 T型三通 直径比 CFX

大型往复压缩机广泛应用于石油、化工、冶金及能源等领域，作为压缩、输送气体的关键设备，在工业生产中有着不可替代的作用，其中压缩机的管道系统是保证物料稳定传输的关键部分。由于往复压缩机间歇性吸、排气的工作特点，使管道内形成压力和速度呈周期性变化的气流脉动，成为激发机组与管道振动的主要原因。当脉动的气流通过弯头、阀门、异径管及三通等管路元件时，产生的激振力使管网强烈振动。强烈的管道振动为生产现场埋下巨大的安全隐患，轻则影响经济效益，重则导致安全事故，严重威胁工作人员的生命安全[1]。

因此，深入研究往复压缩机管网内气流脉动的复杂机理与传递特性对于管道减振、安全生产及节约能源等方面具有重要意义，一直备受国内外学者关注。早在20世纪50年代，美国与苏联科学家就开始对气流脉动与管道振动进行理论推导与实验研究，提出了相关的理论模型和管道机械振动计算方法[2～4]。我国学者在20世纪70年代中期也开始对气流脉动与管道振动进行理论研究，结合工程案例，在生产实际中取得了较丰富的成果[5～7]。近年来，有限元模型的发展和计算机处理能力的日益强大，使得各类商用计算流体力学的模拟仿真软件功能日趋完善，为研究人员提供了新思路与新方法，提高了研究效率，对气流脉动抑制与消减管路振动、优化管路设计等方面起到了推动作用[8～11]。

在生产实际中，T型三通是一种在管道系统中用于流体连接、分流、汇总的典型管路结构，具有广泛的应用。笔者针对这一重要管道元件，建立了包含T型分流三通的管路气流脉动传递矩阵，通过进行CFX流体动力学仿真分析，研究了T型分流三通主干管路与分支管路管径比对管道内气流脉动的影响规律。笔者为往复压缩机管路设计和抑制复杂管网的气流脉动提供了理论参考。

1 往复压缩机管路中T型分流三通的气流脉动机理研究

1.1 气流脉动基本理论

平面波动理论是分析往复压缩机管道内气流脉动的基础理论之一，该理论用于描述波在平面内传播时的波动现象。由于压缩机输气管道的管径与管长之比非常小，可将管道内的流体流动视为一维非定常流动[6]。因此，用平面波动理论线性化方程，简化了压力脉动的分析过程。

在平面波动理论中，通过连续方程和运动微分方程的求解可以得到脉动压力pt的常系数偏微分方程：

(1)

在大型往复压缩机实际工况下，平均气流速度u0一般远小于气体的声速a，因此可以假设u0=0，则式(1)可简化为：

(2)

式(2)为基于往复压缩机气流特点的声学波动方程。该方程是后续计算推导的基础方程，其复数解为[6]：

(3)

式中A*、B*——复数常数；

n——压缩机转速；

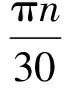
在工程实际中，包含T型三通的管路系统具有广泛的应用。通过运用上述平面波动理论的基本声学波动方程，对等截面直管和T型分流三通的气流脉动进行数学模型推导和动力学仿真分析，这对有效抑制管网内的气流脉动具有重要意义。

1.2 等截面直管气流脉动数学模型

(4)

ρ0——气体介质的平均密度。

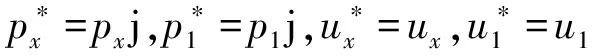
px=p1coskx-ρ0au1sinkx

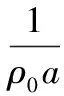
(5)

将式(5)写成矩阵形式，即：

(6)

其中，Mp称为等截面直管上下游距离x之间脉动压力和脉动速度的传递矩阵。

1.3 包含T型分流三通的管路气流脉动数学模型

T型三通在管路系统中可以起到流体连接、改变流体走向等作用，是具有广泛应用的典型管路结构。图1为包含分流T型三通的管路模型，由等截面直管单元a、T型分流三通单元b和等截面直管单元c3部分组成，其中，粗管表示主干管路，细管表示分支管路，管路中流体流向如图1中箭头所示。

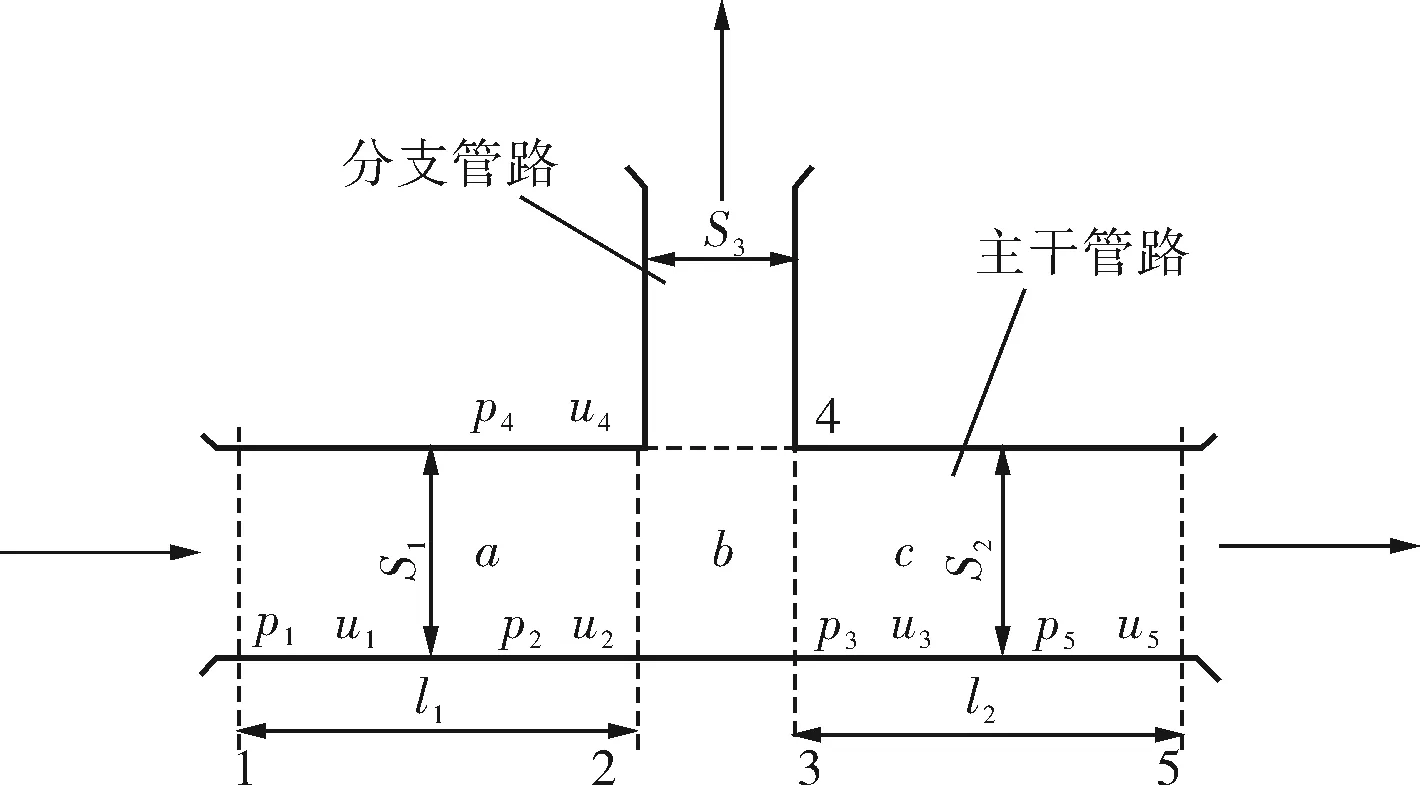
图1 包含T型分流三通的管路模型

由式(6)可得等截面直管单元a的传递矩阵Mp1和等截面直管单元c的传递矩阵Mp2：

(7)

下面推导T型分流三通单元b的气流脉动传递矩阵。截面2、3、4为紧靠分流T型三通的3个截面，由连续方程可以得到[6]：

p3=p2=p4

(8)

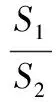
(9)

所以，T型分流三通的传递矩阵MJ为：

(10)

式(10)为考虑了分支管路的沿主干管路从截面2向截面3的T型分流三通传递矩阵。因此，可以得到管系末端脉动压力振幅p5和脉动速度振幅u5为：

(11)

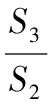
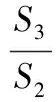
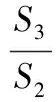
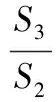
式中M——包含T型分流三通的管路传递矩阵。

从包含T型分流三通的管路传递矩阵M可知，三通主干管路与分支管路的管径比是影响管道内脉动压力振幅的重要参数之一，下文即通过流体动力学仿真对这一参数进行分析，研究T型分流三通对管路气流脉动产生的影响。

2 基于CFX的流体动力学仿真与分析

2.1 建立包含T型分流三通的管路有限元模型

笔者通过改变T型分流三通主干管路与分支管路管径比d1/d2这一参数，运用基于有限体积法与k-ε湍流模型的CFX流体动力学仿真，对管路内的压力分布与流场分布进行分析，研究T型分流三通对管路内气流脉动的影响。T型分流三通具体的有限元仿真模型如图2所示，参数见表1。

图2 包含T型分流三通的管路有限元

项目三通主干管路直径d1/m三通分支管路直径d2/m三通前入射管路长度L1/m三通后主分流管长度L2/m三通后支分流管长度L3/md1/d2模型10．1570．1571515151．0模型20．1570．1301515151．2模型30．1570．1041515151．5模型40．1570．0801515151．9模型50．1570．0671515152．3

2.2 求解设置

计算域内为理想状态下的可压缩空气，初始温度为60℃，粘度为2.01Pa·s，密度为1.06kg/m3。管道模型的入口边界条件设置为往复压缩机排气口的质量流率，其大小随时间变化，函数表达式为m=0.211|sin(10πt+5)|，单位为kg/s。主分流管与支分流管的出口条件出口1与出口2均为0.1MPa。仿真计算采用k-ε湍流模型，结合壁面函数理论，对计算域内的流体进行瞬态数值求解。

2.3 T型分流三通对管路内气流脉动影响规律的分析

求解运算完成后，对上述5组模型的计算结果进行数据处理。每组模型的主干管路部分为从入口到出口1的30m管路，由入射管路L1与主分流管L2两部分组成。5组模型均以入口为起点，每隔1m提取一组该模型主干管路yz横截面上压力随时间的变化值，得到脉动压力的时域数据。然后，再提取每组时域数据的峰峰值，得到5组T型分流三通主干管路内脉动压力峰峰值随管长的变化趋势对比图，如图3所示。

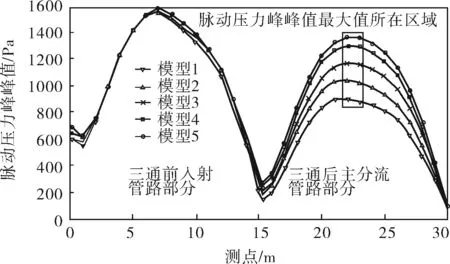
图3 T型分流三通主干管路内脉动压力峰峰值分布图

5组模型的分支管路为从入口到出口2的30m管路，由入射管路与支分流管两部分组成。对每组模型分支管路的数据提取与处理与相应的主干管路相同，从而得到了如图4所示的T型分流三通分支管路内脉动压力峰峰值随管长的变化趋势对比图。

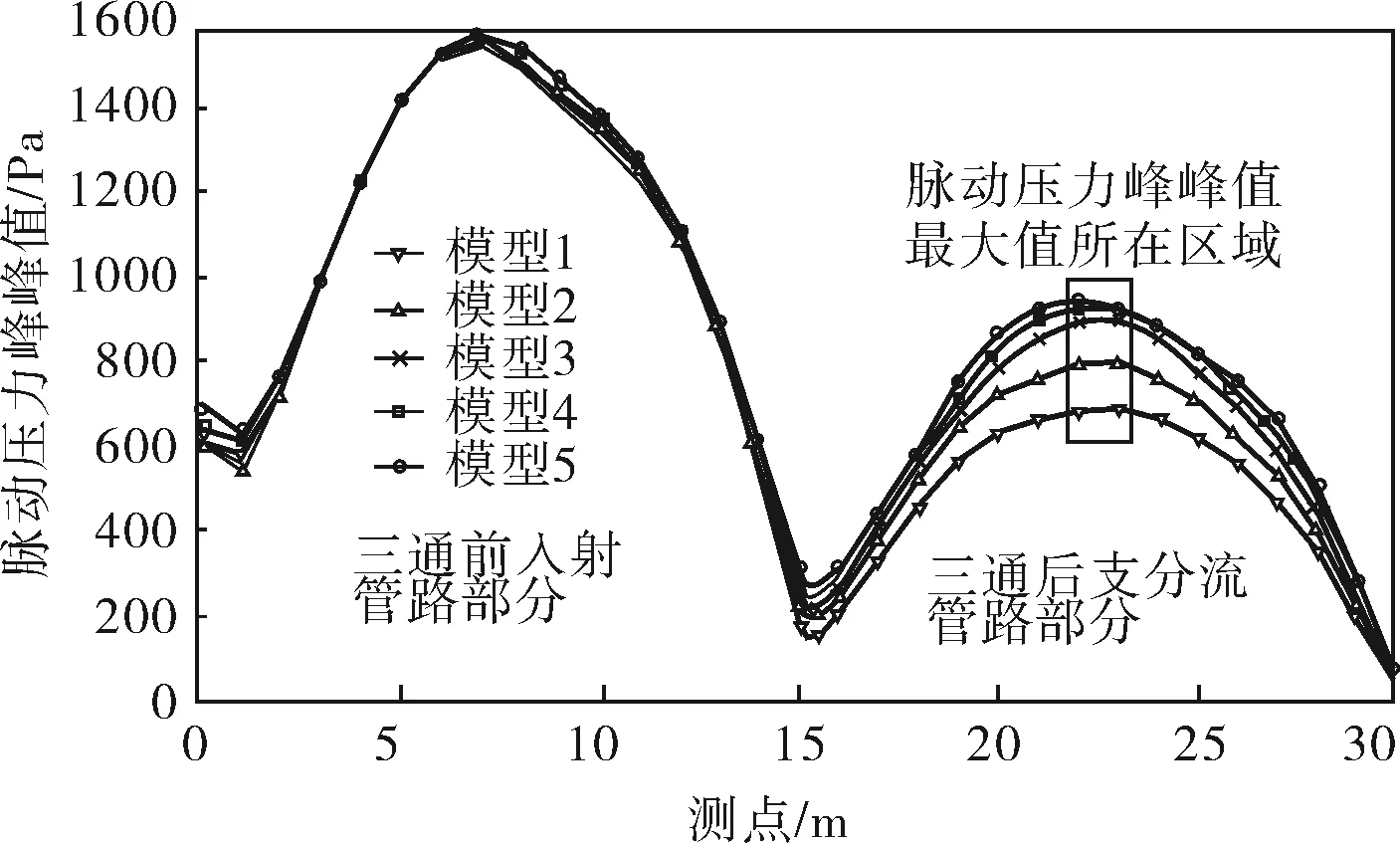
图4 T型分流三通分支管路内脉动压力峰峰值分布图

综合分析图3、4可以得到T型分流三通对管路内气流脉动的影响规律如下：首先，在三通前的入射管路中，5组模型脉动压力峰峰值近似相等，在三通后的两个分流管路中，脉动压力峰峰值产生了较大变化，可见T型分流三通对入射管路的影响很小，主要对三通后管路内的气流脉动产生较大作用；其次，由于三通的分流作用，在三通后的主分流管与支分流管中，气流脉动脉动压力峰峰值均小于三通前，同时，主分流管内的脉动压力峰峰值整体高于支分流管。最后，三通后各组模型脉动压力峰峰值随着管径比d1/d2的变化呈现出一定规律，分别提取图3、4中位于矩形区域内的T性分流三通后脉动压力峰峰值最大值，绘制出它随管径比变化的趋势(图5、6)，从图中可以看出，随着管径比d1/d2的增大，两分流管内脉动压力峰峰值最大值逐渐增大，并且在d1/d2<1.5时，增大管径比d1/d2对两分流管路内脉动压力峰峰值的增大作用更显著，当d1/d2>1.5时，两分流管路内脉动压力峰峰值最大值的增大幅度逐渐下降，趋于平缓。

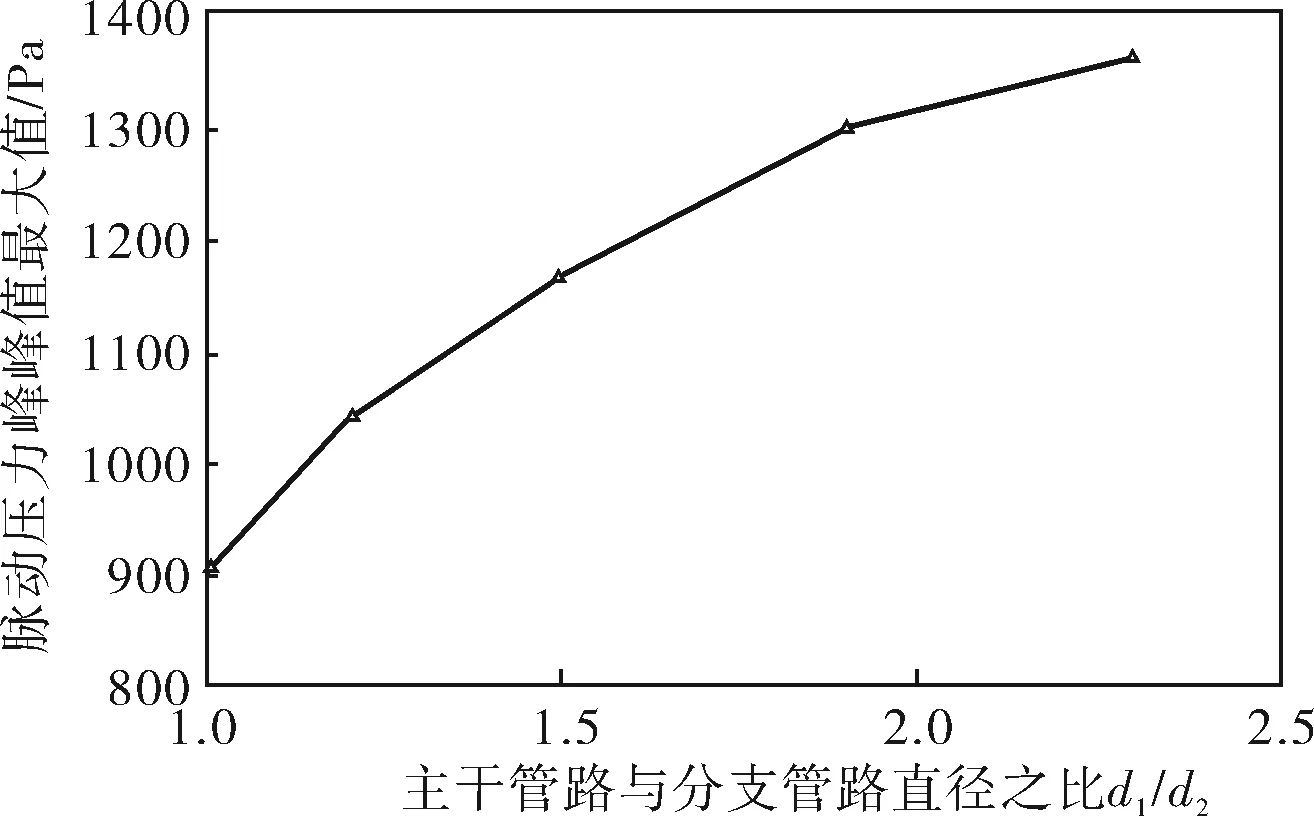
图5 主分流管内脉动压力峰峰值最大值 随d1/d2变化的趋势

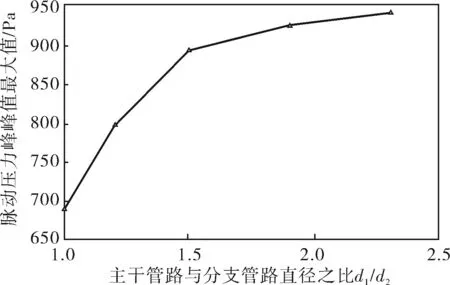
图6 支分流管内脉动压力峰峰值最大值 随d1/d2变化的趋势

图7为5组模型T型分流三通处的速度云图，可以看出，由于主干管道上存在分支管路，使得主干管路气流脉动一部分会在三通处形成透射波与反射波，沿着主干管线继续传播，同时另一部分则改变方向，成为分支管路的入射波，管路结构的突然改变使得流体湍流程度加剧，在三通颈处形成速度较大的湍流漩涡，流体的压力势能转化为湍流动能，使得T型分流三通后的脉动压力振幅减小。当d1/d2=1时，三通颈处的湍流程度最剧烈，使得该管径比下三通后管路内脉动压力峰峰值最小。而随着主干管路与分支管路管径比d1/d2的增加，三通颈处的湍流程度逐渐减弱，从而形成了如图3～6所示的管路脉动压力分布规律。

a. d1/d2=1.0

b. d1/d2=1.2

c. d1/d2=1.5

d. d1/d2=1.9

e. d1/d2=2.3

3 结论

3.1 笔者以平面波动理论为基础，建立了包含T型分流三通的管路传递矩阵，为描述T型分流三通对管网内气流脉动的影响提供了理论依据。

3.2 通过CFX流体动力学仿真，对管路内压力分布与流场分布进行分析发现，T型分流三通对三通后的主分流管与支分流管中的气流脉动均有较大影响，主分流管路内的脉动压力峰峰值整体高于支分流管路，并且，随着主干管路与分支管路管径比d1/d2的增加，两个分流管路内的脉动压力峰峰值也增大，气流脉动越剧烈。这是由于T型三通处管路结构的突然改变，使得三通处的湍流程度加剧，压力势能转化为湍流动能，当d1/d2增大时，湍流程度逐渐减小，使得三通后管路内脉动压力峰峰值随着d1/d2的增大而增大。

3.3 T型分流三通管径比对管路内气流脉动的影响规律为管路的优化设计提供指导作用，在工程实际中，可以结合这一规律，综合考虑现场情况，有效抑制管网的气流脉动。

3.4 在运用CFX进行流体动力学仿真时，将管道内壁设置为光滑，但在实际情况下，由于不能完全忽略管内流体的流动阻力，使这种简化对计算精度在可接受范围内造成一定影响。

3.5 在研究管路气流脉动影响规律时，若无前人经验或因条件所限无法进行实验时，可根据实际情况建立有限元模型进行CFD流体动力学仿真，根据仿真结果总结气流脉动规律，寻找消减气流脉动的方法。

[1] 樊力可.往复压缩机出口管系的振动分析及消振措施[D].上海：华东理工大学，2013.

[2] Edward N H，著，邵定山，译.气体压力波动问题南方气体协会的研究及其成果[J].Oil and Gas Journal，1958，56(19)：115～122.

[3] Watson W D.Vibration Analysis Key to Compressor Foundation Maintenance[M].United States：Oil and Gas Journal，1988：4.

[4] Maelaern J F T，Tramschek A B，Sanjines A，et al.A Comparion of Numerical Solution of the Unsteady Flow Equation Applied to Reciprocating Compressor[J]. Journal of Mechanical Engineering Science，1975，17(5)：67～73.

[5] 党锡淇，陈守五.活塞式压缩机气流脉动与管道振动[M].西安：西安交通大学出版社，1984：7～143.

[6] 谭平.天然气管线压力脉动激振分析[J].天然气工业，2005，25(9)：107～109.

[7] 党锡淇，陈守五，夏永源.孔板消减气流脉动机理的分析[J].西安交通大学学报，1979，13(2)：49～59.

[8] 张道刚，王茂廷，王杰，等. 往复式压缩机管道振动的ANSYS分析[J]. 化工设备与管道，2009，46(1)：55～57.

[9] 丁珏，翁培奋.90℃弯管内流动的理论模型及流动特性的数值研究[J].计算力学学报，2004，21(3)：314～321.

[10] 卜琳，李会雄，王海军，等.斜向三通管内射流混合特性的三维数值模拟[J].核动力工程，2008，29(5)：124～128.

[11] 韩文龙，韩省亮，白长青.往复压缩机管道系统气流脉动的数值与实验研究[J].西安交通大学学报，2013，47(5)：61～66.

ResearchonDynamicCharacteristicsofGasPulsationinTeeJunctionofReciprocatingCompressorPipingSystem

LIU Li-si, ZHANG Yang, FU Yu-dong, YANG Guo-an

(CollegeofMechanicalandElectricalEngineering,BeijingUniversityofChemicalTechnology)

The gas pulsation caused by intermittent operation of reciprocation compressor severely affects stable operation of the compressor and it is the main reason of the piping vibration. Based on the plane wave theory, the tee junction’s effect on the gas pulsation within compressor’s pipe network was discussed and the transfer matrix of the air pulsation in the pipeline’s tee junction was established. Through making use of CFX to do the computational fluid dynamics simulation and analyzing both pressure distribution and flow field distribution within the pipeline, the influence from the change of diameter ratio of tee junction’s main pipeline and branch pipeline on the gas pulsation within the pipeline was discussed.

reciprocating compressor, gas pulsation, tee junction, diameter ratio, CFX

国家重点基础研究发展计划(“973”计划，2012CB026004)。

刘丽思(1991-)，硕士研究生，从事机械设备故障诊断的研究。

联系人杨国安(1963-)，教授，从事机械设备故障诊断的研究，ygapublic@163.com。

TQ051.21

A

0254-6094(2017)01-0073-06

2016-03-01，

2016-11-02)