基于薄壁环压缩的铝合金管材应力−应变行为
李轩颖,徐雪峰,王 继,戴龙飞
基于薄壁环压缩的铝合金管材应力−应变行为
李轩颖,徐雪峰,王 继,戴龙飞
(南昌航空大学航空制造工程学院,南昌 330063)
采用环压缩实验研究LF2M铝合金薄壁管材在应变速率为0.1~1 s−1,成形温度为350~475 ℃条件下的应力−应变行为。提出一种薄壁环压缩的方法,得到薄壁管材热压下的变形行为。结果表明:环压缩试样的高度选择需要避免压缩过程中出现起皱缺陷。试样高厚比为1时,随着压缩量增加,切向压应力超过临界值引起起皱失稳;试样高厚比为3时,随着压缩量增加,压应力超过临界值,出现起皱现象;试样的高厚比为2时,压缩后试样无起皱缺陷。因此,壁厚为1 mm时,环压缩试样的最佳高度为2 mm。LF2M铝合金薄壁管材热变形过程中的流变应力可用双曲正弦本构关系来描述,平均激活能为160.67 kJ/mol。
LF2M铝合金;薄壁环;热压缩;高厚比;本构关系
管材的塑性加工是对管材的二次加工,属于管材的深加工范畴。管材被加工成为各种不同的组件,常用于军事领域(如军用飞机)和民用领域(如地下水管或建筑)[1−4]。无论管材在何处使用,研究其力学性能不仅是为了制造出成形质量好的零件,而且更有助于预测其寿命[5]。铝合金管材一般通过热挤压相应棒料而成,经过受热变形后材料的组织会发生动态回复和动态再结晶。因此,成形后管材性能将不同于初始棒料,故研究管材的热成形性能,不能直接选用其初始棒料的热成形性能,更不能选用对应的板料热成形性能,需要研究新的管材热压成形性能的测试方法,从而建立正确可靠的流变力学模型。
国内外研究者采用不同的方法测试管材性能构建材料本构模型。SANJARI等[6]设计一套主要用于管件塑性各向异性研究装置,采用自由收缩的自然胀形测试方法得到管材的成形性能。ZHAN等[7]采用国标GB/T 228—2002中的规定,对TA18钛合金直接进行单向拉伸试验,构建材料幂指数本构方程,用于指导钛合金管材的弯曲模拟与试验。邱小波等[8]通过测量鼓胀试验中管材的壁厚、胀形高度以及内部压力等通过参数并将其代入分析模型,得到管材的性能指标。HASHEMI等[9]依据美国标准,对直径小于25 mm的管材直接截取一段进行不同温度的单向拉伸试验,测得材料不同温度下的应力应变曲线,得到材料力学性能。ZAREI等[10]研究了薄壁管材受挤压变形情况,采用了管材母材板料试样进行单向拉伸试验,构建材料本构方程。
李峰等[11]利用有限元方法对不同圆环压缩过程中的分流行为进行模拟研究,揭示铝合金圆环压缩过程中分流行为的产生机理。王冠等[12]以6063铝合金薄壁梁结构为研究对象,对铝合金薄壁梁压缩变形研究诱导孔对变形行为与吸能性能的影响规律。李峰 等[13]采用有限元模拟及试验,对7075铝合金方环厚壁件压缩过程进行分析,研究工艺条件对方环件压缩变形流动行为的影响规律。通过对空心件轴向压缩方法获得材料变形行为有一定研究。但并未通过薄壁环压缩方法得到材料的应力−应变行为,同时,薄壁环的高度与厚度关系还有待研究。
从目前的文献报道看,国内外研究主要集中在利用液压胀形测试管材性能与构建材料本构模型;利用管材上的截取试样进行单向拉伸试验,测试管材的性能与构建材料的本构模型,利用管材母材为棒料或板料进行单向压缩或拉伸试验,测试母材的性能与构建材料的本构模型。对于反映管材热压下的性能测试方法,还未见报道,因此还需要研究新的管材热压成形性能测试方法,从而建立正确可靠的力学模型。本文作者提出一种从薄壁铝合金管材上直接截取管段进行热压缩试验,获得管材的应力−应变曲线,建立管材热压下的材料本构模型,将材料本构模型运用于薄壁管材缩口热挤压增厚变形,分析变形过程中的材料流变行为。
1 实验
本实验采用直径为22 mm,壁厚为1 mm的LF2M铝合金管材,截取高度为1、2和3 mm的环状试样,进行不同温度不同应变速率下的热压缩试验。加热温度分别为350、400、450和475 ℃,应变速率分别为0.01、0.1和1 s−1,总压缩变形量为60%,每一变形条件进行3次试验,计算其真实应力−应变值时取3种试验值的平均值,以保证试验结果的准确性。环状压缩试样需要保证两端面的平行度,以免偏心受力。设计专用模具(见图1)在热环境通用板材热成形试验机上进行试验(见图2),并设计专用定位板,以保证试样在模具中心受力(见图3)。定位板的外径与凹模相同,中间为直径为22 mm的孔,对半切开。定位环状试样时,将环状试样卡在定位板中间孔内,定位板的外径与凹模对齐,确定环状试样在凹模中心位置后,将两块定位板两侧轻轻取出,避免影响环状试样定位。

图1 压缩模具
试验机的压头在试样上时,只能沿轴向运动,不允许有其他自由度的移动和转动。为了减少试样与压头之间的摩擦,压缩试样通过砂纸磨去线切割划痕,并保证试样高度(见图4),在压缩过程中,将压缩表面均匀涂抹润滑剂(石墨)。压缩试验结束后立即对试样进行水淬以保留高温变形组织。根据试验结果获得数据,得到材料的应力应变曲线,分析材料的流变力学行为,建立可靠的材料力学模型。

图2 热环境试验机

图3 定位板

图4 环状压缩试样
2 结果与分析
2.1 环压缩试样高度分析
直接从管材截取环状试样进行热压缩试验,研究管材在热压下的材料流变应力。试样在压缩过程中,难免微弯,且力难免有偏心,容易造成试样除了单向压缩力外还有弯曲的影响。这两种受力状态同时存在时,压缩试验要得到的单向的应力均匀分布的单向试验结果,需要从试验技术上做大量工作,并给以一定限制条件。要避免压缩失稳,需要充分研究失稳极限,最重要的是需要保证压缩试样不宜过长,以避免在试样达到实验目的之前试样失稳[14]。
采用圆柱体进行高温压缩试验时,试样高度一般取=(1.5~2);采用环状试样测量摩擦因数的,环状试样的几何尺寸为外径:内径:高度=6:3:2。分析从圆柱体试样到厚壁圆环试样的几何尺寸标准,圆环试样高度()与厚度()的比值(/)为0.75~1,而厚壁圆环试样高度与厚度的比值约为1.33。可以得出,随着壁厚的减小,高度与厚度的比值随之增大。薄壁环状试样的几何尺寸并没有固定的标准,只有通过理论与实践的结合探索研究。
2.1.1 理论分析
金属塑性变形过程中,当材料所受载荷达到某一临界值后即使载荷下降,塑性变形还会继续,这种现象称为塑性失稳。失稳有压缩失稳和拉伸失稳。压缩失稳主要影响因素是刚度参数,它在塑性成形中主要表现为坯料的弯曲和起皱,在弹性或塑性范围内都可能发生[15]。
在弹性状态时,当压力达到某临界力K时,环状试样就产生失稳而弯曲。得到如下失稳准则:
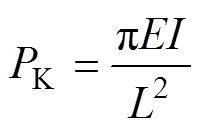
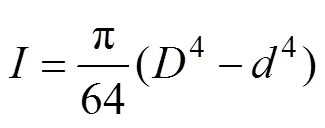
式中:为材料的弹性模量;为圆环的惯性矩;为圆环试样外径;为圆环试样内径。
当坯料内部的压应力超过屈服强度时,材料进入塑性状态,式(1)就不在适用了。塑性状态下的临界力为:
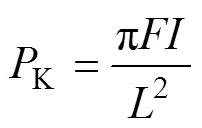
式中:F为切线模量。
对于外径为,内径为的矩形截面圆环试样,将式(2)代入式(3)可得临界压力:
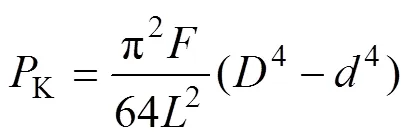
临界压应力:
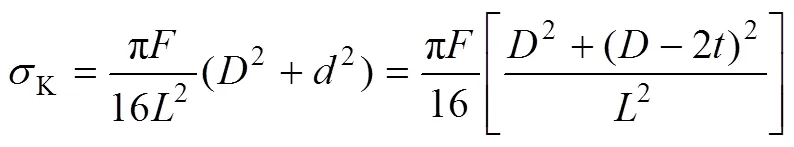
由得到的塑性压缩失稳的临界压力和临界压应力公式(4)与式(5)可以看出材料的抗压缩失稳能力除与材料的刚度性能参数有关外,还与受载的环状试样的几何参数(、、、)有着密切关系。本文作者提出一个高厚比的概念,即环状试样高度与厚度之比(/),衡量薄壁环状热压缩试样的尺寸标准。
在确定了环状试样的、、之后,当环状试样高厚比增大,试样高度增大,临界压力和临界压应力减小,即环状试样高度越高,越容易发生失稳,环状试样的压缩失稳往往表现为起皱失稳。
当切向压应力超过临界值时,同样会引起起皱失稳,通过力平衡法求得塑性失稳的临界应力:
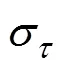
由式(6)可以看出,切向压应力的临界值与材料的折减弹性模量0、/有关。材料的弹性模量E、硬化模量越大,/越大,切向压应力的临界值越大,则出现压缩力引起的失稳可能性就越小。
通过式(5)和式(6)可以得知,环状试样的高厚比太大或太小均会随着压缩量的增加,出现起皱失稳。
2.1.2 实验分析
在实际试验中,环状试样在受压缩时,其失稳弯曲影响坯料的极限尺寸比例和成形极限(极限变形程度)。因此为了避免起皱失稳,本实验选择环状试样高厚比为1、2和3,即壁厚为1 mm时,试样高度为1、2和3 mm时,进行热压缩试验。
图6所示为高度为1、2和3 mm,在350 ℃,应变速率为0.01 s−1时,压缩后试样。在相同条件下,3个试样状态均与图中相似或相同,则呈现此状态无偶然情况。

图6 压缩后环状试样
根据式(5),当为3 mm时即高厚比为3时,临界压力和临界压应力值小与高厚比为1或2时,随着压缩量增大,材料发生堆积,压应力大于临界压应力时,压缩后试样应比高厚比为1或2时更容易出现压缩力引起的起皱失稳。试验结果表明,在/为3时,压缩后环状试样内部出现起皱现象。
根据式(6),当/为1时,相比于/为2或3时,/为1临界切向压应力较小,随着压缩量的增加,易出现因切向压应力值超过临界值的起皱失稳。观察/为1时,压缩后环状试样出现起皱现象。这是由于随着压缩量的增加,试样逐渐变薄,切向压应力逐渐增大,当切向压应力达到临界值时,坯料将产生起皱失稳。在环状压缩试验中,=1 mm,=1 mm时,切向压应力临界值小,随着压缩量的增加,切向压应力超过切向压应临界值出现起皱失稳现象。
根据式(5)和式(6),当环状试样高厚比为2时,在压缩过程中切向压应力和压应力均比高厚比为1和3时,临界压应力和临界切向压应力均较大,则出现起皱失稳的可能性较小。同时观察试验结果,与理论相符合。
经过实验和理论结合,可以得出,当对壁厚为 1 mm的环热压缩试验时,环状试样的最佳高度为 2 mm。
2.2 环状热压缩流变应力
为了正确反映管材在热压下的流变应力行为,主要研究高厚比为2时材料的变形行为。根据塑性变形体积不变的原理,通过实验过程中得到的力−位移曲线根据式(7)和式(8)得到真实应力−应变曲线。
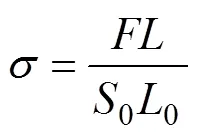
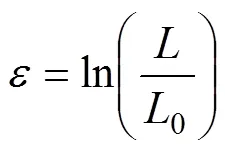
式中:为瞬时压力;0为试样原始面积;为试样瞬时高度;0为试样原始高度。
图7所示为LF2M铝合金薄壁环状试样在不同温度下压缩变形时的真应力−真应变曲线。由图7可见,热变形初期,流变应力随着变形程度的增大而升高,并快速达到某一峰值,随后随着应变量的增大,真应力不发生特别明显的变化,呈现稳态流变特征。在相同应变速率下,随着变形温度的升高,流变应力峰值明显降低。在同一变形温度下,随着应变速率的增加,流变应力峰值升高。说明LF2M铝合金管材具有正的应变速率敏感性。
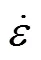
图7 不同温度环状试样热压缩变形真应力−应变曲线
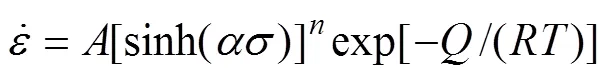
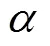
该式可以在整个应力范围内较好地描述金属材料常规热加工过程的流变应力变化规律,并广泛的用于估计各种金属及合金的热变形激活能。
在低、高应力水平下,流变应力与应变速率的关系分别可用指数关系和幂指数关系描述,即:
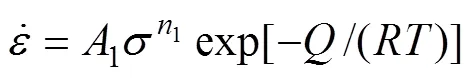
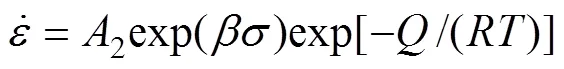

对式(9)~(11)两边取自然对数,然后通过整理,可统一表示为:
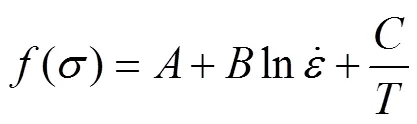
对式(10)和式(11)两边取对数,并进行整理,可得:
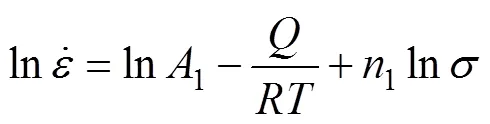
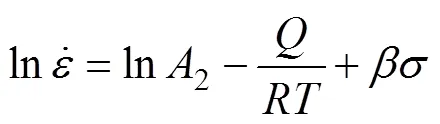
如果、和T之间的关系满足Arrhenius型方程,那么对于给定的应变,为和的双线性函数。图8所示为应变为0.35和0.3时,和的关系图。从图8可知,与和的双线性关系均较明显,则说明可以采用Arrhenius型方程描述LF2M铝合金薄壁管材热压下的流变应力行为。
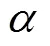
对式(9)两边取对数,并假定热变形激活能与温度无关,可以得到:
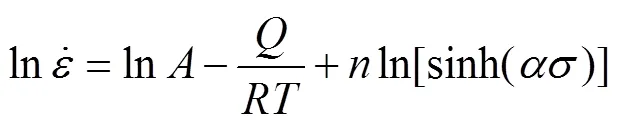
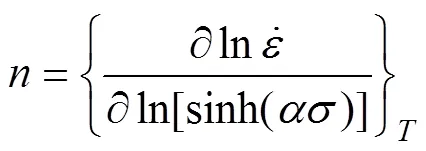
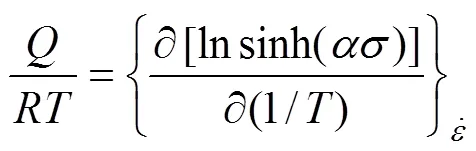
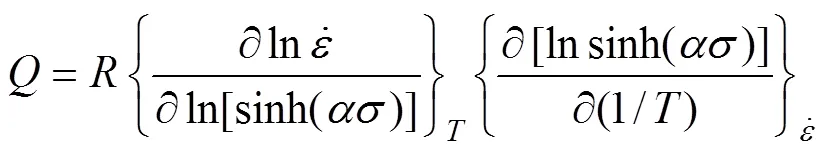
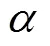
将、和的值代入,即可求得不同温度下的值,取其平均值,得=123990.228 s−1。则LF2M铝合金薄壁管材热压下材料常数如表1所列。
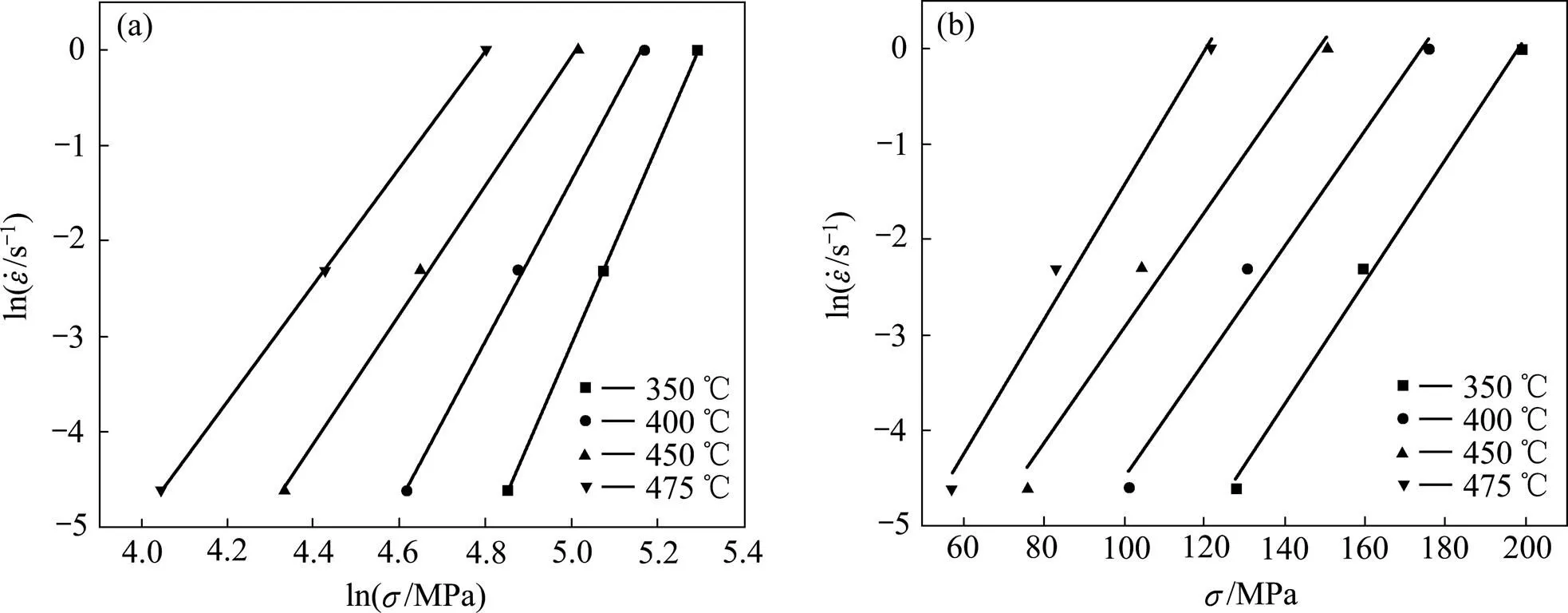
图9 应力与应变速率的关系
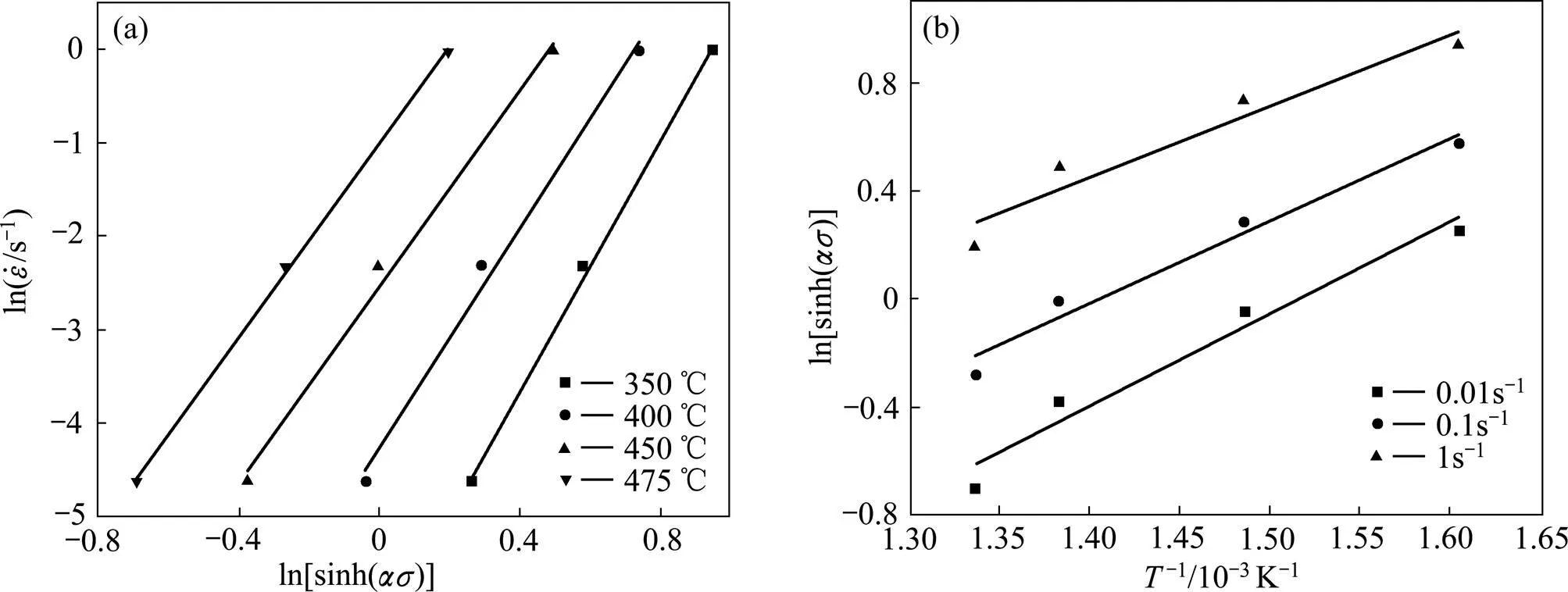
图10 和以及和1/T的关系

表1 LF2M铝合金薄壁管材热压下材料常数
3 结论
1) 从薄壁管上直接截取环状试样进行热压缩试验,可以得到管材在热压状态下的材料流变行为。
2) 环状试样的高度是能否准确描述管材热压状态下的材料流变行为的重要因素。当高厚比为1时,切向压应力超过临界值引起起皱失稳;当高厚比为1时,压应力超过临界值导致起皱失稳;当高厚比为2时,压缩后试样无起皱缺陷,能准确描述管材热压下的材料流变行为。因此,当环状压缩试样壁厚为1 mm时,试样最佳高度为2 mm。
3)在应变速率一定的条件下,合金的流变应力随变形温度的升高而减小;在变形温度一定的条件下,合金的流变应力随应变速率的增大而增大。
[1] JAHANBAKHSH A, HAGHGOU H R, ALIZADEH S. Experimental analysis of a heat pipe operated solar collector using water-ethanol solution as the working fluid[J]. Solar Energy, 2015, 118(4): 267−275.
[2] NAOUM-SAWAYA J, GHADDAR B, ARANDIA E, ECK B. Simulation-optimization approaches for water pump scheduling and pipe replacement problems[J]. European Journal of Operational Research, 2015, 246(1): 293−306.
[3] RYSSEL S T, ARVIN E, LÜTZHØFT H C, OLSSON M E, PROCHÁZKOVÁ Z, ALBRECHTSEN H J. Degradation of specific aromatic compounds migrating from PEX pipes into drinking water[J]. Water Research, 2015, 81: 269−278.
[4] YU W B, LIU W B, LAI Y M, CHEN L, YI X. Nonlinear analysis of coupled temperature-seepage problem of warm oil pipe in permafrost regions of Northeast China[J]. Applied Thermal Engineering, 2014, 70(1): 988−995.
[5] LIU Z, BAO Y W, WAN D T, HU C L, MA D L, TIAN Y. Investigation on two methods for evaluating mechanical properties of tube materials[J]. Journal of Inorganic Materials, 2016, 31(2): 213.
[6] SANJARI M, TAHERI A K, MOVAHEDI M R. An optimization method for radial forging process using ANN and Taguchi method[J]. The International Journal of Advanced Manufacturing Technology, 2009, 40(7): 776−784.
[7] ZHAN M, HUANG T, JIANG Z Q, ZHANG P P, YANG H. Determination of process parameters for the NC bending of a TA18 tube[J]. The International Journal of Advanced Manufacturing Technology, 2013, 68(1): 663−672.
[8] 邱小波, 高光藩, 曹学刚. 鼓胀试验在管材力学性能测试中的研究进展[J]. 石油化工设备, 2013(6): 60−63. QIU Xiao-bo, GAO Guang-fan, CAO Xue-gang. Research progress of bulge text in determining tubular material mechanical properties[J]. Petro-Chemical Equipment, 2013, 42(6): 60−63.
[9] HASHEMI S J, NAEINI H M, LIAGHAT G, TAFTI R A, RAHMANI F. Numerical and experimental investigation of temperature effect on thickness distribution in warm hydroforming of aluminum tubes[J]. Journal of Materials Engineering and Performance, 2013, 22(1): 57−63.
[10] ZAREI H, KRÖGER M, ALBERTSEN H. An experimental and numerical crashworthiness investigation of thermoplastic composite crash boxes[J]. Composite Structures, 2008, 85(3): 245−257.
[11] 李 峰, 初冠南, 刘晓晶. 铝合金圆环压缩过程中的分流行为[J]. 中国有色金属学报, 2009, 19(11): 1923−1927. LI Feng, CHU Guan-nan, LIU Xiao-jing. Diffluence behaviour of aluminium alloy during ring compression[J]. The Chinese Journal of Nonferrous Metals, 2009, 19(11): 1923−1927.
[12] 王 冠, 刘志文, 徐从昌, 李落星. 诱导孔对铝合金薄壁梁轴向压缩变形行为的影响[J]. 中国有色金属学报, 2016, 26(3): 494−506. WANG Guan, LIU Zhi-wen, XU Cong-chang, LI Luo-xing. Effect of cut-outs on axial collapse behaviors of aluminum with thin-walled structure[J]. The Chinese Journal of Nonferrous Metals. 2016, 26(3): 494−506.
[13] 李 峰, 徐永超, 李 超, 刘晓晶. 铝合金方环件压缩变形规律及机理[J]. 中国有色金属学报, 2011, 21(11): 2751−2756. LI Feng, XU Yong-chao, LI Chao, LIU Xiao-jin. Deformation rule and mechanism in compress process of aluminium alloy square ring[J]. The Chinese Journal of Nonferrous Metals. 2011, 21(11): 2751−2756.
[14] 沈超明, 杨绘峰, 汪雅琪. 一种高温条件下金属“规定非比例压缩强度”试验方法尝试[J]. 实验技术与管理, 2010, 27(6): 27−30. SHEN Chao-ming, YANG Hui-ming, WANG Ya-qi. An attempt to test “proof strength non-proportional compression” of mentals at high temperature[J]. Experimental Technology and Management, 2010, 27(6): 27−30.
[15] 俞汉清, 陈金德. 金属塑性成形原理[M]. 北京: 机械工业出版社, 1999. YU Han-qing, CHEN Jin-de. Principle of mental plastic forming[M]. Beijing: Machinery Industry Press, 1999.
[16] 李成侣, 潘清林, 刘晓艳, 何运斌, 李文斌. 2124铝合金的热压缩变形和加工图[J]. 材料工程, 2010, 2010(4): 10−14.LI Cheng-lu, PAN Qing-lin, LIU xiao-yan, HE Yun-bin, LI Wen-bin. Hot compression deformation and processing maps of 2124 aluminum alloy[J]. Journal of Materials Engineering, 2010, 2010(4): 10−14.
[17] 李慧中, 张新明, 陈明安, 周卓平. 2519铝合金热变形流变行为[J]. 中国有色金属学报, 2005, 15(4): 621−625. LI Hui-zhong, ZHANG Xin-ming, CHEN Ming-an, ZHOU Zhuo-ping. Hot deformation behavior of 2519 aluminum alloy[J]. The Chinese Journal of Nonferrous Metals, 2005, 15(4): 621−625.
[18] SELLARS C M, TEGART W J M. Hot workability[J]. International Materials Reviews, 1972, 17(1): 1−24.
[19] POIRIER J P. 晶体的高温塑性变形[M]. 大连理工大学出版社, 1989. POIRIER J P. Plasticite a haute temperatures des solides cristallinsp[M]. Dalian: Dalian University of Technology Press, 1989.
Stress−strain behavior of aluminum alloy pipe based on thin-walled ring compression
LI Xuan-ying, XU Xue-feng, WANG Ji, DAI Long-fei
(School of Aviation Manufacturing Engineering, Nanchang Hangkong University, Nanchang 330063, China)
The stress-strain behavior of LF2M aluminum alloy of thin-walled tube during hot compressing deformation was studied, under the conditions of strain rate range of 0.1−1 s−1, and the temperature range of 350−475 ℃. A method of thin-walled ring compression was proposed to obtain the deformation behavior of the thin-walled tube under hot extrusion. The results show that the height of the ring compression sample is selected to avoid wrinkling defects during the compression process. When the ratio of the height to thickness is 1, with the increase of the amount of compression, the tangent pressure exceeds the critical value caused to the wrinkling destabilization. When the ratio of the height to thickness is 3, the compression stress exceeds the critical value caused to the wrinkling destabilization with the increase of the amount of compression. When the ratio of the height to thickness is 2, the specimen have no wrinkling destabilization. Therefore, when the wall thickness is 1mm, the optimum height of the ring compression specimen is 2 mm. The flow behavior of LF2M aluminum alloy of thin-walled tube is described by the hyperbolic sine constitutive equation, and an activation energy of 160.67 kJ/mol is calculated.
LF2M aluminum alloy; thin-walled ring; hot compression; ratio of height to thickness; constitutive relation
(编辑 王 超)
Project(51405219) supported by the National Natural Science Foundation of China; Project (BA201306321) supported by Production Project of AVIC, China
2016-08-15;
2017-03-28
XU Xue-feng; Tel: +86-13627919899;E-mail: xfwinzy@163.com
10.19476/j.ysxb.1004.0609.2017.10.08
1004-0609(2017)-10-2020-09
TG146.2
A
国家自然科学基金资助项目(51405219);中航工业产学研项目资助(BA201306321)
2016-08-15;
2017-03-28
徐雪峰,副教授,博士;电话:13627919899;E-mail: xfwinzy@163.com

