基于大数据的震灾应急物资需求预测方法研究

石钰磊 成世杰 宋启杰

（62421部队，北京 100071）

基于大数据的震灾应急物资需求预测方法研究

石钰磊 成世杰 宋启杰

（62421部队，北京 100071）

地震发生后，抗震救灾指挥部门很难在第一时间获知灾区对应急物资的需求情况，不利于救援资源的合理调配部署。基于大数据理念，依靠已有的数据积累，采用粒子群优化径向基神经网络的机器学习方法，结合安全库存模型，构建了震灾应急物资需求预测模型。算例验证结果表明，该模型具有一定的实用性和有效性。

抗震救灾，大数据，应急物资，需求预测

我国是一个自然灾害频发的国家，尤其是地震灾害，严重危害着我国人民群众的生命和财产安全。震灾具有突发性、非常规性和不确定性等特点，在地震发生后，受灾区域的交通线路和通讯系统通常会被严重破坏，抗震救灾指挥部门很难在第一时间获知灾区群众对应急物资的需求情况，不利于救灾资源的合理部署及运输力量的规划调配。因此，研究一种能够在震灾发生后，第一时间较为准确预测出灾区应急物资需求的方法，对于规范应急物资采购、指导应急储备仓库建设，以及辅助应急救援指挥决策等均有重要的现实意义。

目前，虽然国内外学者对应急物资需求预测方法开展了大量研究，但都处于起步阶段，应用成果并不多见[1]。根据预测原理不同，可将现有应急物资需求预测模型分为案例推理模型（CBR）、数学算法拟合模型和分步式间接预测模型等三大类。现有的预测方法受到应急救援案例数据库不完善的限制，普适性不足，且受参数选择的影响较大，因此，在实际指导应急救援中，还主要依靠专家经验来判断受灾地区所需物资量。

“大数据”是近年来在全球范围内迅速兴起的一个新名词，其核心就是预测[2]。大数据的预测方式不是基于传统的因果关系进行推测，而是跳出传统因果关系的思维局限，通过对大量数据的搜集、挖掘和分析，发现数据间隐藏的相关关系，从而揭示事物发生和发展的内在规律，能够做出更快、更符合实际的预测。要想利用大数据来进行预测，一般需要经历数据采集、数据分析与挖掘、机器学习等3个步骤[3]。

本文基于大数据理念，依靠已有的数据积累，采用分步式预测法，即先利用径向基函数（Radial basis function，RBF）神经网络预测震灾伤亡人数，再利用安全库存理论构建动态库存模型来估算应急物资需求量。实验结果表明，该方法运算速度较快，并具有较好的预测精度。

1 震灾伤亡人数预测模型

1.1 数据准备

本文搜集了近几十年我国发生的大型地震中受灾较为严重的39个地区作为样本，包括：云南澜沧、耿马，四川汶川、雅安，青海玉树等，所选样本的地震震级均在6.0级以上。

在地震灾害发生初期，一般可迅速获得发生时间、地震震级、地震破坏烈度、发生地点的建筑抗震设防平均系数、当地的受灾人数、人口密度、地震有无事先预报等信息。因此，为在地震后第一时间对灾区伤亡人数进行预测，选取震级、地震破坏烈度、发生时间、抗震设防系数、受灾人数、人口密度、地震预报水平等7个可迅速获取的参数作为指标来进行分析，具体信息如表1所示。其中，设定较易发生人员伤亡的时间段凌晨0时至6时为2，其它时间段为1；设定地震预报水平分为3级：1级表示无预报，2级表示有预报但存在偏差，3级表示预报准确。

2.2 样本数据挖掘

主成分分析法是一种数学线性变换方法，旨在利用降维的思想，在引进多方变量的同时将复杂因素归结为几个主成分，使问题简单化，同时能够得到更加科学、有效的数据信息[4]。由于本文各样本数据相关性较高，因此，采用Matlab对样本集进行主成分分析处理。样本各主成分特征值、贡献率与累计贡献率如表2所示。

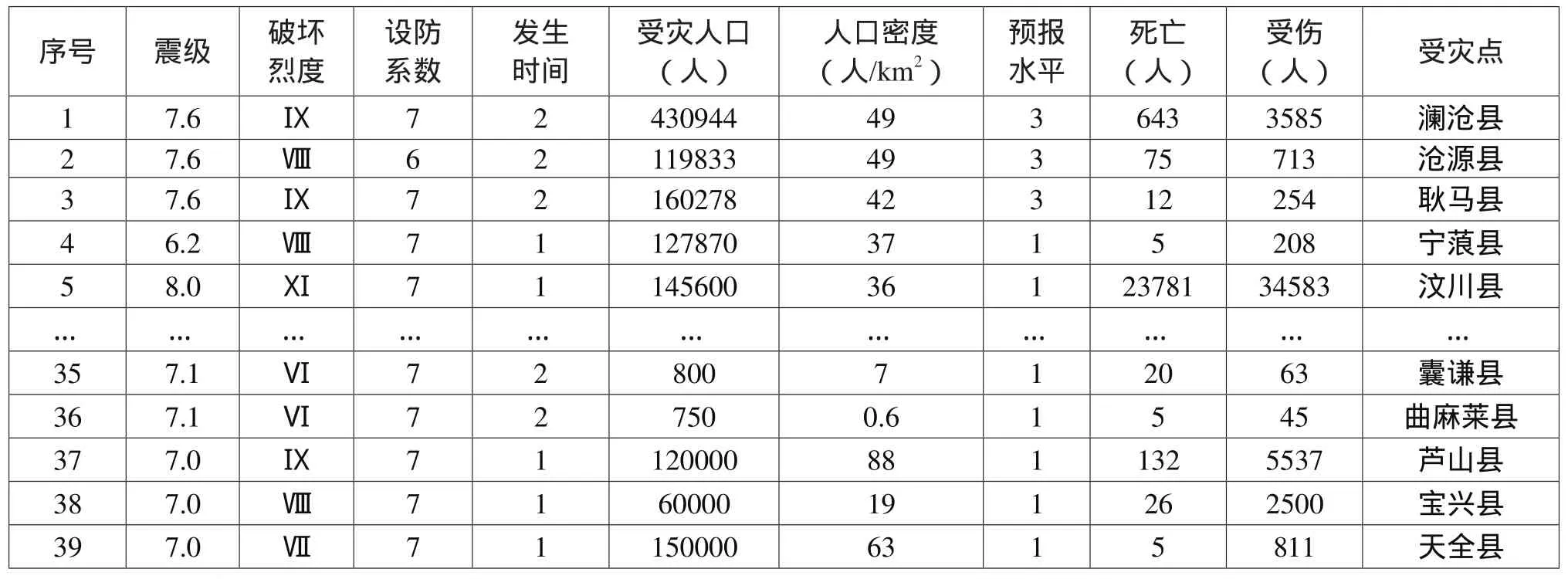
表1 地震灾害人员伤亡统计样本集

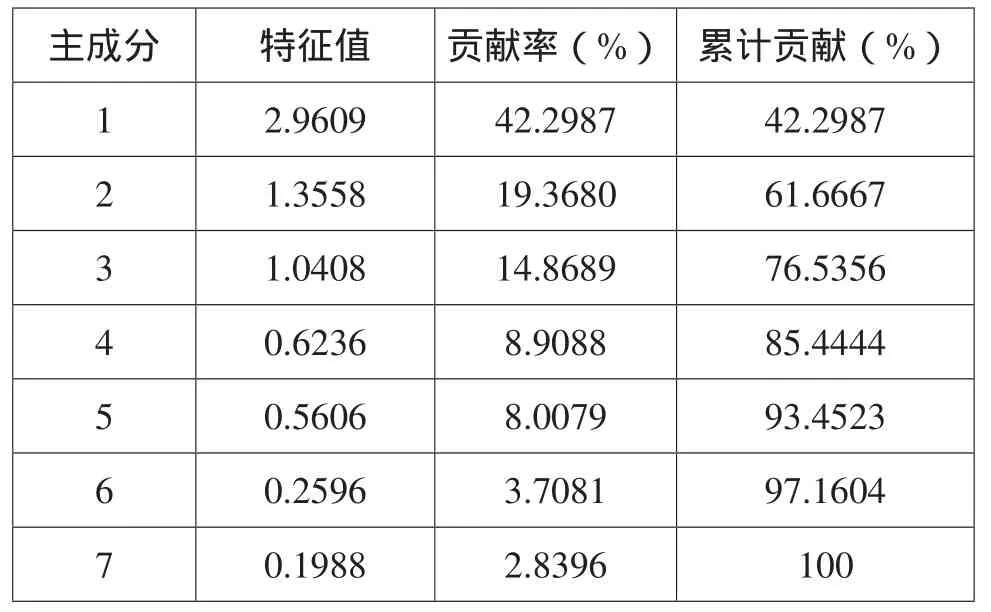
表2 样本各主成分的特征值、贡献率和累计贡献率

从表2可以看出，前5个主成分的累计贡献率为93.4523%，超过了90%，故本文选取这5个主成分替代原始的7个变量作为RBF神经网络的输入。

2.3 机器学习——改进型RBF神经网络预测模型

RBF神经网络是一种局部逼近网络，相比于其它神经网络，具有在相同精度要求下，学习速度快、不易陷入局部极小值等优点。随着大数据技术的发展，神经网络作为一种人工智能处理技术，与云计算相结合，正在实际应用中发挥着越来越大的作用。本文在结合前期研究成果的基础上[5]，采用收敛速度更快、预测准确度更高的基于粒子群（Particle swarm optimization，PSO）优化算法的RBF神经网络方法来预测震灾伤亡人数。使用PSO算法优化RBF神经网络的流程如图2所示。

2.4 伤亡人数预测

在进行神经网络学习之前，需要先对数据进行归一化处理，同时，为了使样本均匀分布，并保证学习的科学性，将样本原先的顺序打乱并随机抽取33组学习样本和6组验证样本，然后建立RBF神经网络模型。样本学习曲线图如图3所示。

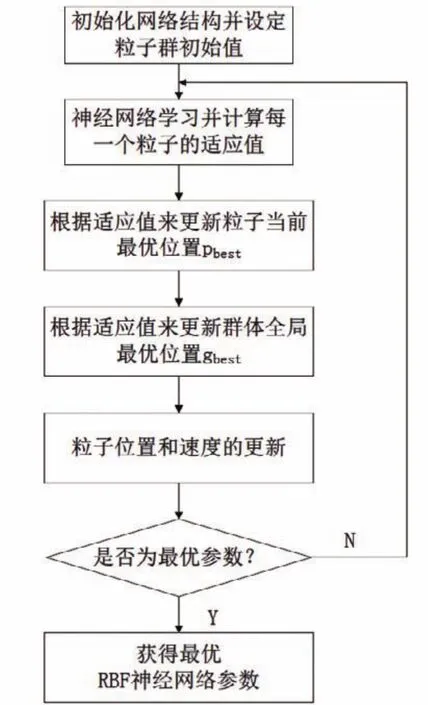
图2 PSO算法优化RBF神经网络流程图

从图3可以看出，经过PSO算法优化后的RBF神经网络在学习过程中收敛平稳、收敛速度快、偏差度低，且达到了要求精度。

对6组验证数据的前5个主成分进行仿真学习，经过反向标准化得到仿真输出值，如表4所示。

图3 神经网络样本学习曲线图

表4 验证样本神经网络仿真输出值

将其与实际值进行对比，如图4所示。可以看出，使用本文所建立的预测模型所得到的地震人员伤亡预测值与实际值有很好的拟合性，预测准确度较高。

图4 案例样本预测值与实际值对比图

3 应急物资需求量估算模型

地震发生后，向灾区供应物资时存在着很多的不确定性因素，例如，地理条件致使交通通道受堵，或者急需的某类物资库存不足等。同时，震灾的应急物资供给具有弱经济型，其首要目标是不惜一切代价救人。因此，为了提高预测质量，本文在估算受灾群众对某种物资的需求时，引入了商业物流中的安全库存概念，用以缓冲救援过程中的诸多不确定性因素。

3.1 估算模型构建

参考随机需求满足率和随机提前期下的安全库存模型，构建震灾应急物资需求估算模型。为充分满足灾区群众对应急物资的需求，这里将公式中的提前期即连续向灾区供给物资的时间间隔期取为其上限，标记为I。

其中，记地震发生时的时刻为0，由此开始以小时为单位计时，标记为t（t=0, 1, 2, …）；以m表示某种应急物资，如方便食品、御寒物资等。

式（1）中，P表示灾区人口总数，D（t）表示t时刻灾区的死亡人数，S（t）表示t时刻灾区的幸存者人数。

式（2）中，Qm（t）表示t时刻灾区所需物资m的数量；qm表示每位灾民单位时间对物资m的需求量；ә表示灾区所需物资的缺货率，则1-ә表示所需物资的满足率，Z1-ә表示服务水平系数，可通过正态分布表查询，本文中取其最大值；表示截止到t时刻，灾区对物资m每小时需求的标准差，可由公式（3）获得；Am（t）表示t时刻已经运抵灾区的物资m数量，Bm表示灾区内物资m的库存量。W（t）表示t时刻灾区的受伤人数。

式（4）表示物资需求量Qm（t）的平均值。

3.2 算例分析

利用文中构建的模型，对2014年8月3日16时30分发生在云南省昭通市鲁甸县的6.5级地震所需的应急物资量进行了预测。

第1步：收集案例数据

地震发生时，经测地震烈度达9度，地震在鲁甸县造成617人死亡，3143人受伤，其它指标数据如表5所示。

第2步：预测伤亡人数

利用文中学习的神经网络模型，输入表5中的参数进行预测，得到预测值为死亡人数587人，受伤人数2976人，与实际情况偏差很小。

表5 鲁甸县震后参数

表6 公式相关参数设置

第3步：估算各类应急物资需求量

对于灾区人民每人每日物资供应量，张培静已经在文献[6]中进行了统计分析、国务院也下发过相应标准。

本文选取能够保障基本生活条件的4种物资进行计算，分别是饮食类中的瓶装水、方便食品、御寒物资类的帐篷和药品中的抗生素，公式中相关参数设置如表6所示。

本文中的单位物资需求量设置的是需求平均值，实际操作中，可根据人员类别、天气条件、区域特征等不同情况具体设置；另外，本文中设置应急物资满足率为95%，提前期上限为6h，其目的在于最大限度满足灾区基本生活条件需要。

那么由公式（1）可得S（t）=434413（人）；

在地震发生初期，，则由公式（2）可得：

q1（0）=160×6×434413=417036480（ml）

q2（0）=50×6×434413=130323900（g）

q3（0）=0.25×434413»108604（顶）

q4（0）=80×6×2976=1428480（mg）

通过计算，地震发生后，抗震救灾指挥部门应在第一时间向灾区筹集调拨瓶装水约417036480ml，方便食品约130323900g，帐篷约108604顶，抗生素约1428480mg。

本文研究的方法旨在为抗震救灾指挥部门第一时间提供决策支持，在实际救灾过程中，随着救援人员进入灾区后，根据实时反馈回的实际信息，可对应急物资量进行动态调整。

4 结束语

由于地震灾害应急救援过程中的应急物资需求预测问题具有复杂的非线性变化规律，要建立精确的数学模型相当困难，因此，本文基于大数据的理念，将PSO-RBF神经网络预测模型引入该问题，并结合安全库存公式构建了应急物资需求预测模型，同时通过对云南鲁甸地震所需物资进行计算，验证了该模型的有效性，为震灾应急物资需求预测问题提供了一种解决方法。

1 林勇, 姜大立, 汪贻生, 等. 震灾应急物资动态需求预测模型研究[J]. 后勤工程学院学报, 2015, (3): 58～61

2 维克托·迈尔·舍恩伯格, 肯尼斯·库克耶. 大数据时代[M]. 杭州: 浙江人民出版社, 2012

3 IBM商业价值研究院. 分析: 大数据在现实世界中的应用[R]. IBM报告会, 2013

4 John A Rice. 数理统计与数据分析[M]. 田金芳, 译. 北京: 机械工业出版社, 2011

5 石钰磊, 贾斌, 董立峰, 等. 基于改进型RBF神经网络的震灾人员伤亡数预测方法研究[J]. 军事交通学院学报, 2015, 17(3): 91～95

6 张培静. 抗震救灾物资供应的适应性研究——以汶川地震救灾物资的供应为例[D]. 成都: 西南交通大学,2010

1009-8119（2017）10（1）-0058-04