基于流速幂级数解的明渠纵向离散系数计算方法

张文俊,胡 煜,任华堂,夏建新

(中央民族大学生命与环境科学学院,北京 100081)

基于流速幂级数解的明渠纵向离散系数计算方法

张文俊,胡 煜,任华堂,夏建新

(中央民族大学生命与环境科学学院,北京 100081)

针对纵向离散系数计算多直接采用经验公式或在流速分布的求解中引入经验公式,不能完全反映离散物理机制的问题,基于矩形断面一维水流控制方程,利用幂级数求解流速分布的理论解,提出了矩形断面明渠纵向离散系数的计算方法,并进一步将其推广至天然河流。利用该方法计算了104条天然河流的纵向离散系数,结果表明计算值与实测值处于同一量级,计算结果在可接受范围内。

纵向离散系数;明渠;幂级数;流速分布

近10年来,河流突发水污染恶性事件时有发生,不仅对河流水生生态系统造成严重破坏,更为严重的是对下游大中城市供水安全造成威胁,如2005年松花江特大突发苯污染事故、2010年福建紫金矿业铜酸水渗漏事故、2012年广西龙江镉污染事故等。如何模拟污染物云团在河流中的迁移过程,准确预测污染物到达各取水口时间以及恢复供水时间,是制定污染事故应急预案的基础。由于断面流速分布的不均匀性,排放到河流中污染物形成的云团形状将发生变化,即为河流的纵向离散作用。离散作用的强弱直接决定了污染云团迁移过程,在天然河流污染物预测中,由于计算量小、所需资料少等优点,多采用一维纵向迁移离散方程求解,将流速分布不均匀导致的离散作用概化为离散项,而离散项准确求解主要依赖于纵向离散系数,因此,准确确定纵向离散系数对于精准预测河流突发污染的影响范围和时间具有重要意义。

天然河流纵向离散系数为河流水环境模型的关键参数,一直是环境水力学研究中的热点问题。1954年Taylor[1]根据圆管试验基于径向扩散和纵向离散平衡首先提出了纵向离散系数的概念,Elder[2]将纵向离散系数的计算从圆管拓展到不考虑横向差异的明渠中,基于垂向扩散和纵向离散的平衡得到离散系数计算公式。对于天然河流,Fischer等[3]指出明渠纵向离散主要是由于纵向流速的横向分布不均匀引起的,而流速垂向差异的影响可忽略不计,并基于横向扩散和纵向离散的平衡推导出三重积分形式的纵向离散系数计算公式:

(1)

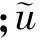
(2)

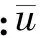
在天然河流中,由于流体运动的非线性特性,无法得到流速的分布资料。在离散系数的确定上,除了示踪试验[4]方法之外,仍然以经验公式为主,通过量纲分析等方法将离散系数表示为河流特征参数平均流速、底部摩阻流速、水深、河宽等变量的函数[5],通过对实测数据的拟合分析得到了一系列公式,如Seo等[6]、Kashefipour等[7]、Sahay等[8]的公式,但这些公式物理意义不明确,且主要是用于特定类型的河流,不易推广。

随着对河流水动力特性认识的不断深入,基于合理假定得到流速分布特性,使得利用式(1)计算河流纵向离散系数具备可行性。邓志强等[9]以抛物型断面河道为对象,基于谢才公式得到横断面流速分布,继而导出纵向离散系数理论公式;陈永灿等[10]基于最大熵值原理提出确定梯形断面纵向流速分布的方法,得到梯形断面明渠纵向离散系数计算公式; Wang 等[11]则通过矩形断面的水流控制方程,采用傅里叶级数形式表达的流速分布,求解得到纵向离散系数计算公式。

虽然相关方法在计算离散系数中都取得了一定的效果,但是在流速分布求解中均不同程度地引入了经验公式或数理原理等,而采用流体动力学方程进行流速求解再得到离散系数的公式尚不多见。本文以常见的矩形断面形态河流为对象,基于恒定均匀流条件下河流控制方程,采用幂级数形式求解得到河流流速分布,将流速分布代入式(1)求解可得矩形断面河流纵向离散系数值,并将其推广到天然河流纵向离散系数的计算。

1 纵向离散系数的幂级数求解方法

1.1 矩形断面流速分布的求解

对于图1所示的均匀恒定明渠流动,流速分布满足以下动力学方程:

(3)

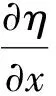
(4)

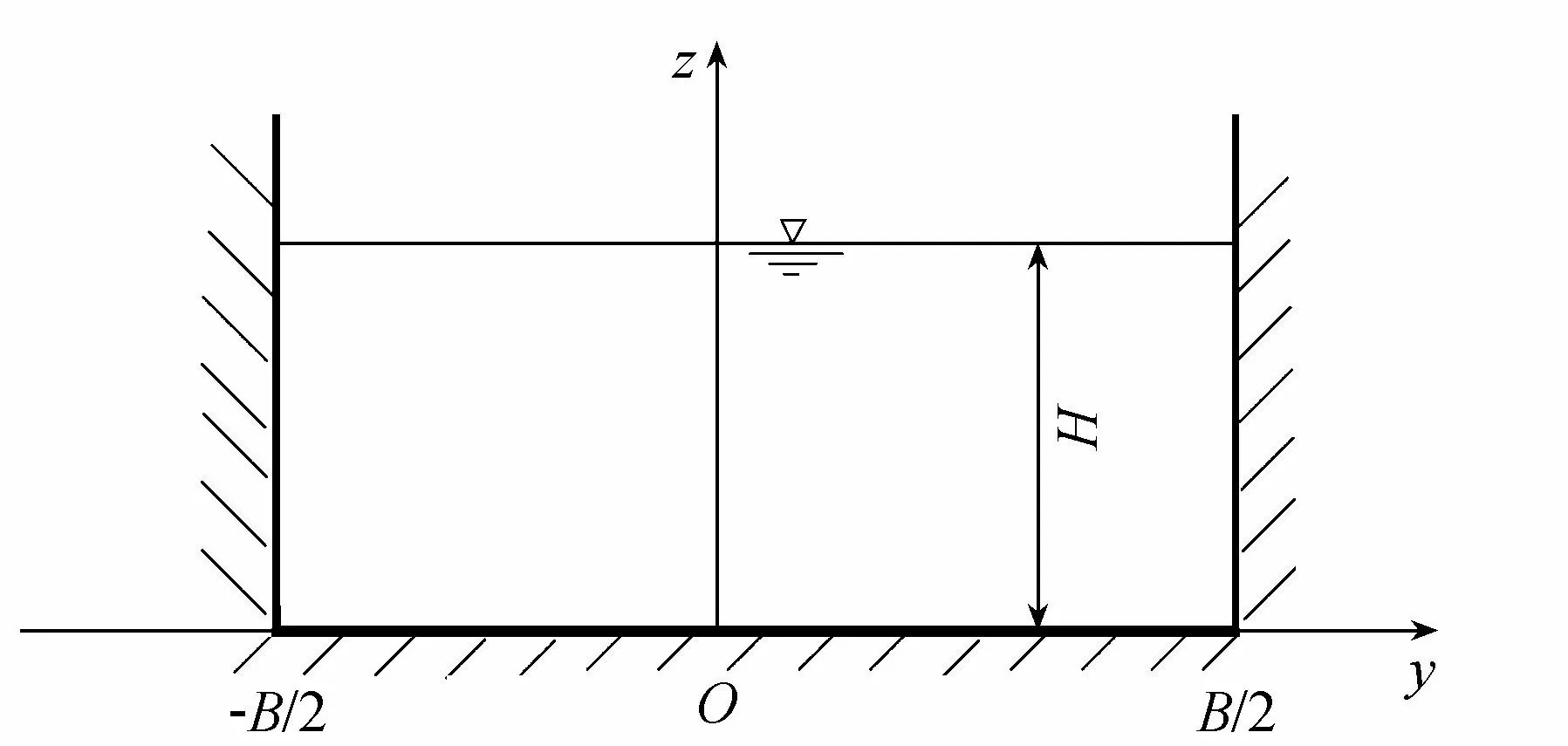
图1 矩形河流断面示意图

令y′=2y/B,对河宽进行归一化,式(4)化为

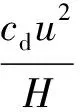
(5)

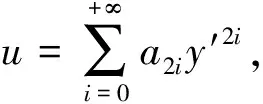
(6)

(7)

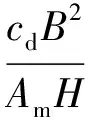
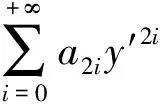
当断面最大流速umax已知时,则系数a0=umax,再代入式(6)和式(7),即可得到不同幂次的系数;当umax未知时,利用岸边界位置流速为零的条件,得到

(8)

联立式(6)(7)(8),可以得到不同幂次项的系数。在实际应用求解中,幂级数项数一般可取6～10项,而对于宽深比较大的河流,所取项数则相应增加。

将计算工况设置为H=1.0 m,改变宽深比B/H=10、50、100、150、200,Am=1.0 m2/s,cd=0.001,J=0.000 75,计算结果如图2所示。由图可2见,随宽深比增加,断面流速更加均匀:当深度一定时,随着河宽的增加,水流受岸边摩擦力的影响减弱,流速分布更加趋于均匀,符合水流的运动规律,说明所得到的幂级数解是合理的。

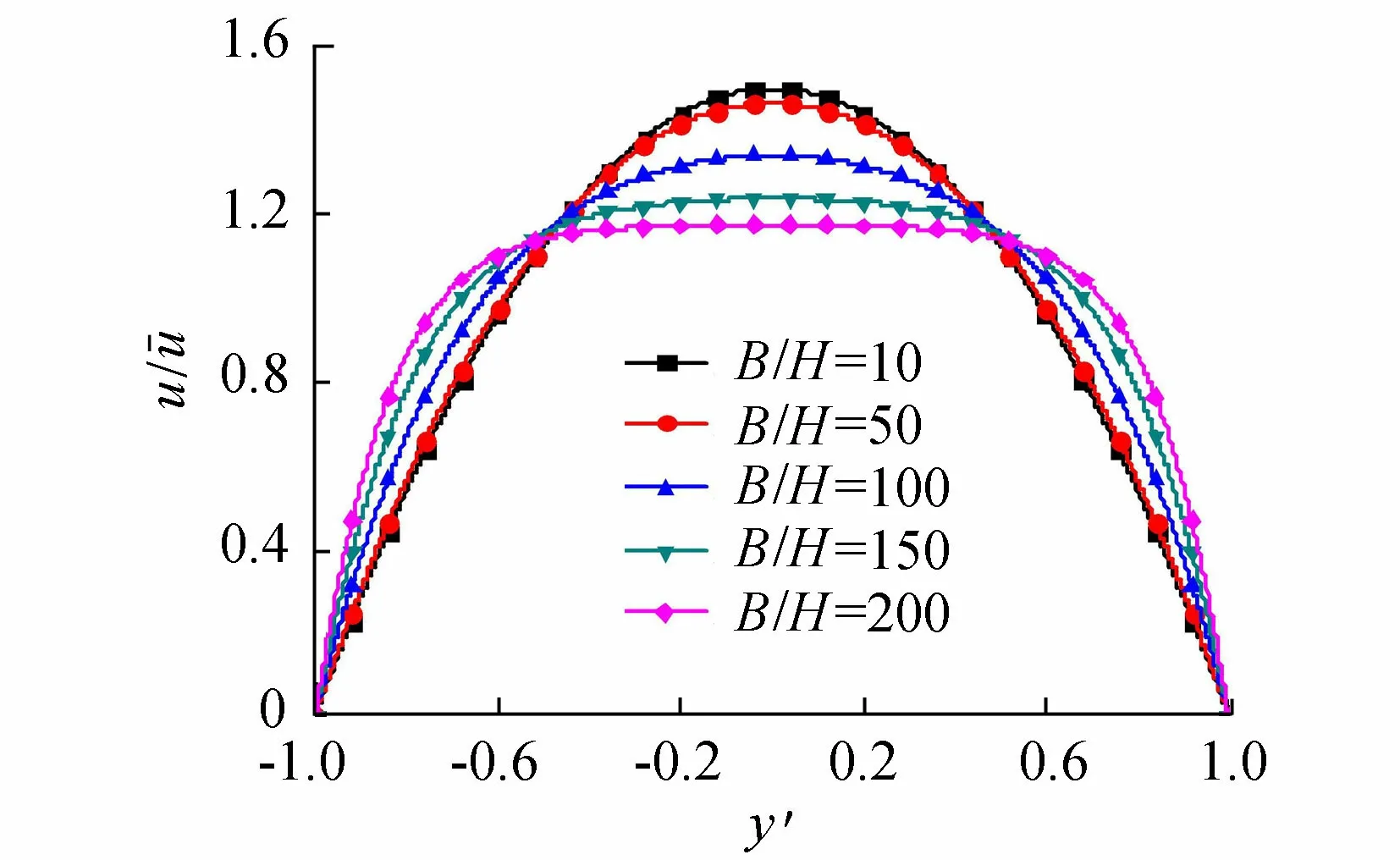
图2 矩形断面纵向流速分布

1.2 矩形断面纵向离散系数计算

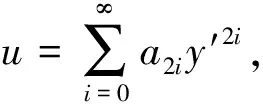
(9)

将其代入式(1),可得:

(10)

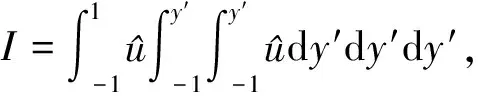
(11)

其中,三重积分

(12)

2 天然河流纵向离散系数计算

2.1 计算条件

2.2 结果与讨论

为分析本文计算方法计算结果的精度,采用对数比偏差KDR、对数平均绝对误差Me和对数均方根Rms这3个统计指标进行评价,定义如下:

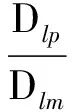
(13)

(14)

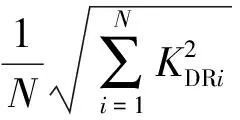
(15)

式中:Dlp为本文公式计算值;Dlm为实测值。

对数比偏差反映计算值与实测值的接近程度,当计算值与实测值之比越接近1时,则KDR越接近0,而KDR∈(-0.3,0.3)时,则计算值与实测值比值为0.5～2。对数平均绝对误差反映出计算值与实测值的整体偏离情况，对数均方根反映计算值与实测值的离散情况，对数平均绝对误差和对数均方根值越接近于0,说明计算值与实测值越接近,方程预测效果越好。

将本文公式计算值与实测值比较(图3),可见本文公式计算值较为均匀地分布在实测值两侧,但也存在一定的偏离,这主要是由于本文流速的幂级数解是基于矩形断面均匀流假定得到的,而天然河流的断面形式多种多样,将其统一概化为水面宽度与平均水深的矩形断面,会出现一定程度的失真,纵向离散系数的计算值和实测值之间存在一定的误差。

图3 纵向离散系数计算值与实测值的比较

将本文公式计算值与理论性较强的Wang等[11]、Deng等[13]的公式计算值进行了比较,结果见图3。由图3可看出,本文公式计算精度优于Wang等[11]的公式,但和Deng等[13]的公式相比则偏低。这是由于Deng等[13]的公式在离散系数的推导中流速分布由谢才公式计算,而谢才公式基于天然河流大量数据得到,对于自然河流具有更好的适用性。本文的流速幂级数解是基于矩形断面均匀流条件下的动力学方程得到的,故在将自然河流概化为矩形断面过程中出现了一定程度的失真。尽管如此,由于流速分布公式的物理意义相较谢才公式更为明确且计算精度总体不低于其他公式,本文计算方法仍然具有一定的意义。

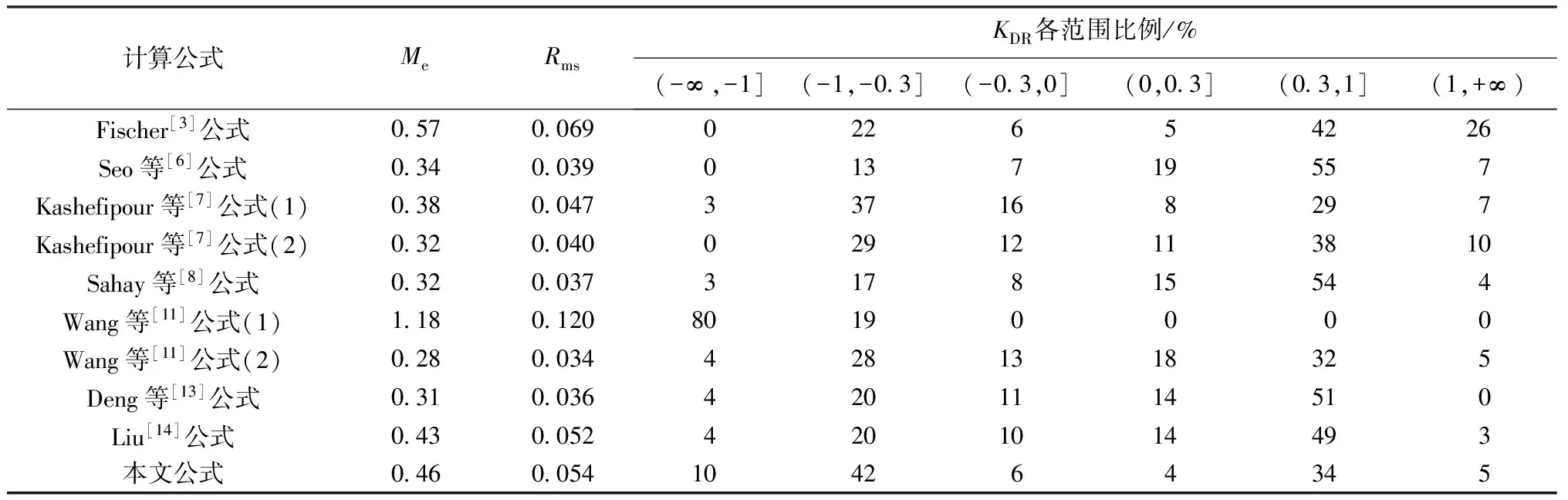
表1 不同纵向离散系数经验公式对比分析

为进一步分析KDR的误差与宽深比的关系,图4给出了不同宽深比下的误差分布情况。当宽深比较小时,本文公式计算值和Deng等[13]的公式计算值与实测值偏差处在相对合理的区间,而当宽深比大于100时,则所有理论公式计算结果的误差都会增大。

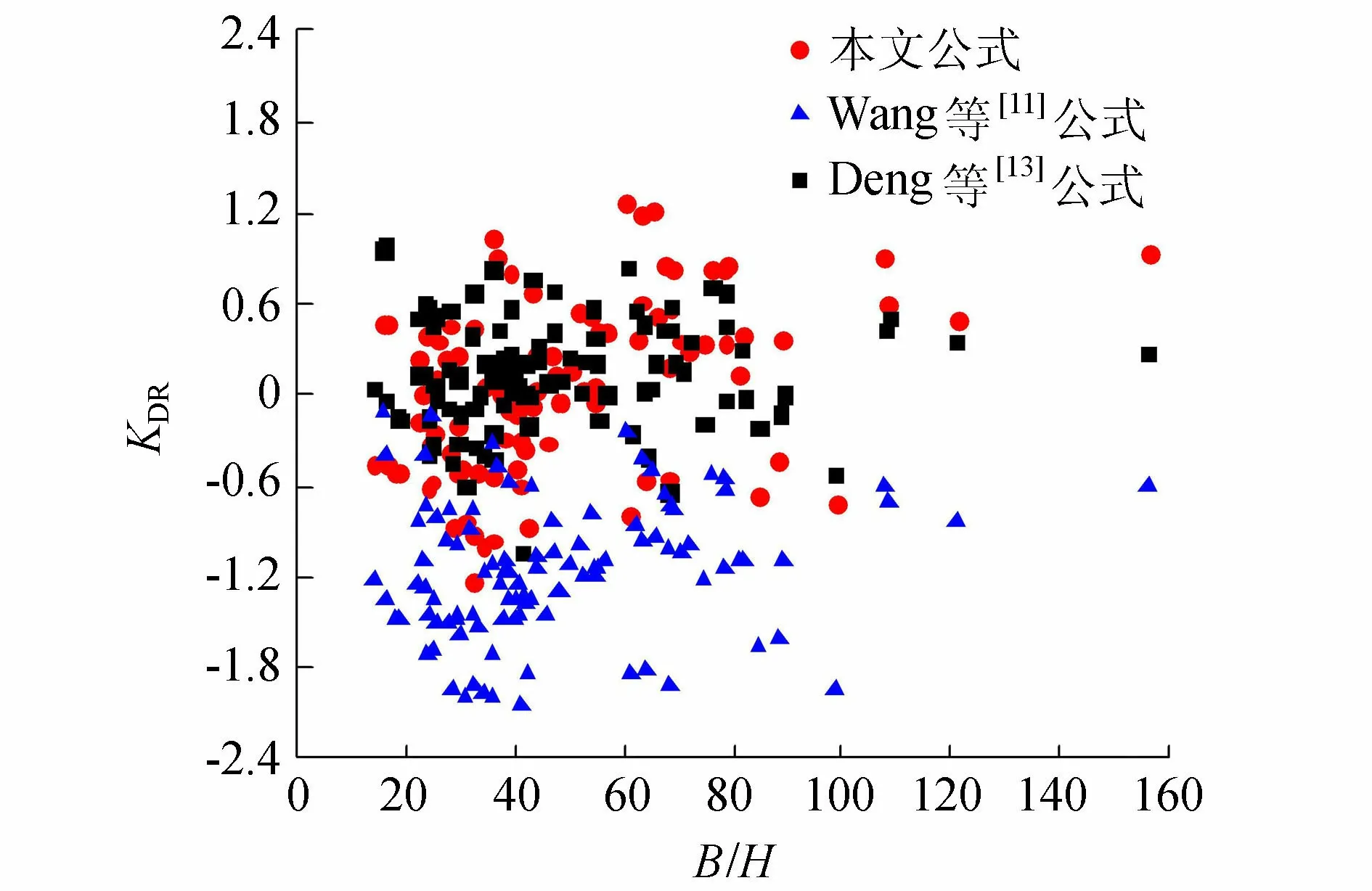
图4 对数比偏差与宽深比的关系

本文公式计算值与前人公式的计算值对比分析见表1,本文公式对于104条天然河流计算值的KDR分布在(-1,1)区间的比例为90%,即计算值与实测值基本在一个量级,与其他传统公式在同一水平;对数平均绝对误差Me为0.46,即本文公式整体计算值在实测值的0.34～2.8倍之间;对数均方根Rms为0.054,计算结果波动性不大,与各传统公式计算值误差相比相差不大,处于居中水平。

3 结 语

基于一维均匀恒定流控制方程,利用幂级数解法得到断面流速分布表达式,该解法能够较好地反映流体运动的力学机制,且形式简单,易于计算,与天然河流流动规律相吻合。通过将流速分布的幂级数解代入Fischer理论公式推导了矩形明渠纵向离散系数计算方法,该方法物理机制明确,可根据精度要求确定求解项数。将该纵向离散系数计算方法推广到天然河流中,并利用104条天然河流的实测资料进行了验证,结果显示计算值和实测值量级一致,能够反映天然河流的离散特性。

[1] TAYLOR G. The dispersion of matter in turbulent flow through a pipe[J]. Proceedings of the Royal Society of London, 1954, 223(1155):446-468.

[2] ELDER J W.The dispersion of marked fluid in turbulent shear flow[J].Journal of Fluid Mechanics,1959,5(4):544-560.

[3] FISCHER H B,LIST J,KOHR C Y,et al.Mixing in inland and coastal water [M].New York: Academic Press,1979:81-147.

[4] 李骏旻,黄平,李毅能,等.近似拟合法确定离散系数的适用性和选点策略[J].水利水电科技进展,2008,28(5):10-12.(LI Junmin,HUANG Ping,LI Yineng,et al.Applicability of approximate fitting method in estimation of longitudinal diffusivity coefficient[J].Advances in Science and Technology of Water Resources,2008,28(5):10-12.(in Chinese))

[5] 顾莉,华祖林.天然河流纵向离散系数确定方法的研究进展[J].水利水电科技进展,2007,27(2):85-89.(GU Li,HUA Zulin.Advances in determination of longitudinal dispersion coefficient of natural rivers[J].Advances in Science and Technology of Water Resources,2007,27(2):85-89.(in Chinese))

[6] SEO I W,CHEONG T S.Predicting longitudinal dispersion coefficient in natural streams[J].Journal of Hydraulic Engineering,1998,124(1):25-32.

[7] KASHEFIPOUR S M,FALCONER R A.Longitudinal dispersion coefficients in natural channels[J].Water Research, 2002,36(6):1596-608.

[8] SAHAY R R,DUTTA S.Prediction of longitudinal dispersion coefficients in natural rivers using genetic algorithm[J]. Hydrology Research,2009,40(6):544-552.

[9] 邓志强,褚君达.河流纵向分散系数研究[J].水科学进展,2001,12(2):137-142.(DENG Zhiqiang,CHU Junda.Longitudinal dispersion coefficient in natural rivers [J].Advances in Water Science,2001,12(2):137-142.(in Chinese))

[10] 陈永灿,朱德军.梯形断面明渠中纵向离散系数研究[J].水科学进展,2005,16(4):511-517.(CHEN Yongcan,ZHU Dejun.Study on longitudinal dispersion coefficient in open channel trapezoidal cross-section [J].Advances in Water Science,2005,16(4):511-517.(in Chinese))

[11] WANG Y, HUAI W. Estimating the longitudinal dispersion coefficient in straight natural rivers[J]. Journal of Hydraulic Engineering, 2016, 142(11):04016048.

[12] ZENG Yuhong,HUAI Wenxing.Estimation of longitudinal dispersion coefficient in rivers[J].Journal of Hydro-Environment Research,2014,8(1):2-8.

[13] DENG Zhiqiang,SINGGH V P,BENGTSSON L.Longitudinal dispersion coefficient in straight rivers[J].Journal of Hydraulic Engineering,2001,127(11):919-927.

[14] LIU H.Predicting dispersion coefficient of streams[J].Journal of the Environmental Engineering Division,1977,103(1): 59-69.

Computationoflongitudinaldispersioncoefficientinopenchannelsbasedonpowerseriessolutiontovelocitydistribution//

ZHANG Wenjun,HU Yu,REN Huatang,XIA Jianxin

(CollegeofLifeandEnvironmentalSciences,MinzuUniversityofChina,Beijing100081,China)

The longitudinal dispersion coefficient is usually computed directlyby empirical formulas or indirectly through introducing empirical formulas during the solution tovelocity distributions,which cannot fully reflect the physical mechanisms of dispersion.Based on the one-dimensional governing equation of river dynamics, a method to calculate longitudinal dispersion coefficient involving a power series solution to velocity distributionwas proposed.This formulation has been extended to the applications in 104 natural rivers with simplified rectanglecross-sections.The computed values are in the same order of magnitudes with the measured ones, indicating acceptable results.

longitudinal dispersion coefficient; open channel; power series; velocity distributions

国家自然科学基金(51479218)

张文俊(1992—),男,硕士研究生,主要从事环境水力学研究。E-mail:s151093@muc.edu.cn

任华堂(1976—),男,副教授,博士,主要从事环境水力学研究。E-mail:renhuatang@muc.edu.cn

10.3880/j.issn.1006-7647.2017.06.008

TV133

A

1006-7647(2017)06-0044-04

2016-12-11 编辑：熊水斌)