BDS三频与双频模糊度解算性能分析

严超,徐梅,徐炜,张广汉,杜文选

(安徽理工大学 测绘学院，安徽 淮南 232001)

BDS三频与双频模糊度解算性能分析

严超,徐梅,徐炜,张广汉,杜文选

(安徽理工大学 测绘学院，安徽 淮南 232001)

全球导航卫星系统(GNSS)已进入多频多系统时代。针对两条短基线,对比分析BDS三频与BDS/GPS三频对于BDS双频与BDS/GPS双频在模糊度固定率、成功率及定位精度等方面的改善情况。结果表明，BDS三频与BDS/GPS三频可有效提高BDS双频与BDS/GPS双频的固定率和成功率,但BDS三频与BDS/GPS三频对于BDS双频与BDS/GPS双频的定位精度基本上没有改善。

BDS双频;BDS/GPS双频;BDS三频;BDS/GPS三频;模糊度解算

0 引 言

模糊度快速准确解算是载波双差高精度定位中的核心问题,直接关系到定位应用的准确性和时效性[1-2]。杨元喜院士提出中国未来在卫星导航定位主要发展方向为多模多频、多GNSS融合导航定位理论研究与算法研究[3]。目前,新一代的全球导航卫星系统都采用了多频信号体制。现代化之后的全球定位系统(GPS)在已有L1和L2信号之外又新增了L5信号;而我国的北斗导航系统(BDS)所有卫星都能播发B1、B2和B3三个频点的导航信号[4]。多频信号的引入有助于提高载波信号模糊度解算的效率和可靠性;多系统融合可以有效地增加可观测卫星数量,增强了定位的几何结构,对改善单系统定位中可视卫星数量较少、观测环境遮挡等特殊环境下的定位精度及稳定性有较大的意义[5]。

双频模糊度解算已取得一定成效[6-8]。文献[6]选择方差较小的宽巷组合进行模糊度分组搜索,实现GPS单历元模糊度解算;文献[7]利用LAMBDA方法搜索3组最佳宽巷模糊度组合,实现BDS单历元基线解算;文献[8]基于伪距和宽巷载波相位双差观测方程,实现GPS/BDS组合系统单历元基线解算。三频模糊度解算也取得了显著成果[5,9-12]。文献[9]和文献[10]分别提出了适用于短基线模糊度解算的三频载波模糊度解算(TCAR)和级联整数解算(CIR)算法,两者的原理本质上相同,即按照固定难度从小到大依次固定超宽巷、宽巷和窄巷模糊度;文献[11]针对TCAR方法无法估计电离层延迟的问题,提出了一种附加估计电离层延迟的改进TCAR方法;文献[12]基于有几何模型,使用LAMBDA方法依次固定超宽巷、两个宽巷、两个无电离层组合窄巷模糊度,最后使用模糊度固定的两个无电离层组合实现BDS三频短基线单历元基线解算;文献[5]首先固定(0,-1,1)与(1,4,-5)两个超宽巷模糊度,利用宽巷模糊度约束与两个无几何模型方程联立快速求解北斗基频双差模糊度。上述文献很好地阐述了双频、三频模糊度解算理论与方法,具有很高的参考价值。本文综合考虑上述文献的理论与方法,总结出双频与三频单历元基线解算数学模型,并利用两条短基线,对比分析BDS三频与BDS/GPS三频对于BDS双频与BDS/GPS双频在模糊度固定率、成功率及定位精度等方面的改善情况。

1 数学模型

1.1双频单历元基线解算数学模型

GPS、BDS伪距及载波相位宽巷双差观测方程可表示为

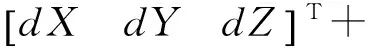
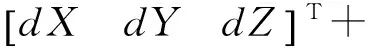
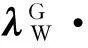
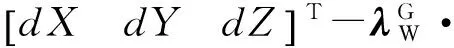
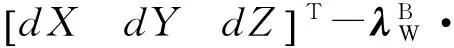
(1)

组合系统双差伪距和载波观测方程为

(2)

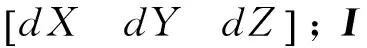
若GPS共视卫星为n(其中n≥2)颗,BDS共视卫星为m(其中m≥2)颗,则GPS单系统n≥4、BDS单系统m≥4和组合系统m+n≥5时,该方程不秩亏,由最小二乘可得:

(3)

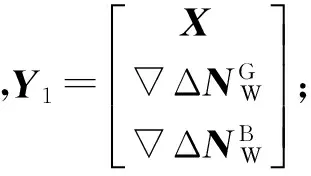
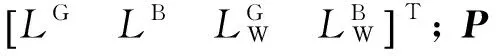
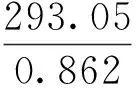
根据式(3)可以得到宽巷模糊度的初始值,选择方差较小的模糊度组成主模糊度组(当卫星较少时为4个,卫星较多时为卫星数的一半),并得到主模糊度组的实数解与协方差阵,用LAMBDA方法对主模糊度组进行解算。当主模糊度组固定后,就可以回代双差方差,改进所有参数,求得从模糊度组实数解与协方差阵,用LAMBDA方法对从模糊度进行解算,从而将所有的宽巷模糊度固定下来[6-8]。

利用已经固定的宽巷模糊度更新载波观测方程:

(4)

式中:λL1和λB1分别为GPS的L1和BDS的B1的波长;LL1和LB1分别为GPS的L1和BDS的B1载波双差与几何距离双差之差。

同理,由最小二乘法得:

(5)

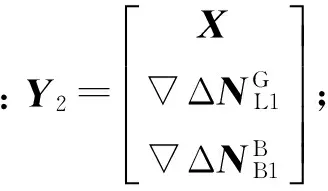
根据式(5)求得GPS的L1和BDS的B1的双差模糊度实数解与协方差阵,使用LAMBDA方法对其进行固定,当和准确固定后,回代到双差观测:

(6)

根据经典最小二乘原理得:

X=-(ATP1A)-1·(ATP1L)

(7)

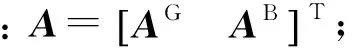
1.2三频单历元基线解算数学模型

三频情况下,频率的多样性可以提高无几何模糊度解算方法的可靠性。BDS三频观测时,可以对载波观测值进行组合可以得到超宽巷(EWL)组合,根据文献[5],[9]～[12],选择(0,-1,1)和(1,4,-5)两个超宽巷组合,EWL载波观测值与3个伪距观测值PB1,PB2以及PB3组成的基于几何模型的双差观测方程可表示为

(8)

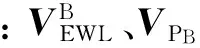
采用上述方法,可以成功固定(0,-1,1)和(1,4,-5)这两个WEL的和参数,将其看成高精度的距离观测值。由于短基线双差大气延迟误差较小,可以采用无电离层观测值消除电离层残差,因此可采用下式来求解BDS的基础模糊度

(9)

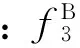
利用固定的北斗双差基础模糊度,可与GPS卫星的相应方程联合求解基线向量和GPS双差模糊度,解算模型为

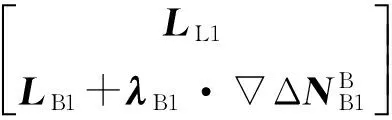
(10)

由经典最小二乘得:

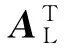
(11)

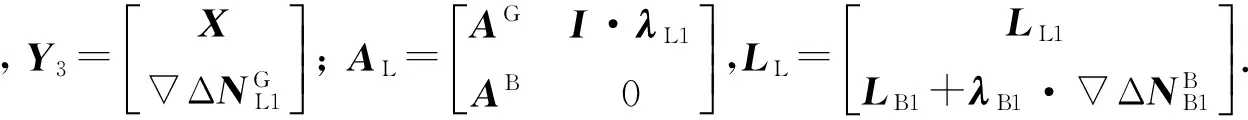
根据式(11)可以求得GPS的L1的双差模糊度实数解与协方差阵,使用LAMBDA方法对其进行固定,当和准确固定后,回代到式(7)就可以求解出dX、dY和dZ.

本文所述BDS双频为BDS的B1、B2频点,BDS三频为BDS的B1、B2、B3频点,BDS/GPS双频为BDS的B1、B2频点和GPS的L1、L2频点,BDS/GPS三频为BDS的B1、B2、B3频点和GPS的L1、L2频点。

2 实验分析

本文数据选用一条4.2 m基线和一条1.13 km基线,其中4.2 m基线来源于澳大利亚科廷大学GNSS研究中心实测数据,采样开始日期为GPS时2016年1月1日零时整,观测时长24 h,采样间隔30 s,共计2 880个历元;1.13 km基线来源于内蒙古自治区鄂尔多斯市的唐家会煤矿开采沉陷自动化监测系统数据,采样开始日期为GPS时2016年10月30日零时47分,观测时长5 668 s,采样间隔1 s,共计5 668个历元。卫星截止高度角均设置为15°.

2.1模糊度解算结果分析

本文对BDS和BDS/GPS采用上述所介绍的双频和三频单历元基线解算的数学模型进行单历元模糊度解算,解算结果的有效性检验可以从固定率和成功率两方面进行衡量[13-14]; 固定率检验是以设定Ratio阈值的方法来确定的。

固定率=满足阈值历元数/有效历元数

在实际解算中,可能会拒绝低于Ratio阈值的正确模糊度组或者接受大于Ratio阈值的错误模糊度组[15],所以4.2 m基线以澳大利亚科廷大学GNSS研究中心提供的坐标值作为参考值,1.13 km以内蒙古自治区鄂尔多斯市的唐家会煤矿开采沉陷自动化监测站GNSS网数据处理结果作为参考值。分别将各历元固定解与参考值进行比较,相同则认为是正确的。

成功率=正确固定历元数/有效历元数

两条基线解算的固定率与成功率如表1所示。

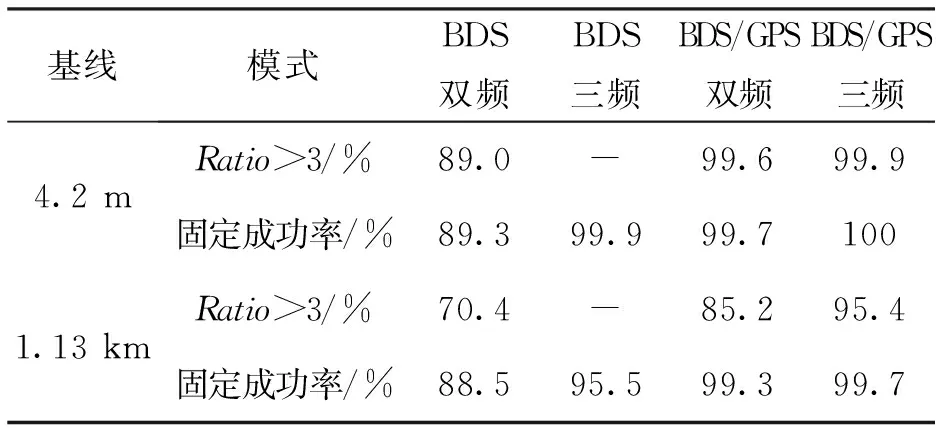
表1 模糊度固定结果统计

由表1可知,对于4.2 m和1.13 km基线,BDS三频成功率高于BDS双频,BDS/GPS三频成功率高于BDS/GPS双频,且BDS/GPS三频与BDS/GPS双频的固定率、成功率均高于BDS三频与BDS双频。总之,BDS三频与BDS/GPS三频分别有效地提高了BDS双频与BDS/GPS双频的固定率和成功率,BDS/GPS三频与BDS/GPS双频分别有效地提高了BDS三频与BDS双频的固定率和成功率。

2.2定位精度分析

本文在进行精度分析时,仅从定位结果角度出发,判断模糊度正确固定的历元的解算结果,与参考值作差,得出两条基线在WGS-84坐标系下X、Y、Z方向的基线偏差,结果如图1,图2所示,表2示出了两条基线解算结果的内符合精度。

由图1、图2和表2可知,无论4.2 m基线还是1.13 km基线,BDS三频与BDS/GPS三频在X,Y,Z方向定位偏差都比BDS双频与BDS/GPS双频要大,定位精度有所降低; BDS/GPS双频、BDS/GPS三频的离散性要分别比BDS双频、BDS三频低,精度也有所提高。所以采用上述所述的BDS三频与BDS/GPS三频单历元基线解算方法对于BDS双频与BDS/GPS双频的定位精度基本上没有改善。

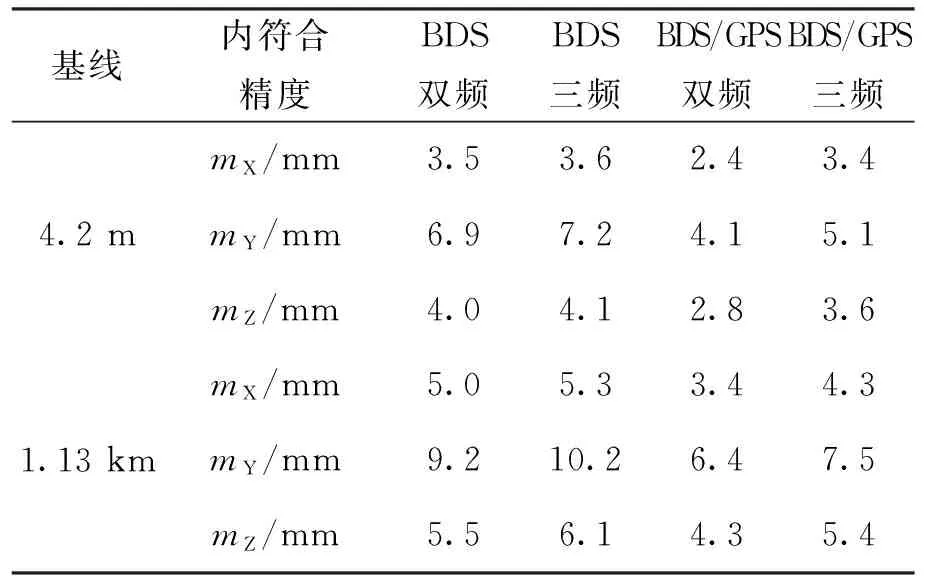
表2 定位精度统计

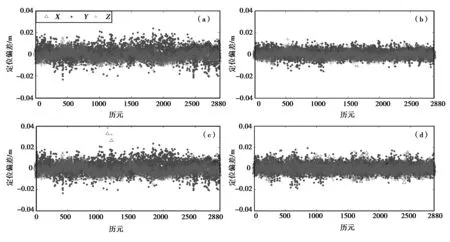
图1 4.2 m基线解算结果在X、Y、Z方向的偏差 (a)BDS双频; (b)BDS/GPS双频; (c)BDS三频; (d)BDS/GPS三频

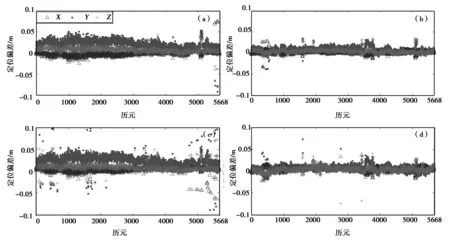
图2 1.13 km基线解算结果在X、Y、Z方向的偏差 (a)BDS双频; (b)BDS/GPS双频; (c)BDS三频; (d)BDS/GPS三频

3 结束语

通过BDS三频、BDS/GPS三频与BDS双频、BDS/GPS双频的单历元基线解算结果对比分析,可以得出以下结论:1) BDS三频与BDS/GPS三频分别有效地提高了BDS双频与BDS/GPS双频的固定率和成功率,BDS/GPS三频与BDS/GPS双频分别有效地提高了BDS三频与BDS双频的固定率和成功率;2) 虽然BDS/GPS双频、BDS/GPS三频相对于BDS双频、BDS三频定位精度有所改善,但BDS三频与BDS/GPS三频对于BDS双频与BDS/GPS双频的定位精度基本上没有改善。

[1] CHEN H Y, RIZOS C, HAN S.etal. An instant aneousambiguity resolution procedure suitable for medium-scale GPS reference station networks [J]. Survey Review, 37(291), 396-410.

[2] 李博峰, 沈云中. 附有约束条件的GPS模糊度快速解算[J]. 武汉大学学报(信息科学版), 2009, 34(1):117-121.

[3] 杨元喜. 导航与定位若干注记[J]. 导航定位学报, 2015(3):1-4.

[4] 谢建涛,郝金明,韩聪,等. BDS单历元TCAR算法优化研究[J]. 测绘科学技术学报, 2016, 33(1):6-10.

[5] 吕伟才,高井祥,王坚,等. 北斗三频约束的短基线模糊度单历元算法[J]. 中国矿业大学学报, 2015, 44(6):1090-1096.

[6] 祝会忠,高星伟,秘金钟,等. 一种GPS整周模糊度单历元解算方法[J]. 测绘科学,2011,36(4):9-11.

[7] 唐卫明,邓辰龙,高丽峰. 北斗单历元基线解算算法研究及初步结果[J]. 武汉大学学报(信息科学版),2013,38(8):897-901.

[8] 陶庭叶,王志平,蒋俊儒. GPS/BDS单历元基线解算中随机模型的确定[J]. 大地测量与地球动力学,2015,35(4):649-652.

[9] HATCH R, JUNG J, ENGE P,etal. Civilian GPS: The benefits of three frequencies[J]. GPS Solutions, 2000, 3(4):1-9.

[10] HAN S, RIZOS C. Single-epoch ambiguity resolution for real-time GPS attitude determination with the aid of one-dimensional optical fiber gyro[J]. GPS Solutions, 1999, 3(1):5-12.

[11] TANG W, DENG C, SHI C,etal. Triple-frequency carrier ambiguity resolution for Beidou navigation satellite system[J]. GPS Solutions, 2014, 18(3):335-344.

[12] 刘炎炎, 叶世榕, 江鹏,等. 基于北斗三频的短基线单历元模糊度固定[J]. 武汉大学学报(信息科学版), 2015, 40(2):209-213.

[13] 刘经南, 邓辰龙, 唐卫明. GNSS整周模糊度确认理论方法研究进展[J]. 武汉大学学报(信息科学版), 2014, 39(9):1009-1015.

[14] DENG C L, TANG W M. Reliable Sing-epoch ambiguity resolution for short baselines using GPS/BeiDou system[J]. GPS Solutions, 2014, 3(18):375-386.

[15] TEUNIWWEN PJ G, VERHAGEN S. The GNSS ambiguity ratio-test revisited:a better way of using it[J]. Suvery Review, 2009(41):138-151.

PerformanceAnalysisofBDSTriple-frequencyandDual-frequencyAmbiguityResolution

YANChao,XUMei,XUWei,ZHANGGuanghan,DUWenxuan

(SchoolofGeomatics,AnhuiUniversityofScienceandTechnology,Huainan232001,China)

The global navigation satellite system (GNSS) has entered the age of multi-frequency and multi-system. In terms of the two short baselines, compared to BDS dual-frequenc and BDS/GPS dual-frequency,BDS triple-frequency and BDS/GPS triple-frequency are analysed in the ambiguity fixed rate, success rate and positioning accuracy.The results showed that BDS triple-frequency and BDS/GPS triple-frequency can effectively improve the ambiguity fixed rate and success rate of BDS and BDS/GPS dual-frequency,but it can not improve the positioning accuracy basically.

BDS dual-frequency; BDS/GPS dual-frequency; BDS triple-frequency; BDS/GPS triple-frequency; ambiguity resolution

10.13442/j.gnss.1008-9268.2017.04.011

P228.4

A

1008-9268(2017)04-0060-06

2017-05-07

国家自然科学基金(批准号:41474026)); 淮南矿业(集团)有限责任公司项目(编号:HNKY-JTJS(2013)-28); 安徽理工大学2017年研究生创新基金(编号:2017CX2056)

联系人: 严超 E-mail:757261684@qq.com

严超(1993-),男,硕士研究生,主要研究方向为GNSS测量与数据处理、开采沉陷监测与数据处理。

徐梅(1992-),女,硕士研究生,主要研究方向为GNSS数据处理

徐炜(1992-),男,硕士研究生,主要研究方向为GNSS导航与数据处理。

张广汉(1992-),男,硕士研究生,主要研究方向为开采沉陷监测与数据处理。

杜文选(1992-),男,硕士研究生,主要研究方向为GNSS导航与定位。