侧风作用下高速列车的空气动力学初探

成 楠， 张明禄

(西南交通大学力学与工程学院， 四川成都 610031)

侧风作用下高速列车的空气动力学初探

成 楠， 张明禄

(西南交通大学力学与工程学院， 四川成都 610031)

用大涡模拟(LES)计算侧风影响下的简化了的高速列车环流。文章基于列车高度和来流速度，确定流动的雷诺数Re为5.5×108。在偏转角(在相对的侧风方向和列车前进方向的夹角)为90°情况下，获得计算结果。通过大涡模拟( LES)数值计算方法，对均匀定常侧风下高速列车的非定常空气动力特性进行了研究。计算结果分析表明，即使在均匀定常侧风下，列车所受空气动力也存在明显的非定常性。

高速列车； 侧风； 气动力； 非定常

由于高速列车不断升高的速度，高速列车遭受的空气动力问题越显突出[1]。列车行驶安全性与舒适性均和列车侧风问题有关，在众多列车空气动力问题中，列车侧风是一个重要问题。从世界范围来看，由于侧风引发的列车事故屡见不鲜，2007年，新疆一列车受大风影响导致出轨，造成了严重交通事故[2]。高速铁路发展的趋势是列车车体轻量化和行驶高速化，但与此同时，这种发展趋势也会使侧风导致列车倾覆的概率明显增加[3]。

为了提高在侧风下列车行驶的安全性，近几十年国内外研究人员进行了大量研究，包括通过风洞试验、实车试验及数值计算等方法，考察了列车在侧风下的空气动力特性[4-7]。但这些研究的主要结论是在侧风下对列车的定常(时间平均)空气动力特性以及列车运行稳定性受侧风风速波动的影响，而从最近几年才开始对列车在侧风下的瞬时流场以及列车所受空气动力的瞬时特性的研究。2004 年，Christina Rol n等人发表论文指出，在较大侧风偏转角情况下，列车的空气动力具有很强的非定常特点[3]; 2005年～ 2006年，Hassan Hemida 发表多篇论文[8-9]并根据计算结果指出，在侧风作用下列车所受的非定常空气动力的频率接近真实列车系统的固有频率。国内尚未见到关于列车在侧风下非定常空气动力方面的研究的相关文献。通过以上分析可以看出，在侧风下列车非定常空气动力特性的研究还未有系统的研究，尚属起步阶段。同时，已有部分研究结果指出，侧风作用在列车上的定常空气动力的大小不足以解释列车被大风吹翻的原因[11]。因此，研究侧风下列车非定常空气动力问题具有现实意义。

针对自然风速相对列车的偏转角为 90°的情况，本文通过大涡模拟(LES)数值计算方法，研究了车身所受空气动力的非定常特性以及列车周围非定常流场特性，最后根据研究结果，为列车侧风非定常空气动力特性提出了笔者的看法。

1 数值模型和计算方法

1.1 数值模型

为了将问题简化，同时突出所研究的侧风部分，本文研究是在自然风速的偏转角为 90°的情况，即风向为横向垂直于高速列车侧壁，且不考虑列车行驶方向的速度。侧风角和偏转角定义方式如图1所示。本次计算采用的实车模型是CRH2型高速列车，为减少计算量和计算时间，采取如下简化：(1)将列车分为头车、中间车和尾车，分别设为25.5 m、25 m和25.5 m，整辆列车为一连续刚体。(2)将列车表面简化成光滑曲面，认为表面的粗糙度各处一致，并假设表面摩擦力沿车身均匀分布。(3)在实际模拟计算中把列车底部的复杂结构去掉,使列车底面和地面间形成了一个狭缝，并用这个狭缝对流场的影响来模拟列车底部结构对流场的影响，本文中列车与地面间距设为0.2 m。

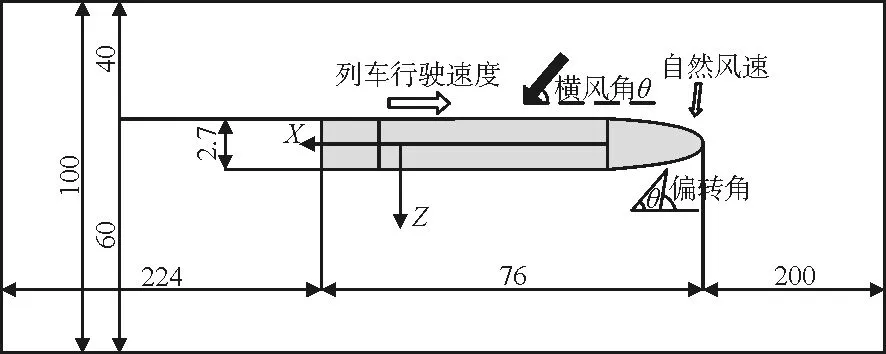
图1 列车与计算流域位置(单位:m)

1.2 计算域设定及网格划分

(1) 计算域。 将计算域划分为来流区和尾流区，根据绕流流场的基本特性，尾流区域取较大值。列车模型尾流区域的纵向长度大于3倍的列车模型总长度，列车模型前端的流场区域的纵向长度大于2倍的列车模型宽度，计算域高度大于10倍的车高[2]。计算域的几何尺寸为 500 m×40 m×100 m(图1)。

(2) 网格划分。采用非结构化网格，共生成500多万。为了保证网格质量，提高壁面函数应用于边界层模拟的准确性网格，在车体表面及地面处生成边界层网格，边界层网格的厚度为100 mm，增长比为1.2，共设置5层边界层网格。

1.3 边界条件

模拟列车附近的外流场采用相对运动条件。即假定列车静止，空气来流以与列车运行速度反向等值的速度vt绕流列车，侧风以速度vw吹向列车，二者的合成速度为v(图1)。

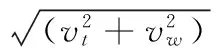
(2)出口边界条件。压力边界条件，出口压力取一个标准大气压强。

(3)计算域表面。由于选择的流场计算区域足够大，可认为外围边界对列车周围的流场的影响甚小，计算区域的外围边界设定为压力出口。

2 计算结果及其分析

列车速度vt= 350 km/h，侧风速度vw=30 m/s，侧风的偏转角为90°的列车表面压力分布。

从迎风侧静止压力图，可以看出头车前缘的正负压最大，其他位置不是危险截面(图2)。我们需要重视危险位置，把重要问题突出。其中负压比正压系数要多出50 %，因此列车在侧风下的行驶过程中，更可能被吸走，而不是吹走。

图2 静止压力和列车位置的关系

本研究将计算初始时间的部分删除，留下稳定计算结果，得出时间-侧力曲线图(图3)。

图3 头车、中间车和尾车的侧力值随时间的变化曲线

列车表面压力分布是在总体趋势不变的情况下, 随时间在均值附近波动, 这种波动的幅值及相应位置存在随机性。这种压力波动表明: 即使在定常侧风的情况下, 列车所受空气动力也存在明显的非定常性。由图3可以看出在侧风作用下，三个不同位置头车的侧力峰值最大，而且无论是幅值还是变化程度，中间车和尾车都相对头车较小，因此最应当受到关注的位置是头车。

而后，又采用了不同车速、风速和偏转角，依然得到相似的气动力幅值与列车位置的规律。

3 结论

本文基于计算流体力学和多体动力学仿真技术，对侧风下高速列车的空气动力学特征进行了数值模拟，可得到如下结论：

(1)受到极大关注的侧力在头车位置最为危险，接下来的研究应当集中关注头车的气动力情况。而在头车前缘的位置，压力系数最大，因此考虑最大受力位置时，头车的位置应当是首当其冲的。

(2)列车所受非定常力是由于侧风导致的非定常流场产生，并且列车所受非定常空气动力特性与其周围非定常流场特性之间存在对应关系。因此，有可能在风洞试验中，通过对列车周围非定常流场的测量得到列车在侧风下所受非定常空气动力特性。

[1] Raghu S Raghunathana, Kim H D, Setoguchi T. Aerodynamics of highspeed railway train [J] . Progress in Aerospace Sciences, 2002, 38: 469-514.

[2] 王丽丽. 新疆步入高铁时代[J]. 大陆桥视野, 2014(11):26-30.

[3] Christina Rol n, Thomas Rung, Don Wu. Computational modeling of crosswind stability of highspeed trains[DB/OL]. ECCOMAS 2004.

[4] 王厚雄, 林荣生. 列车的侧风倾覆力矩特性[J] . 空气动力学学报, 1983, 1(3) :72-77.

[5] 高广军, 田红旗, 姚松, 等. 兰新线强侧风对车辆倾覆稳定性的影响[J] . 铁道学报, 2004, 26(4): 36-40.

[6] Cooper K. Effect of crosswinds on trains[J] . Journal of Fluids Engineering, Transactions of the ASME, 1981, 103(1): 170-178.

[7] C J Baker, J Jones, F LopezCalleja, J Munday. Measurements of the cross wind forces on trains [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2004, 92(7): 547-563.

[8] Hassan Hemida, Sinisa Krajnovic, Lars Davidson. Large eddy simulation of the flow around a simplified high speed train under the influence of a crosswind [C]//AIAA .17 th AIAA Computational Fluid Dynamics Conference2005, AIAA 2005-5354.

[9] Hassan Hemida, Sinisa Krajnovic. Numerical study of the unsteady flow structures around trainshaped body subjected to side winds [DB/OL] . ECCOMAS CFD 2006.

[10] 王兆军, 张军, 朱春华, 等. 南疆列车倾覆事故的动力学因素分析[J]. 力学与实践, 2007, 29(5) : 87-89.

[11] Lilly K. A Proposed Modification of the Germano Subgrid Scale Closure Model[ J] . Physics of Fluids, 1992, 4(3) :633-635.

[12] 陶文铨. 数值传热学[M]. 2 版. 西安:西安交通大学出版社, 2005:218-226.

U260.11

A

[定稿日期]2017-05-05

成楠(1991～)，男，硕士，研究方向为高速列车空气动力学。