差分进化算法在气动力参数辨识中的应用

简兆圣，艾剑良

(复旦大学 航空航天系，上海200433)

差分进化算法在气动力参数辨识中的应用

简兆圣，艾剑良

(复旦大学 航空航天系，上海200433)

差分进化算法是一种新兴的优化算法，与最小二乘法等梯度类算法相比，它能够进行全局寻优且对初值不敏感，具有广泛的应用前景.建立某型飞机刚体运动的6自由度非线性动力学模型，在叠加一定比例白噪声的情况下获得其仿真数据，使用差分进化算法辨识出该型飞机的纵向运动气动力参数，辨识结果与真实值较为吻合，证明该算法是可行的.多组试验表明：对于该型飞机的动力学模型和仿真数据，使用差分进化算法的辨识结果与使用最小二乘法、普通粒子群算法的辨识结果相比，具有更高的精度和更强的鲁棒性.

气动力参数辨识；差分进化算法；粒子群算法；非线性系统辨识

建立一套高置信度飞行器仿真系统的关键是建立一个精确的气动力数学模型.建立气动力数学模型的前提是获得该飞机准确的气动参数.系统参数辨识方法是获取气动参数的有效方法，不仅能够作为理论计算和风洞试验方法的有效辅助，还能够利用飞机真实飞行环境中的输入和响应输出，反向推导辨识其系统参数直接获得精确的数学模型.特别是对于小型飞行器，直接辨识获取其气动参数可以避免繁琐而昂贵的风洞试验，简化了设计流程，并降低了成本.所以，如何设计高效准确的参数辨识算法重新成为近年来研究的重点.

目前工程中广泛应用的参数辨识方法主要为基于最小二乘准则和极大似然准则的梯度类算法，这些方法将参数辨识问题转化成一个极值优化问题，使数学模型的输出与实测值的偏差达到最小.对于线性系统，使用基本最小二乘法、极大似然法和它们的改进算法能获得较高辨识精度，文献[1]指出通过一定的手段可以使系统相对于参数是线性的，从而将最小二乘方法应用于非线性参数辨识中，文献[2]给出了非线性动力学系统极大似然法的完备方程组，采用牛顿-拉夫逊迭代算法取泛函极值，成功地将极大似然法应用于非线性参数辨识，该算法也成为了国内外飞行器设计工作中应用最广泛的参数辨识方法.文献[3]为近年来学者对最小二乘法的研究和发展，一定程度上体现了这些经典辨识算法的实用性和生命力.

然而，基于目标函数梯度构造的优化方法有其局限性，当目标函数不连续或系统存在迟滞时无法求取梯度值.由于这类算法对选取的初始参数十分敏感，求解时容易陷入初值附近的局部最优解，所以也要求掌握足够的先验知识，以选取合适的初值[4].

近20年来，随着最优理论的发展和计算机计算能力的提高，智能辨识算法由于其强大的全局搜索能力和不受初值影响的特点，已被逐步广泛应用于参数辨识中.文献[4]实现了粒子群优化(Particle Swarm Optimization,PSO)算法和文献[5]实现了基于遗传算法(Genetic Algorithm,GA)的气动力参数辨识.文献[6]将PSO算法及其改进形式应用于小型无人机的气动力参数辨识，并取得了较好的辨识效果.

差分进化(Differential Evolution,DE)算法最初由Storn和Price于1995年首次提出[7]，它模拟了自然界的生物种群进化，是一种基于全局随机搜索策略的随机启发式搜索算法.由于其在优化求解过程中不依赖于被优化问题的信息，而是根据整个种群的动态变化来调整搜索策略，因此能够解决传统优化方法难以求解的复杂系统的优化问题.DE算法已成功应用于复杂系统的参数辨识[8-9].

本文将DE算法应用于飞行器气动力参数辨识问题，对某型给定气动力参数真实值的飞机进行运动仿真试验，采集仿真试验的输入输出信号，利用最小二乘法、普通PSO算法和DE算法逆向辨识出该飞机的气动力参数，比较辨识值和真实值，根据其接近程度和收敛速度来判断辨识算法的优劣性.

1 DE算法的基本理论

DE算法的主要思想：首先从一个随机产生的初始种群中任意选出两个个体，对它们相减得到的差分向量进行加权，将加权之后的结果与第3个个体相加获得变异个体，变异个体有一定几率参与适应度计算，若该变异个体的适应度优于旧个体的适应度值，则该变异个体被“选择”为取代旧个体的新个体，并应用于下一代的进化操作，如此不断地迭代计算，产生适应度最优的新个体即为所求的最优解[7].

DE算法在整体结构上与其他进化算法类似，有多种变种，本文使用的是标准差分进化算法.

标准DE算法主要包括生成初始种群、变异操作、交叉操作、选择操作这4个步骤[7].反复执行变异操作、交叉操作、选择操作这3个步骤，直至达到最大迭代次数G或满足终止条件，标准DE算法的基本运算流程如图1所示.

图1 标准DE算法的运算流程图Fig.1 Flow chart of the normal DE algorithm

2 气动力参数辨识模型

以某型飞机纵向运动气动力参数辨识为例，介绍DE算法在气动力参数辨识中的应用.

将飞机视为刚体，对其飞行环境进行一定简化，则其6自由度非线性运动方程组用机体坐标系表示成式(1)～(4)：

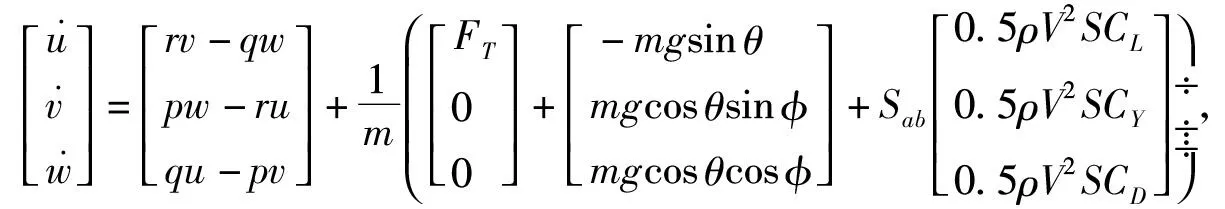
(1)

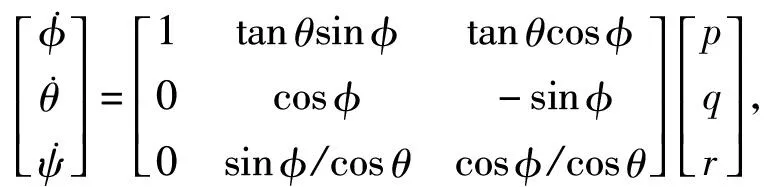
(2)

(3)

式中：

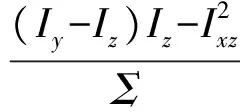
(4)

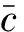
为简化辨识复杂度，只对飞机施加俯仰舵偏信号，即以升降舵偏角作为激励输入.将飞机视为面对称布局飞行器，并简化飞机运动，使φ=ψ=p=r=0，则飞机其他的横侧向状态量亦等于0.所以，飞机状态的部分观测方程可以写成式(5)～(7)：

(5)

(6)

(7)

纵向气动参数常采用式所示数学模型：

其中：δe为升降舵偏角；CD0，CD α，CL0，CL α，CL δe，Cm0，Cm α，Cm q和Cm δe为待辨识参数，其中CD0，CL0，Cm0分别为零升阻力系数、零升升力系数和零升俯仰力矩系数，其余为阻力、升力和俯仰力矩对攻角、俯仰角速率、升降舵偏角的气动导数.

采用普通PSO算法和DE算法对这9个待辨识参数进行辨识.易知，观测方程(5)，(6)中含有相同的5个待辨识参数，观测方程(7)中含有4个待辨识参数.为提高辨识效率，参数辨识分为两部分进行，通过观测方程(5)，(6)获得数据对CD0,CD α,CL0,CL α和CL δe这5个参数进行辨识，即在普通PSO算法和DE算法中设置每个个体具有5个维度；通过观测方程(7)获得数据对参数Cm0，Cm α，Cm q和Cm δe进行辨识，每个个体设置为4个维度.

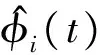
(9)

中的辨识误差J达极小，此时的最优个体即为辨识所得参数.

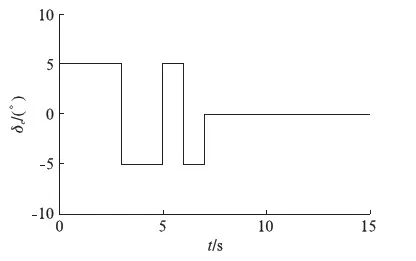
图2 “3211”仿真输入信号示意图Fig.2 The diagram of simulated signal “3211”

3 仿真试验与辨识结果

3.1仿真输入设计

为了验证各种算法的辨识能力，首先对该飞机6自由度非线性模型进行仿真试验.输入设计采用“3211”信号输入[2]，即使升降舵交替偏转，持续时间t为3，2，1和1s，幅度δe为5°，作为经典的“3211”激励信号，它能够使飞机响应振荡幅度增大，振荡次数增多，能更好地激发出与待辨识参数相关的运动模态，为辨识提供更多的信息.激励信号如图2所示.

3.2纵向气动力参数辨识结果

本文中分别采用最小二乘算法、普通PSO算法和DE算法对这9个气动力参数进行辨识.基于先验知识，设置CD0，CD α，CL0，CL α和CL δe这5个参数的辨识范围均为[0，5]，Cm0，Cm α，Cm q和Cm δe的辨识范围均为[-5，0].

普通PSO算法的参数设置采取常规设置方式：粒子群规模为100，加速度因子取为c1=1.5，c2=2，迭代次数为G，采用线性递减的惯性权重，惯性权重采用0.9线性递减到0.1的策略；DE算法的种群规模同样设为100，变异因子eF和交叉因子eCR根据常规设置方式分别取为0.7和0.6，迭代次数为G；当G取100,200,500和1000时，比较普通PSO算法和DE算法的辨识结果，见表1.可以看出，DE算法的辨识结果迅速收敛，从200代开始辨识值稳定地等于给定值，而普通PSO算法辨识结果收敛较慢，且迭代1000代后结果和给定值仍有偏差.

结果表明：对于该模型，DE算法相比于普通PSO算法具有更强的求解能力和全局收敛能力，且结果保持良好的鲁棒性.

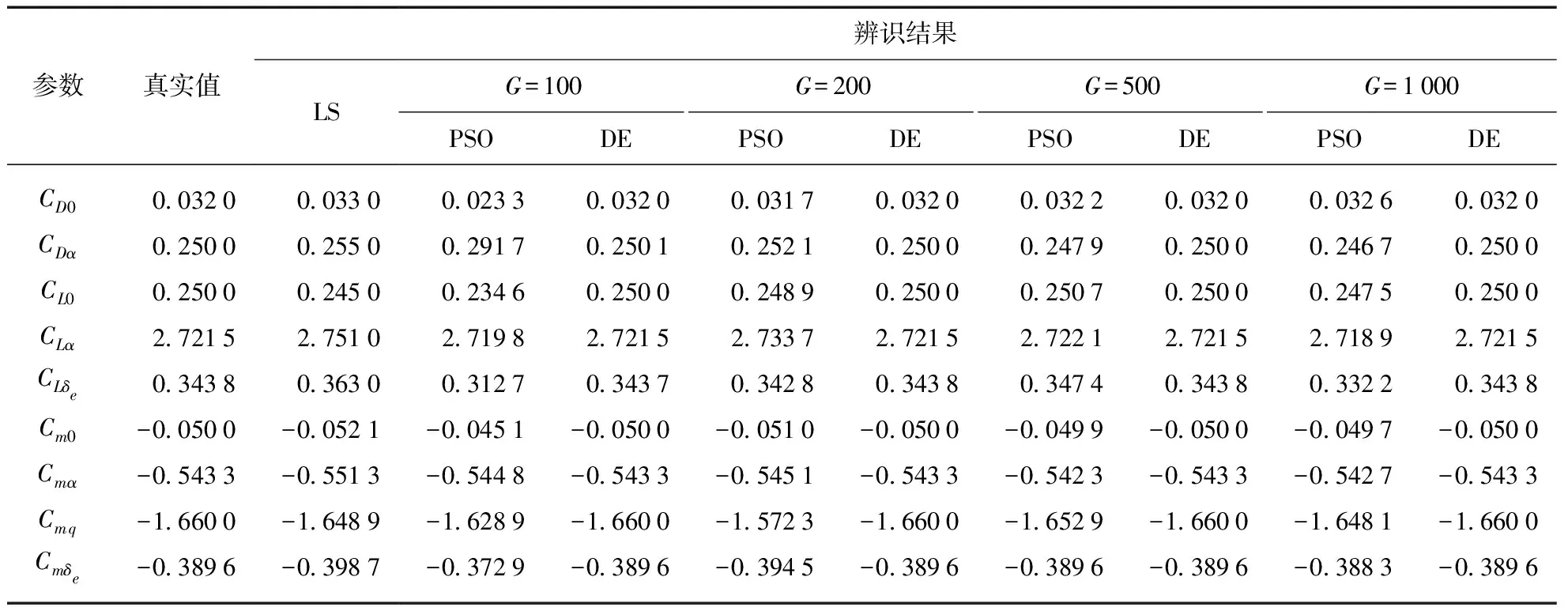
表1 纵向气动力参数辨识结果与真实值比较Tab.1 Comparison between the identification results by different methods and the true value

Sn(i)=(1+noise×((1-(-1))×rand+(-1)))×S(i)i=1,2,…，N，

(10)

其中：S(i)和Sn(i)分别为测量数据和叠加噪声的测量数据；式中noise取2%，5%，8%，表示叠加白噪声的均值为0，标准差分别为0.02，0.05和0.08.采用与此前相同设置的普通PSO算法和DE算法，迭代500代辨识系统参数，辨识结果如表2所示.

表2 在不同强度的白噪声干扰下的辨识结果Tab.2 Identified parameters with different strength of noise

图3 α角在辨识模型中的响应与其观测结果的对比Fig.3 Comparison between result of identification and observed data of attack angle

结果表明，在有噪声的情况下，普通PSO算法和DE算法仍具有辨识能力，且DE算法的辨识结果优于普通PSO算法的辨识结果.在标准差为8%的白噪声干扰下，DE算法的辨识结果中除了CLδe的值差异较大之外，其他参数值的误差均比较小.将该组参数的辨识结果代入仿真系统，取攻角α的响应与其在真实参数值仿真系统进行仿真的观测值进行比较，如图3所示,结果显示两条曲线十分接近，可以认为DE算法的辨识结果是可靠的.

4 结论与分析

本文采用某型飞机刚体运动的6自由度非线性动力学模型，基于最小二乘法、普通PSO算法和DE算法，建立了用于辨识飞机气动力参数的辨识系统，定量分析了3种辨识方法的辨识能力，着重分析和比较了普通PSO算法和DE算法两种辨识方法在该型飞机气动力参数辨识过程中的收敛能力和鲁棒性能.

3种辨识方法的参数辨识结果显示该型飞机的气动力参数能够被精确辨识.其中，普通PSO算法和DE算法的辨识精度随着迭代次数的增加而不断提高，与给定的真实值越来越接近.迭代次数达到200时，DE算法的辨识结果基本与真实值一致，而普通PSO算法的辨识结果仍有一定偏差，说明对于该型飞机的气动力参数辨识，DE算法的收敛速度优于普通PSO算法.

普通PSO算法和DE算法在观测信号被叠加标准差为2%，5%和8%的白噪声的情况下仍然具有较高的辨识精度，表明这两种算法均具有较强的抗干扰能力.从辨识结果可以看出，DE算法的辨识误差整体小于普通PSO算法的辨识误差，表明对于该型飞机的气动力参数辨识，DE算法比普通PSO算法具有更强的鲁棒性.

在利用普通PSO算法和DE算法辨识气动力参数时，每个个体最多具有5个维度，在寻优范围内随机分布,无需设定其初始值.本文中待辨识气动力参数值的寻优范围设为[-5，0]或[0，5]，寻优结果均比较理想，体现了此类智能算法的全局寻优能力.相比于传统的梯度类算法，智能算法能够有效避免由于初值设置不合理所导致的寻优结果陷入局部最优的情况，辨识精度能够随着迭代次数的增加而提高，增强了辨识结果的可靠性.但由于随着迭代次数的增加计算量也将大大增加，所以智能算法对计算机硬件要求较高.

[1] CHEN S,BILLINGS S A,LUO W.Orthogonal least squares methods and their application to non-linear system identification [J].InternationalJournalofControl,2007,50(5)：1873-1896.

[2] 蔡金狮.飞行器系统辨识 [M].北京：宇航出版社，1995.

[3] 宋屹旻.采用有约束最小二乘辨识飞行器气动参数 [J].导弹与航天运载技术，2014(2)：1-2.

[4] 张天姣，汪清，何开锋.粒子群算法在气动力参数辨识中的应用 [J].空气动力学学报，2010,28(6)：633-638.

[5] 王锟，韩华亭，李小兵.遗传算法在导弹气动参数辨识中的应用 [J].航空兵器,2007(5)：3-6.

[6] JIANG T,LI J,HUANG K.Longitudinal parameter identification of a small unmanned aerial vehicle based on modified particle swarm optimization [J].ChineseJournalofAeronautics,2015,28(3)：865-873.

[7] STORN R,PRICE K.Differential evolution：A simple and efficient adaptive scheme for global optimization over continuous spaces [J].JournalofGlobalOptimization,1995,23(4)：341-359.

[8] URSEM R K,VADSTRUP P.Parameter identification of induction motors using differential evolution [C].Canberra,Australia：Proceedings of the IEEE Congress on Evolutionary Computation(CEC 2003),2003,2：790-796.

[9] HO W H,CHOU J H,GUO C Y.Parameter identification of chaotic systems using improved differential evolution algorithm [J].NonlinearDynamics,2010,61(1)：29-41.

ApplicationofDifferentialEvolutionAlgorithmforAerodynamicParameterIdentification

JIANZhaosheng,AIJianliang

(DepartmentofAeronauticsandAstronautics,FudanUniversity,Shanghai200433,China)

Differential Evolution(DE) algorithm is a new heuristic algorithm,compared to gradient-based methods including maximum likelihood estimation and least squares method,it does not require for the optimization problem to be differentiable,and has strong global search ability.A simulation for an airplane with given aerodynamic parameters as the true values is conducted,its input data and output data collected then are used to identify the aerodynamic parameters of the airplane.Among that the least squares method,basic Particle Swam Optimization(PSO)algorithm and DE algorithm are applied.The identification results show that the mathematical model is correct,and aerodynamic parameters can be identified accurately.When added with different strength of white noise,the identification results are correct overall.In the meantime,the results show that,in this case,DE algorithm converges faster than basic PSO algorithm does and its results are more accurate than results with basic PSO algorithm.

aerodynamic parameter identification; differential evolution algorithm; particle swarm optimization; nonlinear system identification

0427-7104(2017)05-0545-06

2016-06-07

简兆圣(1991—)，男，硕士研究生；艾剑良，男，教授，通信联系人，E-mail：aijl@fudan.edu.cn.

V249.4

A