发电机气隙静偏心故障前后定子绕组电磁力的对比分析

何玉灵， 孟庆发， 仲 昊， 蒋宏春

(华北电力大学 能源动力与机械工程学院，河北 保定 071003)

发电机气隙静偏心故障前后定子绕组电磁力的对比分析

何玉灵， 孟庆发， 仲 昊， 蒋宏春

(华北电力大学 能源动力与机械工程学院，河北 保定 071003)

以QFSN-600-2YHG型汽轮发电机在气隙静偏心故障前后的定子绕组电磁力为研究对象，通过定性理论解析和定量仿真计算分别进行对比研究，获取了定子绕组电磁力在故障前后的变化规律。首先通过推导正常运行以及气隙静偏心故障下的气隙磁密表达式，得到了故障前后定子绕组电磁力的解析表达式，然后利用有限元软件Ansoft对静偏心故障前后的电磁力进行定量仿真计算，最终得出气隙静偏心故障前后的定子绕组电磁力的力学激励特性。研究结果表明：汽轮发电机静偏心前后气隙磁密中只包含奇次谐波成分，其中以基波磁密为主；单根定子绕组电磁力均呈现出近似频率为2ω的余弦函数曲线，且部分定子绕组电磁力的峰值在静偏心故障前后出现了较大差异；定子绕组电磁力只包含直流成分和偶次谐波成分，其中以直流分量及二次谐波成分为主；所有定子绕组电磁力的瞬时值呈现出一个近似2个周期的余弦函数曲线。

汽轮发电机； 气隙静偏心； 定子绕组电磁力； Ansoft

0 引 言

气隙静偏心故障是发电机运行过程中一种常见的机械故障。定子中心与转子旋转中心不重合，转子偏离了原始的位置，产生偏心现象，这种现象的产生原因可能是加工和装配出现了误差。汽轮发电机存在气隙静偏心故障将会引起磁场发生畸变，导致气隙磁密发生变化，进而引起定子绕组电磁力发生变化，最终导致定子及定子绕组的振动加剧，甚至破坏[1]。因此，对发电机气隙静偏心故障前后定子绕组电磁力的力学激励特性进行比较分析，进而获取定子绕组在故障前后的力学响应特性，从而为此类故障的识别与绝缘的磨损监测提供依据显得尤为重要。

在发电机气隙偏心故障方面，文献[2-5]分析了偏心故障下的单位面积气隙磁导以及气隙磁密的计算方法，气隙偏心只影响单位面积气隙磁导，对气隙磁势不产生影响，为本文进行电磁力的理论推导奠定了基础。文献[6-8]得到了定子匝间短路和气隙偏心复合故障下定子电流的谐波成分，并分析了多工况背景下汽轮发电机的不平衡电磁力。在发电机定转子振动特性方面，文献[9-13]研究了发电机气隙偏心时转子的振动特性以及转子绕组的变形、应变和应力的关系，同时得到了故障特征频率幅值和偏心度之间的关系，进而推测偏心程度，文献[14]通过定性推导和实验验证分析了气隙偏心故障对汽轮发电机定转子径向振动特性的影响。在发电机建立模型方面，文献[15]提出了一种应用 ANSYS 软件实现大型水轮发电机转子偏心磁场有限元计算的方法。文献[16]建立了水轮发电机的二维有限元模型，并求解得到了静偏心和动偏心状态下的不平衡磁拉力。以上研究为本文对气隙静偏心情况下定子绕组电磁力进行仿真分析提供了参照。

本文以QFSN-600-2YHG型汽轮发电机为研究对象，采用定性理论解析和定量仿真分析相结合的研究方法，通过对比分析，得到了静偏心前后气隙磁密和定子绕组电磁力的谐波成分以及单根绕组电磁力峰值曲线和所有绕组电磁力瞬时值曲线。可以对研究定子绕组振动的成因提供参考。

1 发电机定子绕组电磁力计算模型

本文以QFSN-600-2YHG型汽轮发电机为研究对象。其主要参数如表1所示。

表1 QFSN-600-2YHG型汽轮发电机参数

定子绕组分为上层绕组和下层绕组两层，上层绕组距离气隙较近，下层绕组距离气隙相对较远。每层有42根绕组。为了便于分析，对定子绕组进行编号，其位置可根据周向角αm确定。如图1所示，定子绕组由1号绕组开始，沿逆时针方向分别为1至42号绕组。每根定子绕组的位置可表示为

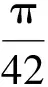
(1)

定子三相绕组结构完全相同，每相间隔为120度，定子每相绕组由两条支路组成，两支路并联，每相每条支路由7匝线圈串联组成。一个上层绕组和一个下层绕组在定子端部连接，形成一匝线圈，每条支路线圈内的电流相同。

图1 定子及定子绕组二维截面示意图 Fig.1 Schematic diagram of stator and stator windings

2 发电机定子绕组电磁力的定性理论解析

2.1发电机定转子间气隙磁密

发电机气隙磁势乘以单位面积气隙磁导得到定转子间的气隙磁密。气隙静偏心仅对单位面积气隙磁导产生影响。气隙静偏心示意图如图2所示。

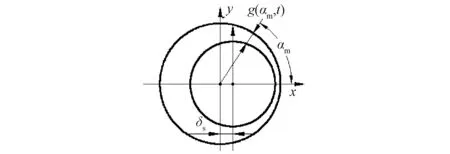
图2 气隙静偏心示意图 Fig.2 Schematic diagram of air gap static eccentricity

气隙静偏心故障下气隙的表达式：

g(αm,t)=g0(1-δscosαm)

(2)

式中：g0为平均气隙；δs为相对静偏心值，αm为发电机的机械角，以定转子最小气隙处为αm起始点。

气隙磁势可表示为

(3)

式中：Fr为主磁势(转子励磁绕组所产生的磁势)，Fs为电枢反应磁势(定子绕组所产生的磁势)，F1为合成磁势；Ψ为发电机内功角。

(4)

正常情况下，单位面积磁导的表达式：

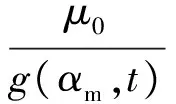
(5)

式中：Λ0为气隙磁导的常量。

气隙静偏心故障下，单位面积磁导的表达式：

(6)

忽略二次以上高次谐波，气隙静偏心故障后，单位面积磁导表达式可简化为

Λ(αm,t)≈Λ0(1+0.5δs2+δscosαm+0.5δs2cos2αm)

(7)

正常情况下，气隙磁密的表达式：

(8)

气隙静偏心故障下，气隙磁密的表达式：

(9)

气隙磁密的表达式(8)和(9)为时空函数，即其中既有时间变量又有空间变量，气隙磁密同时随着时间和空间位置的改变而变化。上两式只对发电机气隙磁密中只含波时进行的理论推导。实际上发电机气隙磁密还存在3，5，7，……奇次谐波成分，由分析可知，气隙静偏心前后磁密中只包含奇次谐波成分，其中以基波磁密为主，各高次谐波磁密的计算方法和上述方法相同。

2.2气隙静偏心前后定子绕组电磁力

由电磁感应定律可得定子绕组电磁力表达式：

F(αm,t)=B(αm,t)Il

(10)

式中：l为定子绕组切割磁感线长度。由欧姆定理可得感应电流表达式：

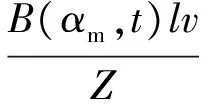
(11)

式中：v为定子绕组切割磁感线速度；Z为定子绕组的电抗。

最终可得单根定子绕组电磁力表达式：

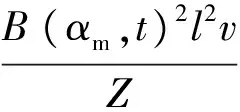
(12)

正常情况下，单根定子绕组电磁力可表示为

(13)

气隙静偏心故障下，单根定子绕组电磁力可表示为

(14)

图4 模型外电路Fig.4 External circuit of model

通过对比式(13)和(14)，当分析单根定子绕组随时间变化的电磁力时。可在m中任取一值确定周向角αm的值，然后分别代入式(13)和(14)，随着时间变化，每根定子绕组电磁力均呈现出近似频率为2ω的余弦函数曲线规律，m代入任意给定值，气隙静偏心前后每根定子绕组电磁力均有相似的变化规律，只是各绕组电磁力达到峰值的时间会有所差别。实际上发电机气隙磁密还包含3，5，7，……次谐波成分，由分析可知，定子绕组电磁力还包含4，6，8，……次谐波成分，各高次电磁力的计算方法和上述方法相同。气隙静偏心前后定子绕组电磁力只包含直流分量和偶次谐波成分，其中以直流分量及二次谐波成分为主。另外，若把时间变量t看成一个定量，式(13)和(14)将变成一个空间函数，在任一时刻，所有定子绕组电磁力的瞬时值呈现出一个近似2个周期的余弦函数曲线规律，气隙静偏心前后各定子绕组电磁力有相同的变化规律，只是故障前后各个绕组的电磁力的峰值会有所变化。

3 发电机定子绕组电磁力的定量仿真分析

3.1发电机模型的建立

根据表1中的参数，通过电磁仿真软件Ansoft建立发电机的二维物理模型。把正常物理模型中的定子铁心及定子绕组以及求解边界移动气隙的30%便可得到如图3(b)所示静偏心故障下发电机二维物理模型，外电路不需要更改。本文设置最小气隙处为发电机最右侧。模型对应的外电路如图4所示。

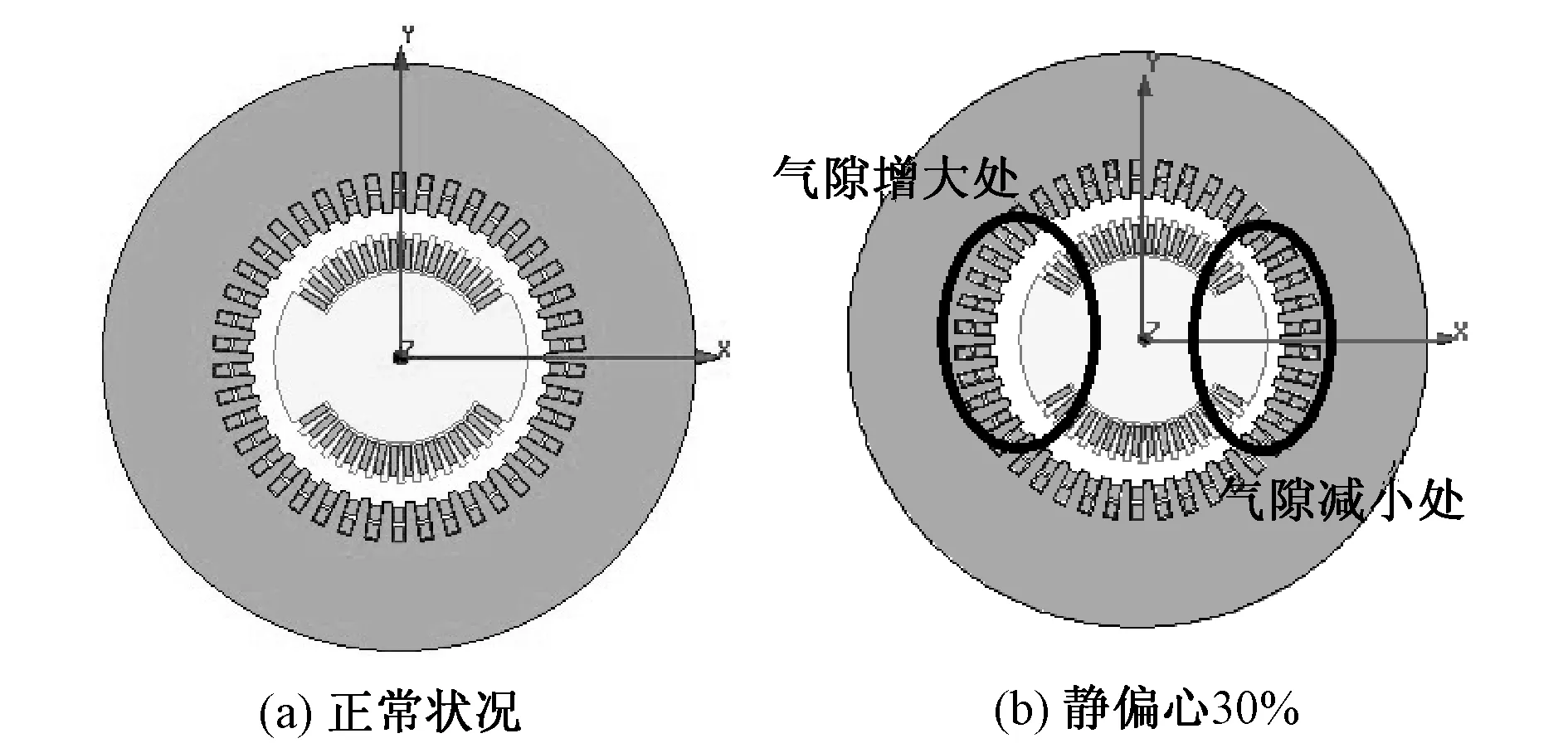
图3 发电机二维物理求解模型Fig.3 2-D physical solution model of generator

3.2发电机定转子间气隙磁密仿真分析

对上述发电机的两个二维物理求解模型进行求解，在求解时设置求解步长为0.000 1 s，求解时长为0.08 s，即为4个周期。在转子与定子间的气隙设置一路径，求得某一时刻下该路径上的磁密即为气隙整周磁密，如图5(a)所示。在最大气隙处(为了研究气隙磁密的谐波成分，随机选取气隙最左侧位置)设置一点，得到这一点随时间变化的气隙磁密，如图5(b)所示。对稳定后的时变气隙磁密做快速傅里叶变换，得到气隙磁密的谐波成分，如图5(c)所示。

图5 气隙磁密的定量仿真 Fig.5 Quantitative simulation of air gap flux density

静偏心前后，整周气隙磁密近似为余弦曲线，其为空间函数，其数值随着空间位置的改变而变化。而某一点处随时间变化的气隙磁密也近似为余弦曲线，其为时间函数，其数值随着时间变化而改变。分析气隙磁密的谐波成分发现，气隙磁密只包含奇数次谐波成分，其中以基波为主要成分(以电机的转频和输出电频率50 Hz为基波频率)。静偏心后没有新的谐波成分出现，这与上述理论分析吻合。

3.3发电机定子绕组电磁力的频域图和时域图

3.3.1 气隙静偏心前后定子绕组电磁力时域图

对上述发电机的两个二维物理求解模型求解定子绕组电磁力。本文对定子绕组的电磁力大小进行分析，暂不考虑电磁力的方向，所有电磁力均取绝对值。以图3(a)所示坐标系为参考坐标系，坐标系与定子保持相对静止。数值求解得到每根定子绕组随时间变化的电磁力，由于各定子绕组电磁力有着相似的变化规律，取上层1，5，9号绕组电磁力为例进行分析，得到气隙静偏心前后定子绕组电磁力的时域图，如图6所示。

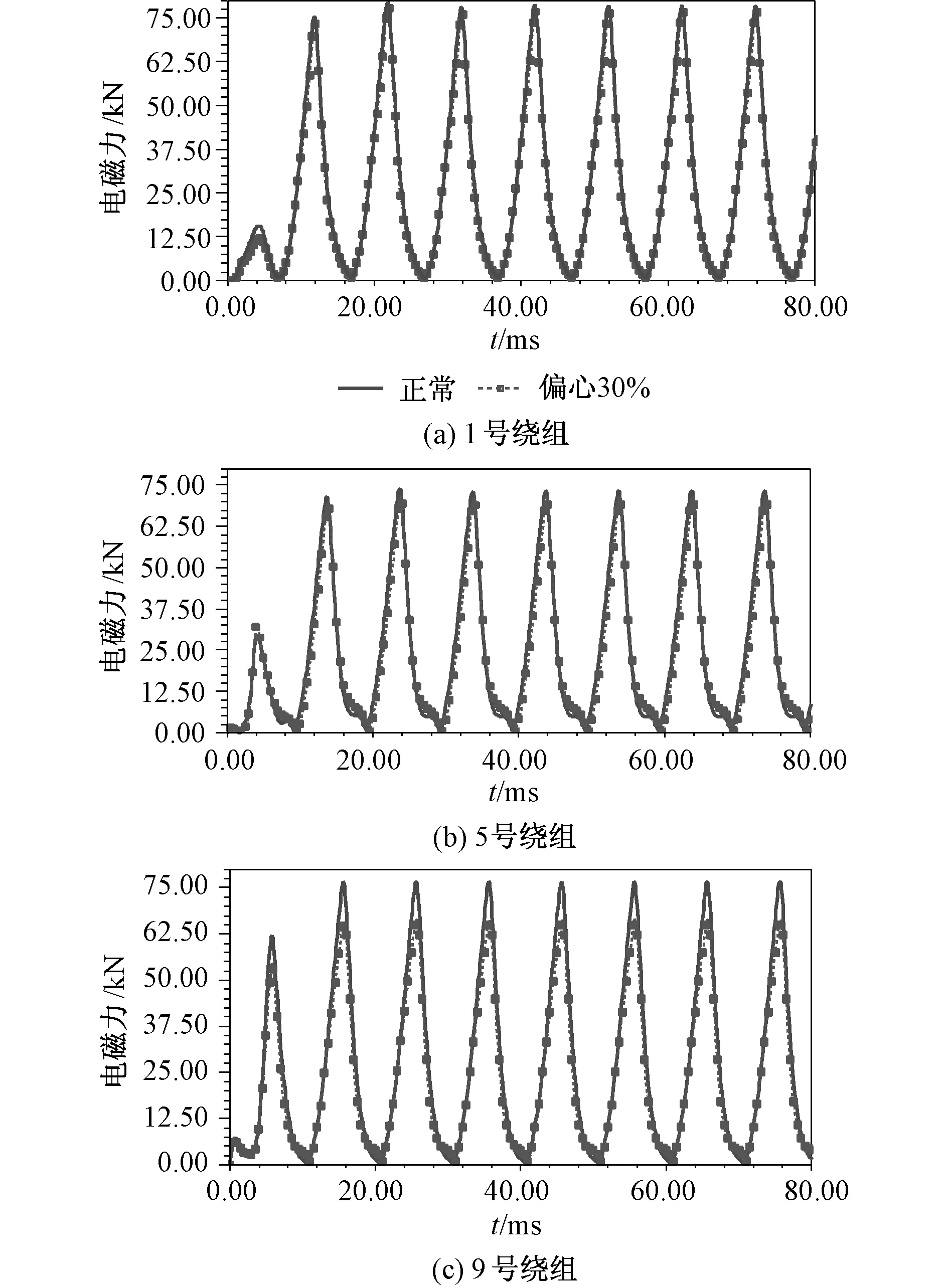
图6 电磁力时域图 Fig.6 Time domain diagram of electromagnetic force

通过对比图6可知，随着时间的变化，每根定子绕组电磁力呈现出近似频率为2ω的余弦函数曲线规律。气隙静偏心前后定子绕组上层1，5，9号绕组电磁力峰值变化程度不同，1，5号绕组电磁力峰值变化不大，9号绕组电磁力峰值出现了较大的变化。

统计气隙静偏心前后所有定子绕组电磁力峰值发现，有部分绕组电磁力峰值出现了较大的变化，如图7所示。

图7 所有绕组电磁力峰值曲线图 Fig.7 Peak of electromagnetic force of all windings

由图7可知，正常情况下，每7匝绕组电磁力有着相似的变化趋势，因为这7匝正好是一相绕组中的一个支路，各支路间绕组的电磁力变化趋势相似。实际上定子绕组每根线棒的电流与气隙磁密存在相位差(反映在相量图中为电流I与电势E0的夹角)，静偏心故障前后气隙磁密发生变化，同时各支路电流发生变化，导致各定子绕组之间电磁力峰值存在差异，部分绕组电磁力峰值增大，部分绕组电磁力峰值减小。

3.3.2 气隙静偏心前后定子绕组电磁力频域图

对稳定后电磁力进行傅里叶变换分析其中的谐波成分，得到气隙静偏心前后定子绕组电磁力频域图，如图8～图10所示。

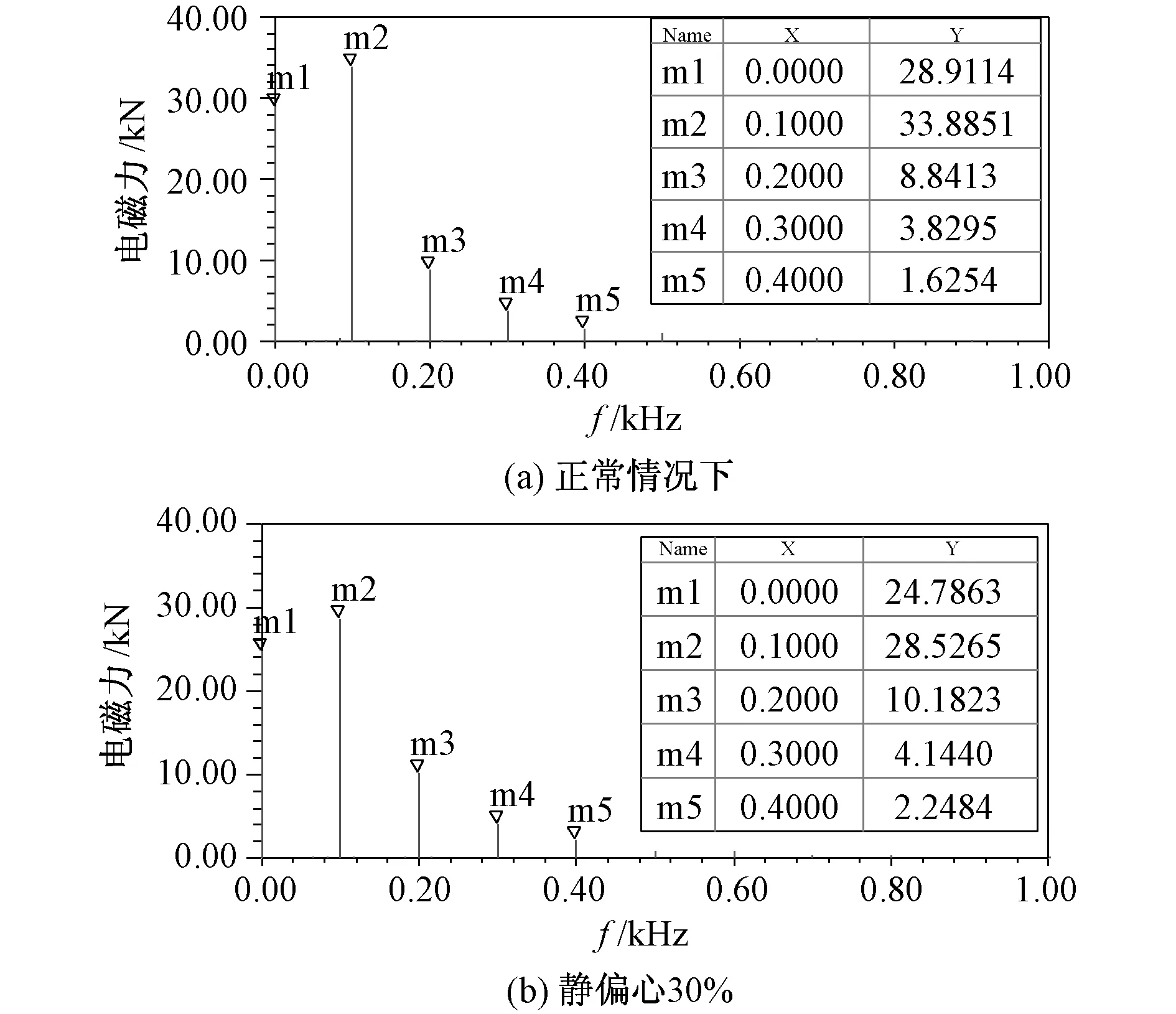
图8 1号绕组电磁力频域图Fig.8 Frequency domain diagram of electromagnetic force of No.1 winding

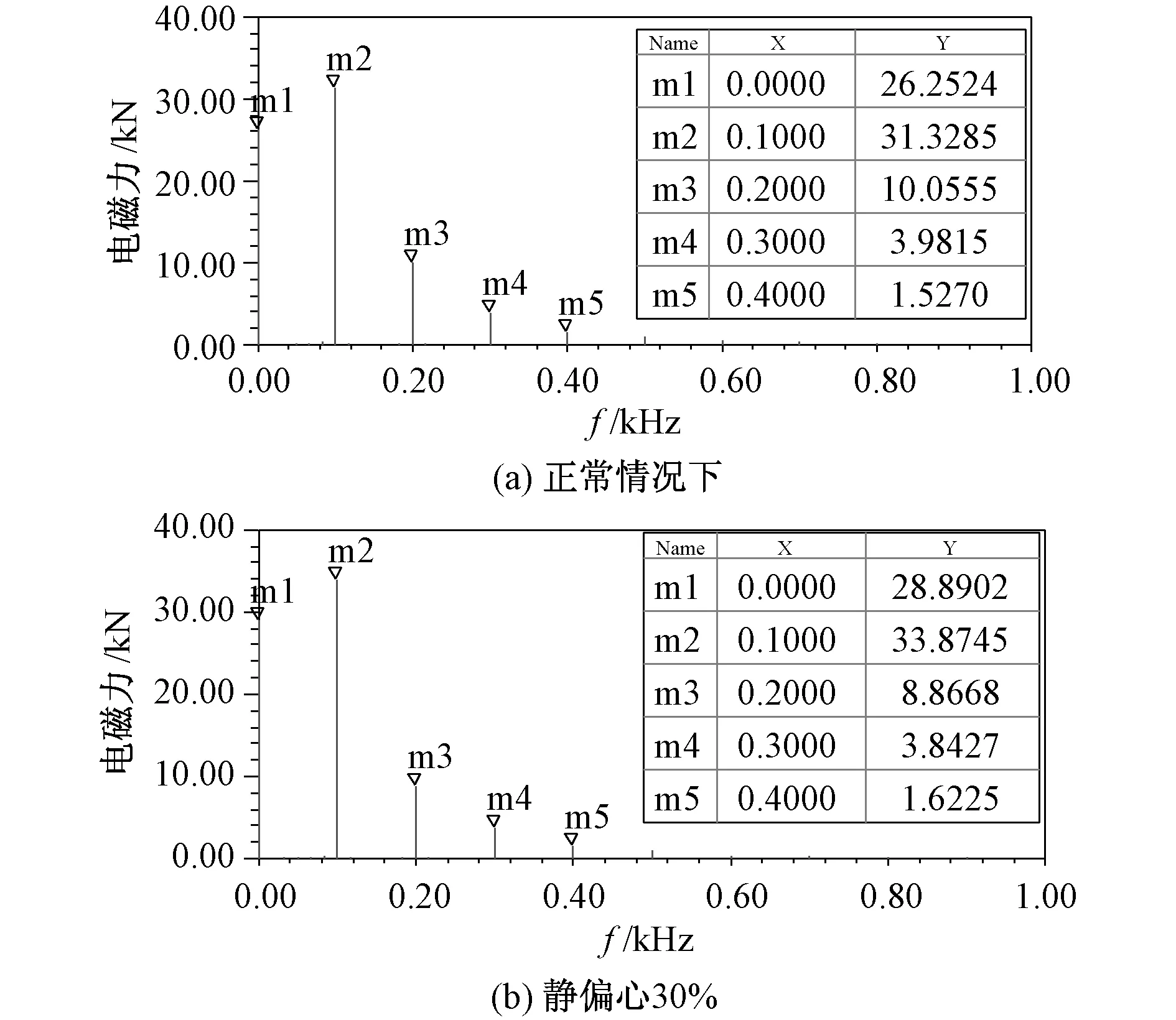
图9 5号绕组电磁力频域图Fig.9 Spectrum of electromagnetic force of No.5 winding

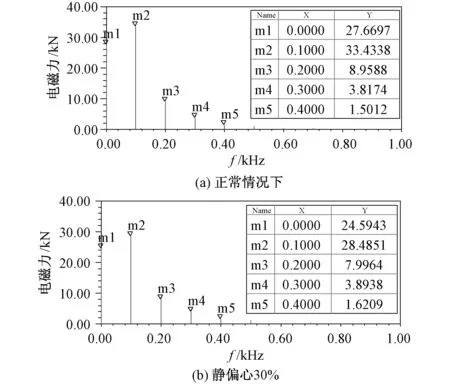
图10 9号绕组电磁力频域图Fig.10 Spectrum of electromagnetic force of No.9 winding

通过对比图8～图10可知，气隙静偏心前后定子绕组电磁力只包含直流成分和偶次谐波成分，其中以直流分量和二次谐波成分为主。定子绕组上层1，5，9号绕组电磁力变化情况不同，静偏心后1号绕组电磁力幅值减小，5号绕组电磁力幅值增大，9号绕组电磁力幅值减小。定子绕组电磁力的这种特征会导致定子绕组发生偶数倍频的振动，这种振动可能导致定子绕组的绝缘损伤以及定子振动。

为了研究发电机气隙静偏心前后所有定子绕组某一时刻电磁力瞬时值的差异性，任取一稳定运转的时刻对电磁力数值进行统计，同样，不考虑定子绕组受力方向，所有电磁力均取绝对值，最终得到某一时刻定子上下层绕组电磁力瞬时值，如图11所示。

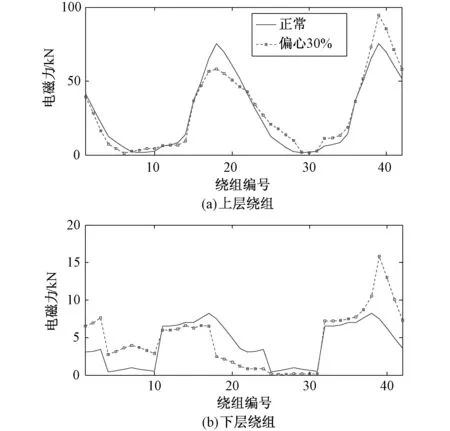
图11 某一时刻所有定子绕组电磁力瞬时值曲线图Fig.11 Instantaneous value curve of all the stator winding electromagnetic force at a certain moment

由图11可以看出，气隙静偏心前后，在某一时刻所有定子绕组电磁力在整个圆周内基本呈现出近似2个周期的余弦曲线规律，且定子绕组电磁力瞬时值的大小在静偏心故障前后产生了较大差异。

4 结 论

本文运用定性与定量相结合的研究方法，通过对汽轮发电机气隙静偏心故障前后的定子绕组电磁力的比较分析，得出以下结论：

(1)汽轮发电机气隙磁密中只包含奇次谐波成分，并且以基波磁密为主。

(2)考虑单根定子绕组电磁力的变化情况，汽轮发电机气隙静偏心前后每根定子绕组电磁力均呈现出近似频率为2ω的余弦函数曲线分布，且部分定子绕组电磁力的峰值在静偏心故障前后出现了较大差异。

(3)汽轮发电机气隙静偏心前后，定子绕组电磁力只包含直流分量和偶次谐波成分，其中以二次谐波成分为主，且部分绕组电磁力幅值增大，部分绕组电磁力幅值减小。

(4)气隙静偏心前后，在某一时刻所有定子绕组电磁力在整个圆周内基本呈现出近似2个周期的余弦曲线规律，且定子绕组电磁力瞬时值的大小在静偏心故障前后产生了较大差异。

[1] 闫雪超. 大型汽轮发电机转子偏心磁场分析与电磁力计算[D].哈尔滨：哈尔滨理工大学，2013.

[2] 何玉灵. 汽轮发电机气隙偏心故障分析与诊断方法研究[D].保定：华北电力大学，2009.

[3] 何玉灵. 发电机气隙偏心与绕组短路复合故障的机电特性分析[D].北京：华北电力大学，2012.

[4] 柯孟强. 发电机气隙偏心与转子短路复合故障下磁拉力特性分析[D].保定：华北电力大学，2016.

[5] 毛可意. 大型汽轮发电机转子偏心故障动态分析[D].哈尔滨：哈尔滨理工大学，2015.

[6] XIAO Z, FANG H. Stator Winding Inter-Turn Short Circuit and Rotor Eccentricity Diagnosis of Permanent Magnet Synchronous Generator[C]. International Conference on Control, Automation and Systems Engineering, Singapore, 2011:1-4.

[7] 冯文宗. 多工况背景下汽轮发电机不平衡电磁力的研究[D].保定：华北电力大学，2015.

[8] 李扬,郝亮亮,孙宇光,等. 隐极同步发电机转子匝间短路时转子不平衡磁拉力特征分析[J]. 电力系统自动化,2016,40(3):81-89.

[9] 万书亭. 基于机电综合特征的发电机转子故障诊断系统的研究[J]. 华北电力大学学报(自然科学版),2007,34(6):28-31.

[10] 武玉才,李永刚,李和明,等. 机电复合故障下汽轮发电机转子振动特性分析[J].高电压技术,2010，36(11):2687-2692.

[11] 蒋宏春,伍世良,何玉灵,等. 气隙静态偏心故障下汽轮发电机励磁绕组受载及其力学响应分析[J]. 电机与控制应用,2016,43(8):46-50.

[12] 常悦. 基于振动信号分析的感应电机气隙偏心故障诊断的研究[D].杭州：浙江大学，2016.

[13] 张金华,陈永庚,彭涵,等. 水轮发电机组转子轻微偏心时的电磁性能分析[J]. 水电与新能源,2015,(6): 20-24.

[14] 万书亭,李和明,李永刚. 气隙偏心对汽轮发电机定转子振动特性的影响[J]. 振动与冲击,2005,24(6): 21-23.

[15] 诸嘉慧,邱阿瑞. 大型水轮发电机转子偏心磁场的计算[J]. 大电机技术,2007,(3):1-4.

[16] DIRANI H C, MERKHOUF A, GIROUX A M, et al. Study of the impact of eccentricity in large synchronous generator with finite elements[C]. International Conference on Electrical Machines, IEEE, Berlin, 2014:277-282.

Comparative Analysis of Stator Winding Electromagnetic Force Before and After Static Air-gap Eccentricity Fault of Generator

HE Yuling, MENG Qingfa, ZHONG Hao, JIANG Hongchun

(School of Energy Power and Mechanical Engineering, North China Electric Power University, Baoding 071003,China)

The stator windings of domestic QFSN-600-2YHG turbo-generator before and after the static air-gap eccentric fault are studied. The change law of electromagnetic force of stator winding before and after fault is obtained with the comparison of qualitative theoretical analysis and quantitative simulation calculation. This paper firstly deduces the expression of air-gap magnetic flux density under normal operation and air-gap static eccentric fault. On this basis, the analytical expressions of stator winding electromagnetic force before and after the fault are gained. Then the finite element software Ansoft is used to simulate the electromagnetic force under the two situations. Finally, the mechanical excitation characteristics of stator winding electromagnetic force before and after the air-gap static eccentric fault are acquired. The results show that the air-gap magnetic density of turbo-generator only contains odd harmonic, and the fundamental magnetic density is the main component. The peak value of the electromagnetic force of all the stator windings presents a cosine function curve with an approximate frequency of 2ω. And there is a big difference between the peak value of the electromagnetic force of the stator winding before and after the static eccentricity fault. While the electromagnetic force of the stator winding only contains the DC component and the even harmonic component. The DC component and the second harmonic are the main components. The instantaneous values of the electromagnetic force of all the stator windings present a cosine curve with approximate 2 cycles.

turbo-generator; static air-gap eccentricity; stator winding electromagnetic force; Ansoft

10.3969/j.ISSN.1007-2691.2017.05.11

TM31

A

1007-2691(2017)05-0074-07

2017-02-22.

国家自然科学基金资助项目(51307058)；河北自然科学基金资助项目(E2015502013)；中央高校科研业务费专项目基金资助项目(2015ZD27).

何玉灵(1984-)，男，副教授，研究方向为电站设备状态监测、控制与节能；孟庆发(1992-)，男，硕士研究生，研究方向为发电机的状态监测与故障诊断；仲昊(1990-)，男，硕士研究生，研究方向为发电机的状态监测与故障诊断。