新型自适应算法在复杂遮阴条件下MPPT中的应用

盛四清， 陈玉良

(华北电力大学 电气与电子工程学院, 河北 保定 071003)

新型自适应算法在复杂遮阴条件下MPPT中的应用

盛四清， 陈玉良

(华北电力大学 电气与电子工程学院, 河北 保定 071003)

光伏阵列输出特性具有明显的非线性特征，并且当光伏阵列被部分遮挡时其输出特性出现多个峰值。传统变步长MPPT方法对均匀光照条件下的单峰值特性寻优问题取得了良好的效果，但其在处理多峰值寻优问题时可能会失效。针对上述情况，提出了一种新型自适应变步长MPPT方法。首先建立部分遮阴情况下光伏阵列数学模型，然后根据最大功率点所在电压区间与开路电压和短路电流呈现出的特殊规律，将多峰值寻优问题转化为单峰值寻优问题。找到其所在区间后启用改进自适应算法搜索全局最大功率点，仿真结果表明该算法在无遮阴和部分遮阴情况下均能有效找到全局最大功率点。

光伏系统； 局部遮阴； 最大功率点跟踪； 自适应； 开路电压； 短路电流

0 引 言

随着社会的进步，太阳能发电已经成为我国电能的主要来源之一[1]。与传统的化石能源相比，光伏发电作为一种无污染可再生新能源具有巨大的发展前景。然而，光伏电池的输出特性随外界环境变化呈明显的非线性，并且其光电转换效率非常低。因此，最大功率点跟踪(Maximum Power Point Tracking,MPPT)技术已经成为人们研究的热点问题。

到目前为止，人们已经提出多种MPPT控制策略[2-5]。经典的方法有恒定电压法、扰动观测法[6]以及电导增量法[7]等。其中电导增量法和扰动观测法是目前应用最为广泛的两种方法。传统定步长MPPT方法在步长选取时难以解决稳态精度与瞬态响应速度之间的矛盾。因此文献[8]提出梯度式变步长MPPT策略，该方法采用定电圧斜率启动方式，将步长因子定义为前后两次功率差的比值，并且加入功率预测算法，动态性能与稳态性能都取得了良好的效果。然而，当光伏阵列发生遮阴情况时，其输出特性呈现多峰特性[9-10]，此时上述MPPT方法在寻找全局最大功率点(Global Peak,GP)时可能会失效。文献[11]提出改进型电导增量法，利用开路电压和最大功率点电压之间的近似关系来寻找最大功率点，但是该方法要搜索所有可能出现局部极值点的电压区间才能找到MPP，因此其动态响应速度较慢。论文中提出新型自适应MPPT算法，当检测到光伏阵列发生遮阴现象时，通过所提算法快速将工作点调整到最大功率点所在的电压区间，此时多峰值寻优转化为单峰值寻优问题，然后通过自适应变步长方法即可找到全局最大功率点。同时，为了避免光伏电池输出功率在最大功率点处振荡，在上述算法中加入扰动终止策略。在Matlab/Simulink中搭建仿真模型，仿真结果表明该算法在无遮阴和部分遮阴情况下均能有效找到全局最大功率点，并且能够有效防止光伏阵列输出功率在MPP处振荡，提高光伏电池输出效率。

1 部分阴影条件下光伏阵列数学模型

光伏阵列由多个光伏模块串并联构成。光伏系统在部分遮蔽条件下，被遮挡部分接收到的光照强度小于其他光伏模块，因此其输出电流较接受均匀光照部分要小很多。在串联结构中，流过每一个光伏阵列的电流是相同的，被遮挡部分需要一个反向电压以保证正常工作。被遮挡的光伏组件将被当做负载消耗其他光伏电池产生的电能，此时就会出现“热斑效应”。在实际应用中，通过并联一个旁路二极管来解决此问题。图1为m行n列光伏阵列示意图。

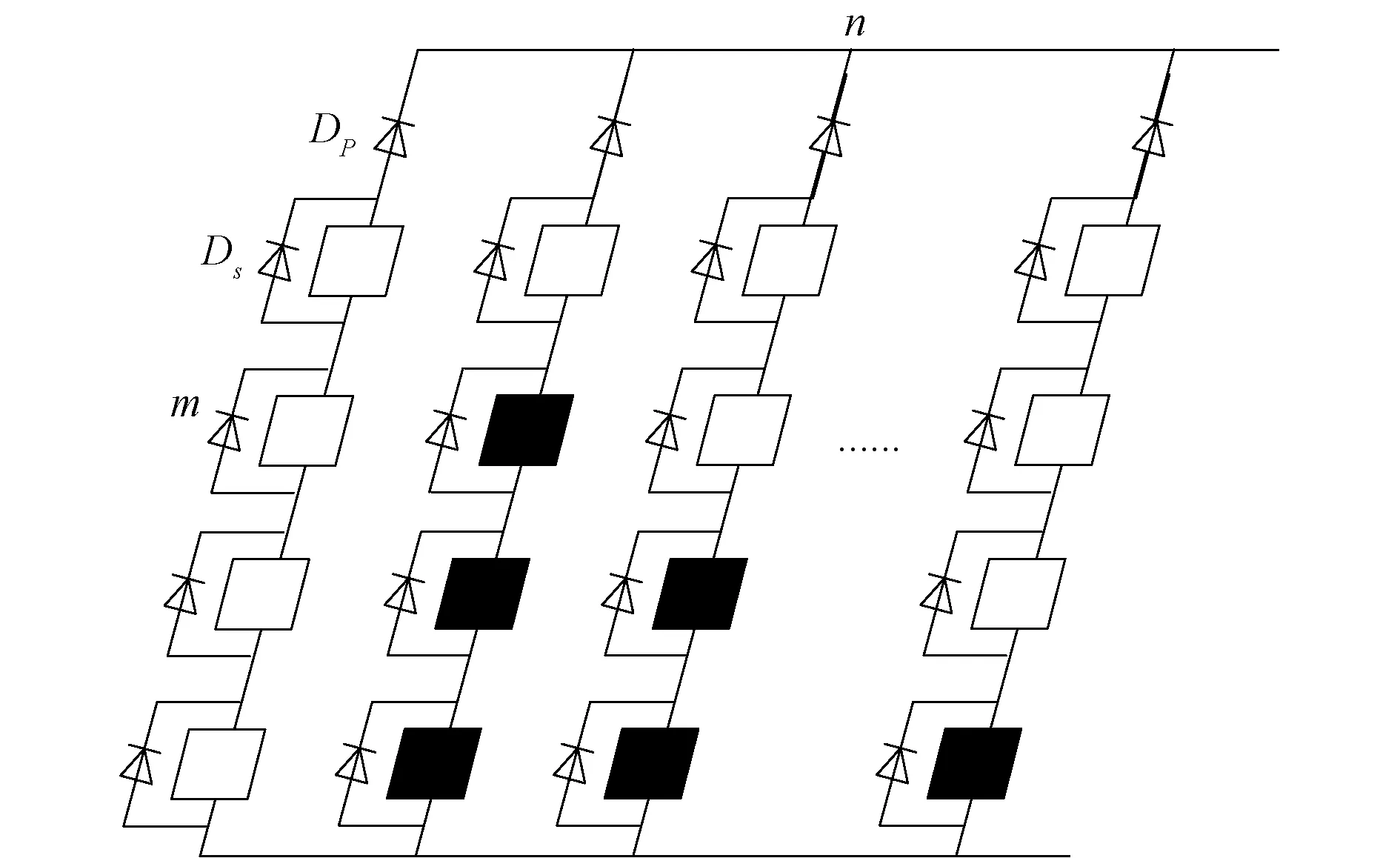
图1 光伏阵列示意图Fig.1 Schematic of photovoltaic array

假设上图中二极管具有理想二极管特性，则每个光伏阵列串联结构的数学模型[12]可以表示为

(1)

式中：Ij、Vj分别为光伏串联结构第j列的输出电流和输出电压。其中，Iij=f(Vij)为单个光伏电池输出特性关系式，其可以表示为

(2)

式中：Isc、Voc分别为标准测试条件下光伏电池短路电流和开路电压；Vm、Im分别为光伏电池最大功率点电压和电流。由图1可知，上述光伏阵列由n列光伏电池并联组成，则光伏阵列的数学模型可以被描述为

(3)

式中：I、V分别为光伏阵列输出电流和输出电压。实际上，光伏阵列由多个光伏模块组成，由于模块本身或阴影等原因，导致每个模块的输出特性各不相同，加入旁路二极管后光伏阵列输出特性曲线出现多个峰值。

2 新型自适应MPPT算法

常规变步长MPPT算法(Conventional MPPT,CMPPT)在环境光照不变的条件下具有良好的稳态精度以及响应速度，当发生局部遮挡时，光伏阵列输出特性曲线呈现多峰值特性，此时常规变步长MPPT方法在最大值寻优时可能会失效[13-14]。利用Matlab/Simulink对不同阵列在不同温度及光照下的输出特性进行仿真，归纳了光伏阵列在局部阴影条件下输出特性的变化规律。论文中提出一种先搜索全局最大值点所在区间(Global Peak Interval,GPI),然后与自适应变步长(Adaptive MPPT,AMPPT)算法相结合的MPPT算法。

2.1搜索全局最大功率点所在区间

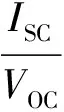
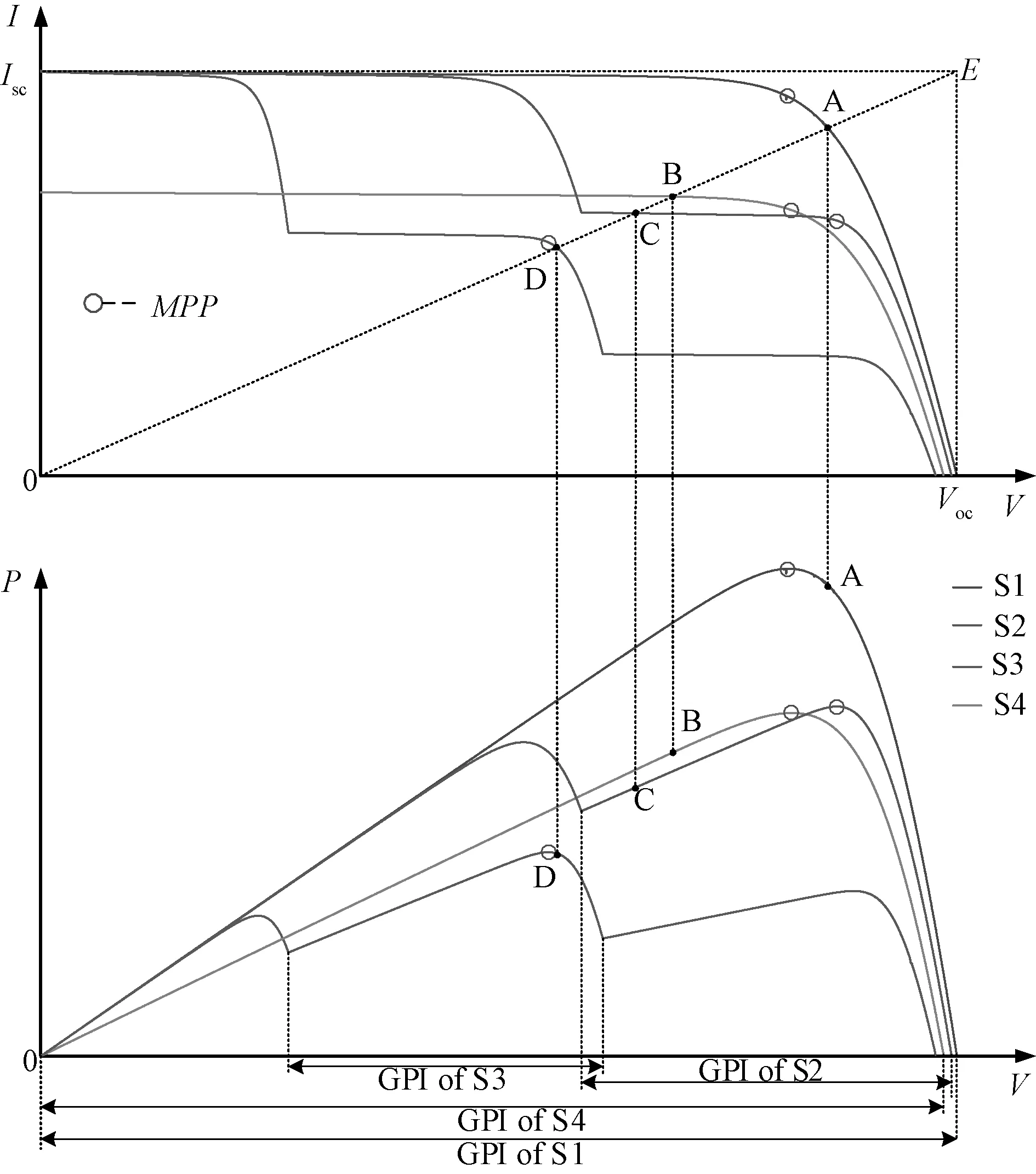
图2 GPI搜索原理图Fig.2 Search schematic of GPI

2.2算法重启条件

当光照条件为均匀光照或者发生遮蔽情况时，光伏阵列的I-V特性曲线总是呈现出单调递减特性。当MPPT算法沿着I-V特性曲线搜索全局最大值时，电压的升高伴随着电流的下降，反之亦然。当光照条件发生变化时，光伏阵列输出特性曲线也会随之发生改变。如图3所示，环境光照条件发生变化时，光伏电池I-V特性曲线由S1变为S2。若光伏阵列与恒定阻抗负载相连接，工作点由A点变为B点，此时光伏阵列的输出电压和输出电流同时减小，反之光伏电池特性曲线由S2变为S1时，其输出电压和输出电流同时增大；当光伏阵列与恒定电压负载(如DC-AC逆变器)相连接时，电压变化量ΔV几乎为0，电流变化量ΔI则非常显著。由以上分析可知，当式(4)得到满足时认为外界光照发生变化，需要重新启动上述MPPT算法。式中，ε1为电流偏差阈值。

(4)

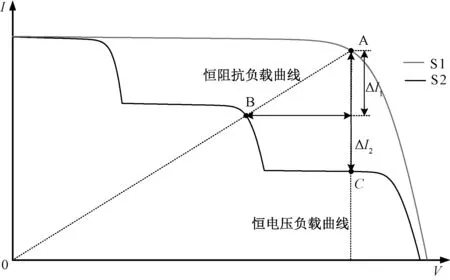
图3 算法重启条件原理图Fig.3 Schematic diagram of the algorithm restart

2.3新型自适应MPPT算法

通过式(4)检测到外界光照条件发生变化时，所提算法将工作点快速调整到V/I等于VOC/ISC的位置，此时工作点将会位于最大功率点所在的GPI。然后启动自适应变步长算法快速定位到全局最大功率点MPP。

论文中对常规变步长MPPT算法进行改进，常规变步长算法不能同时满足瞬态响应速度和稳态精度的要求，为了提高最大功率点跟踪的精确性和快速性，论文中采用新的步长因子λstep=α|ΔP|。式中，α为步长调节因子。并且为了防止在最大功率点附近振荡，设置功率偏差阈值ε3，认为当|ΔP|<ε3时达到最大功率点，停止对步长的扰动，从而有效避免输出功率在MPP附近来回振荡的现象。

图4 寻优过程原理图Fig.4 Schematic diagram of the optimization process

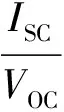
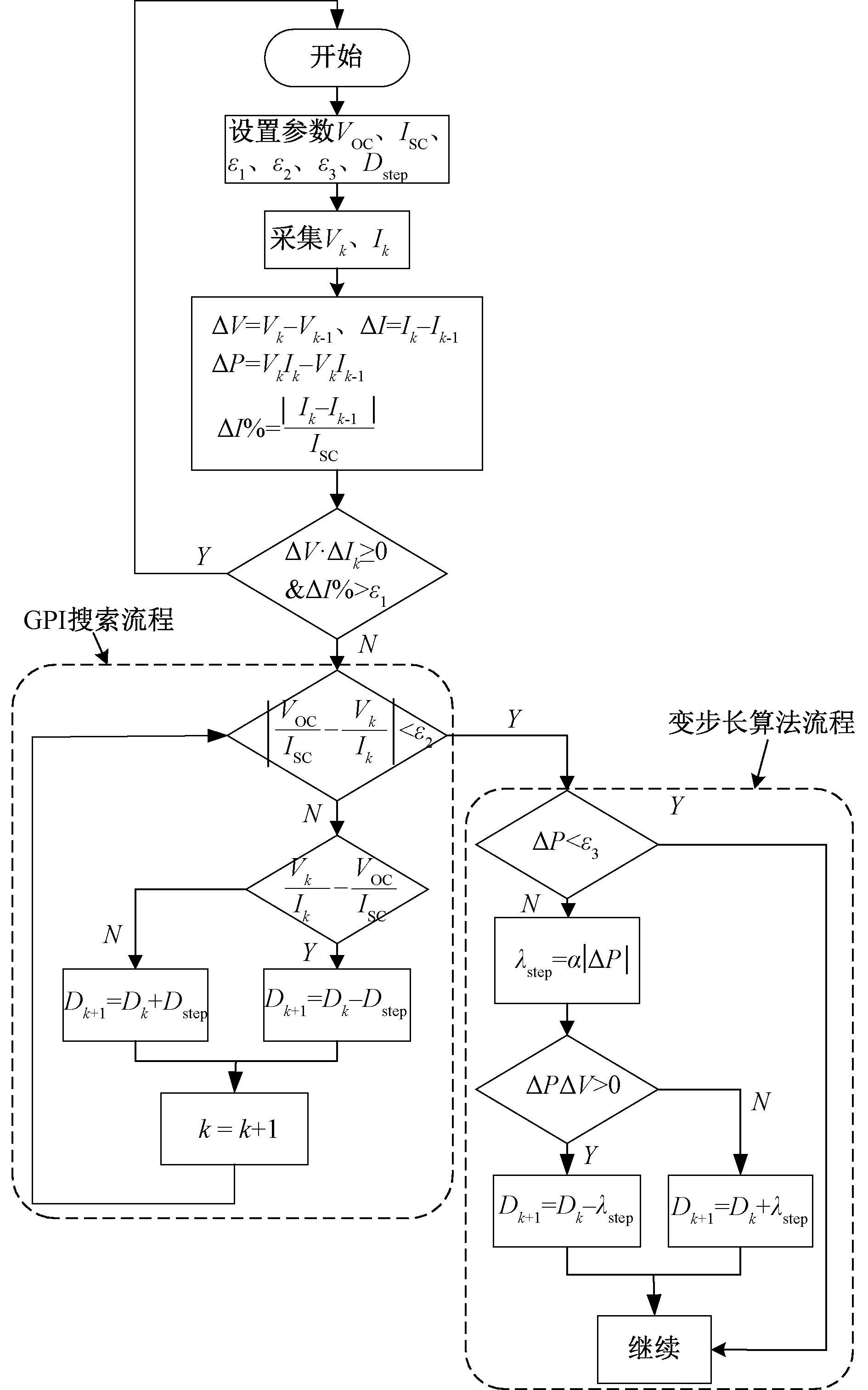
图5 MPPT算法流程图Fig.5 MPPT algorithm flow chart

3 仿真验证

根据上述算法在Matlab/Simulink中搭建仿真模型，仿真模型由光伏阵列、升压变换器、MPPT模块以及恒定负载组成。系统拓扑结构如图6所示。其中，仿真中所用光伏电池参数如表1所示。

以图7(a)所示的四种遮阴情况为例进行仿真验证。如图7(a)所示，四种遮阴情况全局最大功率点分别记为A～D。在本次仿真中，设置仿真时间为0.8 s，并且每过0.2 s对光伏阵列遮阴模式进行一次改变，光照改变的顺序为S1-S2-S3-S4。本次仿真中与上述自适应MPPT算法有关参数如表2所示。

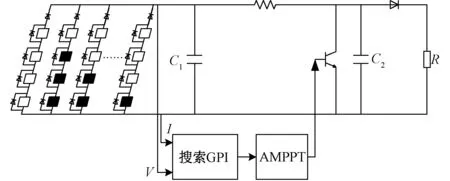
图6 仿真电路拓扑图Fig.6 Simulation circuit topology diagram

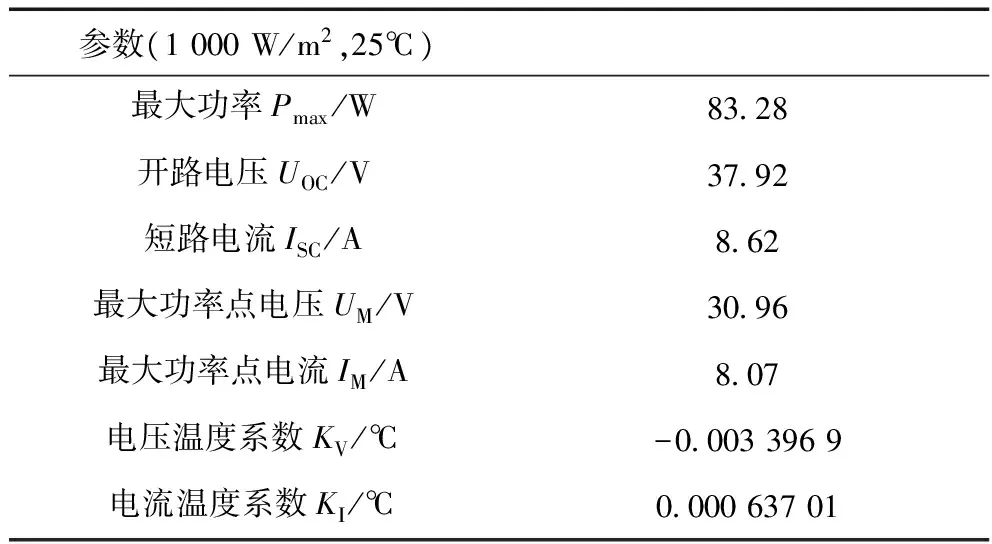
参数(1000W/m2，25℃)最大功率Pmax/W8328开路电压UOC/V3792短路电流ISC/A862最大功率点电压UM/V3096最大功率点电流IM/A807电压温度系数KV/℃-00033969电流温度系数KI/℃000063701

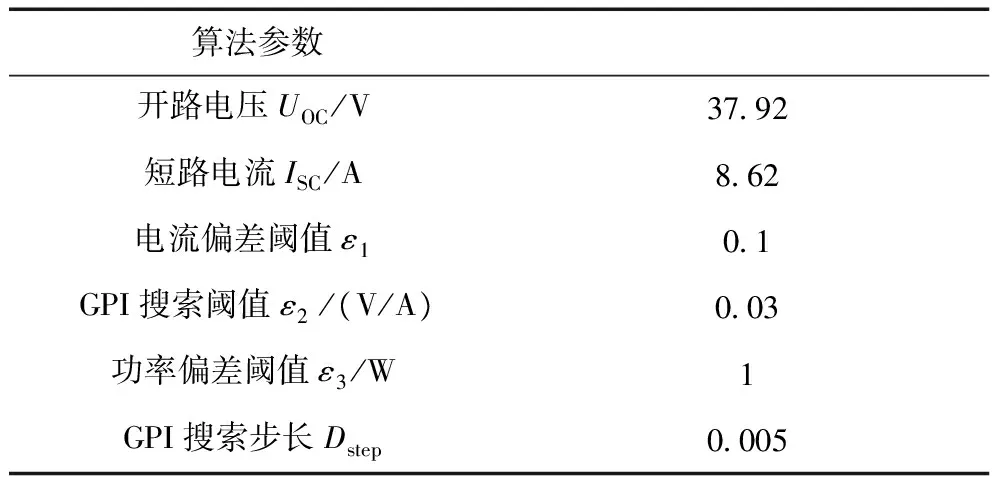
表2 自适应MPPT算法相关参数

图7(b)为采用常规变步长算法与新型自适应变步长算法光伏阵列输出功率对比图。首先，从图中可以看出在0～0.2 s以及0.6～0.8 s的时间内，光伏电池输出特性曲线为单峰值曲线，即当外界光照无阴影时，上述两种方法均能搜索到最大功率点，但所提自适应MPPT方法动态响应速度更快，并且在最大功率点时的功率输出振荡较小，稳态性能得到提高；而在0.2～0.4 s以及0.4～0.6 s时间内，光伏阵列发生遮阴情况，常规变步长MPPT方法搜索最大功率点失败，尤其是在0.4～0.6 s时间内，其输出为局部最大功率点功率，与全局最大功率点功率相比大约造成31.1%的功率损失，使得光伏阵列输出效率大幅度降低。

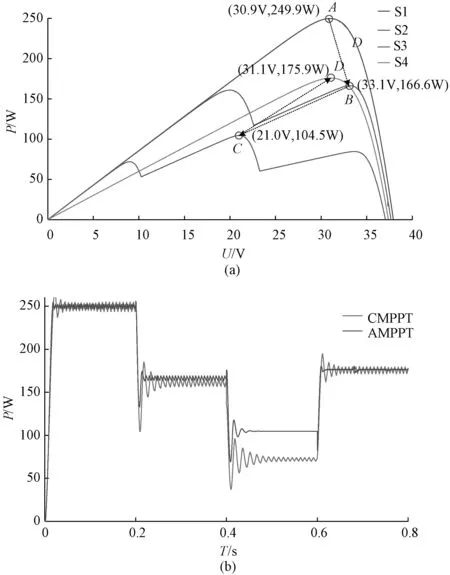
图7 输出功率对比结果Fig.7 Output power comparison results

4 结 论

本文通过分析光伏阵列在不同遮阴模式下输出特性的仿真结果发现：在光伏阵列P-V特性曲线中全局最大功率点所在区间(GPI)与光伏电池开路电压和短路电流呈现出一定规律。该规律适用于绝大多数遮阴情况，根据该规律将多峰值寻优问题转化为单峰值最优问题，然后通过改进自适应算法找到全局最优点。在Matlab/Simulink搭建仿真模型，仿真结果表明该算法在无遮阴和部分遮阴情况时均能有效找到全局最大功率点，并且能够有效防止光伏阵列输出功率在MPP处振荡，提高光伏电池输出效率。

[1] 艾欣, 韩晓男, 孙英云. 光伏发电并网及其相关技术发展现状与展望[J]. 现代电力, 2013, 30(1):1-7.

[2] 周林, 武剑, 栗秋华, 等. 光伏阵列最大功率点跟踪控制方法综述[J]. 高电压技术, 2008, 34(6):1145-1154.

[3] SUNDARESWARAN K, KUMAR V V, PALANI S. Application of a combined particle swarm optimization and perturb and observe method for MPPT in PV systems under partial shading conditions[J]. Renewable Energy, 2015, 75:308-317.

[4] 聂晓华, 赖家俊. 局部阴影下光伏阵列全局最大功率点跟踪控制方法综述[J]. 电网技术, 2014, 38(12):3279-3285.

[5] 李勇, 程汉湘, 陈杏灿, 等. 光伏电池输出特性及其最大功率跟踪研究[J]. 华北电力大学学报(自然科学版), 2017, 44(1): 70-75.

[6] 杭凤海, 杨伟, 朱文艳. 光伏系统MPPT的扰动观测法分析与改进[J]. 电力系统保护与控制, 2014，42(9):110-114.

[7] 栗晓政, 孙建平. 基于分段数值逼近的自适应步长电导增量法MPPT控制仿真[J]. 太阳能学报, 2012, 33(7):1164-1170.

[8] 陈亚爱, 周京华, 李津, 等. 梯度式变步长MPPT算法在光伏系统中的应用[J]. 中国电机工程学报, 2014, 34(19):3156-3161.

[9] 周笛青, 吴春华, 李智华, 等. 局部阴影下光伏组件建模及输出特性研究[J]. 太阳能学报, 2014, 35(11):2098-2105.

[10] 戚军, 翁国庆, 章旌红. 光伏阵列多峰最大功率点分布特点研究[J]. 电力自动化设备, 2014, 34(3):132-137.

[11] 孙博, 梅军, 郑建勇. 局部阴影条件下最大功率点跟踪改进算法[J]. 电力自动化设备, 2014, 34(1):115-119.

[12] QI J, ZHANG Y, CHEN Y. Modeling and maximum power point tracking (MPPT) method for PV array under partial shade conditions[J]. Renewable Energy, 2014, 66(3):337-345.

[13] 周天沛, 孙伟. 不规则阴影影响下光伏阵列最大功率点跟踪方法[J]. 电力系统自动化, 2015，39(10):42-49.

[14] 游国栋, 李继生, 侯勇, 等. 部分遮蔽光伏发电系统的建模及MPPT控制[J]. 电网技术, 2013, 37(11):3037-3045.

[15] 胡义华, 陈昊, 徐瑞东, 等. 阴影影响下最大功率点跟踪控制[J]. 中国电机工程学报, 2012, 32(9):14-26.

Application of New Adaptive Algorithm in MPPT Under Complex Shading Conditions

SHENG Siqing, CHEN Yuliang

(School of Electrical and Electronic Engineering, North China Electric Power University, Baoding 071003, China)

The output characteristics of the PV array are significantly non-linear, and there appear multiple peaks when the PV array is partially shaded. The conventional variable step-size MPPT method has a good effect on the optimization of the single peak value under the condition of uniform light, but it may fail when dealing with the multi peak optimization problem. Considering the above situation, this paper proposes a new adaptive variable step size MPPT method. Firstly, a mathematical model of PV array under partial shading is established, and then the multi-peak optimization problem is transformed into a single peak optimization problem based on the interval of voltage where maximum power point is located as well as the special discipline represented by open circuit voltage and short circuit current. Use the improved adaptive algorithm to search for overall maximum power point after finding the interval of the MPP. The simulation results show that the algorithm can accurately find the overall maximum power point under both none and partial shading conditions.

photovoltaic system; partial shading; maximum power point tracking; adaptive; open circuit voltage; short circuit current

10.3969/j.ISSN.1007-2691.2017.05.05

TM914

A

1007-2691(2017)05-0034-06

2017-02-26.

盛四清(1965-)，男，教授，研究方向为电力系统分析与控制；陈玉良(1993 -)，男，硕士研究生，研究方向为电力系统分析与控制。