基于机组组合的风电系统储能源功率与容量优化配置

刘永民， 夏世威， 于琳琳， 李庚银， 黄景慧

(1.国网河南省电力公司经济技术研究院，河南 郑州 450052； 2.华北电力大学 新能源电力系统国家重点实验室，北京 102206)

基于机组组合的风电系统储能源功率与容量优化配置

刘永民1， 夏世威2， 于琳琳1， 李庚银2， 黄景慧1

(1.国网河南省电力公司经济技术研究院，河南 郑州 450052； 2.华北电力大学 新能源电力系统国家重点实验室，北京 102206)

为风电系统配置合适规格的储能源，能有效抑制风电网功率波动及提高系统经济运行水平。首先分析了风电功率波动随机特征，再以机组组合问题为基础提出了兼顾储能源安装、运行日均摊费用及机组燃料期望费用的储能随机规划模型。为求解模型，进一步设计了基于点估计和并行分支定界法的综合计算方案，快速有效地确定了储能源的最优功率和容量配置。最后通过含风电的10机系统详细分析了4种不同类型储能源的经济效益，仿真结果和对比分析表明：所提出的储能随机规划模型合理，设计的综合求解方案快速有效。

风电； 概率特征； 机组组合； 储能源； 点估计； 并行分支定界法

0 引 言

可再生能源发电具有环保和可持续性等优点得到了电力界的普遍认可，目前中国正在建设含高比例可再生能源的新一代电力系统。随着可再生能源上网尤其风电并网比例提高，电网功率将呈现出更强的随机性和波动性。为有效抑制电网功率波动，配置合适规模的储能源(Energy Storage Source，ESS)显得尤其重要。

ESS配置问题在国内外得到了广泛关注。文献[1]用禁忌搜索进化算法计算了ESS的最优配置容量，分析了ESS在寿命期内为热电厂带来的经济效益。文献[2]建立了回热加热系统的质量-能量平衡方程，根据等效焓降法计算了机组凝结水系统的合理蓄能容量。文献[3]研究了以风电机组及ESS的输出功率波动标准差为指标的ESS功率和容量优化方案。文献[4]结合不同储能介质的互补平抑特性，研究了以建设和运行成本总和最小为目标的复合储能系统最优容量配置。文献[5]基于分布式能源的客户选择模型确定了ESS最优容量和运行安排，结果表明适宜容量的ESS对减少电网的年度费用非常有效。文献[6]用前馈神经网络方法预测了光伏发电曲线，再基于传统UC问题确定了联网和孤岛模式下微网ESS最佳参数，而文献[7]同样基于UC模型确定了多个质子交换膜电池的最佳容量。文献[8]基于供电可靠性建立了风光混合发电系统容量的数学模型，并用动态规划方法安排了储能的充放电计划。文献[9]利用离散傅里叶频谱分析并计及ESS充放电效率、荷电状态及新能源发电功率输出波动率约束，确定了系统所需ESS最小容量。文献[10]基于电网电能缺失总量以及瞬时功率缺失情况，用粒子群方法求解了包含超级电容器和蓄电池的混合储能系统容量，提高了系统的经济性。文献[11]分析了风电场不同周期下的预测误差，并以此为基础建立了ESS规模与风电场风能损失的效益模型，确定了ESS的额定功率和容量。文献[12]基于粒子群法、从系统频率控制的角度求解了电池储能装置的适宜容量，分析了储能对防止微网系统不稳定和解列的有效性。特别是，文献[13]对电网中含有风电的ESS进行了研究，并提出三步法来求解ESS的配置以减少输电网阻塞。文中依据多年的风电数据，以小时为单位基于传统UC模型，逐天滚动求解了大量的混合整数规划问题，确定了ESS最优容量配置和系统能量调度安排。文[13]对每一天均求解24小时的UC问题来确定ESS容量，此过程需对多年的风电数据按天滚动进行，计算过程显得繁琐，计算量大，也不便于扩展到含有更长期风电数据的储能规划问题。

本文提出了含不确定风电的电网储能随机规划模型。文中首先依据风电数据建立了风电功率的概率模型，然后提出了考虑储能安装、运行成本以及常规机组燃料费用期望值的ESS随机规划模型。为求解模型，文中引入点估计法将随机规划模型转化为具有特殊结构的UC问题，最后采用并行BB方法进行求解，从而获得储能的最优功率和容量配置。论文主要具有以下特点：

(1)区别于文献[13]基于逐天滚动UC的建模方式，本文基于长期风电数据分析并确定了风电功率的概率模型及参数，再直接将风电的概率特征考虑进储能随机规划模型。先归纳风电概率特征再提出随机规划模型的思路，简单明了，易于拓展到含有更长期风电数据的电网储能规划问题。

(2)所提的储能随机规划模型同时考虑了机组的费用期望值以及ESS的安装、运行日均摊费用，模型具有通用性和扩展性，可灵活适应于含有不同概率特征的风电等可再生能源系统的储能规划。

(3)文中提出了基于点估计和并行分支定界法的综合求解方案，可快速有效地求解ESS随机规划模型。

(4)算例仿真验证了所提模型的合理性和求解方案的有效性，并对不同种类的ESS成本效益进行了充分讨论。

1 ESS随机规划模型

本节基于UC提出ESS随机规划模型。所提模型和文献[13]均以N年为规划的时间跨度，但不同于文献[13]逐天滚动求解UC的方法，文中首先从多年的历史数据中分析风电功率出力特征，然后再基于已归纳的风电概率曲线建立ESS容量配置的随机优化模型。

1.1风电功率的概率模型建立

针对多年的风电历史数据，本文以小时为颗粒度，将每天同一小时的风电数据用直方图进行统计，再进行概率曲线拟合而得风电出力的概率曲线。以文献[14]中的2013和2014年风电数据为例，将每一天数据划分为24个时间区间，然后再将所有处于00：00至1：00的风电数据收集并用直方图绘出，得到第一小时(00：00-1：00)的风电功率分布曲线如图1所示，其符合公式(1)描述的威布尔分布，形状系数为λ=0.307和尺度参数k=1.230；采用同样的处理方法，可以依次获得1：00-24：00每小时的风电功率概率特征，其符合威布尔分布且相应参数见附录表A-1所示。

图1 00：00-1：00小时的风电功率直方图Fig.1 Histogram of wind power during hour 00：00-1：00

(1)

通过以上分析，基于风电历史数据可获得一天24小时对应的24组风电功率的威布尔分布曲线，从而可以将风电功率的概率特征方便的考虑在ESS容量随机规划模型中。另外指出，虽然基于文献[14]数据确定的风电功率为威布尔概率分布，但对于任何已知风电数据，均可以采用上述过程获得相应的概率分布(如贝塔分布)及其参数；后文所提的ESS容量配置模型及解法并不局限于威布尔分布，对其他概率分布的风电功率也具有很好的通用性。

1.2ESS规划模型

由于模型考虑了风电的随机性，UC问题对应的机组燃料费用变为不确定量，因此需将机组费用以期望值形式表述，加上ESS日均摊成本作为随机模型的目标函数，如式(2)所示：

(2)

式中：E代表数学期望值计算；ICp和ICSOC为单位功率和单位容量费用系数；FCcost包括所有N台机组在T时间段内总的机组燃料费用和启停费用，见式(3)所示：

SDi·xi(t-1)·(1-xit)]

(3)

式中：F(Pit)=ai·(Pit)2+bi·Pit+ci，ai，bi和ci是燃料费用系数，Pit是机组i在时刻t的有功功率。式(2)中第二、三项代表储能安装和运行费用，通常与ESS的额定功率和额定容量有关，而单位功率和单位容量费用系数可依据资本收益率按天均摊计算获得[6]。

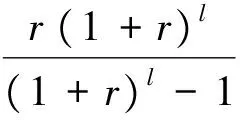
(4)

(5)

式中：Invp和Invc代表每单位容量和单位功率一次性安装费用，S|/MW和S|/MW·h；OMc为ESS年运行和维护费用，S|/(MW·h*Year)；l为ESS的寿命，Year；r为投资回报率；Ndays是一年的天数。

ESS随机规划模型的常规机组功率平衡等约束和ESS自有特性约束如下：

(1)系统的有功功率平衡约束：

(6)

(2)系统上、下旋转备用约束如公式(7)～(8)所示：

(3)机组爬坡率约束如式(9)～(10)所示：

(4)机组功率上下限约束

Pi,min·xit≤Pit≤Pi,max·xit

(11)

(5)机组最小开停机时间约束

(12)

(13)

(6)ESS的充放电功率约束

(14)

(15)

(7)ESS的充放电状态约束

uch,t+udis,t≤1

(16)

(8)ESS的SOC储能约束

SOCt=SOC(t-1)+Pch,t·Δt-Pdis,t·Δt

(17)

(18)

(9)ESS能量连续使用约束，即ESS起始储能等于调度结束时的储能

SOCT=SOC0

(19)

上述模型考虑了风电功率的随机性，如何处理与不确定变量相关的约束(6)和目标函数(1)的期望值是求解模型的关键。下文将提出基于点估计法和分支定界法的混合计算方案来求解该模型。

2 ESS随机规划模型的求解

2.1点估计法

点估计法是求解随机问题的有效方法，常见的有2m，2m+1和4m+1点估计法[15]。基于2m+1点估计法通过较低运算量就可获得较高精度的计算结果，本文将采用2m+1点估计法来处理所提的ESS随机规划模型。

在模型中，设定每小时风电为一个随机变量，T小时的风电便形成了T维的随机向量，记为(pw1,pw2,…,pwt,…,pwT)。据2m+1点估计理论[16]，随机向量样本通过以下方式产生：对t(t=1,2,…,T)时刻的风电功率用三个典型值pwt,k(k=1, 2, 3)代替，而剩下T-1个随机变量固定在其均值μw1,μw2,…,μwT，因此处理第t时刻的随机变量pwt，便会产生3组风电样本值 (μw1,μw2,…pwt,k,…,μwT) (k=1,2,3)。对于T小时的风电随机向量，最终会产生3T组风电样本值(μw1,μw2,…pwt,k,…,μwT) (k=1,2,3；t=1,2,…,T)。典型值pwt,k(k=1, 2, 3)计算如下：

pwt,k=μwt+εt,k·σwtk=1,2,3;t=1,2,…T

(20)

式中：εt,k是标准化的位置系数；μwt和σwt为第t小时风电出力pwt的均值和方差，可从1.1节风电功率的概率曲线获得。而位置系数εt,k和权重ωt,k可按式(21)～(22)计算[16]：

(21)

(22)

式中：λt,3和λt,4是第t小时风电功率pwt的偏度和峰度。另外式(22)中，εt,3=0导致pwt,k=μwt, 因此T组风电样本均相同为：(μw1,μw2,…,μwt,…,μwT)，而它们对应的权重系数之和为

(23)

进而3T组风电样本减少为2T+1组风电样本。对于2T+1组数据，通过求解常规UC问题可获得2T+1次系统燃料费用值。记2T+1次燃料费用为FCs，对应权重系数为ζs(s=1,2,…, 2T+1)，则2T+1组样本对应的燃料费用期望值为

(24)

将式(24)代入式(2)，所提模型的目标函数转化为式(25)：

(25)

采用类似手法，将式(6)中风电Pwt用点估计法产生的风电样本代替，并计及Pwt对其他变量的影响，ESS随机规划模型的约束(6)～(19)即转化为附录中式(A1)～(A14)。最终通过点估计法将ESS的随机规划模型(1)～(19)转化为确定性优化模型，其包含目标函数(25)和约束(A1)～(A14)。(记为模型B)。

2.2基于点估计及分支定界的混合计算方案

(1)首先，根据点估计法产生2T+1组风电样本(pw1,pw2,…,pwt,…,pwT)及对应权重系数ζs(s=1, 2,…, 2T+1)；

(4)根据FCs(s=1, 2,…, 2T+1)及对应的权重ζs计算系统燃料费用期望值，再依据式(25)加上ESS的安装和运行日均摊费用，获得系统总费用；

3 算例仿真

当10机系统配置锌溴储能时，系统总费用为4 495 641.6S|如表1所示，储能配置额定功率和安装容量均为零。上述表明，当10机系统尝试安装锌溴储能时，由于安装与运行费用较高，超过了锌溴储能带来的收益，因此不适合安装。考虑配置钠硫储能和超导磁储能，系统总费用分别为4 495 293.6S|/天和S|4 495 506.1S|/天，和未配置储能装置相比，系统总费用分别减少S|348/天和S|135.5/天。对4种不同形式的储能进行比较，铅酸储能具有较便宜的单位功率和单位容量费用系数为59.39S|/MW和40.02 S|/MW·h，因此其对应最为经济的系统总费用，可配置功率和容量也较高。可见，储能系统的单位成本费用是影响ESS容量配置的关键因素之一，当ESS的单价较低时，可配置较大规模的ESS以减少系统总费用。

另外，在本文ESS规划结果基础上，可进一步建立ESS充放电过程的动态模型，并以风电的功率波动量为信号参考，通过分布式控制[21-22]或者下垂控制[23]等实现风电功率波动的有效平抑。

表1 10机系统安装ESS前后的费用对比

表2 两种方法的ESS优化结果对比

4 结 论

本文对不确定风电环境下的风储有效配合问题，提出了ESS功率和容量最优配置的随机规划模型。该随机模型包含了长期风电的概率特征，考虑了常规机组和ESS的运行约束，且目标函数兼顾了机组费用期望值以及ESS的安装和运行日均摊费用。与文献[13]按天滚动求解UC相比，所提模型将风电的概率特征直接考虑到ESS配置问题中，所提模型扩展性好，对含大量风电数据的储能长期规划问题具有很好的适应性和扩展性。为求解该模型，文中提出了基于点估计和并行BB的综合求解方案，可快速有效地计算ESS的最优功率和容量配置。

[1] CHAKRABORTY S, SENJYU T, TOYAMA H, et al. Determination methodology for optimising the energy storage size for power system[J]. IET Generation, Transmission & Distribution, 2009, 3(11): 987-999.

[2] 练海晴，田亮，张锐锋. 空冷机组凝结水系统蓄能容量定量分析[J]. 华北电力大学学报(自然科学版), 2016, 43(1): 71-75.

[3] 文艺，张步涵，毛承雄，等. 风电场中储能系统的功率和容量优化配置[J]. 湖北工业大学学报, 2012, 27(1): 18-21.

[4] 张峰，董晓明，梁军，等. 考虑目标分解及其互补平抑的风电场复合储能容量优化[J]. 电力系统自动化， 2014, 38(7): 9-15.

[5] DEFOREST N, MENDES G, STADLER M, et al. Optimal deployment of thermal energy storage under diverse economic and climate conditions[J]. Applied Energy, 2014, 119: 488-496.

[6] CHEN S X, GOOI H B, WANG M Q. Sizing of energy storage for microgrids[J]. IEEE Transactions on Smart Grid, 2012, 3(1): 142-151.

[7] MOHAMMADI S, MOHAMMADI A. Stochastic scenario-based model and investigating size of battery energy storage and thermal energy storage for micro-grid[J]. International Journal of Electrical Power and Energy Systems, 2014, 61: 531-546.

[8] 吴晨曦，文福拴，李梅. 计及储能系统充放电策略的风光混合发电系统容量优化[J]. 华北电力大学学报(自然科学版), 2014, 41(4): 22-29.

[9] 王成山，于波，肖峻，等. 平滑可再生能源发电系统输出波动的储能系统容量优化方法[J]. 中国电机工程学报, 2012, 32(16): 1-8.

[10] 何勇琪，张建成，鲍雪娜. 并网型风光储混合发电系统中储能系统容量优化研究[J]. 华北电力大学学报(自然科学版), 2012, 39(4): 1-5.

[11] 叶瑞丽，郭志忠，刘瑞叶，等. 基于风电功率预测误差分析的风电场储能容量优化方法[J]. 电力系统自动化, 2014, 38(16): 28-34.

[12] KERDPHOL T, FUJI K, MITANI Y, et al. Optimization of a battery energy storage system using particle swarm optimization for stand-alone microgrids[J]. International Journal of Electrical Power and Energy Systems, 2016, 81: 32-39.

[13] PANDZIC H, WANG Y, QIU T, et al. Near-optimal method for siting and sizing of distributed storage in a transmission network[J]. IEEE Transactions on Power System, 2015, 30(5): 2288-2300.

[14] Elia. Wind-Power Generation Data[OL]. 2014. http://www.elia.be/ en/grid-data/power-generation/wind-power.

[15] MORALES J M, PEREZ-RUIZ J. Point estimate schemes to solve the probabilistic power flow[J]. IEEE Transactions on Power System, 2007, 22(4): 1594-1601.

[16] HONG H P. An efficient point estimate method for probabilistic analysis[J]. Reliability Engineering and System Safety, 1998, 59(3): 261-267.

[17] WOLSEY L A. Integer Programming[M]. New York: John Wiley & Sons, 1998.

[18] KAZARLIS S A, BAKIRTZIS A G, PETRIDIS V. A genetic algorithm solution to the unit commitment problem[J]. IEEE Transactions on Power System, 1996, 11(1): 83-92.

[19] SCHOENUNG S M, EYER J. Benefit/cost framework for evaluating modular energy storage[J]. SANDIA REPORT, 2008.

[20] IBM. High-performance mathematical programming solver for linear programming, mixed integer programming, and quadratic programming[OL]. 2014. http://www-01.ibm.com/software/commerce/ optimization/cplex-optimizer/.

[21] XU Y, ZHANG W, HUG G, et al. Cooperative control of distributed energy storage systems in a microgrid[J]. IEEE Transactions on Smart Grid, 2015, 6(1): 238-248.

[22] LUO X, XIA S, CHAN K W. A decentralized charging control strategy for plug-in electric vehicles to mitigate wind farm intermittency and enhance frequency regulation[J]. Journal of Power Sources, 2014, 248: 604-614.

[23] 麻常辉，潘志远，刘超男，等. 基于自适应下垂控制的风光储微网调频研究[J]. 电力系统保护与控制, 2015,43(23): 21-27.

Optimal Rated Power and Capacity of Energy Storage Sources for Wind Power Grids Based on Unit Commitment

LIU Yongmin1, XIA Shiwei2, YU Linlin1, LI Gengyin2, HUANG Jinghui1

(1. Economic Research Institute of State Grid Henan Electric Power Company, Zhengzhou 450052,China;2．State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources, North China Electric Power University, Beijing 102206,China)

Configuring appropriate Energy Storage Sources (ESSs) for wind power grid could effectively mitigate its power fluctuations and improve the system operation efficiency. This paper firstly analyzes the stochastic characteristics of power fluctuations of wind power grid, and then based on unit commitment (UC), proposes the ESS stochastic programming model which takes into account the amortized daily average of ESS installation and operation costs plus the expected fuel costs of conventional units. In order to effectively solve the model, a hybrid computation approach based on the Point Estimation (PE) strategy and the Parallel Branch and Bound (PBB) algorithm is designed to efficiently calculate the optimal rated power and energy capacity of ESS. Finally, the performance of four different typical ESSs is investigated in details by the 10-generator power grid penetrated with wind generations. The simulation results show that the proposed ESS stochastic planning model is effective and the corresponding solution approach is efficient for solving the model.

wind power grid; stochastic characteristics; unit commitment; energy storage sources; point estimation; parallel branch and bound algorithm

10.3969/j.ISSN.1007-2691.2017.05.03

TM76

A

1007-2691(2017)05-0018-09

2016-12-16.

北京市自然科学基金资助项目(3174057)；中央高校基本科研业务费专项资金资助项目(2016MS14).

刘永民(1976-)，男，高级工程师，研究方向为电力系统规划与设计；夏世威(1984-)，男，讲师，研究方向为新能源电力系统优化运行；于琳琳(1984-)，女，工程师，研究方向为电力系统规划与设计；李庚银(1960-)，教授，博士生导师，研究方向为电力系统分析、运行与控制；黄景慧(1977-)，女，高级工程师，研究方向为电力系统规划与设计。

附录

对ESS的随机规划模型采用点估计法后，原约束(6)～(19)转化为如下约束(A1)～(A14)

式中：变量带上标s代表在第s个风电功率样本值下的对应变量。

表A-1 10机系统的负荷功率值及威布尔分布风电功率

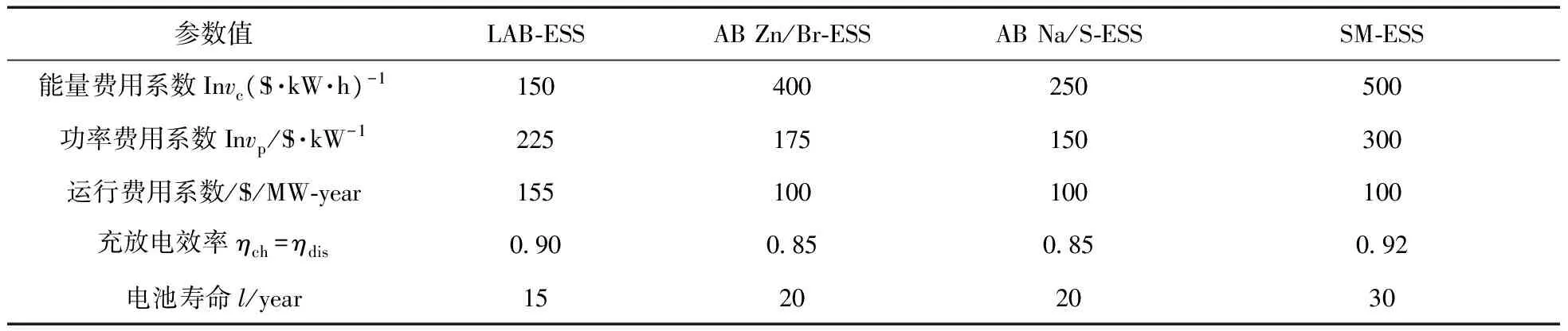
表A-2 4种典型ESS的参数

表A-3 10机系统的常规机组费用系数