基于零速/航向自观测/地磁匹配的行人导航算法研究
黄欣, 熊智, 许建新, 徐丽敏
(南京航空航天大学 自动化学院, 江苏 南京 210016)
基于零速/航向自观测/地磁匹配的行人导航算法研究
黄欣, 熊智, 许建新, 徐丽敏
(南京航空航天大学 自动化学院, 江苏 南京 210016)
目前行人导航技术正发挥着越来越重要的作用,而无全球导航卫星系统(GNSS)环境下的行人导航定位成为其不可或缺的环节。以自包含传感器为硬件平台,针对无GNSS环境下的行人自主导航定位展开研究,提出一种基于“2+2”分级模式的零速判别方法,并设计一种惯性导航系统的零速修正卡尔曼滤波算法,有效提高同一参数阈值下零速判别的准确性与可靠性、抑制传感器误差发散;研究行人初始静态下磁航向误差观测算法及行人运动状态下的零速航向误差自观测算法,解决了行人长时间行走航向发散问题;提出基于多层约束和K近邻算法的地磁匹配算法,并实现基于零速修正/航向误差自观测的行人导航算法与地磁匹配算法的融合,提高了行人导航定位精度与可靠性。实际数据测试验证,所提基于零速修正/航向误差自观测/地磁匹配的行人导航算法可有效提高定位精度79%以上。
控制科学与技术; 组合导航; 零速分级判别; 卡尔曼滤波; 航向误差自观测; 地磁匹配; 多层约束
0 引言
目前,国内外已经掀起研究行人导航技术的热潮。无论商场购物、生活健身、野外勘探还是火灾救援,行人导航定位正发挥着越来越重要的作用。室外环境下,行人可以借助全球导航卫星系统(GNSS)实现定位,但是在室内环境下,卫星信号微弱甚至缺失,因此有必要针对无GNSS环境下的行人导航定位展开更深入的研究。
目前,许多学者专家均已针对无GNSS环境下的行人导航定位开展了大量的研究工作,研究内容主要包括以下两方面:1)借助无线网络辅助行人定位,如蓝牙、无线保真(WIFI)、超宽带(UWB)等其他射频辅助信息;2)基于固定于行人头部、肩部、腰部和脚部的惯性传感器,通过观测惯性传感器的运动特性,借助零速修正技术(ZUPT)和零角速修正(ZARU)技术,辅助惯性导航系统实现高精度行人定位。其中,根据腰部和胫骨的传感器特性,文献[1]使用支持向量机(SVM)分析行人步态并借助ZUPT实现了行人定位,但未针对不同行人/不同步速下ZUPT的可靠性开展研究,同时该方法的航向可观测性较差、航向误差难以消除;文献[2]提出了一种利用双惯性测量单元(IMU)架构实现室内行人定位的方法,但该方法会增加额外成本,不适合广泛推广;文献[3]采用额外射频信息来辅助修正惯性导航(简称惯导)位置误差,但该方法的应用场景较狭窄、可移植性较差;文献[4]融合建筑物楼向信息来提高行人导航航向的精度,但该方法的适用范围受到限制、灵活性较低。
地磁场作为地球的固有属性,已广泛用于航向计算。限于室内金属会产生硬磁和软磁干扰,即磁异常现象,室内磁航向的精度难以保证。虽然许多学者已经提出了地磁标定方法,包括二维椭圆标定和三维椭球标定技术等,但仍然难以消除室内全程磁误差。部分学者研究利用磁异常来构建地磁指纹库,利用地磁匹配(GM)技术实现行人定位,但是提出的部分方案消耗内存较大且实时性较差,不适合工程实际应用,如动态时间规整(DTW)算法、Hausdorff距离算法等[5-8]。
本文针对上述问题,构建了基于捷联惯性导航技术与GM技术的行人组合导航算法模型,主要解决无GNSS环境下的高精度、高可靠性行人导航定位问题。该方法研究了基于“2+2”分级模式的零速综合判别方法,并设计了一种基于惯导系统的零速修正卡尔曼滤波算法,以有效提高同一阈值下零速判别的准确性与可靠性,解决不同行人、不同步速的适应性问题,抑制传感器误差发散;研究了行人初始静态下基于磁航向稳定性的航向误差观测算法(MHESO)及行人运动状态下的零速航向误差自观测算法(ZHESO),增强了行人航向可观测性,提高了航向精度;研究了基于多层约束和K近邻(KNN)算法的GM模型,并实现了基于零速修正/航向误差自观测(ZUPT_HESO)的捷联惯性导航算法与GM的融合,进一步提高了行人导航定位精度。本文所提出的基于零速修正/航向误差自观测/地磁匹配(ZUPT_HESO_GM)的行人导航算法在保证高精度的基础上,大大保证了无GNSS环境下行人导航定位的可靠性。
1 行人运动特性和地磁特性分析
1.1 行人运动特性
正常步态周期下,行人脚后跟首先着地,表现为加速度计产生一个很大的峰值。伴随着行人脚部的阻尼振动,陀螺仪反映出连续的峰值输出。当行人单脚着地时,加速度计与陀螺仪进入稳态,即零速状态,此时可以借助ZUPT或ZARU抑制误差发散。如图1所示(为与后续零速检测算法相对应,均取3轴幅值的平方),行人正常步态下,零速状态与摆动状态交替出现。稳态下,行人速度的理论值为0,位置基本保持不变。

图1 加速度计与陀螺仪零速/摆动交替示意图Fig.1 ZUPT/swing alternation of accelerometer and gyroscope
1.2 地磁特性

图2 地磁组成Fig.2 Components of geomagnetism
地球磁场具有7大属性,如图2所示,包括水平磁场强度H、垂直磁场强度Z、总磁场强度F、北向磁场强度X、东向磁场强度Y、倾角I和磁航向角D[9]. 凭借这7大属性,可以构建指纹库、实现GM. 构建指纹库之前需满足先决条件,即不同位置之间的磁场强度需有明显的变化,变化越大,匹配误差越小;相同位置的磁指纹需保持长期不变[10]。


图3 小范围总磁场强度变化示意Fig.3 Change of total magnetic field strength in a small range

图4 不同时间段总磁场强度对比Fig.4 Comparison of total magnetic field strengths in different time periods
2 行人导航算法构建与融合
2.1 基于ZUPT_HESO的行人导航算法
行人运动特性和地磁特性是构建行人导航定位误差修正模型的基础,而行人导航解算算法是实现行人导航定位的前提。本文研究了基于足部的捷联惯性导航解算算法,包括姿态解算、速度解算和位置解算,如(1)式[11]所示:
(1)

(2)
式中:ab和ωb分别为3轴加速度计零偏和3轴陀螺仪零偏;N为用于求取零偏的个数;ai和ωi分别为第i个3轴加速度与3轴角速度数据信息。
由于IMU零位偏差会随时间漂移,在缺乏其他系统辅助的情况下,纯捷联解算精度无法满足行人的日常需求。因此,本文研究利用行人运动学特性来抑制位置、速度误差的漂移。
在行人的行走过程中,加速度计与陀螺仪周期性变化。考虑到传感器单轴误差及3轴间的耦合影响,构建如下4种子零速判别方式:
(3)
(4)
(5)
(6)
式中:akx、aky、akz代表第k时刻加速度计采集得到的3轴加速度信息;ωkx、ωky、ωkz代表第k时刻陀螺仪采集得到的3轴角速度信息;n为方差计算区间大小;εa、εω、εa2和εω2分别为人为设定的阈值。
考虑到不同行人、不同步速及固定参数阈值下,仅用λ1、λ2、λ3、λ4其中之一进行零速判别稳定性较差,容易发生误判或者漏判,同时鉴于不同行人、不同步速下3轴加速度计模值方差与3轴陀螺仪模值方差的稳定性较强(即模值方差的大小基本不变),针对4种子零速研究采用“2+2”分级模式判别总零速的起始时刻和终结时刻。即用加速度计与陀螺仪的方差子零速(λ1和λ2)判别出总零速的起始时刻;以加速度计与陀螺仪的幅值子零速(λ3和λ4)判别出总零速的终结时刻,以此提高不同行人、不同步速下,同一参数阈值的可靠性。图5所示为一步零速区间判别示意图。由图5可见,第1级判别(蓝色)为方差子零速判别曲线,第2级判别(棕色)为幅值子零速判别曲线,红色为综合零速判别曲线。由于方差子零速计算区间为20,第20个时刻与前19个时刻的耦合性较强,当第20个时刻为行人运动态时,前19个时刻亦判为非零速态,将出现漏判现象,此时需用幅值子零速进行进一步判别。同时,每一级利用加速度计与陀螺仪两者共同作用,可以抑制零速误判现象。

图5 “2+2”零速分级判别示意图Fig.5 Schematic diagram of ZUPT detection based on “2+2”hierarchical model
对于第2级模式,λ3和λ4作适当调整,形如λ5和λ6,如(7)式所示。其中:当k-1时刻λ1(k-1)=1且k时刻λ1(k)=0时a_number=1,当λ5(k)=0时a_number=0,当a_number>0且λ5(k)=1时a_number=a_number+1;同理,当k-1时刻λ2(k-1)=1且k时刻λ2(k)=0时ω_number=1,当λ6(k)=0时ω_number=0,当ω_number>0且λ6(k)=1时ω_number=ω_number+1. 其中,a_number和ω_number分别为加速度计与陀螺仪幅值的子零速个数。
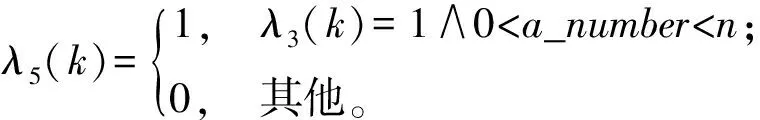
(7)
子零速综合判别模型如(8)式所示:

(8)
式中:Z(k)表示k时刻的综合零速判别结果,若为1则表示当前时刻行人为理论上的零速时刻。流程示意如图6所示。本文针对λ1(k)、λ2(k)、λ3(k)、λ4(k)判别方式和本文提出的Z(k)判别算法进行了不同步速、不同行人穿戴下的大量测试,其中一组零速判别效果如图7所示,可以发现λ1(k)、λ2(k)、λ3(k)、λ4(k)判别方式存在误判现象。由此可见本文方法能有效保证在同一阈值下不同行人、不同步速下零速判别的准确性和可靠性,提高了参数的可重载能力。
图7(a)和图7(b)中绿色曲线为综合零速检测曲线(高电平为检测到零速,幅值仅为显示用),红色曲线分别为单加速度计、单陀螺仪零速检测曲线。
部分学者在零速状态下将速度置0,无法有效估计速度、位置、姿态及传感器误差。本文提出利用卡尔曼滤波器、基于人体运动学设计来构建综合零速观测模型,在检测到零速时,利用卡尔曼滤波器估计速度、位置、姿态及传感器误差,抑制误差发散。
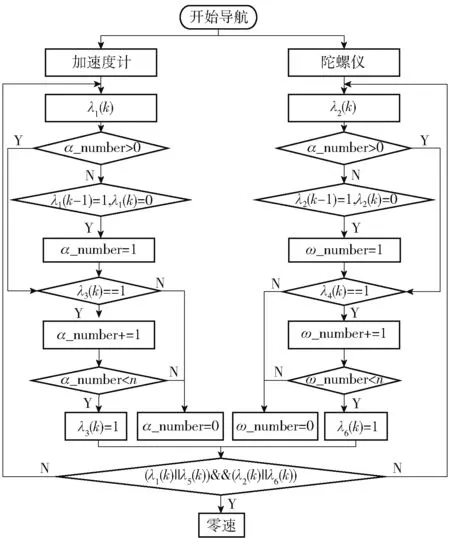
图6 零速综合判别示意图Fig.6 Flow chart of ZUPT comprehensive judgment

图7 零速检测对比曲线Fig.7 Comparison of ZUPT detection
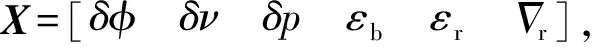

(9)
式中:A为系统矩阵;G为系统噪声矩阵;W为系统噪声。
利用伪量测信息构建零速状态下的六维量测模型。令veloPk=[0;0;0],posiPk=posiNk-1(k-1表示上一时刻),则零速状态下的量测方程如(10)式所示(增加位置量测量相比于仅有速度量测可以提升7%的定位精度):
(10)
式中:Zvp(t)为观测量;veloN和posiN为惯导实时解算的速度、位置;Mv和Mp为行人零速状态下速度误差与位置误差;Hvp为量测矩阵,如(11)式和(12)式所示;Vvp为量测噪声。
(11)
(12)
式中:L为纬度;Rm和Rn分别为子午圈和卯酉圈半径。
同时,限于零速周期非一致性,本文对比了固定离散周期和时变离散周期的差异,并最终选择(13)式所示的方案,即时变离散周期。
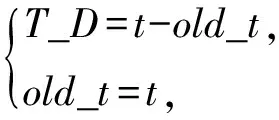
(13)
式中:old_t为上一个零速时刻;t为当前零速时刻。
因此得到最基本的基于ZUPT的行人导航算法如图8所示,包括惯性测量单元、零速检测单元、卡尔曼滤波单元及导航计算单元。

图8 基于ZUPT的行人导航算法框架Fig.8 Framework of ZUPT-based pedestrian navigation algorithm
在上述基础上研究了行人初始静止状态下MHESO模型及行人运动状态下ZHESO模型,以增强航向可观测性。
行人初始静止状态下,磁航向角(利用二维椭圆标定)具有较强的稳定性,因此构建一维量测方程,如(14)式所示:
Zmφ(t)=[ψINS-ψmg]=[δφ+Mmφ]=
Hmφ(t)X(t)+Vmφ(t),
(14)
式中:ψINS为捷联解算的航向角;ψmg为磁航向角;Mmφ为磁航向角解算误差;Hmφ为量测矩阵;Vmφ为量测噪声。
行人初始静止状态下,利用(15)式实现对传感器误差进一步估计:
(15)
行人运动状态下,每一步经历一段零速时刻,记该步第1零速时刻点的航向角为ψk-i,如图9所示,其中红点表示每一步的第1零速时刻点。
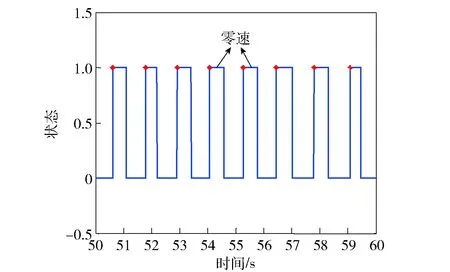
图9 零速航向自观测示意Fig.9 Indication of heading error self-observation
记该步其余零速时刻点的航向角为ψk-o,理论上零速段的计算公式为
Δψ=ψk-i-ψk-o=0.
(16)
构建零速航向自观测量测方程为
Zzφ(t)=[ψk-i-ψk-o]=[δφ+Mzφ]=
Hzφ(t)X(t)+Vzφ(t).
(17)
由于姿态误差角与平台误差角存在如下关系:
(18)
式中:θ为俯仰角;δφx、δφy和δφy为3个平台误差角。因此:

(19)
于是可得运动状态下ZUPT_HESO算法的7维量测模型为
(20)
即在每一步中,在零速阶段利用零速航向误差自观测算法估计航向误差与陀螺误差。
2.2GM算法
本文将GM分为两种场景:1)人- 人跟踪模式;2)非跟踪模式。部分专家学者已经针对室内地磁异常特性提出了相应的匹配算法[13-15],包括动态时间规整算法、Hausdorff距离算法与最小距离算法。各种算法的对比如表1所示。

表1 GM算法对比
表1中:H为总距离之和;d为两点间距离;A和B分别为磁指纹库及欲匹配磁数据;i和j分别为A和B的当前时刻;r=1,2,分别代表曼哈顿距离和欧氏距离。由表1可见,同一路径下,行人的行走速度不同将导致磁数据间隔的收缩或放大,如图10所示(黑色代表两磁场数据最为接近),此时相关度匹配误差较大。动态时间规整算法虽然可以避免同一路径不同行走速度下的动态影响,但是内存消耗较大且无法实现实时;Hausdorff距离算法需要事先获取所有欲匹配磁信息,不适合工程实际应用;第3种算法需要设置约束条件以避免误匹配[13]。

图10 同一路径不同速度下的磁对应示意图Fig.10 Magnetic map of the same path at different speeds
本文在上述算法的基础上,研究利用KNN算法和多层约束实现GM. KNN算法属于机器学习方法,依赖于极限理论,但只有少量的相邻样本与决策类型相关。本文实际运用中利用了准时制(JIT)理论来加速循环。为更加精准地实现GM,本文设置了多层约束,并基于两种场景构建两种不同的多层约束模型,其中人- 人跟踪场景下的多层约束模型如(21)式所示:
(21)
式中:i和j分别表示实时采集的磁与指纹库序列号;ε1表示前后间隔;ε2为GM误差;ti和tj分别为指纹库时间点和实时采集地磁时间点。多层约束限制了其分类范围并有助于选择匹配点。每当GM成功,更新last_MM=tj.
另一场景为非跟踪状态,此时需适当修改多层约束,如(22)式所示:
(22)
式中:posiMj为指纹库的位置;posiNi为当前点的位置,由基于ZUPT_HESO的行人导航算法得到。每当GM成功,更新last_MM=tj. 利用实时采集的磁信息,借助KNN算法和多层约束进行磁匹配,若满足多层约束则磁匹配成功。
2.3ZUPT_HESO_GM算法
事实上,虽然借助ZUPT、卡尔曼滤波估计技术及ZHESO算法能有效抑制惯导误差发散,但是无法保证百分之百的成功率;GM受限于室内环境,且不能提供连续的位置信息。因此,本文有效组合两种算法,在保证行人导航定位精度的前提下,提高其可靠性。
在正常环境下,由基于ZUPT_HESO的行人导航算法提供位置信息。当仅有GM成功时,采用(23)式修正惯导误差;当同时检测到零速及GM成功时,使用集中滤波器构建8维量测,辅助修正位置误差、速度误差及传感器误差,如(24)式所示。整个组合导航系统框架如图11所示。
Z6(t)=[posiN-posiM]=[δp+M6]=

(23)
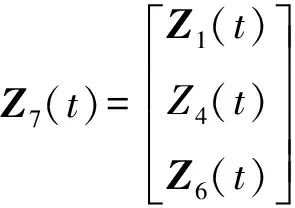
(24)

图11 组合导航系统框架Fig.11 Framework of integrated navigation system
3 行人导航实验
3.1 测试路径构建及地磁指纹库的构建
为了测试算法的可行性,分别于室外和室内选择测试路径,其中两条路径如图12和图13所示。图12为室外环绕足球场轮廓,耗时约10 min;图13为室内方形多圈行走,耗时约5 min. 测试前利用高精度激光测距仪测量得到相对距离。本文实验采用荷兰Xsens公司生产的MTi-30器件(见图14)采集室内磁信息。磁采集频率为100 Hz,加速度计与陀螺仪采集频率为200 Hz.
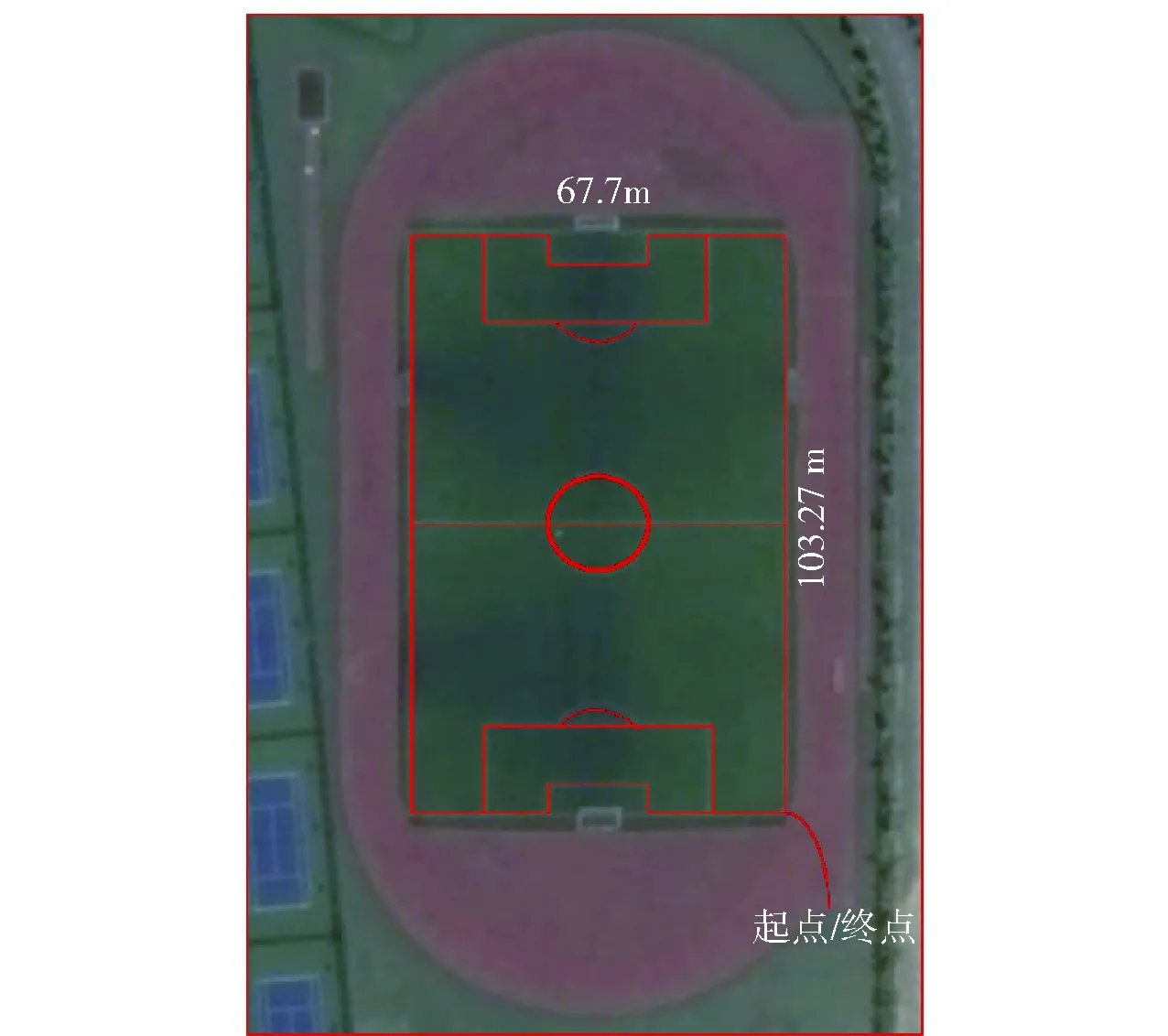
图12 室外路径Fig.12 Outdoor path
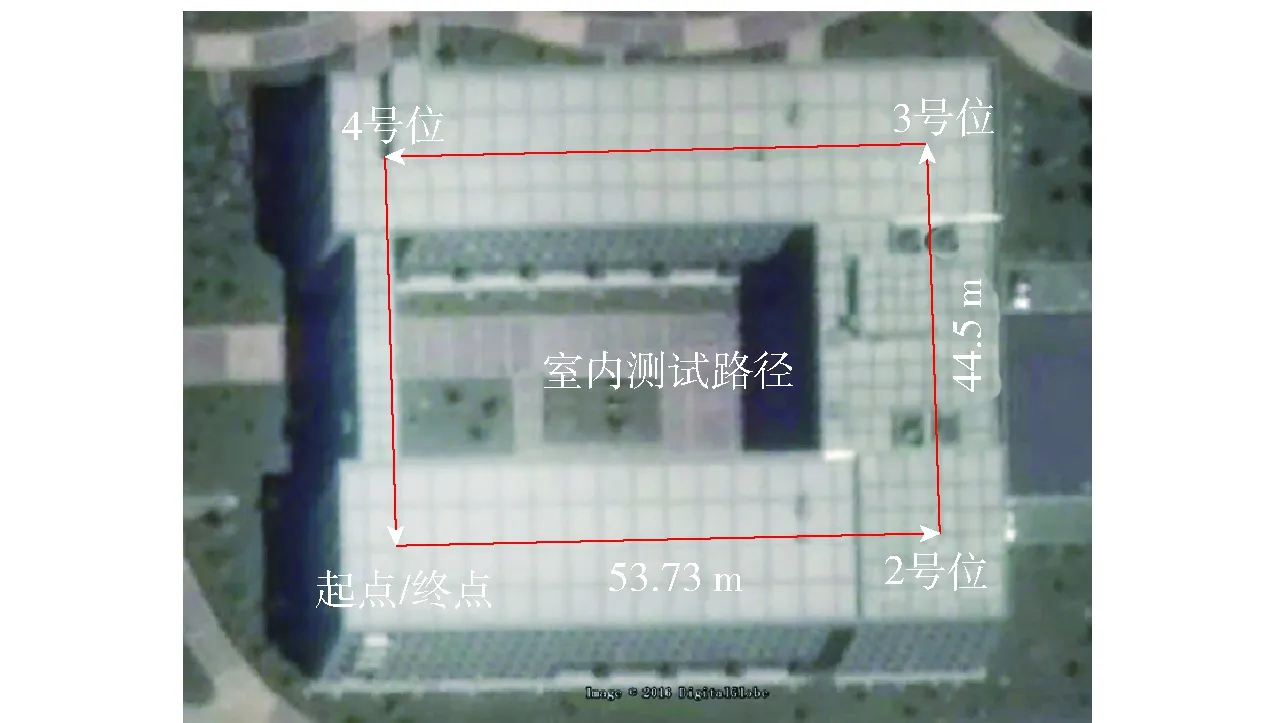
图13 室内路径Fig.13 Indoor path

图14 MTi-30外观图Fig.14 MTi-30
3.2 算法实验验证
下面验证上述算法的可行性,主要包括以下3部分:
1) ZUPT算法。基于低成本的纯捷联惯性导航解算算法误差发散较快,两种场景下误差可达千米级,导航曲线与真实路径完全不相匹配;在捷联惯性导航的基础上,增加了零速修正算法。如图15(a)与图15(b)中蓝色曲线为加入零速修正的导航结果,导航曲线与真实路径已基本相同,但长时间导航状态下的最终误差稍大。
2) ZUPT-HESO算法。观测图15(a)与图15(b)中蓝色曲线,尽管有零速修正算法估计速度误差、位置误差和传感器误差,但由于航向可观测性较差,长时间导航时航向亦会发散。如表2所示,通过增加航向自观测算法有效提高了航向精度,降低了整体定位误差,室内和室外导航定位精度分别提高98.6%和79.3%. 如图15(a)与图15(b)中红色曲线所示,航向精度的提升反映在最终位置的误差较小。
3) ZUPT_HESO_GM算法。室内环境中的磁异常环境较明显,室内测试路径2中构建了地磁指纹库,其中地磁指纹间隔为10 cm,组合导航结果如图15(b)中的绿色曲线所示。由表2可见,室内定位精度在ZUPT_HESO算法的基础上提高了导航定位精度98.3%,进一步增加了无GNSS环境下行人导航定位的可靠性 。

图15 室内外路径不同算法效果对比Fig.15 Comparison of navigation effects in indoor and outdoor paths

表2 不同算法误差对比
综上,基于ZUPT_HESO_GM算法辅助的行人导航定位算法精度较好、可靠性较高。
4 结论
本文以自包含传感器为硬件基础,提出了一种基于ZUPT_HESO的捷联惯性导航解算算法与GM算法融合的组合导航算法。该方法研究了基于“2+2”分级零速判别模型下的ZUPT模型,基于卡尔曼滤波算法有效修正行人长时定位下的传感器误差与导航结果误差;设计了MHESO模型与ZHESO模型解决了行人航向发散问题;研究了基于多层约束和KNN算法的GM算法,并实现了基于ZUPT_HESO辅助的捷联惯性导航解算算法与GM算法融合,进一步提高了GNSS失效环境下的行人导航定位精度与可靠性。
References)
[1] 汪少初. 基于PDR的定位与跟踪技术研究及系统设计[D].天津:天津大学, 2014.
WANG Shao-chu. Research on the technologies of personnel positioning and tracking and system design based on PDR [D]. Tianjing: Tianjin University, 2014. (in Chinese)
[2] 徐元, 陈熙源, 李庆华,等. 一种基于双IMU框架的室内个人导航方法(英文)[J]. 中国惯性技术学报, 2015, 23(6):714-717.
XU Yuan, CHEN Xi-yuan, LI Qing-hua, et al. Indoor pedestrian navigation based on double-IMU framework [J]. Journal of Chinese Inertial Technology, 2015, 23(6):714-717. (in Chinese)
[3] Ruiz A R J, Granja F S, Honorato J C P, et al. Pedestrian indoor navigation by aiding a foot-mounted IMU with RFID signal strength measurements[C]∥International Conference on Indoor Positioning and Indoor Navigation. Zurich, Switzerland: IEEE, 2010.
[4] Abdulrahim K, Hide C, Hill T M C. Aiding low cost inertial navigation with building heading for pedestrian navigation [J]. Journal of Navigation, 2011, 64(2):219-233.
[5] 熊明亮, 刁梦雯, 赵国梁. 基于地球磁场的室内定位系统的研究[J]. 无线互联科技, 2015(18):14-15.
XIONG Ming-liang, DIAO Meng-wen, ZHAO Guo-liang. Research on indoor positioning system based on the magnetic field of the earth [J]. Wireless Internet Technology, 2015(18):14-15. (in Chinese)
[6] Robertson P, Frassl M, Angermann M, et al. Simultaneous localization and mapping for pedestrians using distortions of the local magnetic field intensity in large indoor environments[C]∥International Conference on Indoor Positioning and Indoor Navigation. Montbeliard-Belfort, France: IEEE, 2013.
[7] Liu K, Motta G, Ma T, et al. Multi-floor indoor navigation with geomagnetic field positioning and ant colony optimization algorithm[C]∥Proceedings of Symposium on Service-Oriented System Engineering. Oxford, UK: IEEE, 2016:314-323.
[8] 宋镖, 程磊, 周明达,等. 基于惯导辅助地磁的手机室内定位系统设计[J]. 传感技术学报, 2015, 28(8):1249-1254.
SONG Biao, CHENG Lei, ZHOU Ming-da, et al. The design of cellphone indoor positioning system based magnetic assisted inertial navigation technology [J]. Chinese Journal of Sensors and Actuators, 2015, 28(8):1249-1254. (in Chinese)
[9] Li Y, Zhuang Y, Zhang P, et al. An improved inertial/WiFi/magnetic fusion structure for indoor navigation [J]. Information Fusion, 2016, 34:101-119.
[10] Frassl M, Angermann M, Lichtenstern M, et al. Magnetic maps of indoor environments for precise localization of legged and non-legged locomotion[C]∥Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems. Tokyo, Japan: IEEE, 2013:913-920.
[11] Li Y, Zhuang Y, Lan H, et al. Self-contained indoor pedestrian navigation using smartphone sensors and magnetic features[J]. IEEE Sensors Journal, 2016, 16(19):1-1.
[12] Li Y, Georgy J, Niu X, et al. An automatic multi-level gyro calibration architecture for consumer portable devices[C]∥Proceedings of International Conference on Indoor Positioning and Indoor Navigation. Busan, Korea: IEEE, 2014:656-660.
[13] Ghose A, Pal A, Dutta Choudhury A, et al. Indoor positioning system: US, 9557178[P]. 2017-01-31.
[14] 孔亚男, 鲁浩, 徐剑芸. 基于Hausdorff距离的地磁匹配导航算法[J]. 航空兵器, 2011(4):26-29.
KONG Ya-nan, LU Hao, XU Jian-yun. Study on geomagnetic matching algorithm based on Hausdorff distance [J]. Aeroweaponry, 2011(4):26-29. (in Chinese)
[15] 刘玉霞,周军,葛致磊. 基于隐马尔可夫模型的地磁匹配算法[J].中国惯性技术学报, 2011, 19(2):224-228.
LIU Yu-xia, ZHOU Jun, GE Zhi-lei. Geomagnetic matching algorithm based on hidden Markov model[J]. Journal of Chinese Inertial Technology, 2011, 19(2):224-228.(in Chinese)
ResearchonPedestrianNavigationAlgorithmBasedonZeroVelocityUpdate/HeadingErrorSelf-observation/GeomagneticMatching
HUANG Xin, XIONG Zhi, XU Jian-xin, XU Li-min
(College of Automation Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, Jiangsu, China)
Nowadays, pedestrian navigation technology is playing an increasingly important role in supermarket shopping, fire rescue and field exploration, and the pedestrian navigation and positioning without global navigation satellite system (GNSS) has become an indispensable link. The self-contained sensors are used as a hardware platform for research on pedestrian autonomous navigation in non-GNSS environment. A zero-speed comprehensive discriminant algorithm based on the “2+2” hierarchical model is studied to improve the accuracy and reliability of zero velocity update (ZUPT). Kalman filter algorithm based on ZUPT designed for inertial navigation system is used to effectively suppress the sensor error divergence. To solve the problem of pedestrian long-term heading divergence, the magnetic heading error self-observation algorithm (MHESO) for pedestrian initial static state and the ZUPT heading error self-observation algorithm (ZHESO) for pedestrian movement are studied. In addition, a geomagnetic matching (GM) algorithm based on multi-layer constraint and K-nearest neighbor algorithm is proposed, and the fusion of ZUPT_HESO-pedestrian navigation algorithm and geomagnetic matching algorithm is realized, which improves the accuracy and reliability of pedestrian navigation. The actual data test proves that the proposed pedestrian navigation algorithm based on ZUPT_HESO_GM effectively improves the positioning accuracy by more than 79%.
control science and technology; integrated navigation; zero velocity update grading discrimination; Kalman filter; heading error self-observation; geomagnetic matching; multilayer constraint
2017-03-01
国家自然科学基金项目(61673208、61533008、61533009、61374115、61304227);江苏省“333工程”科研立项项目(BRA2016405);人力资源和社会保障部留学人员择优资助项目(2016年);江苏省六大人才高峰项目(2013-JY-013);江苏高校优势学科建设工程项目(2014年);中央高校基本科研业务费专项项目(NZ2016104、NS2017016);江苏省普通高校研究生科研创新计划项目(KYLX15_0264);江苏省自然科学基金项目(BK20141453);航空科学基金项目(20165552043)
黄欣(1993—),男,硕士研究生。E-mail:huangxin@nuaa.edu.cn
熊智(1976—),男,研究员,博士生导师。E-mail:xiongzhi@nuaa.edu.cn
V249.32+8
A
1000-1093(2017)10-2031-10
10.3969/j.issn.1000-1093.2017.10.020

