低雷诺数下不同湍流模型和差分格式对典型流场数值模拟预测的影响研究

殷结峰 高春燕 高义人



低雷诺数下不同湍流模型和差分格式对典型流场数值模拟预测的影响研究

殷结峰1高春燕2高义人3

（1.西安热工研究院有限公司 西安 710054；2.国网山东省店里公司聊城供电公司 聊城 252000；3.陕西燃气集团新能源发展有限公司 西安 710016）

由于湍流理论和数值模拟方法本身的局限，采用CFD来预测低雷诺数的流场本身存在一定的难度，同时各种计算模型的设置对于最后的计算精度也有很大的影响。选用了标准-、RNG-、Realizable-三种常用的湍流模型以及一阶迎风格式、二阶迎风格式、QUICK格式三种常用的差分格式对一个简化的典型流场进行模拟预测，对比分析不同的模拟设置变化对于流场计算结果的影响。

低雷诺数；湍流模型；差分格式

0 引言

湍流流动是一种不规则的流动状态，研究湍流的目的是预测和控制自然界各种复杂湍流。随着计算机的迅速发展，数值仿真成为近年来预测复杂湍流和研究湍流物理的主要手段之一。在进行模拟计算的过程中，计算模型的设置对于流场的预测的精度有着重要影响。对此，国内也有较多学者对解决不同问题时（如建筑室外风环境[1-3]、管道内流体的流态[4-6]，建筑室内通风[7]等问题）的计算模型的设置的差异进行了比较分析。但是，由于低雷诺数下流场的测量有较大难度以及计算机的计算能力有限等问题，CFD（Computational Fluid Dynamic）方法对于低雷诺数下的流场模拟仍有一定的难度。而低雷诺数的流态在实际的科研及工程中又不可避免，对于此种问题，在工程应用中，计算模型及边界条件的设置更多是根据经验来选定，存在较大的差异。

本文设定了一种典型的物理模型如图1所示，它可以视为是房间通风以及突扩管道等的简化模型。笔者选用了三种常用的-系列湍流模型（标准、RNG、Realizable）以及一阶迎风、二阶迎风、QUICK三种差分格式来对流程进行模拟计算。分析湍流模型以及差分格式对于流场预测的差异。

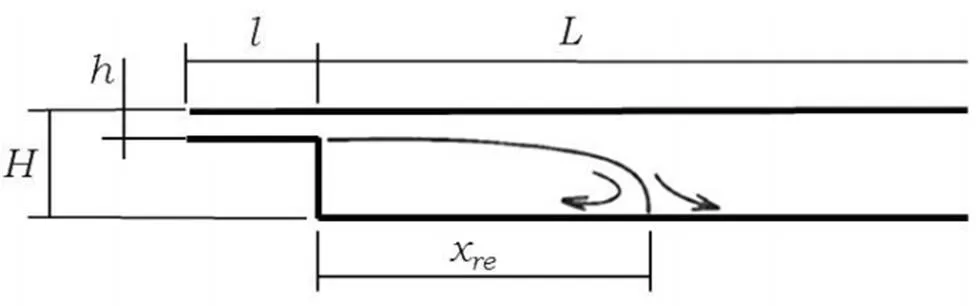
图1 模型计算区域二维图

1 物理模型及网格划分

如图1所示模型，取=100mm，=400mm，=4h，=40h作为流动的计算区域，其中X为回流区长度。由于选取的计算区域足够长，所以采用速度进口，压力出口边界条件。边壁为固体壁面无滑移，进口速度成抛物线分布，重力方向垂直于水平方向（大小取9.8m/s2）。文中选用空气和水两种流体介质其粘性系数分别为1.7894×e-5kg/(m·s)和1.001003kg/(m·s)，均设定为不可压缩理想气体。经过比较61800的网格数量具有较高的网格独立性以及计算效率。

2 湍流模型及差分方法

文中分别采用了三种湍流模型以及三种差分方式，分别介绍如下。

2.1 标准k-ε模型

在标准-模型中，湍动能和耗散率的控制方程为[8]：

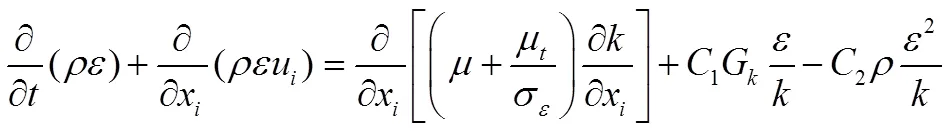
其中，湍流粘性系数μ=ρck2/，模型常数为C=0.99；1=1.44；2=1.92；σ=1.3；σ=1.3。

2.2 RNG k-ε模型

RNG-模型是基于重整化群的理论提出的（Renormalization Group），经改进，其控制方程与标准-模型形式相同，但是模型常数略有差异[9]。

c=0.085；2=1.68；σ=σ=0.7179。主要差别在于1不再是常数，而是表示为（湍流时间尺度与平均应变率之比）的函数，如公式（3）。

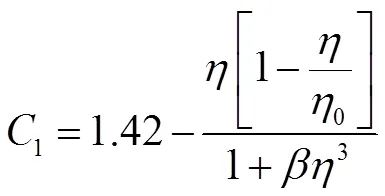
2.3 Realizable k-ε模型

Realizable-模型采用了新的耗散率方程[10]：

Realizable-模型常数为1=max[0.43,/+5]；2=1.9；σ=1.0；σ=1.2与标准-模型和RNG-模型的主要差别在于：C不再是常数，而是湍流时间尺度与应变张量和旋转张量的函数。

2.4 一阶迎风差分格式（First Order Upwind Sheme）

一阶迎风差分格式：即界面上的未知量恒取上游节点（即迎风侧的节点）的值。这种迎风格式具有一阶截差，因此叫一阶迎风格式。无论任何计算条件下都不会引起解的振荡，是绝对稳定的。但是当网格P数较大时，假扩散严重，为避免次问题通常需要加密网格。

2.5 二阶迎风差分格式（Second Order Upwind Sheme）

二阶迎风差分格式与一阶迎风格式的相同点在于，二者都通过上游单元节点的物理量来确定控制体积界面的物理量。但二阶格式不仅要用到上游最近一个节点的值，还要用到再上游的一个节点值。

2.6 QUICK差分格式

QUICK格式是对流项的二次迎风差值，是一种改进离散方程截差的方法，通过提高界面上插值函数的阶数来提高格式截断误差。对流项的QUICK格式具有三阶精度的截差，但是扩散项仍采用二阶截差的中心差分格式。

3 计算结果及分析

3.1 流场特性

图2～图3分别采用标准-、RNG-、Realizable-模型下，不同进口雷诺数时的罐内流线图，他们的差分格式都为二阶迎风差分格式。其中图2中的介质为空气，图3为水。流体从细管流入到突扩管中时，由于流体的惯性和突然扩大的边界条件，在管壁拐角与主流束之间形成分离和回流区，会引起压力降低和能量损失[11,12]。

从图2与图3的流线图中可以清晰的看到流体在管道中形成了上述的主流区与回流区，当入口Re=100时，无论流体介质时水还是空气都会在管道上方与下方形成两个回流区，随着入口Re数的增加上方回流区逐渐消失，但是下方回流长度区随着Re数的增大而增大。当流体介质不同时，回流区长度随入口Re数增加的变化也不同，在Re数为100、500时差异并不明显，当Re=1000时空气的回流区长度在2m左右，而水的回流区长度为1.7m，出现了显著的差异。通过观察流体中的回流核心位置，可以发现在Re分别在100、500和1000时，回流核心位置先后退再向前移。

图2 介质为空气时不同流速及湍流模型下管内流线图

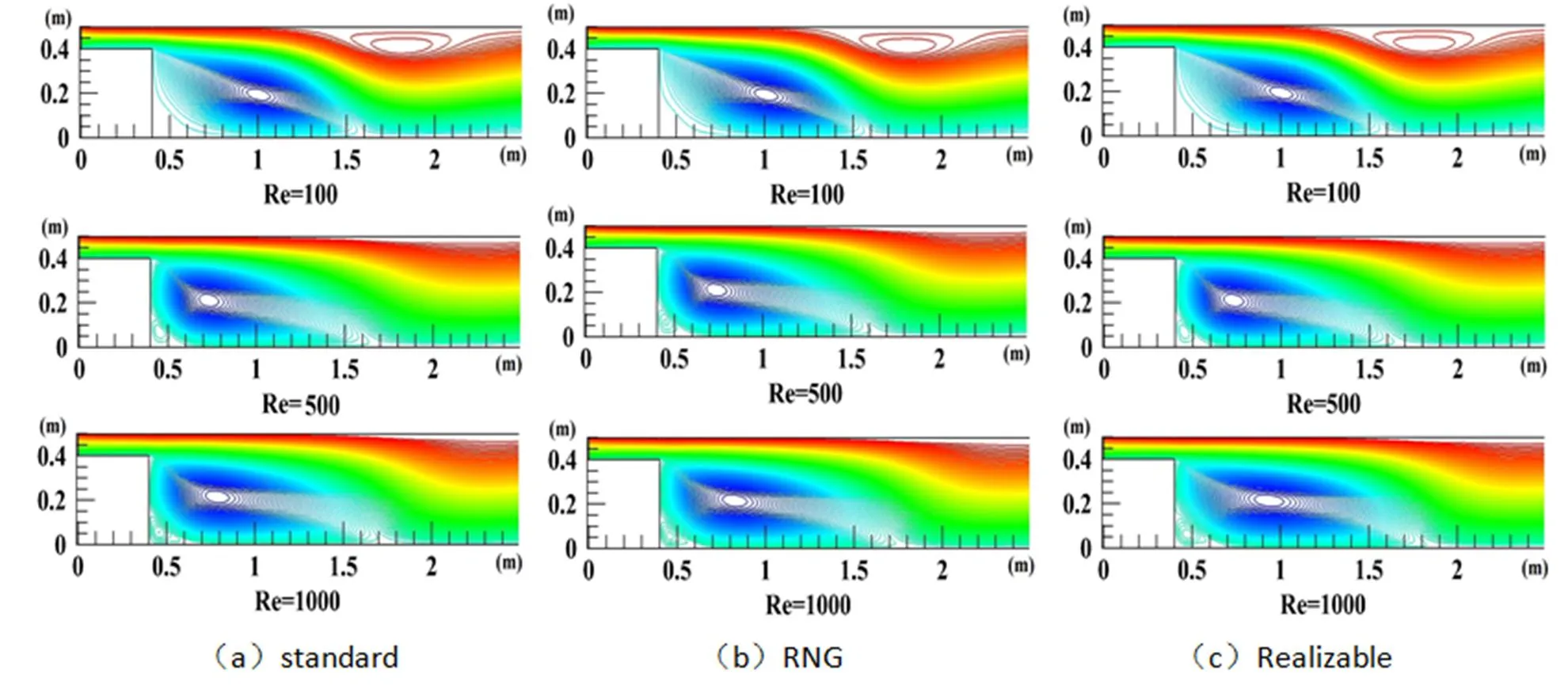
图3 介质为水时不同流速及湍流模型下管内流线图

3.2 对回流区的发展影响

观察不同湍流模型下回流区的发展状态，可以发现他们的流态大致相同，但是仔细观察仍有细微的差别，这种差别不光出现在不同的湍流模型之间，不同的差分格式下仍有区别。为了观察这种细微的差别，故而定义回流区的发展产长度Re如公式（5）所示，后文基于这个特征长度对不同湍流模型以及差分格式对回流区发展的影响进行分析。

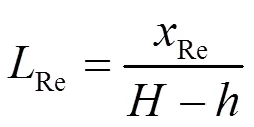
3.2.1 湍流模型对回流区长度的影响

如图4和图5所示分别为流体介质为空气和水时，不同的湍流模型对回流区长度的预测情况。通过观察，当差分方式相同时，在Re数较低时（Re=100），三种湍流模型对回流区长度的预测基本相同，显示出较好的稳定性，但是当Re数增加到1000时，三种湍流模型逐渐出现差异，标准-小于RNG-小于Realizable-。当流动介质为空气时这种逐渐变化的过程较为清晰。而当介质为水时，Re=500工况下，这种规律性较弱，但是总体上仍是上述规律。

图4 介质为空气时不同湍流模型下回流区的长度

图5 介质为水时不同湍流模型下回流区的长度

3.2.2 不同差分格式对回流区长度的影响

图6和图7分别是流体介质为空气和水时，不同差分方式对回流区长度的预测情况。通过观察可以发现，流体介质为空气时，二阶迎风与QUICK方式较为接近，一阶迎风与前两者相差较为明显，表现为：当Re=100时，一阶迎风值大于二阶迎风和QUICK方式，当Re=500时，一阶迎风小于其他二者。而当Re=1000时，变化出现差异，在标准-模型下，一阶迎风小于其他二者，而在RNG-和Realizabl-湍流模型下一阶迎风预测值又大于其他两者。

当流体介质为水时，几种差分方式对回流区长度的影响规律性较弱，主要表现为：Re=100时，三种差分方式预测的回流区长度差异较小；当Re=1000时，二阶迎风和QUICK方式的差异较小，而一阶迎风方式小于前面两者。而当Re=500时，规律性较弱主要表现为一阶迎风方式的预测值小于其余两者。

图6 介质为空气时不同差分方式下回流区的长度

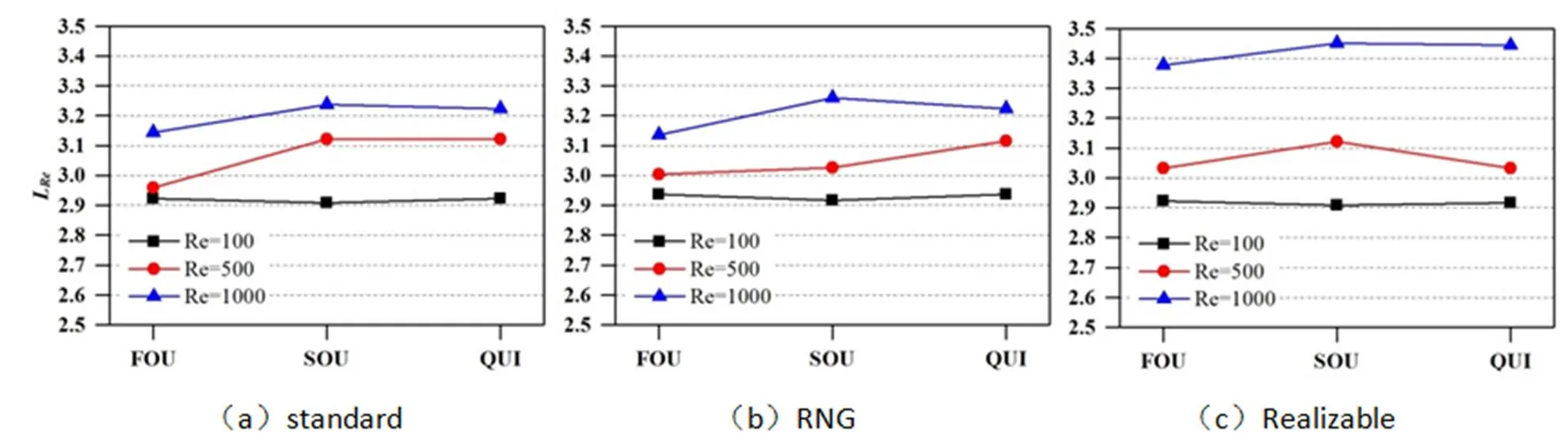
图7 介质为水时不同差分方式下回流区的长度

3.3 对湍流强度发展的影响

湍流强度简称湍流度或湍强，是湍流强度涨落标准差和平均速度的比值，是衡量湍流强弱的相对指标，如公式（6）所示。

流场中湍流强度越强与回流区长度有一定的相关性，湍流强度越强回流区长度就越长。后文中，采用流场中湍流强度的峰值来表征流场中湍流发展状态。

3.3.1 湍流模型对湍流强度峰值的影响

图8和图9所示分别为介质为空气和水时不同湍流模型预测的湍流强度峰值。通过观察可以发现当Re=100或500时，无论流体介质是空气还是水，湍流模型的不同对于湍流强度峰值的影响很小，预测值基本相同。而当Re=1000时，开始出现差异，对于空气而言，RNG-模型的预测值较其他两者较小；对于水而言，湍流模型的预测值规律性较差，只有当在一阶迎风差分方式下，呈现出Standard-大于RNG-大于Realizable-的规律，而其他差分方式下差异很小。

图8 介质为空气时不同湍流模型下湍流强度的峰值

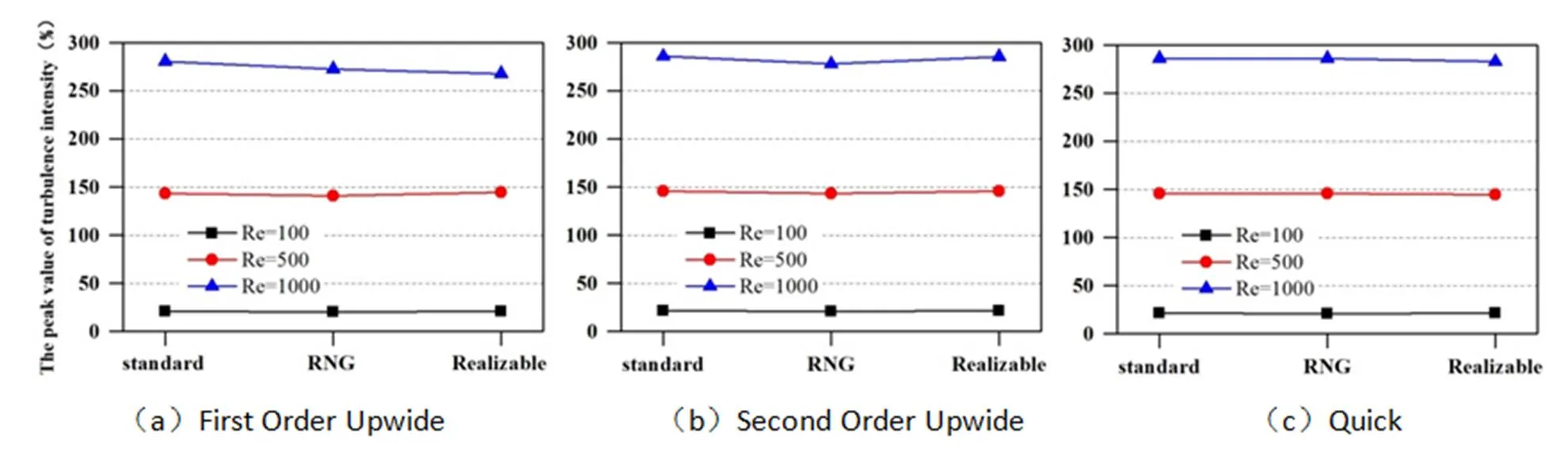
图9 介质为水时不同湍流模型下湍流强度的峰值

3.3.2 不同差分格式对峰值的影响

图10和图11分别为介质为空气和水时不同差分方式下预测的湍流强度峰值。通过观察可以发现当湍流模型为Standard-时，差分方式的不同对于预测湍流强度峰值的影响较小。而且，当Re=100和500时，在另外两种湍流模型下差分方式对其预测值的影响也很小。但是，当Re=1000时，出现场差异，主要表现为：二阶迎风和QUICK方式预测值相近，而一阶迎风差分方式预测值与其相比较小。

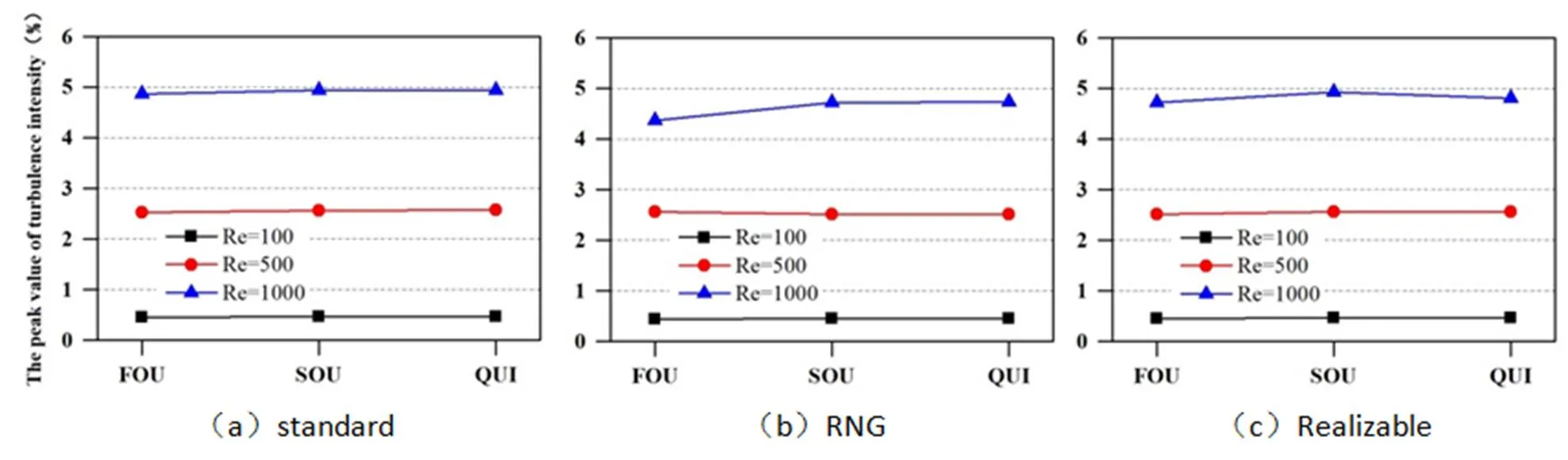
图10 介质为空气时不同差分方式下湍流强度的峰值

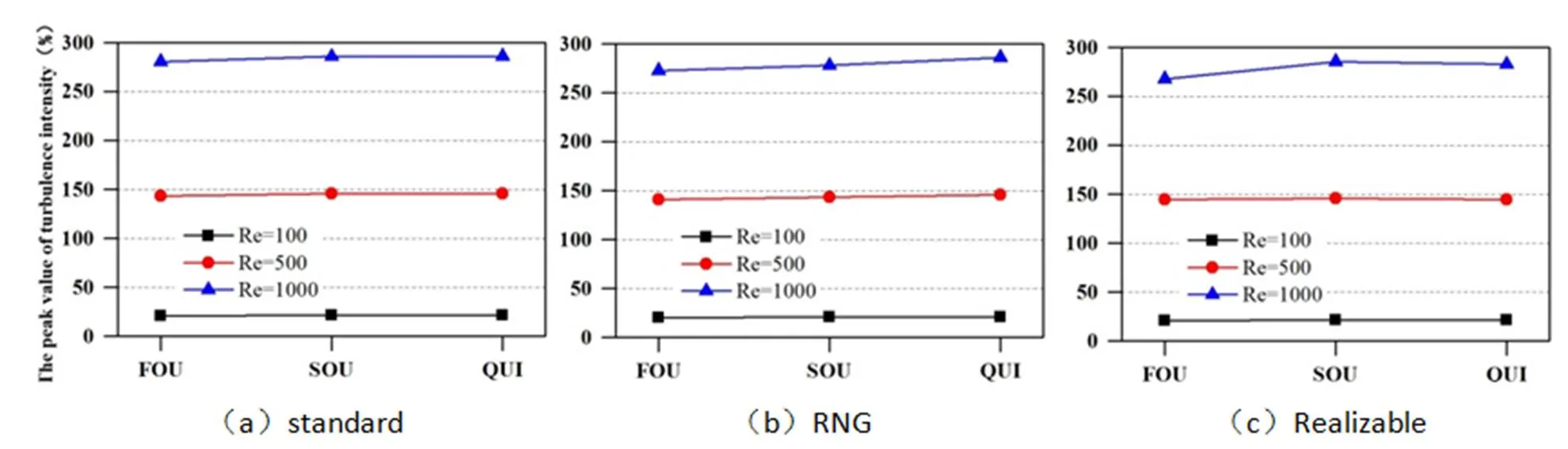
图11 介质为水时不同差分方式下湍流强的度峰值

4 结论

本文采用不同湍流模型以及差分格式对低雷诺数下一个简化的典型流场进行数值模拟预测时候产生的差异进行比较分析，得出如下结论。

（1）在低雷诺数条件下，采用不同的模型设置会产生较大的差异，所以根据实际情况选择合适的湍流模型以及差分格式对于提升流场数值模拟的精度有较大影响。

通过访谈和实验，认为语速缓慢，语音较高适合老年人的学习。但是这部分的课程只能是针对老年人开设的。如同上文所说，不能让受众面扩大。

（2）当入口Re=100时，RNG-湍流模型对于回流区长度以及湍流强度峰值的预测要略大于标准-模型以及Realizable-模型，同时，更高阶的差分格式（二阶迎风格式以及QUICK格式）相近度更高。

（3）当入口Re=500时，对于空气而言，标准-与RNG-的回流区长度以及湍流强度峰值相近度更高，Realizable-模型的预测值则要大于前面两者，同时，二阶迎风差分格式与QUICK的预测值接近。在该入口雷诺数下，对于粘性跟高的水而言，回流区长度以及湍流强度峰值的规律性不强。

（4）当入口Re=1000时，湍流模型对于回流区长度以及湍流强度峰值的预测差异更加明显，对于空气而言为标准-小于RNG-小于Realizable-，而对于水而言，则是标准-与RNG-接近，Realizable-较大。在该Re数下，高阶差分格式（二阶迎风格式以及QUICK格式）的预测值更为接近。

[1] 方平治,顾明,谈建国.计算风工程中基于-系列湍流模型的数值风场[J].水动力学研究与进展A辑,2010,(4): 475-483.

[2] 李琼,持田灯,孟庆林,等.建筑室外风环境数值模拟的湍流模型比较[J].华南理工大学学报(自然科学版),2011, (4):121-127.

[3] Kataoka H, Harimoto K, Nozu T, et al. Cooperative project for CFD prediction of pedestrian wind environment in the Architectural Institute of Japan[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2007,95:1551-1578.

[4] 张楚华,谷传纲,苗永淼.利用修正低雷诺数-模型对管道分离流动的数值研究[J].应用力学学报,1998,(2): 93-97,148.

[5] 陈刚,张月林,高树滋.利用低雷诺数形式的-模型预测管道中的复杂湍流场[J].力学与实践,1991,(4):22-24.

[7] 赵彬,李先庭,彦启森.用零方程湍流模型模拟通风空调室内的空气流动[J].清华大学学报(自然科学版),2001, (10):109-113.

[8] Launder B E, Spalding D B. The Numerical Computation of Turbulent Flows[J]. Computer Methods in Applied Mechanics and Engineering, 1974,3:269.

[9] Yakhot V, Orszag S A, Thangam S, et al. Development of Turbulence Models for Shear Flows by a Double Expansion Technique[J]. Phys Fluids A, 1992,7:1510.

[10] Shih T-H, Liou W-W, Shabbir A, et al. A New Eddy-Viscosity Model for High Reynolds Number Turbulent Flows Model Development and Validation[J]. Computers Fluids, 1995,3:227.

[11] 尹则高,张土乔,黄亚东,等.连续突扩管流的数值模拟[J].流体机械,2005,(8):24-27.

[12] 王小华.突扩流的数值模拟[J].低温建筑技术,2003,(1): 59-60.

Study on the Influence of Different Turbulence Models and Discretization Schemes on the Numerical Simulation of the Typical Flow Field under Low Reynolds Number

Yin Jiefeng1Gao Chunyan2Gao Yiren3

( 1.Xi'an Thermal Power Research Institute Co., Ltd, Xi’an, 710000;2.State Grid Liaocheng Power Supply Company, Liaocheng, 252000;3.Shanxi Gas Group New Energy Development Co., Ltd, Xi’an, 710016 )

Owing to the limitation of turbulence theory and numerical simulation method, it is difficult to predict the flow field under low Reynolds number by using computational fluid dynamic (CFD). In addition, the calculation setting of the models also has a great influence on the final calculation accuracy. In this present study, the author selected the standard, RNG, Realizablethree commonly used turbulence model and the First order Upwind scheme, Second Order Upwind scheme and QUICK scheme three common discretization scheme for simulating a simplified typical flow fields, and then the influence of different simulation settings on the results of flow field calculation were compared and analyzed.

low Reynolds number; turbulence models; discretization Schemes

1671-6612（2017）05-453-07

TU834

A

2016-09-07

作者（通讯作者）简介：殷结峰（1988-），男，硕士，国家注册暖通工程师，E-mail：371554978@qq.com