基于非合作博弈的簇间能量优化路由算法研究
林德钰, 王 泉
(西安电子科技大学 计算机学院,710071 西安)
基于非合作博弈的簇间能量优化路由算法研究
林德钰, 王 泉
(西安电子科技大学 计算机学院,710071 西安)
针对无线传感器网络(WSNs)的簇间路由进行详细研究,指出目前簇间路由中存在的能量耗散不均衡问题. 通过实际例子指出簇间能耗不均的原因,即各个簇头节点的自私性导致数据流量分布不均,进而引发能耗的分布不均. 在此基础之上,提出规范各个簇头节点行为的非合作簇间路由博弈模型,得出并证明该博弈的Nash均衡点(NEP). 然后基于此博弈模型提出本文的路由算法——基于非合作博弈的簇间能量优化路由算法EIRNG. 最后,进行详尽的仿真实验,分别针对网络的能量效率以及网络性能进行横向及纵向对比,实验结果表明,通过引入平衡因子θi,各层簇头可选择最优数据转发量,从而网络中的簇头之间的能量消耗趋于均衡. 与经典分簇算法PEGASIS以及作者前期工作EEREG相比,采用EIRNG时网络生命期可延长分别为74.1%及8.6%. 因此,基于非合作博弈的簇间路由能量优化算法EIRNG可有效地提高能量效率以及提高网络的性能.
无线传感器网络;簇间路由;Nash均衡点;非合作博弈;网络性能
无线传感器网络(wireless sensor networks, WSNs)是由大量具有感知、处理以及路由功能的节点构成的网络系统[1]. 尽管与传统网络节点相比,传感器节点的处理能力、存储容量受到限制,但是它所具有的小体积、低成本使其应用范围相当广泛[2]. 具体来说,传感器可以密集铺设的方式组成网络系统应用于环境监测、军事监测、医疗护理、濒危物种的跟踪以及灾后安全救援等[1-3].
由于大多数的传感器节点采用电池供能,并且在网络部署完毕之后一般不可能或者难以给节点再充电或者补充能量[4-6]. 比如,地震或者火山监测等危险区域、敌军跟踪等应用场景中,给节点补充能量往往是不切实际的. 而当网络中某个或者某些节点能量耗尽时,将会造成网络的分区或者隔离,监测数据无法传输至Sink节点,这就意味着网络生命的终结. 因此,如何减少节点的能量消耗对于以数据为中心的传感器网络而言至关重要. 一般而言,传感器节点的能耗主要在于数据感知、数据处理以及数据通信等方面. 其中,通信模块所消耗的能量是最主要的[4]. 为减少通信模块所消耗的能量,近年来出现不少的路由算法,其中较为普遍也较为有效的是聚簇路由算法. 由于无线传感器具有节点的密集铺设的特点,在相同或者相近的监测区域数据相关性较大,因此聚簇算法通过选取能量较高的节点作为簇头节点来对数据进行压缩来减少冗余数据的发送进而减少能量消耗[7-20]. 其中,有采用随机方式选举簇头节点的方法,如LEACH协议[9],以及按照节点剩余能量进行簇头选举的协议[10-12],也有采用社会经济学原理,比如引入社会福利函数的方法[13].
大部分聚簇路由协议都针对WSNs存在的“Hot Spot Problem”进行详尽的分析,其中有采用均匀分簇的方法,轮转法更换簇头角色,如LEACH以及LEACH-C协议[9]. 然而,大多数文献尚未考虑到簇头在进行数据转发时存在的能耗不均问题,包括本文作者之前的提出的EEREG[14]也仅局限于簇内能效优化. 因此,本文在原来的簇头路由协议的基础之上,对簇间路由不均问题做进一步研究,将非合作博弈论[15]用于规范簇头数据转发过程,实现簇头间的能量均衡,从而进一步延长网络生命期.
本文通过一个简单例子指出簇间能耗不均的事实存在. 提出高能效的簇间路由算法的博弈模型,针对该博弈模型给出Nash均衡点并且给出相应的理论证明. 基于非合作博弈理论提出本文的EIRNG路由算法,该算法可以作为本文作者之前提出的协议的EEREG[14]的补充. 最后,对提出的EIRNG路由算法进行实验仿真,首先定义网络生命期以及其他的能量效率的指标. 并针对能量效率与EEREG以及其他的著名的聚簇路由协议进行对比分析. 验证本协议在能量效率方面的优越性,证实EIRNG能够延长网络生命期.
1 簇间能耗不均问题
如上图1(a)所示,a,b,c和d分别表示簇头节点,其中a,d表示数据源节点,圆圈内部数字表示当前时刻各个几点的剩余能量Ere,同时链路之间的通信能耗已经相应的标示出来. 现在考虑源节点a,d的路由策略,假设节点b和节点c均在a和d的通信范围内. 由于节点的自私性,所以节点a和d的理性偏好都是选择节点b作为转发的下一跳节点. 当节点a和节点d数据传输完毕,各个簇头节点的剩余能量如图1(c)所示,此时节点的能量极差为4.3.
假设现在采取一定策略规范节点的转发行为,使得a和d在数据转发时同时根据自身发送能耗以及接收节点的剩余能量来选择转发量. 如图2所示,这里为简单起见,假设a和d分别采取如下转发策略:d将全部数据转发至b,a将全部数据转发至节点c,数据转发完毕之后,各个簇头剩余能量如图2(c)所示. 由图可知,此时簇头节点的能量极差为2.7,显然比图1小,能耗不均问题有所改善.
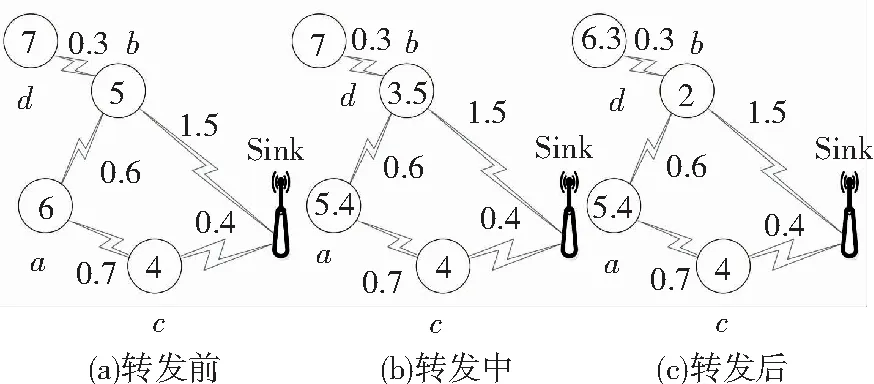
图1 簇间路由能耗不均问题
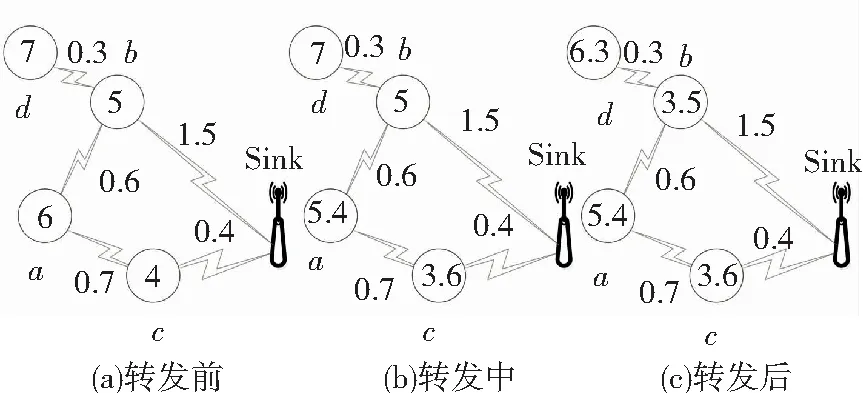
图2 采用一定策略控制簇间路由能耗不均问题
Fig.2 A certain strategy adopted to alleviate the energy consumption imbalance
2 系统模型及相关假设
2.1 能耗模型
本文采用文献[2-5]所采用的一阶无线电模型来描述传感器节点的传输功耗. 具体形式如下式:
erx=bEelec,
(1)
etx=b(Eelec+εampdα).
(2)
式中:erx和etx分别表示节点接收、发送bbit数据所消耗的能量;Eelec表示发送与接收电路发送或者接收单位bit数据所消耗的能量;εamp表示放大电路能耗以及d表示传输距离;α代表衰减系数. 一般而言,α取值可在2~4之间. 为降低能耗,本文控制节点传输半径不大于87米[9],使其为2. 由此能耗模型可看出,当通信半径固定时,节点的通信能耗取决于节点的数据量,所以可通过规范数据通信流量分布来实现能耗的均衡,这正是本文的出发点.
2.2 网络模型
图3所示为本文采用的网络模型,整个区域为一扇形区域,Sink节点位于圆心处. 假设整个区域可分为k个扇形环. 每个扇形环之间的间隔是d. 另外,整个网络模型只是为本文论证方便,具体算法可适用圆形,长方形等一系列其他形状.
2.3 相关假设
所有传感器节点一经铺设之后,均保持静止,并且具有相同的初始能量.
网络拓扑见图3,其模型可进一步扩展,整个监控区域可以是圆形或者正方形或者其他任意形状. 整个网络采用分层次的拓扑,每层之间的距离为87 m,这可以保障节点的数据传输属于自由空间传输模型.

图3 网络模型
每个传感器节点可以调整自己的传输半径,但传输半径小于87 m.
Sink节点与普通节点相比具有无限数据处理能力、存储容量,以及具有无限制的能量.
假设网络报文可无限分割且可以分割成无限小,并且以网络拓扑中的任意一扇形环中的所有节点作为研究对象.
3 基于非合作博弈的簇间路由算法
在无线传感器网络中,由于簇头节点的理性以及自私性,所以在转发数据时偏向于选取最不消耗能量的下一跳节点. 根据2.1节的能耗模型可知,传输距离越大,发送能耗越大. 因此,在簇头节点传输数据时,偏向于选取离自己最近的邻居作为下一跳节点. 然而根据第一节的例子可知,从整个网络生命期来看这种选取下一跳的策略未必是最优的. 因此,为克服个体的自私性以达到整体的最优化,可采用博弈论[15]的方法来规范路径的选取.
3.1 博弈模型
如图4(a)所示,非合作博弈中,每个博弈参与者从自己利益出发,选取使得自身利益最大的策略. 在本文中,体现为每个节点理性偏好于发送最大数据量至离自身距离最近的节点. 这会导致很多节点向同一节点发送过多数据,从而导致该节点的能量提前耗尽. 因此必须制定相应策略来规范每个博弈方的行为. 图4(b)所示的网络模型中,整个网络分为k个层次,每层中所有节点作为博弈参与者,博弈参与者采用的策略是依据一定的效用函数,确定发送至下一层节点的最优通信量,此通信量可使其效用函数最优. 整个网络中的每一层内所有节点均进行相应的单步博弈,这样可在优化能量效率的同时减少网络时延. 本博弈模型如下
(P,S,U).
(3)
在此单次能量优化博弈模型中,把网络拓扑中的任意一层k(1≤n≤k)中所有节点作为博弈模型的参与者,假设第n层中具有的节点数目为N,则参与者集合表示为
P={Pi|1≤i≤N}.
(4)
每个博弈方依据自己的效用函数采取行动,而无需知道其他博弈方的具体策略. 在文中博弈参与者所采取的策略为控制发往上一层(k-1)中的某个节点的数据量. 根据前面分析可知,通过合理规划数据量的发送可有效提高能量效率. 因此,博弈参与者的策略集为
S=(s1,s2,…,sN).
(5)
其中每个节点的策略为
si=Dij.
(6)
表示节点i向节点j传送的数据量.
节点j的容量为

(7)
其中Ej表示节点j计划用于接收能量的能耗.
3.2效用函数
先定义平衡因子如下
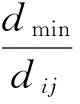
(8)
对于博弈方Pi的收益函数表示如下
).
(9)
式中s-i表示除了节点i之外的所有其他节点的策略. 由式(8)可知道,该效用函数同时考虑了发送节点的发送能耗,以及接收节点j的接收能耗,因此该效用函数可以较好地平衡能量消耗.
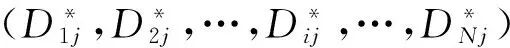
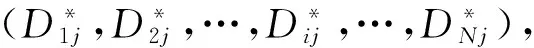
(10)
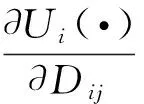
(11)
令i取所有可能值(1,2,…,N)代入(11)中可得:
(12)
再将(12)代入(11)中,可得:
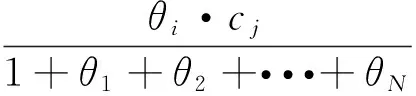
引理3.2第k层任意博弈方i向邻居层k-1节点j所发送的数据量由两者之间的能耗决定,并且当所有博弈方与节点j通信能耗相同时,所有节点发送等量的数据包是本博弈的Nash均衡点.
证明由式(2)可知,节点单位数据的发送能耗由传输距离决定,同时根据式(8)可知,平衡因子θi与传输距离相关,再由式(12)可知,博弈的Nash均衡点由影响因子θi决定,所以每个博弈方发送的最优数据量由其发送能耗决定. 特别地,当所有博弈方的发送能耗相同时,即所有节点i(1<=i<=N)与节点j等距时,θ1=θ2=…=θN,此时,所有节点发送等量数据至j(1<=j<=M)节点.
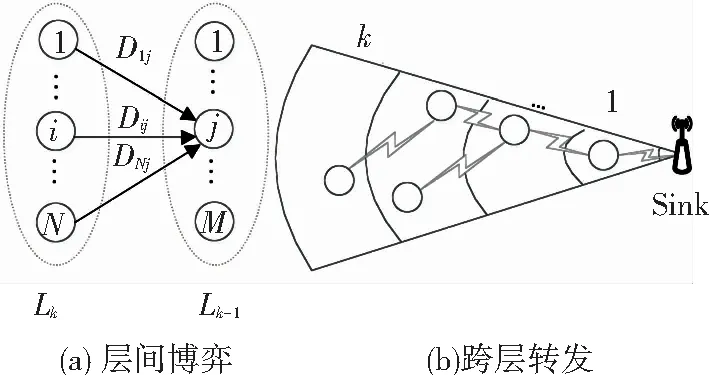
图4 非合作博弈模型
从引理3.1和3.2可知,本文的非合作博弈模型存在Nash均衡点,并且可看出节点发送的数据量既考虑到发送节点的发送能耗,同时也顾及到接收节点的接收能耗. 得出的最佳策略是由平衡因子θi以及cj的函数,其中平衡因子θi代表发送节点的发送能耗,cj反映接收节点的接收能耗. 因此,该模型能很好的解决簇头节点的能耗不均衡问题. 特别地,当各博弈方到特定接收节点的发送能耗相同时,他们发送相同数据量,进一步证实本博弈的实际效果.
3.3基于非合作博弈的簇间路由算法EIRNG
根据第3节的模型模型以及引理3.1和3.2,可得出,基于非合作博弈的簇间路由算法EIRNG如下:
在每一轮簇头选举完毕之后,第n层(1≤n≤k-1)的簇头节点j首先根据自身的剩余能量计算自己在本轮通信中所能承受的最大数据容量cj. 然后,簇头节点j将cj以广播的形式发送到前一层,即(n+1)层的所有簇头节点. (n+1)层的所有簇头节点i(1≤i≤N)接收到相应的数据容量值cj,根据收到的信号强度计算自身到达节点j的距离并计算自身的平衡因子θi. 接下来,节点i(1≤i≤N)将自身的平衡因子θi在本层(n+1)内广播. 待所有节点接收到相应的平衡因子之后,第n+1层内的每个节点按照式(12)计算自己的最优数据发送量,并按此值向节点j发送数据包.
一般而言,分簇阶段产生的簇头节点数量相对较少. 如LEACH协议产生的簇头节点为5%,而EEREG[14]产生的簇头节点也仅为6%左右. 因而,每层簇头告知其最大容量cj的广播报文所消耗的能量相对于每轮进行的数据传输量可忽略不计. 同时,由于簇头节点数目有限也不致产生广播风暴现象. 根据文献[21],传感器节点执行1 000条指令所消耗的能量与将1 bit数据发送20米距离相当. 并且每执行一次簇头轮换才执行一次最优通信量的计算. 因此,尽管簇头节点在根据平衡因子确定最优通信量的过程需要消耗一定能量,但整体而言并不会影响非合作博弈簇间路由算法的能量效率. 为比较本簇间路由算法的能量效率,将与前期工作EEREG进行比较,算法除了不采用本文的簇间路由之外,工作机制与EIRNG完全一致. 因此,将两者进行对比,可以很明显的看出EIRNG的能量效率与优势.
4 实验与分析
本文采用NS2进行仿真实验,100个传感器节点独立均匀地分布在为R=100 m的圆形区域内. 节点的初始能量为2 J,接收或者发送1 bit数据节点电路所消耗的能量为50 nJ,εamp取值为13 pJ/bit/m2. 本文将整个网络分成3层,即k取值为3,并且Sink节点位于圆心处. 为全面评价本文提出的基于博弈论的簇间路由算法,先给出相应的物理指标作为本算法的评价标准.
4.1 评价指标
本算法是以提高能量效率为目标,而对于WSNs来说,最能反映能量效率的物理指标为网络生命期. 对于网络生命期,不同的应用场景有不同的定义,本文定义如下3个指标:
首节点能量耗尽时间(FND):表示网络中第一个节点能量耗尽的时间,对于某些应用,特别是在军事检测以及濒危物种跟踪等对数据实时性要求较高的应用中[9]定义首节点能量耗尽时间很有实际意义.
半数节点能量耗尽时间(HND):表示网络中一半节点能量耗尽的时间.
最后一个节点能量耗尽的时间(LND):表示网络最后一个节点能量耗尽的时间.
网络平均剩余能量:表示网络存活节点的平均剩余能量. 对于能效优化算法,网络平均剩余能量可以较好的反映网络能量的耗散速率.
数据总量:在仿真期间网络Sink节点收集到的所有数据. 因为WSNs中所有节点的铺设是用来收集数据的,所以衡量数据总量较具有实际意义. 此外,Sink节点收集的数据总量也叫Sink的吞吐量,反映的是网络性能指标.
相对于能量百分比的吞吐量:对能量耗散一定百分比时Sink收集到的数据总量. 这个指标同时考虑了数据量以及能量消耗. 因此可以较好地反应本算法的能量效率.
由于本文是针对簇类算法的簇间路由算法,因此,最后将实验数据与经典的簇类路由协议DHAC[9]、TEEN[11]、PEGASIS[12]以及作者之前所提出的EEREG[14]进行比较.
4.2 实验结果及分析
图5显示采用5种协议的存活节点数目随仿真时间变化图,从图5可看出,在相同时间内,本文提出的EIRNG协议的存活节点数量明显高于其他4种协议. 特别值得一提的是,EIRNG针对作者之前工作的EEREG的簇间路由协议进行了改进,图5可看出,EIRNG使得网络生命期相应延长了. 本文的网络生命期分别采用4.1节所定义的FND,HND以及LND. 图6显示网络生命期的对比图. 从图6可看出,EIRNG的FND值比PEGASIS提高74.1%,比EEREG提高6.8%;在HND值方面,EIRNG比TEEN提高29.4%,比EEREG提高4.5%;最后EIRNG的LND比TEEN提高了50.3%,比EEREG提高8.6%.
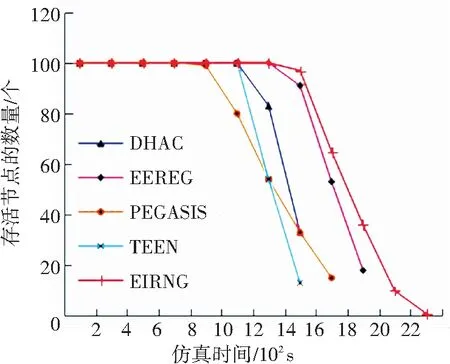
图5 节点数目变化对比
图7反映各协议的网络平均剩余能量对比图. 从图中可看出,采用的EIRNG路由算法之后的节点平均剩余能量明显高于其余4者. 同时也应该看出,与EEREG相比,由于EIRNG在簇间路由协议进行改善,因此,其平均剩余能量比EEREG要高,这也体现了EIRNG的优越性.

图6 网络生命期对比
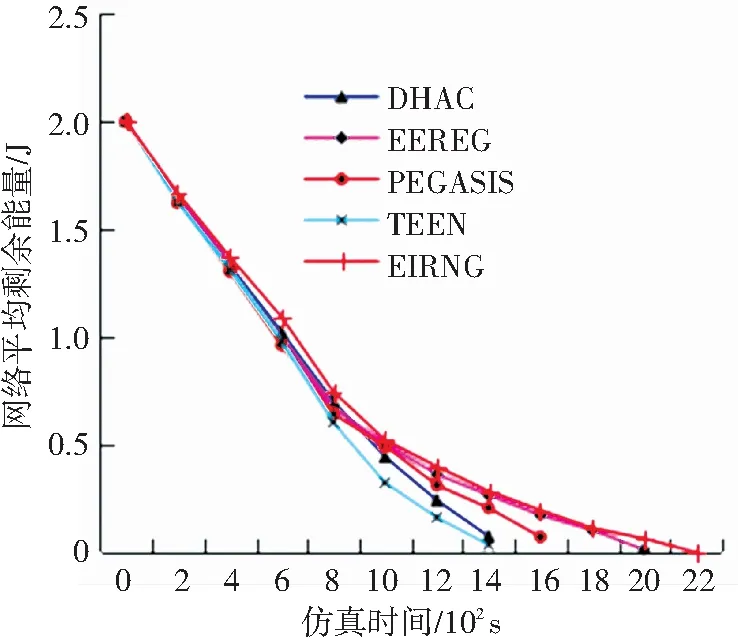
图7 网络平均能量变化
图8显示网络仿真期间,各个Sink节点收集的数据随时间的变化关系图. 从图中可看出,相同时间内,EIRNG收集的数据量是最多的,这主要是由于EIRNG采用了合理的效用函数来规范节点的数据流发送行为,这不仅可以降低网络能耗,而且可降低由于大量数据发往同一个下一跳节点导致的数据包丢失. 同时,由于采用EIRNG网络生命期最长,所以图8显示EIRNG的数据量曲线持续到了最后.
图9显示仿真实验中的各个协议相对能量百分比的Sink所收到的数据量. 可看出,EIRNG的曲线高于其他4者,同时,当网络能量消耗百分之50之后,EIRNG的数据量明显高于其他4种协议. 具体来说,当能量消耗到总能量70%时,EIRNG的数据量比TEEN高出13.2%,同时比EEREG高出2.85%.

图9 相对能量百分率的数据量
5 结 论
WSNs具有一次性铺设、长期使用的特点,加上具体应用场景、环境的限制,给传感器节点再次充电或者补充能量不太现实. 这使得能量受限成为无线传感器网络的固有问题. 本文对聚簇路由协议中的簇间能耗不均问题进行了研究,指出了节点的自私性所引发的的数据流不均是导致簇头间能耗不均匀的根本原因. 在此基础上,提出了基于非合作博弈的簇间路由算法(EIRNG),定义了效用函数以规范簇头间数据转发行为,以实现整个网络拓扑的能量均衡. 最后,通过大量仿真实验,对所提出的EIRNG进行了验证,通过横向与纵向对比表明,本文的EIRNG可以较好地提高能量效率并且获得更高的网络性能.
[1] AKYIDLDIZ I, SU Weilian, SANKARASUBRAMANIAM Y, et al. A survey on sensor networks[J]. IEEE Communications Magazine, 2002, 40(8): 102-114. DOI: 10.1109/MCOM.2002.1024422.
[2] HEINZELMAN, RABINER W, ANANTHA, et al. Energy-efficient communication protocol for wireless microsensor networks[C]//Proceedings of the 33rd Hawaii International Conference on System Sciences. Los Alamitos: IEEE Press, :2000: 8020-8030.
[3] BASAGNI CAROSL A, MELACHRINOUDIS E, et al. Controlled sink mobility for prolonging wireless sensor networks lifetime[J]. Wireless Networks, 2007. 14(6):831-858. DOI: 10.1007/s11276-007-0017-x.
[4] VINCZE Z, VIDA R, VIDACS A. Deploying multiple sinks in multi-hop wireless sensor networks[C]//Proceedings of the 2007 IEEE International Conference on Pervasive Services. Istanbul, Turkey. 2007: 55-63.
[5] BASAGNI S, CAROSI A, MELACHIRINOUDIS E, et al. A new MILP formulation and distributed protocols for wireless sensor netorks lifetime maximization[C]//Proceedings of the 2006 IEEE International Conference on Communications, Istanbul, Turkey: IEEE Press, 2006: 3517-3524.
[6] LIANG W, LUO J, XU X. Prolonging network lifetime via a controlled mobile Sink in wireless sensor networks[C]//Proceedings of the 2010 IEEE Global Telecommunications Conference(GLOBECOM 2010). New York: IEEE Press. 2010:1-6.
[7] DU Xiaojiang, XIAO Yang, DAI Fei. Increasing network lifetime by balancing node energy consumption in heterogeneous sensor networks[J]. Wireless Communication and Mobile Computing, 2008, 8(1): 125-136. DOI: 10.1002/wcm.452.
[8] WEI Dali, JIN Yichao, VUEAL S, et al. An energy-efficient clustering solution for wireless sensor network[J]. IEEE Transations on Wireless Communication, 2011, 10(11): 3973-3983. DOI: 10.1109/GLOCOM.2010.5683095.
[9] PANTAZIS N, NIKOLIDAKIS S, VERGADOS D. Energy-efficient routing protocols in wireless sensor networks: a survey[J]. IEEE Communications survey & Tutorials. 2013, 15(2): 551-591. DOI: 10.1109/SURV.2012.062612.00084.
[10]LUNG C, ZHOU Chenjuan. Using hierarchical agglomerative clustering in wireless sensor networks: an energy-efficient and flexible approach[J]. Ad Hoc networks, 2007, 8(2): 328-344. DOI: 10.1016/j.adhoc.2009.09.004.
[11]MANJESHWAR A, AGRAWAL D. Teen: a routing protocol for enhanced efficiency in wireless sensor networks[C]//Proceedings of the 15thInternational Parallel and Distributed Proceeding Symposium. San Francisco: IEEE Press, 2001: 2009-2015.
[12]LINDSEY S, RAGHAVENDRA C. PEGASIS: power-efficient gathering in sensor information systems[C]//Proceedings of the 2002 Aerospace Conference, DC, USA, IEEE Press, 2002: 1125-1130.
[13]OK C, PRASENJIT MITRA P, LEE S, et al. Maximum energy welfare routing in wireless sensor networks[C]//Proceedings of the 6thInternational IFIP-TC6 Networking Conference. Atlanta: Springer Veriag, 2007: 203-214.
[14]LIN Deyu, WANG Quan, LIN Deqin, et al. An energy-efficient clustering routing protocol based on evolutionary game theory in wireless sensor networks[J].International Journal of Distributed Sensor Networks. 2015, 2015(2015): 1-14. DOI: 10.1155/2015/409503.
[15]XIE Shiyu. Economic game theory[M]. Shanghai: Fudan University Press. 2001. 209-246.
[16]FAROUK F, RIZK R, ZAKI F. Multi-level stable and energy-efficient clustering protocol in heterogeneous wireless sensor networks[J]. IET Wireless Sensor Networks, 2014,4(4): 159-169. DOI: 10.1049/iet-wss.2014.0051.
[17]CHAND S, KUMA R, KUMAR B, et al. NEECP: novel energy-efficient clustering protocol for prolonging lifetime of WSNs[J]. IET Wireless Sensor Networks, 2016, 6(5): 151-157. DOI: 10.1049/iet-wss.2015.0017.
[18]LIN Deyu, Wang Quan.A game theory based energy efficient clustering routing protocol for WSNs[J]. Wireless Networks, 2016,: 1-11. DOI: DOI 10.1007/s11276-016-1206-2.
[19]ZHAO Miao, YANG Yuanyuan, WANG Cong.Mobile data gathering with load balanced clustering and dual data uploading in wireless sensor networks[J]. IEEE Transactions on Mobile Computing, 2015, 14(4): 770-785. DOI: 10.1109/TMC.2014.2338315.
[20]SINGH S, CHAND S, KUMAR B.Energy efficient clustering protocol using fuzzy logic for heterogeneous WSNs[J]. Wireless Personal Communications, 2016, 86(2): 1-25. DOI: 10.1007/s11277-015-2939-4.
[21]DU Xiaojiang, XIAO Yang, DAI Fei. Increasing network lifetime by balancing node energy consumption in heterogeneous sensor networks[J]. Wireless Communications & Mobile Computing, 2008, 8(1): 125-136. DOI: 10.1002/wcm.452.
Researchonenergy-efficientinter-clusterroutingalgorithmbasedonnon-cooperativegame
LIN Deyu, WANG Quan
(School of Computer Science and Technology, Xidian University, Xi’an 710071, China)
Detailed research focusing on the inter-cluster routing for wireless sensor networks (WSNs) is given first. The energy consumption imbalance problem and its cause are presented through a simple example. The paper points out the fact via an example that, the selfish of each cluster head leads to the imbalanced distribution of data flow and the data distribution imbalance then results in energy consumption imbalance. Subsequently, the non-cooperative game model aiming at regulating the behavior of the cluster heads is proposed. The Nash Equilibrium Point (NEP) of the game model is then obtained and proved. According to this game model, an energy-efficient Inter-cluster Routing algorithm based on Non-cooperative Game (EIRNG) is presented, which is the key contribution of the paper. Finally, extensive simulation experiments are conducted and the horizontal and vertical contrast in terms of energy efficiency and network performance are also made. The results show that the cluster heads tend to dissipate energy evenly via determining the optimal amount of the traffic based on a balance factorθi. Compared with the classic clustering routing PEGASIS and the authors’ former work EEREG, the network lifespan can be extended by 74.1% and 8.6% respectively. Therefore, the proposed EIRNG can improve the energy efficiency and the network performance of the network effectively.
wireless sensor networks; inter-cluster routing; Nash equilibrium point; non-cooperative game; network performance
by the Sink
10.11918/j.issn.0367-6234.201612085
TP393
A
0367-6234(2017)11-0095-06
2016-12-15
国家自然科学基金(61572385)
林德钰(1988—),男,博士生;王 泉(1970—),男,教授
王 泉, qwang@xidian.edu.cn
(编辑苗秀芝)

