考虑法向载荷变化的Iwan模型及其特性分析
李东武,徐 超
(西北工业大学 航天学院,西安 710072)
考虑法向载荷变化的Iwan模型及其特性分析
李东武,徐 超
(西北工业大学 航天学院,西安 710072)
为了完整、准确地复现摩擦接触界面间的力学行为和描述其能量耗散特性,提出了一种考虑法向载荷变化的Iwan模型.在连接界面的法向上,该模型采用一个非线性弹簧来描述界面法向载荷变化和间歇性分离的行为,在其切向上则采用原始Iwan模型来描述界面间的微滑和宏滑行为;推导了切法向耦合作用下模型的恢复力和位移关系的表达式,给出了模型运动状态转换点的判据;并以简化的摩擦阻尼器模型为对象,求解了振动系统在简谐激励作用下的动力学响应,讨论了不同激励参数对系统动力学特性的影响.分析表明,当法向载荷为常值时,该模型退化为Iwan模型,从而验证了模型的准确性;该模型考虑了切向微滑行为和法向载荷变化的动态耦合,相比于不考虑法向载荷变化的模型能够更加完善、准确地模拟接触界面间的力学行为及其对系统振动响应预测的影响;连接界面的法向分离不仅会减弱系统的阻尼性能,使得系统动响应很高,而且会增强系统响应的非线性程度,在实际工程应用中应尽量避免.
干摩擦;法向载荷变化;接触;微滑;非线性
航空、航天和机械等工程系统中的复杂结构大多是子部件通过螺栓法兰、过盈配合等连接形式装配而成.振动环境下,连接界面受到周期性外载荷作用,在法向可能出现预紧力振荡、界面分离和碰撞,在切向可能发生黏着、摩擦和滑动等行为.这些行为往往具有非线性、跨尺度、不确定性等特点[1-2].研究表明,连接结构接触界面间的复杂力学行为不仅会造成结构的能量耗散,产生结构阻尼,而且会导致刚度非线性现象,从而影响整个结构的动力学特性[3].
针对上述诸多非线性现象,学者们建立了许多接触模型来复现连接界面间的复杂力学行为.早期,一般采用库伦摩擦模型来建模连接界面的摩擦行为,但由于没有考虑界面微观黏滑行为的影响,计算的连接刚度和界面阻尼特性误差较大[4-5].随着接触力学和摩擦学等学科的发展,许多有物理意义的连接模型被提出来,比如Valanis模型[6]、LuGre刷毛模型[7]和Iwan模型[8].其中,由于Iwan模型更为系统和完善地描述了界面的微观黏滑过程,且模型的参数识别过程简单,因而被广泛关注[9].
最早,Iwan模型采用无限多个Jenkins单元串-并联的方式用以描述土木工程结构的弹塑性迟滞行为.Jenkins单元是一个理想弹塑性模型,它是由一个线性弹簧和一个阻尼滑块串联而成.文献[10]首次将Iwan模型应用于连接界面接触力学行为的研究,并对模型中弹簧滑块单元的临界滑移力的分布函数和能量耗散的关系进行了分析.文献[11]详细推导了滑块临界滑移力均匀随机分布条件下,Iwan模型的恢复力和能量耗散的表达式.Song等[12]在原始Iwan模型的基础上,补充了宏观滑移时的残余刚度,进一步完善了该模型.Segalman[13]改变了原始模型中临界滑移力的分布形式,提出了基于截断幂级数分布的四参数非均匀密度函数,建立了基于该密度函数的四参数Iwan模型.最近,文献[14]在此基础上,提出了基于截断幂律分布和双脉冲函数的六参数非均匀密度函数,并推导了模型恢复力和能量耗散的解析表达式.
上述模型在建模过程中通常假设法向接触载荷为常数,不随时间变化.在振动环境下,连接界面的法向载荷一般是随时间变化的,而临界滑移力的大小与法向载荷的大小直接相关.如果在动力学分析中,不考虑法向载荷的变化及其与切向载荷的动态耦合,将不能完整地模拟界面接触摩擦行为,导致结构动态响应预测结果误差较大.
本文采用线性弹簧模拟法向载荷的变化,将其与Iwan模型结合起来,建立了界面法向和切向恢复力变化的动态耦合关系,提出了一种新的考虑法向载荷变化的Iwan模型,采用数值方法研究了简化的摩擦阻尼器系统的振动行为.针对不同激励环境,从能量耗散和频响特性的角度对含接触摩擦模型的振动系统进行动力学分析,得到了一些有意义的结论.
1 Iwan模型及其恢复力

图2为Iwan模型在周期性激励作用下得到的两种典型的迟滞回线.第1种是a-b-c-d-a所围的面积较小的滞环,此时作用于模型上外激励较小,只使部分阻尼滑块发生滑动,模型在卸载段a-b-c和加载段c-d-a都处于黏滑状态;第2种是a′-b′-c′-d′-a′所围的面积较大的滞环,这种情形下,随着外激励的增大,模型中全部的阻尼滑块都发生滑动,从而出现宏观滑移现象,其中在卸载的前段a′-b′,模型处于黏滑状态,而在卸载的后段b′-c′,模型处于宏滑状态.
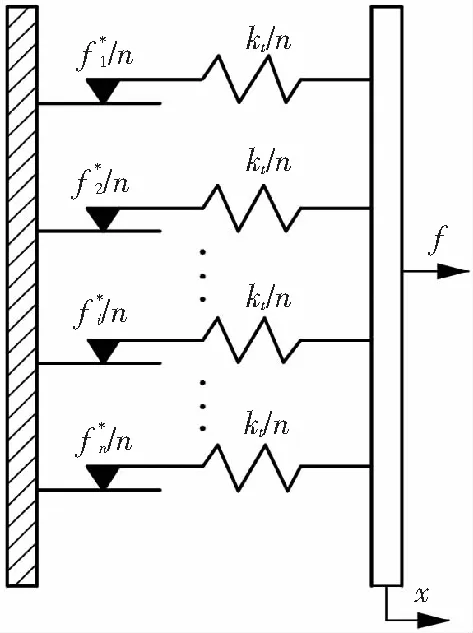
图1 Iwan模型
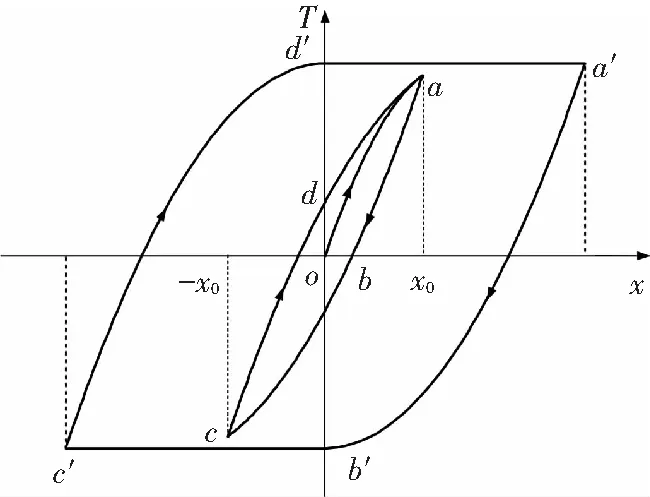
图2 迟滞曲线
骨干曲线oa指首次加载所得的恢复力位移曲线,其表达式为
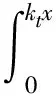
式中φ(f*)为阻尼滑块临界滑移力的分布函数.式(1)中第1项表示模型在滑移状态时阻尼滑块的受力,此时弹簧受力大于阻尼滑块的临界滑移力,阻尼滑块处于滑动状态;第2项表示模型在黏滞状态时弹簧的受力,此时弹簧受力小于阻尼滑块的临界滑移力,阻尼滑块处于静摩擦状态.
通过Masing准则来映射骨干函数,从而获取整个周期内的恢复力表达式.Masing准则表述为

(2)
式中,x0为速度转向时的位移,将骨干函数代入式(2)得到模型加载和卸载段的恢复力-位移关系表达式:
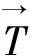
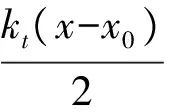
2 考虑法向载荷变化的Iwan模型
Iwan模型中阻尼滑块的临界滑移力与法向正压力满足库伦摩擦定律,其建立了接触面法向与切向的联系.本文的建模思想主要突出切法向的动态耦合,不重点考虑法向的建模方法,因此法向模型采用简单的线性弹簧来模拟法向正压力的变化.
2.1 恢复力-位移关系推导
假定接触面法向的预加常值载荷为Nref,以比例参数的形式给出法向载荷的变化关系为

Iwan模型中阻尼滑块的临界滑移力满足均匀分布规律φ(f*/α)=1/2fy,且其与法向载荷满足库伦摩擦定律fy=μNref,因此分布函数的变化与法向载荷的变化关系相反.
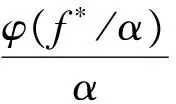
考虑法向模型参数α对切向Iwan模型参数的影响,进而得到模型恢复力-位移关系的骨干函数为

(3)
将Jenkins单元中阻尼滑块的临界滑移力分布函数代入式(3)可得
以下各式中下标()0为速度转向时的参数.当法向载荷变化时,之前使用的Masing准则中的倍数关系将不再适用,需对其进行调整.令xr表示Jenkins单元从阻尼滑块临界滑移状态卸载至弹簧自由状态过程中的弹簧伸长量,xt表示Jenkins单元从弹簧自由状态反向加载至阻尼滑块临界滑移状态过程中的弹簧压缩量,则存在:
x-x0=xr+xt.
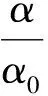
将骨干函数代入调整后的Masing准则可得到模型加载和卸载的恢复力-位移关系表达式:
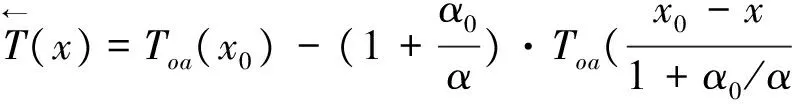
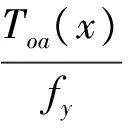
归一化后加载段和卸载段的恢复力-位移关系表达式为:
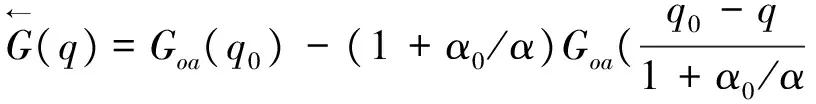
2.2 模型运动状态的判据
周期性激励作用下,模型的运动状态是不断变化的,而各运动状态间相互转变的判据对于正确地描述模型的特性起关键作用.表1给出了模型各种运动状态间相互转变时的判据.

表1 模型运动状态转变的判据
此外,模型从黏滑状态转为宏滑状态的过程中,宏滑状态的判断也是关键步骤.当模型处于黏滑状态时,其恢复力小于阻尼滑块的临界滑移力,而当模型处于宏滑状态时,其恢复力等于阻尼滑块的临界滑移力.因此,在恢复力计算过程中,需要判断恢复力的大小,并将其限制为小于等于临界滑移力,如果不进行此操作,那么将得不到正确的恢复力-位移关系.
当法向载荷小于零时,连接界面发生分离,恢复力归零.需要注意的是,分离状态时,计算程序中状态转换点的判据发生变化,由速度为零的点变为分离状态的末端点.这与连接界面相接触时有所不同.
2.3 准静态过程
本文给出准静态情况下考虑法向载荷变化的Iwan模型预测的滞回曲线,并将不同法向振荡载荷幅值下对应的结果进行对比.计算参数为:切向弹簧总刚度kt=100 kN/m ,法向弹簧刚度kn=100 kN/m,接触面滑动摩擦系数μ=0.1,给定切向位移x=0.5sin(2πt), mm,法向载荷由预加常值载荷N0和振荡载荷N1sin(2πt+δ)两部分叠加而成,其中N0=100 N.图3、4分别给出了切法向激励在同相(δ=0°)和异相(δ=90°)情况下,不同法向振荡载荷幅值下对应的模型迟滞曲线变化的示意图,图例中参数η表示法向振荡载荷幅值与预加常值载荷的比值.
当η=0,此时模型退化为原始Iwan模型.原始的Iwan模型不考虑法向载荷的变化,模型参数在加载和卸载过程保持不变,因此其迟滞曲线是对称的;而考虑法向载荷变化的改进Iwan模型则不同,法向载荷的时变性引起了模型的临界滑移力的变化,从而导致宏观滑动的转折点和宏观滑动行为出现较大差异,其迟滞曲线变为非对称的.因此,是否考虑法向载荷的变化对切向摩擦行为的预测有重要影响.
当η<1,不论法向载荷如何变化,连接界面间总是相互接触的.模型迟滞回线的形状随着法向振荡载荷的变化而变化,其变化规律与切法向的激励形式有关.法向载荷的变化导致模型的宏观滑移力随时间发生变化,从而造成模型各种运动状态的区域发生变化,比如同相激励下,随着η的逐渐增大,迟滞曲线中卸载段表示模型微滑运动状态的区域逐渐增大,表示模型宏滑运动状态的区域逐渐减小;加载段模型微滑运动状态的区域逐渐减小,宏滑运动状态的区域逐渐增大.而异相激励下的变化规律则与之相反.
当η≥1,此时法向载荷会出现小于零的情况,意味着连接界面间会发生间歇性的接触和分离.图3、4中S所指的区域即为η=1.2时模型发生分离的情形,η越大,滞回曲线中分离状态的区域也越大;且分离状态出现的时刻与切法向激励的相位有关.
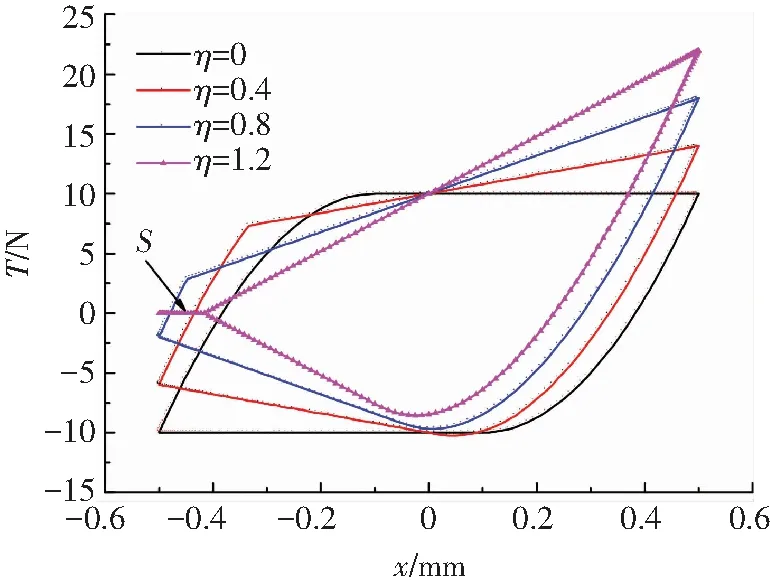
图3 同相时的迟滞曲线
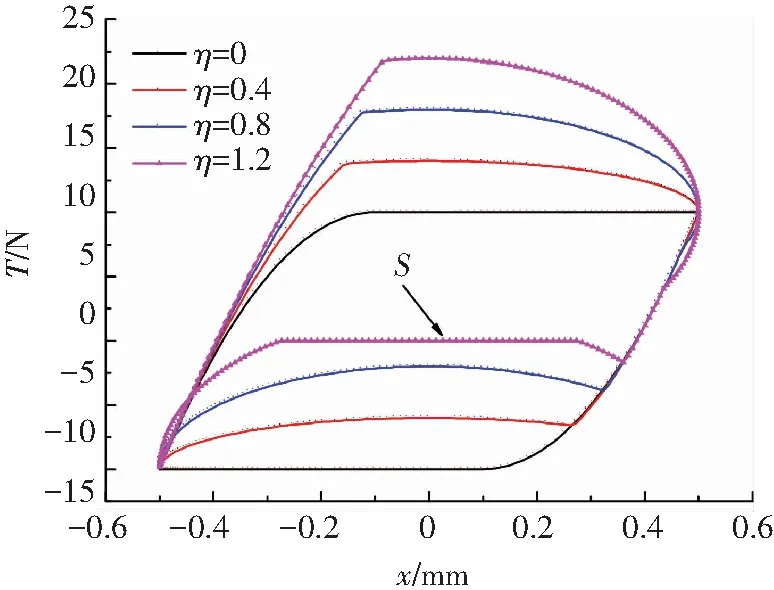
图4 异相时的迟滞曲线
3 系统振动分析
摩擦阻尼器常被用来降低复杂连接结构的振动响应,广泛应用于航空发动机领域.本文建立如图5所示的简化的航空发动机叶片根部摩擦阻尼器模型,利用本文所提出的摩擦接触模型模拟接触面间的力学行为,通过数值仿真的方法研究系统的振动行为.
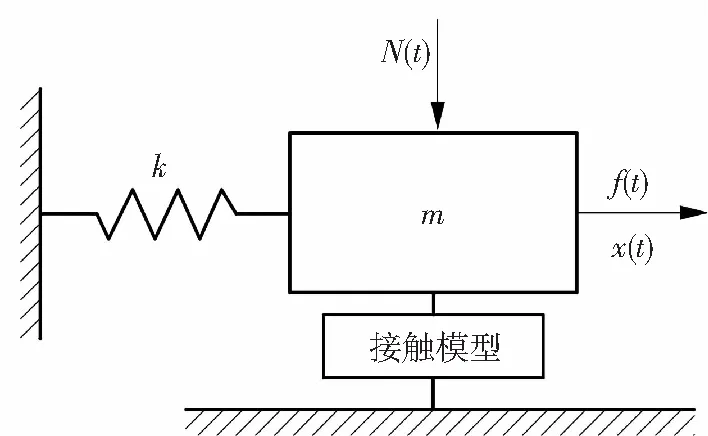
图5 含接触模型的单自由度振动系统
系统参数设为:质量块m=10 kg,刚度k=3.9×105N/m,切向刚度kt=3×105N/m,法向刚度kn=3×105N/m,接触面滑动摩擦系数μ=0.5.系统振动微分方程为

方程两边同时乘以kt/(mfy),得到归一化的方程为
假定法向载荷和切向载荷的形式为:
N(t)=N0+N1sin(ωdt+δ),
F(t)=F1sin(ωdt).
式中:F1为切向载荷的幅值,ωd为切法向载荷角频率.

3个重要的参数:激励频率、切向激励幅值和法向力都会不同程度地影响摩擦阻尼器耗散振动能量的性能[15].因此本文在一定范围内选取上述3种参数的一些特征离散值来研究振动系统的动力学特性.取N0=100 N,相位δ=0°,η取4种典型的情形,分别为N1相对很小的情形η=0.01;适中且连接界面未分离的情形η=0.50;N1适中且连接界面分离的情形η=1.50;和N1相对很大的情形η=10.00,而F1的取值范围则需以激起两个近似线性频率为准.采用数值方法求解摩擦阻尼器系统的动力学方程,对振动系统进行频响分析,结果如图6所示.图6中纵坐标表示正则化后的稳态响应.
首先,研究切向激励对系统动态特性的影响.同一法向振荡载荷作用下,振动系统的频响曲线都表现出典型的非线性特征:随着切向激励幅值的增大,振动系统的刚度出现明显的软化现象,其固有频率从高频向低频渐变,响应峰值先降低后增大.
当β=0.1时,切向激励相对较大,此时模型运动以宏观滑动运动形式为主,系统为近似线性系统,其频率比约为1,系统的动响应很大.
当β=1 000时,切向激励相对较小,模型中大多数滑块处于黏滞状态,系统为近似线性系统,其频率比因连接界面分离而不同,当连接界面未发生分离时,此近似线性频率比为1.33,如图6(a)、(b)所示;而当连接界面分离时,该值将会减小,且法向振荡载荷越小,频率比则越小,如图6(c)、(d)所示.此时,由于大多数滑块都未滑动,导致系统的阻尼性能较差,动响应幅值很高.这两种情况下,接触界面间要么滑移状态占主导,要么黏滞状态占主导,其滞回曲线为一扁平状的环线,近似直线段,因此导致系统耗散的振动能量很小,动响应幅值则很高.
当法向相对正压力适中时,振动系统的迟滞回线比较规则、“饱满”,不存在某一运动状态占绝对主导的情形.相对“饱满”的迟滞曲线所围成的面积也就相对越大,说明其耗散的振动能量越多.
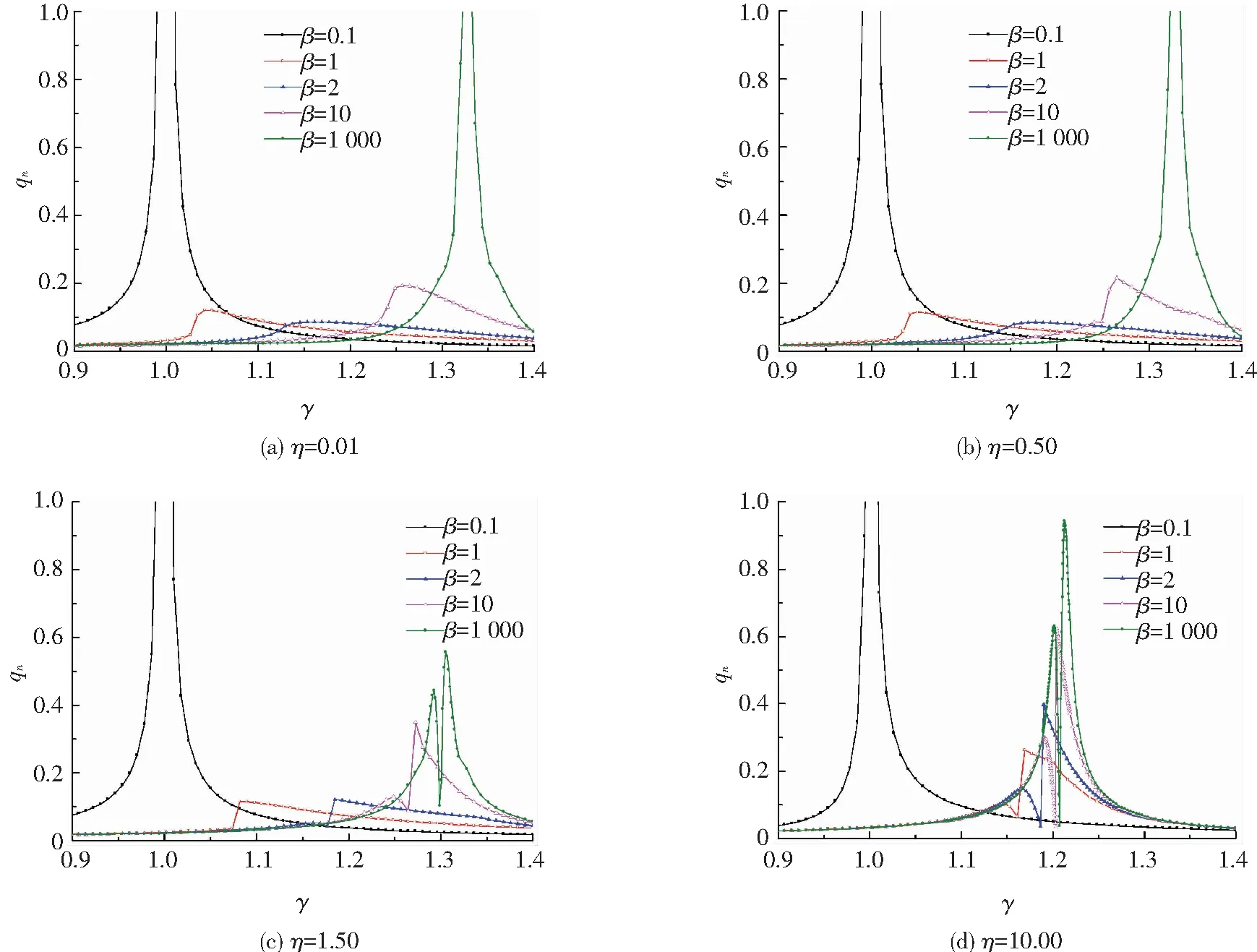
图6 不同激励条件下的频响曲线
再研究法向载荷对系统动态特性的影响.图6(a)、(b)分别是连接界面相接触时的结果,两者较为接近,主要的差异出现在切向激励幅值适中的情形下,同一激励对应的固有频率和响应都会有微小的差异.
当η=1.50时,连接界面发生分离,系统的非线性程度明显增强,频响曲线越加扭曲.当法向振荡载荷适中时,频响曲线出现了“跳跃”,动响应幅值随激励频率的增加出现突然的增大,此时频响曲线可能出现共振峰向低频段偏转的情形,这种现象在实验或者解析解中能够观测到,但是数值计算过程不能复现该现象[16],这就意味着图中的共振峰对应的频率可能略大于其实际峰值频率;此外,当切向激励较小时,频响曲线出现了两个共振峰,且峰值频率比连接界面相接触时小,造成这种现象的原因是界面分离导致的模型运动状态的突变,如图7所示.将切向小载荷下的滞回曲线近似为直线段,其中S表示界面分离状态,箭头表示滞回曲线绘制的路径.图7(a)中模型正向加载至A后,模型的运动状态发生突变,恢复力变为零,连接界面发生分离;而图7(b)则是模型分离但未发生运动状态突变时的示意图.由于模型运动状态的突变,使得模型的非线性程度增强,从而导致振动系统的频响特性复杂化.当η=10.00时,模型的法向振荡进一步增强.随着η的增加,频响共振峰值频率逐渐减小.
在实际的工程结构设计过程中,设计工作者们更加关心的是处于两个近似线性频率之间的频段,在这一频段内,接触界面间的滑动摩擦特性会耗散更多的振动能量,从而为复杂连接结构提供阻尼,降低其动响应幅值.

图7 切向小载荷下连接界面法向分离时的滞回曲线示意
连接界面的法向分离增强了连接结构的非线性程度,造成系统的阻尼性能降低,使得其稳态动响应幅值增大,瞬态过程延长,且瞬态动响应幅值也增大;在某些情形下,可能会发生非常复杂的非线性现象.因此,实际工程中应尽量避免出现法向分离状态或法向振荡载荷过大的情况.
4 相位的影响
给定切向激励幅值和激励频率,改变法向激励的相位来分别求解连接界面在接触和分离状态时振动系统的滞回曲线.图8(a)给出了连接界面接触时的滞回曲线,结果显示,随着法向激励相位的增加,模型滞环中表示卸载段黏滑状态和加载段宏滑状态的曲线都逐渐变长,而表示卸载段宏滑状态和加载段黏滑状态的曲线则逐渐变短.图8(b)给出了连接界面分离时的滞回曲线,图中S表示模型分离状态的区域.分离状态的区域随着法向激励相位的变化而发生变化,有的发生在加载段,有的发生在卸载段,有的则跨越了两个阶段,而且不同激励相位对应的滞回曲线中的分离状态区域的大小也不相同.
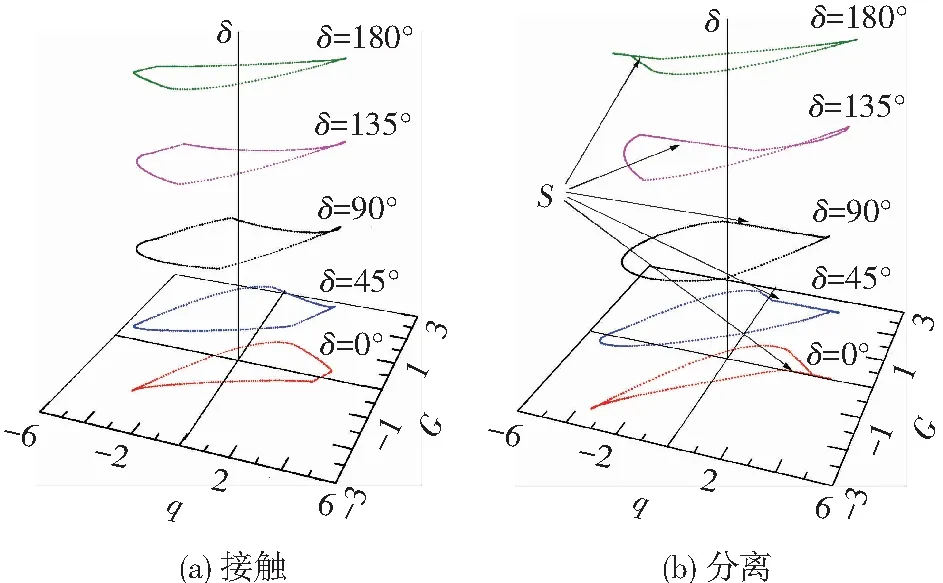
图8 不同相位的滞回曲线
当δ=90°时,滞环所围的面积达到最大,其中表示模型运动状态的曲线长度较为均匀;而当δ=0°和δ=180°时,滞环的面积则最小.法向激励相位通过改变法向力的时域分布来改变模型中阻尼滑块临界滑移力的分布,从而造成滞环中表示运动状态的曲线长度和滞环面积发生变化,随即导致振动系统的阻尼性能变化.
5 结 论
1)本文的模型相比于原始Iwan模型能够更加完善、准确地模拟接触界面间的切法向耦合的力学行为.
2)考虑法向载荷变化与否对连接界面接触力学行为的特性有重要影响.考虑法向载荷变化时,切向恢复力与位移的迟滞回线表现出非对称的特征.
3)通过对简化摩擦阻尼器系统的动力学分析,发现法向载荷幅值变化比对系统的能量耗散特性有重要影响.连接界面的法向分离增强了系统的非线性程度,造成系统的阻尼性能降低,使得其稳态动响应幅值增大,甚至可能会发生非常复杂的非线性现象.
[1] GAUL L, LENZ J. Nonlinear dynamics of structures assembled by bolted joints[J]. Acta Mechanica, 1997, 125(1/2/3/4): 169-181. DOI: 10.1007/BF01177306.
[2] SEGALMAN D J. Modelling joint friction in structural dynamics[J]. Structural Control and Health Monitoring, 2006, 13(1): 430-453. DOI: 10.1002/stc.119.
[3] AMES N M, LAUFFER J P, JEW M D, et al. Handbook on dynamics of jointed structures: SAND2009-4164 [R]. Albuquerque, New Mexico and Livermore, California: Sandia National Laboratories, 2009. DOI: 10.2172/1028891.
[5] MENQ C H, BIELAK J, GRIFFIN J H. The influence of micro-slip on vibratory response,PartⅠ: a new micro-slip model [J]. Journal of Sound and Vibration, 1986, 107(2): 279-293. DOI: 10.1016/0022-460X(86)90238-5.
[6] FERRI A A. Friction damping and isolation systems[J]. Journal of Mechanical Design, 1995, 117(B):196-206. DOI:10.1115/1.2836456.
[7] GAUL L, NITSCHE R. The role of friction in mechanical joints[J]. Applied Mechanics Reviews, 2001, 54(2): 93-106. DOI: 10.1115/1.3097294.
[8] IWAN W D. A distributed-element model for hysteresis and its steady-state dynamic response[J]. Journal of Applied Mechanics, 1966, 33(4): 893-900. DOI: 10.1115/1.3625199.
[9] ARGATOV I I, BUTCHER E A. On the iwan models for lap-type bolted joints[J]. International Journal of Non-Linear Mechanics, 2011, 46(2): 347-356. DOI: 10.1016/j.ijnonlinmec.2010.09.018.
[10]SEGALMAN D J. An initial overview of iwan modeling for mechanical joints: SAND2001-0811 [R]. Albuquerque, New Mexico and Livermore, California: Sandia National Laboratories, 2001. DOI: 10.2172/ 780307.
[11]张相盟, 王本利, 卫洪涛. Iwan 模型非线性恢复力及能量耗散计算研究[J]. 工程力学, 2012, 29(11): 33-39. DOI: 10.6052/j.issn.1000-4750.2011.03.0162.
ZHANG Xiangmeng, WANG Benli, WEI Hongtao. Calculation of nonlinear restoring forces and energy dissipation of iwan model[J]. Engineering Mechanics, 2012, 29(11): 33-39. DOI: 10.6052/j.issn.1000-4750.2011.03.0162.
[12]SONG Y, HARTWIGSEN C J, MCFARLAND D M, et al. Simulation of dynamics of beam structures with bolted joints using adjusted Iwan beam elements[J]. Journal of Sound & Vibration, 2004, 273(1/2):249-276. DOI: 10.1016/S0022-460X(03)00499-1.
[13]SEGALMAN D J. A four-parameter Iwan model for lap-type joints[J]. Journal of Applied Mechanics, 2005, 72(5): 752-760. DOI: 10.1115/1.1989354.
[14]李一堃, 郝志明, 章定国. 基于六参数非均匀密度函数的伊万模型研究[J]. 力学学报, 2015, 47(3):513-520. DOI: 10.6025/ 0459-1879-14-375.
LI Yikun, HAO Zhiming, ZHANG Dingguo. Investigation into iwan model based on the six-parameter non-uniform density function[J]. Chinese Journal of Theoretical and Applied Machanics, 2015, 47(3):513-520. DOI: 10.6025/0459-1879-14-375.
[15]GOLA M M, SANTOS M B D, LIU Tong. Measurement of the scatter of underplatform damper hysteresis cycle: experimental approach[C]// ASME 2012 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Chicago, Illinois: Design Engineering Division, Computers and Information in Engineering Division, 2012: 359-369. DOI: 10.1115/DETC2012-70269.
[16]YANG B D, CHU M L, MENQ C H. Stick-slip-separation analysis and non-linear stiffness and damping characterization of friction contacts having variable normal load[J]. Journal of Sound & Vibration, 1998, 210(4):461-481. DOI: 10.1006/jsvi.1997.1305.
Iwanmodelconsideringvariablenormalloadanditscharacteristicanalysis
LI Dongwu,XU Chao
(School of Astronautics, Northwestern Polytechnical University, Xi’an 710072, China)
To more comprehensively and precisely reproduce mechanical behaviors of frictional and describe properties of energy dissipation, a kind of Iwan model considering variable normal load is developed. In the normal direction, a nonlinear spring is used to describe normal load variation and intermittent separation. In the tangential direction, the original Iwan model is used to describe micro-slip and macro-slip behavior. The relationship between tangential restoring force and relative displacement is derived and the transition criteria among motion states of the model is given. A simplified friction oscillator under harmonic excitation is analyzed to study the effect of different parameters of excitation on the system responses. The proposed model degrades into the original Iwan model when the normal load keeps constant, which validates the model well. This model considering coupling of micro-slip tangential force and variable normal force more comprehensively, exactly reproduces contact interface and effect on the system response. The separation of interface not only reduces damping capability of friction system and makes the responses high, but also strengthens nonlinearity of the system, so it should be avoided in the practical engineering.
dry friction; variable normal load; contact; micro-slip; nonlinear
10.11918/j.issn.0367-6234.201603061
V231.92
A
0367-6234(2017)10-0138-07
2016-03-11
国家自然科学基金委和中国工程物理研究院联合基金资助(U1530139)
李东武(1991—),男,博士研究生;
徐 超(1979—),男,教授
徐 超,chao_xu@nwpu.edu.cn
(编辑张 红)

