单翼损坏下的四旋翼飞行控制器设计
周卫东,储 敏,高 宁, 孙 天
(哈尔滨工程大学 自动化学院,哈尔滨 150001)
单翼损坏下的四旋翼飞行控制器设计
周卫东,储 敏,高 宁, 孙 天
(哈尔滨工程大学 自动化学院,哈尔滨 150001)
针对发生单翼损坏故障时四旋翼飞行器的常规控制失效问题,用反步法设计保证飞行器安全和一般飞行控制的控制器.根据单翼损坏下四旋翼飞行器的旋转与平移运动方程,将控制器划分成内、外环,使用反步法设计这两个环路.内环控制飞行器姿态,外环控制飞行器位置.用反步法设计此种控制器时牺牲飞行器的偏航控制能力,但能实现飞行器一定程度的正常飞行.即能实现飞行器以恒定速度绕其垂直轴转动,机体保持水平同时空间位置不变的近悬停状态,也能通过指令信号实现飞行控制和位置跟踪.经过仿真验证,证实了该控制器对单翼损坏故障下的四旋翼飞行器的飞行控制的有效性,飞行器的稳定性能良好.结果表明,偏航控制能力的丧失不会对四旋翼的安全造成威胁,也不会对飞行器的轨迹跟踪造成较大影响,即保证飞行器能在以恒定速度绕垂直轴转动的情况下进行稳定飞行,同时还能以较快速度跟踪简单的期望轨迹.该研究证实了单翼损坏下的四旋翼飞行器的飞行仍具有可控性.
四旋翼飞行器;单翼损坏;反步法;近悬停状态;飞行控制
四旋翼飞行器具有垂直起降、空中悬停、飞行姿态灵活变换等可操控性,其结构简单并且负载能力较大.其可以通过传感器收集各类信息,已被广泛应用于摄影摄像、军事勘察、天气监测以及救援活动等多个领域.四旋翼的飞行控制研究已发展近二十年,已取得丰硕的成果,如文献[1-3]中实现了四旋翼较高精度的姿态和位置控制,以及实现各种高难度避障、倒飞和复杂轨迹跟踪等动作.四旋翼飞行器是具有强耦合特性的典型非线性系统,一旦发生故障,飞行稳定性就会急剧下降,甚至导致无人机失控.如何保证四旋翼无人机在发生故障的情况下仍能得到有效控制,已成为四旋翼无人机领域的一个热点问题.
目前针对四旋翼的故障检测与隔离已经有诸多优秀成果,文献[4-5]中指出关于观测器的故障检测与隔离技术已经相当成熟,故本文的重点在研究成果较少的单翼损坏故障检测之后的飞行器控制上.对于四旋翼故障下的控制目前已经有很多研究成果,如文献[6]中的滑模控制算法,文献[7]中采用的反步法控制算法,文献[8]中采用的模型预测控制算法,大部分的研究偏向于传感器故障和执行器效率损失.对于执行器损坏故障研究甚少,文献[9]中提出的单翼损坏下的四旋翼飞行控制器采用鲁棒反馈线性化来设计,过程繁琐且计算任务繁重.
针对单翼损坏下的四旋翼飞行器,本文采用反步法来简化控制器设计.文献[10]中指出,四旋翼飞行器为欠驱动、强耦合、非线性、不稳定系统,在机体执行机构出现故障时,其欠驱动度增加,更加不利于飞行器的灵活控制.通过对四旋翼结构和运动机理的分析,滚转角和俯仰角的小变化可以引起位置的较大变化,会使机体失去平衡甚至引起机体撞击地面.而偏航能力的丧失则不会对飞行器的安全造成威胁,而且不会影响飞行器正常的位置控制.所以,采用反步法设计的单翼损坏下的四旋翼飞行控制器,以牺牲四旋翼的偏航控制为前提,解决因为单翼损坏而使得四旋翼欠驱动程度增加的难题,实现此故障下的四旋翼飞行控制.
1 四旋翼飞行器建模
1.1 无故障四旋翼飞行器动力学建模
四旋翼飞行器靠4个电机的转动带动螺旋桨旋转产生升力.文献[11]指出,通过改变不同电机的转速四旋翼可以实现俯仰、滚转、偏航等动作.如图1所示,四旋翼的每个旋翼能产生升力和力矩,两对旋翼(1,3)和(2,4)按相反的旋转方向旋转,以抵消每对旋翼旋转带来的旋转力矩.
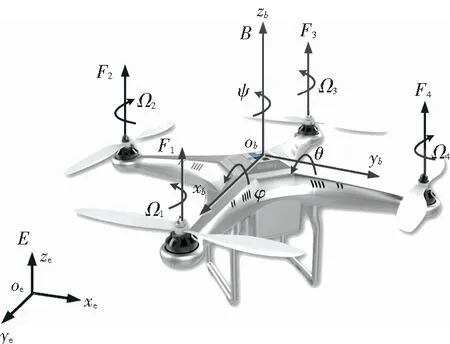
图1 四旋翼飞行器
参照文献[12],分别搭建如图1所示两个右手坐标系,建立以四旋翼重心为原点的机体坐标系B={ob,xb,yb,zb}和标准地球坐标系E={oe,xe,ye,ze}.记四旋翼的姿态角定义在E系中,为Φ=φ,θ,ψ,其中φ、θ、ψ分别为四旋翼飞行器的滚转角、俯仰角和偏航角.则B系可以由E系按x-y-z的旋转顺序得到.
四旋翼在机体坐标系下的角速度ω=[ω1,ω2,ω3]T与在姿态角Φ=(φ,θ,ψ)的关系如下:
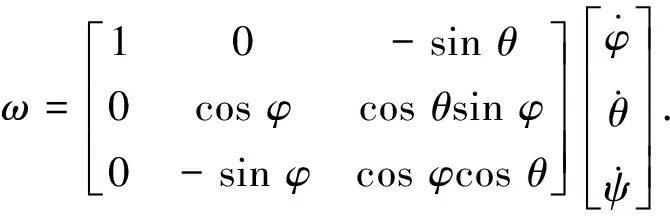
(1)
参照文献[13],将4个旋翼的电机模型定义为
(2)
式中:Fi为各旋翼所受到的升力;Kf为升力系数;Ωi为旋翼旋转速度.即在忽略空气扰动情况下,视旋翼升力与其旋转速度成正比.
由此可以得到,飞行器在机体坐标系下的总升力为
(3)
根据电机模型,考虑四旋翼飞行器的运动原理,可以建立输入向量为
(4)
在假设飞行器为理想完全对称的刚体的前提下,可近似得到机体的转动惯量矩阵为
I=diagIx,Iy,Iz.
(5)
结合式(1)~(5),由牛顿运动定律,可以得到四旋翼飞行器在地球坐标系下的动力方程如下:
1.2 单翼损坏情况下的故障建模
当飞行器的执行器发生一个旋翼处发动机损坏故障时,基于四旋翼飞行器的结构对称性,不失一般性地假定编号为2的翼受损,无法提供正常的升力.如图2所示,由于2翼的损坏导致其不能提供升力,相当于F2=0.由式(4)可知此时有
up=lF4,
可重新建立输入向量为
(6)

图2 2翼发生损坏故障的四旋翼
当飞行器处于悬停状态下时,为了保证飞行器处于水平状态,由于四旋翼的对称结构和运动机理,需同时取F4=0.由式(6)可知,此时的ur=dF1+dF4=uf*d>0,此式显示不可变号,即悬停状态下不可任意控制偏航角速度.由于四旋翼飞行器突发单翼损坏时,其首要工作是使飞行器尽快达到稳定状态而不至于撞机,故只要能使飞行器的滚转角和俯仰角以及位置得到控制即可保证,所以此时的偏航控制并不是很重要.又由于四旋翼本身为欠驱动系统,4个旋翼转速的输入要给出空间6个自由度的输出,故在一个旋翼损坏时,其欠驱动程度增加,所以此时舍弃偏航控制无非是最好的选择.
对于故障下的飞行器状态空间描述,选择状态量为
x=x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12T=
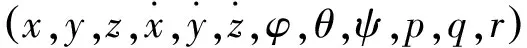
则在单翼损坏故障下的飞行器状态空间表述为:
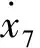
(7)
考虑四旋翼的对称性,选取Ix=Iy.
2 控制器设计
本文的控制器设计建立在单翼损坏的情况视为已经发生的基础上,不做与故障的检测和隔离相关的工作和分析,重点放在故障发生后的系统控制上.
经分析,在2翼损坏的情况下,四旋翼飞行器的欠驱动程度增加,为了使四旋翼在不可避免的单翼损坏情况下能尽量减小损失和保证飞行器不增加外部损坏,本文设计思路为牺牲偏航控制,依赖飞行器无故障的剩余3个旋翼来达到近悬停状态和实现轨迹跟踪.为了解决欠驱动和实现解耦,在四旋翼飞行器的控制过程中,文献[14-15]中,均采用划分子系统来设计控制器,本文也将使用这种方法,将系统划分为内、外环分层控制.设计的内环控制器主要控制飞行器姿态,使单翼损坏的四旋翼飞行器得到稳定的近悬停状态.这里所提到的近悬停状态是指飞行器保证恒定的高度和较稳定的姿态角,同时以一定速度绕垂直轴转动的状态.设计的外环控制器是飞行器位置控制的主体,建立在内环控制器效果良好的基础之上,外环控制器通过期望位置指令信号解算出内环的跟踪姿态信息.
由于飞行器的水平位置向量x,y的加速度为机体所受总升力uf的水平分量提供,而此水平分力的大小受滚转角φ和俯仰角θ的影响.单翼损坏下的四旋翼飞行器的飞行控制器结构如图3所示,水平位置的控制也依赖已经形成的内环控制,所以内环的必要工作是获取滚转角和俯仰角的期望值,以此使飞行器达到期望的水平位置.机体的垂直位置分量z的控制,是通过调节机体总体升力来实现的,需要关注的是,此时还涉及到偏航角旋转速度r.对应于z、uf以及r三者之间的关系以及水平位置控制中涉及到的姿态控制,故在新的位置指令下,内环将从原有的平衡状态达到另一个平衡状态.
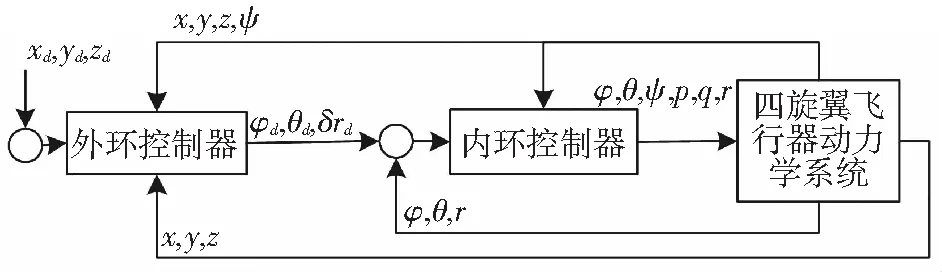
图3 内、外环控制
2.1 内环控制器设计
内环主要用来控制飞行器的滚转角φ、俯仰角θ和偏航角转动速度r,为了解决姿态的耦合问题,选用反步法来设计控制器,使其实现李雅普诺夫意义下的稳定.
设定控制输入为u=[F1,F3,F4]T,选取状态量为
四旋翼飞行器的姿态动力学,即式(7),用上述输入和状态可写成状态空间形式为
式中各矩阵如下:
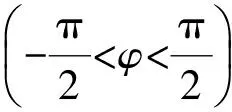
为了使姿态达到期望值,可以通过设计一系列的虚拟控制器来稳定每个状态,用反步法设计的过程如下.
Step1考虑虚拟系统
确定该虚拟系统的跟踪误差为
e1=x1d-x1,
选取Lyapunov函数为
(8)
对式(8)求导有
为了使此虚拟系统稳定,虚拟控制器选为
其中A1为正定阵,此时可得
(9)
Step2考虑虚拟系统
确定该虚拟系统的误差式为
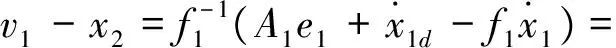
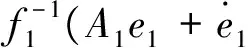
因此可得
选取Lyapunov函数为
求导有
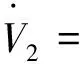
为了使整个内环系统稳定,内环控制器选为
其中A2正定时有
(10)
综上所述,内环控制器为
2.2 外环控制器设计
假定内环是Lyapunov稳定的,且工作在平衡状态,取其工作点为φ→φd,θ→θd,r→rd,且φd和θd是小角度,达到近悬停状态.
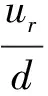
ur=mgd,
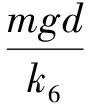
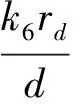
对于水平控制,摘取其位置动力学方程如下
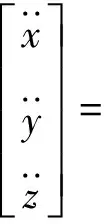
设水平控制系统的输入为
取状态量为
由式(7),可得系统状态空间表达为
其中:
且注意到fψ恒可逆.
用反步法设计外环控制率,推导过程类似内环设计,故在此不做累述,其中,Lyapunov函数设计为:
当设计外环控制率为
可得:
(11)
(12)
式中B1、B2为正定阵,使得外环为Lyapunov稳定.
由于系统的位置控制过程是:外环控制器解算出姿态信息作为内环的输入,通过位置与姿态的耦合关系来实现位置跟踪.在内环渐进稳定的基础上如果外环也是Lyapunov稳定的,则整个系统的输出是稳定的.又根据式(9)~(10)、式(11)~(12)可得,内、外环分别是Lyapunov稳定的.因此,给出有界的系统期望值时,在内外环作用下,四旋翼飞行系统将保持渐进稳定,并且能追踪期望位置和轨迹.本文的仿真结果也说明了这一点.
3 结果和分析
在MATLAB/Simulink中搭建控制系统,对本文提出的反步控制算法进行仿真.实验采用的是微型四旋翼飞行器,模型结构参数见表1.
设定飞行器的起始位置坐标(x0,y0,z0)=(0,0,0),初始姿态角(φ0,θ0,ψ0)=(0,0,0),给定期望位置为(xd,yd,zd)=(2,3,1).
位置和姿态的仿真结果如图4所示.可以看出俯仰角和滚转角在6 s内稳定于稳定值,滚转角和俯仰角的超调量分别为7°和2°,基本满足飞行器的控制性能要求.偏航角速度在波动后趋于恒值.位置控制环无超调量,响应时间约为5 s,在完成位置跟踪之后,飞行器可以在期望位置最终到达近悬停飞行状态.
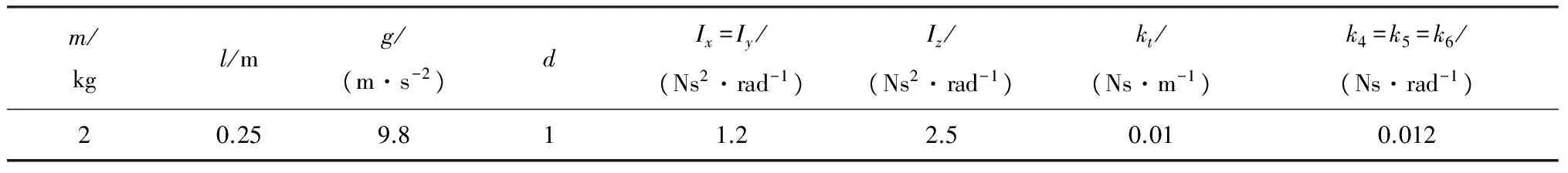
表1 四旋翼飞行器模型参数
上述仿真针对单个目标点的跟踪能力,为了考查控制器对于连续多个目标点的简单路径的跟踪能力,设定多点直线轨迹,验证其跟踪和降落能力.设计4个点为A(0.5,0.5,0.6)、B(1.0,0.5,0.6)、C(1.0,1.0,0.6)和D(0.5,1.0,0.6).期望路径设定为飞行器以路径A→B→C→D→A飞行,然后降落至坐标原点.仿真效果如图5所示,飞行器的飞行轨迹与期望大致重合,简单路径跟踪效果较好.
4 结 论
1)本文针对单翼损坏下四旋翼飞行器,用反步法设计了姿态控制器和位置控制器.该控制器牺牲飞行器的偏航控制,来有效处理失去一个翼的升力情况下,四旋翼的欠驱动程度增加导致姿态和位置不可控的问题.
2)仿真结果说明,偏航控制能力的失去不会对四旋翼的安全造成威胁,也不会对飞行器的正常轨迹跟踪造成较大影响,且保证飞行器能在以恒定速度绕垂直轴转动的情况下进行稳定飞行,同时还能以较快速度跟踪简单的期望轨迹.
3)本文采用的算法对解决在单翼损坏下的四旋翼位置控制和轨迹跟踪具有较强的理论价值,比已有的此类控制器的设计过程更加简单.通过进一步实践探讨,此算法将可用于实际环境中四旋翼突发单翼损坏故障下飞行器紧急降落问题.

图4 姿态控制和位置跟踪仿真
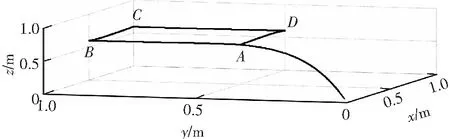
图5 简单路径跟踪和降落仿真
[1] 李毅, 陈增强, 刘忠信. 自抗扰技术在四旋翼飞行姿态控制中的应用[J]. 哈尔滨工业大学学报, 2014, 46(3):115-118. DOI:10.11918/j.issn.0367-6234.2014.03.020.
LI Yi, CHEN Zengqiang, LIU Zhongxin. Attitude control of a quad-rotor robot based on ADRC [J]. Journal of Harbin Institute of Technology, 2014, 46(3):115-118. DOI: 10.11918/j.issn.0367-6234.2014.03.020.
[2] 姜洋. 四旋翼垂直起降机的鲁棒控制问题研究[D]. 哈尔滨:哈尔滨工业大学, 2009.
JIANG Yang.Research of four rotor vertical take-offs and landing aircraft robust control[D]. Harbin: Harbin Institute of Technology, 2009.
[3] 许璟, 蔡晨晓, 李勇奇,等. 小型四旋翼无人机双闭环轨迹跟踪与控制[J]. 控制理论与应用, 2015, 32(10):1335-1342. DOI: 10.7641/CTA.2015.50406.
XU Jing, CAI Chenxiao, LI Yongqi, et al. Dual-loop path tracking and control for quad-rotor miniature unmanned aerial vehicles [J]. Control Theory & Applications, 2015, 32(10):1335-1342. DOI: 10.7641/CTA.2015.50406.
[4] 王恒, 居鹤华, 王玉龙. 不确定飞行控制系统中断故障检测与分离[J]. 控制与决策, 2013,28:1207-1213.
WANG Heng, JU Hehua, WANG Yulong. Actuator outage fault detection and isolation for uncertain flight control systems [J]. Control and Decision, 2013,28:1207-1213.
[5] SHARIFI F, MIRZAEI M, GORDON B W, et al. Fault tolerant control of a quadrotor UAV using sliding mode control[C]// 2010 Conference on Control and Fault-Tolerant Systems. Nice, France: IEEE, 2010:239-244. DOI: 10.1109/SYSTOL.2010.5675979.
[6] ZHOU Qingli, ZHANG Youmin,RABBATH C A, et al. Design of feedback linearization control and reconfigurable control allocation with application to a quadrotor UAV[C]// 2010 Conference on Control and Fault-Tolerant Systems. Nice, France: IEEE, 2010:371-376. DOI: 10.1109/SYSTOL.2010.5675968.
[7] SAIED M,LUSSIER B, FANTONI I, et al. Fault tolerant control for multiple successive failures in an octorotor: Architecture and experiments[C]// Ieee/rsj International Conference on Intelligent Robots and Systems. Hamburg, Germany: IEEE, 2015:40-45. DOI: 10.1109/IROS.2015.7353112.
[8] LANZON A, FREDDI A, LONGHI S. Flight control of a quadrotor vehicle subsequent to a rotor failure[J]. Journal of Guidance Control & Dynamics, 2014, 37(2):580-591. DOI: 10.2514/1.59869.
[9] IZADI H A, ZHANG Y, GORDON B W. Fault tolerant model predictive control of quad-rotor helicopters with actuator fault estimation[J]. IFAC Proceedings Volumes, 2011,44(1):6343-6348.DOI:10.3182/20110828-6-IT-1002.03709.
[10]ZHOU Weidong, ZHU Pengxiang, WANG Changlong, et al. Position and attitude tracking control for a quadrotor UAV based on terminal sliding mode control [C]//Proceedings of the 34th Chinese Control Conference. Hanghou, China:IEEE,2015. DOI: 10.1109/ChiCC.2015.7260164.
[11]LIU Ming, ZHANG Lixian, SHI Peng, et al. Robust control of stochastic systems against bounded disturbances with application to flight control[J]. IEEE Transactions on Industrial Electronics, 2013, 61(3):1504-1515. DOI: 10.1109/TIE.2013.2258293.
[12]SAKTHIVEL R, JOBY M, SHI P, et al. Robust reliable sampled-data control for switched systems with application to flight control[J]. International Journal of Systems Science, 2016, 47(15):3518-3528.DOI: 10.1080/00207721.2015.1090041.
[13]CEN Zhaohui, NOURA H, YOUNES Y A. Systematic fault tolerant control based on adaptive thau observer estimation for quadrotor Uavs[J]. International Journal of Applied Mathematics & Computer Science, 2015, 25(1):159-174. DOI: 10.1515/amcs-2015-0012.
[14]刘锦涛, 吴文海, 李静,等. 四旋翼无人机SO(3)滑模变结构姿态控制器设计[J]. 控制与决策, 2016, 31(6):1057-1064. DOI: 10.13195/j.kzyjc.2015.0560.
LIU Jintao, WU Wenhai, LI Jing, et al. Sliding mode variable structure attitude controller design of quadrotor UAVs on SO(3) [J]. Control and Decision, 2016, 31(6): 1057-1064. DOI: 10.13195/j.kzyjc.2015.0560.
[15]LIPPIELLO V, RUGGIERO F, SERRA D. Emergency landing for a quadrotor in case of a propeller failure: A PID based approach[C]// IEEE International Symposium on Safety, Security, and Rescue Robotics. Hokkaido, Japan:IEEE,2014:1-7. DOI: 10.1109/SSRR.2014.7017647.
Flightcontrolofthequadrotorvehiclewithonerotorfailure
ZHOU Weidong, CHU Min, GAO Ning, SUN Tian
(College of Automation, Harbin Engineering University, Harbin 150001, China)
A design of controller for a quadrotor vehicle with one rotor failure is proposed based on back-stepping approach, to ensure the safety of vehicle when ordinary controllers are ineffective under one rotor failure. According to the rotational and translational motion equations of the quadrotor with one rotor failure, the controller is divided into inner and outer ring. An attitude control loop is adopted to perform the attitude tracking control, and a position loop is proposed to control the position of the vehicle. Although the controller sacrifices the controllability of the yaw state, the vehicle can reach position tracking, and achieve the near-hover flight state in which roll and pitch angles are zero and the angular speed around the vertical axis is a nonzero constant. The simulation results demonstrate the effectiveness of the proposed controller. The results show that the absence of controllability of the yaw state of the quadrotor vehicle will not threaten the aircraft security or its trajectory tracking. The study confirms that a quadrotor vehicle with a rotor failure is still controllable.
quadrotor vehicle; rotor failure; back-stepping approach; near-hover; flight control
10.11918/j.issn.0367-6234.201607010
TP273
A
0367-6234(2017)10-100-06
2016-07-10
国家自然科学基金(61573112)
周卫东(1966—),男,教授,博士生导师
储 敏,yxchumin126@163.com
(编辑张 红)

