隐身反设计下飞翼布局气动与隐身综合设计
张 乐,周 洲,许晓平
(1.中国工程物理研究院 总体工程研究所,四川 绵阳621900;2. 西北工业大学 航空学院,西安710072)
隐身反设计下飞翼布局气动与隐身综合设计
张 乐1,周 洲2,许晓平2
(1.中国工程物理研究院 总体工程研究所,四川 绵阳621900;2. 西北工业大学 航空学院,西安710072)
为同时获得良好的气动和隐身性能,基于双发动机布局下飞翼无人机大鼓包式机身,采用隐身反设计思路,开展了飞翼布局气动与隐身综合设计与分析研究,提出了一种减小翼型前缘半径的机身前缘类“鹰嘴”形飞翼布局优化构型.分别采用CFD(计算流体力学)方法对M6机翼进行气动数值模拟方法验证,以及基于FEKO软件中MLFMM(多层快速多极子方法)和PO(物理光学法)对圆柱体和某飞翼布局缩比模型进行隐身数值计算方法验证,并利用该方法获得了飞翼布局无人机气动与隐身综合特性.结果表明:建立的气动与隐身数值模拟方法计算结果与实验吻合较好,数值计算方法是可靠的;基于隐身反设计思路构建的机身前缘类“鹰嘴”形飞翼布局设计不仅纵向气动特性略微提升,且前向(-25°~25°)隐身性能明显提高,充分表明了隐身反设计思路的有效性;前缘类“鹰嘴”形设计主要影响机身表面压力分布,并有助于提升升阻特性;前缘类“鹰嘴”形设计比传统钝形前缘设计在不同频率和不同滚转角下隐身特性均有所提高.
隐身反设计;飞翼布局;类“鹰嘴”形;气动;隐身
飞翼布局具有高隐身性能与高气动效率,且能够提高突防能力并获取空中优势,因而受到人们越来越多的关注[1],如美国正在研制的X-45[2]、X-47[3]等.为了具备更强的任务能力,飞翼布局常采用大展弦比的方式,如RQ180、RQ170等,这对飞翼布局的设计也提出了更大的挑战.
截至目前,国内外对于飞翼布局开展了大量研究[4].在气动设计方面,Hyoungjin等[5]对一体化翼身融合布局(BWB)进行了详细的气动特性分析;Mialon等[6]、甘文彪等[7]和Liebeck[8]分别针对飞翼构型进行了气动设计及优化研究;鲍君波等[9]进行了飞翼布局气动方案优选和试验验证.对于隐身特性方面,齐红德等[10]开展了飞翼布局隐身特性数值模拟研究;张彬乾等[11]进行了飞翼布局隐身翼型优化设计.而对于气动与隐身综合研究方面,何开锋等[12]开展了基于流体力学和电磁学方程数值求解的飞翼式飞机气动隐身一体化设计研究;Lee等[13]采用并行遗传算法对飞翼无人机开展了气动隐身一体化设计;张德虎等[14]基于双层代理模型开展了飞翼布局气动隐身综合设计;孙奕捷等[15]、Leifsson等[16]则分别结合飞翼布局飞机进行了气动、隐身、控制等多学科优化设计研究.
上述列举以及其他未列举的与飞翼布局相关的研究工作均为飞翼布局无人机的气动和隐身综合设计提供了参考和借鉴,但其主要侧重于小展弦比飞翼布局设计,或单发动机布局下飞翼布局设计研究,而基于大展弦比双发飞翼布局,且在满足无人机内部特殊装载约束条件下(通常采用大鼓包式机身)进行气动和隐身综合设计研究的较少.本文正是基于此,并结合隐身反设计的思路开展气动和隐身综合设计研究与分析.
1 隐身反设计思路下飞翼布局优化构型设计
为了便于清晰地表述飞翼无人机各段翼面组成,如图1所示定义了翼面上各段部件名称.
图1 飞翼布局无人机翼面各部件定义
飞翼无人机一般翼身融合度较高,但在满足任务载荷及内部特殊装载(如卫通、合成孔径雷达)等需求时,且考虑隐身需要,发动机完全深埋于机体内部,在对称面上截面厚度较大,而内翼截面厚度相对较小,导致机身翼面会形成大鼓包.对翼型前缘设计而言,传统设计思路一般是前缘半径较大,这样有助于缓和前缘流动加速情况,逆压梯度相对更小,从而使得较大迎角范围下流动仍是附着的,失速迎角也会增大.综合上述两点,可以开展大展弦比飞翼布局初始构型设计(如图2所示).由图2可看出,初始构型机身前缘曲率较大(前缘呈钝形),由对称截面向内翼截面曲面过渡时曲率变化较大,机身前缘在前向会产生较强的镜面反射,不利于前向隐身,且无人机最主要升力面为外翼和内翼,在保证高升、阻比特性及满足特殊装载约束下,为了进一步缩减前向雷达散射截面(radar cross section,RCS),可仅针对无人机大鼓包机身开展优化修形设计.

图2 飞翼布局初始构型
反设计思路已经非常成熟地应用于飞机气动设计中,在飞翼布局初始构型的基础上,考虑其大鼓包机身会极大降低无人机前向角域RCS,为提升其隐身性能,提出一种基于隐身反设计思路的大展弦比飞翼布局设计.隐身反设计准则是在保持飞翼布局高升阻比前提下,仅对大鼓包机身开展合理的优化修形设计(主要基于钝形前缘),从而改变翼面上电磁散射分布,将机身钝前缘强镜面反射削减为尖顶散射、边缘绕射等弱散射.本文隐身反设计详细思路为:首先,分别开展飞翼无人机初始构型的气动和隐身特性分析;从中提取无人机翼面上强电磁散射源分布;然后,在满足内部特殊装载布置约束下,基于获取的强电磁散射区域,重点针对对称截面、内翼与机身交接截面进行优化修形设计;最终,在满足无人机内部装载约束后,对无人机机身翼面进行一定的曲率控制(为避免形成强镜面反射,曲率尽量保持更平缓的过渡).
基于以上隐身反设计思路,提出了一种减小翼型前缘半径的类“鹰嘴”形前缘设计,建立了飞翼布局优化构型,如图3所示.这种尖前缘设计可以有助于减小无人机前向和侧向RCS,尤其可能会显著提升前向隐身性能.另外,这种前缘设计可能会产生抬头力矩,从而有助于无人机的自配平.但同时,翼型前缘半径的减小,可能会导致气动性能在低速大迎角状态下下降较快,不过在高速下影响可能相对较小,因此,这种前缘设计主要在机身应用.

图3 飞翼布局优化构型
飞翼无人机优化构型与初始构型在机身对称截面、内翼与机身交接面处对比如图4所示,图4中Fw-opt为飞翼布局优化构型,Fw-initial为飞翼布局初始构型.对比可知,飞翼无人机优化构型与初始构型截面弦长不变,隐身反设计思路下将机身前缘由钝形设计为类“鹰嘴”形,前缘曲率半径显著减小,这是本文优化修行设计最重要的部分;另外,在满足机身内部装载约束前提下,优化构型机身对称截面处最大厚度略微下降,且其截面后段厚度略微缩小.考虑到采用减小翼型前缘半径设计时,无人机前缘更易形成流动分离,在低速大迎角状态下气动性能可能会有一定程度恶化,因此,从机身对称截面向内翼过渡时,需要对机身展向截面前缘进行适当的修形.优化修形设计时,为了抑制一定的前缘流动分离,并保证在过渡段(由机身对称截面至内翼与机身交接面)前缘曲率平缓过渡,本文在内翼与机身交接截面采用下表面尖前缘和上表面钝形前缘的组合修形设计.

图4 飞翼无人机初始构型与优化构型两个典型截面对比
Fig.4 Typical section comparison between initial and optimization model of flying wing UAV
2 气动与隐身计算方法及验证
2.1 气动计算方法及验证
针对大展弦比飞翼布局气动数值模拟,计算采用三维雷诺平均可压缩N-S(Navier-Stokes)方程,使用有限体积法对控制方程进行离散,其中无黏对流通量采用Roe格式,黏性通量采用二阶中心差分,湍流模型为k-ωSST.选用ONERA M6机翼绕流场进行气动数值计算方法可靠性验证,参考已有的实验数据[17],考虑到飞翼无人机在飞行状态右边界(如Ma=0.75或Ma=0.70)或大迎角状态下可能会产生较强激波,因而选择相近的亚音速状态进行计算:迎角α=3.06°,马赫数Ma=0.839 5,雷诺数Re=1.172×107.参考实验数据的Ma和Re略高于飞翼布局无人机,但着重关注气动计算方法对于激波强度和位置的捕捉能力.计算采用网格结点为289×65×49的C-H型结构网格,考虑到黏性计算的需要,需保证近物面Y+=1,其中远场边界大小分别为展长和弦长20倍,计算网格如图5所示,在机翼前缘、后和附面层上计算网格都进行了加密处理.
M6机翼气动数值计算结果与实验结果表面压力分布对比如图6所示.对比可知,数值计算在4种典型截面上流动特性与实验结果比较吻合,各截面处激波强度与位置捕捉均较好.整体而言,选取的数值计算方法能够较准确捕捉流场特点,该计算时可靠有效的.

图5 ONERA M6机翼计算网格
对于本文飞翼无人机,气动计算方法与M6机翼计算相同,其中网格剖分仍保证近物面Y+≈1,飞行高度20 km,飞行Ma=0.6,压力远场边界湍流强度为0.2%,湍流黏性比为2,边界条件还包括对称面和固壁等.
2.2 隐身计算方法及验证
大展弦比飞翼布局在不同频段下呈现的电尺寸特性是不同的,本文主要选取L、S、C波段下的典型频率1、3、6 GHz进行隐身计算.国内外对于各种电尺寸目标隐身计算方法主要分为低频积分和高频近似两类.其中低频算法适用于任何激励下的任意几何形状,考虑了各子散射体之间强电磁互耦,能够精确求解任意复杂目标的电磁散射问题,但受计算资源和效率限制,仅适用于电小或电中尺寸计算,而高频近似方法则忽略子散射体之间的电磁互耦,计算精度稍差,适用于高频下计算.本文将采用成熟的商业软件FEKO,并选取MLFMM(多层快速多极子,低频算法)和PO(物理光学发,高频算法)进行计算.为了验证所采用隐身算法的有效性,分别选取圆柱体和某飞翼布局缩比模型进行对比验证,计算坐标系与文献[18]相同.
2.2.1 圆柱体隐身计算方法验证
验证计算选取经典圆柱体金属模型[19],其长度为711 mm,直径为140 mm,计算频率为5.4 GHz,计算角度θ=0°,φ=0°~180°(其中θ为水平面入射角度,φ为俯仰方向入射角度(计算角度坐标系参考文献[18]所示)),计算采用垂直极化方式,网格量约768 86.图7、8给出了圆柱体计算结果与实验结果对比,由图可知,MLFMM和PO算法计算RCS与实验结果吻合较好.另外,MLFMM算法较PO算法在各个入射角度上计算的RCS变化趋势更吻合,其中PO算法计算所得RCS变化曲线较MLFMM方法“零深点”(波谷点)明显更多,这主要因为PO算法会忽略边缘绕射、尖顶散射等而仅仅计算表面的镜面反射,从而导致在局部入射角域RCS会明显偏小.

图6 M6机翼数值计算压力分布与实验结果对比
Fig.6 Pressure distribution comparison between computational and experimental result of M6 wing

图7 圆柱体模型实验与MLFMM算法计算结果对比
Fig.7 Comparison between experimental and computational result with MLFMM of cylinder model

图8 圆柱体模型实验与PO算法计算结果对比
Fig.8 Comparison between experimental and computational result with PO of cylinder model
2.2.2 某飞翼布局缩比模型隐身试验验证
为了验证所采用隐身算法对于大展弦比飞翼布局无人机电磁散射特性计算的可靠性,选取某缩比飞翼模型(与本文飞翼布局初始构型接近)进行测试与计算对比.表1所示为飞翼布局缩比模型实验与仿真计算RCS均值对比(垂直极化).
表1某飞翼布局无人机实验与仿真计算RCS均值对比
Tab.1 Mean value of RCS between experimental and computational result of flying wing UAV

频率/GHz计算方法前向±30°/dBsm全向360°/dBsm计算时间/h1.2实测-7.77-10.33—MLFMM-2.90-9.7075.760PO-0.26-7.570.1383.0实测-0.06-4.15—PO2.86-4.761.6506.0实测1.19-1.42—PO4.70-2.908.150
由表1可知,在频率1.2 GHz下,与实验结果相比,MLFMM算法计算结果比PO算法吻合更好,计算精度也更高,但整体上两种算法RCS值差距不大.尤其随着频率增加,MLFMM算法需要的计算内存剧增且计算时间增长较快,在散射目标电尺寸进一步增加时,PO能够满足一定计算要求,可选择PO算法进行计算.由表1还可知,整体上看,在频率3.0、6.0 GHz下,采用PO算法计算的RCS均值与实验结果还是吻合较好的,能够反映出RCS变化的整体趋势.
对于本文飞翼无人机,隐身计算采用水平极化方式,并采用单站RCS计算,且两种算法都采用三角形面元网格,网格尺寸按照λ/6(λ为入射电磁波波长)划分.
3 结果与分析
3.1 机身前缘类“鹰嘴”形和钝形设计气动性能分析
3.1.1 宏观气动性能结果对比
飞翼布局优化构型和初始构型的纵向基本气动特性对比如图9所示,由图9可知,在迎角-2°~6°内,两种构型升力系数和俯仰力矩系数(力矩参考点为(6 m,0,0))变化为线性的,迎角进一步增大后立即转为非线性;而且还可以看到,在线性段,初始构型的升力系数略高于优化构型,但相应的阻力系数也有所增加,最终表现为优化构型升、阻比略大于初始构型,升、阻特性是变好的,从而也可以反映出隐身反设计思路下的飞翼布局优化构型设计达到了预期的目标.
3.1.2 表面压力分布分析
为了更加详细地分析表面压力变化,选取图10所示3个典型截面位置压力系数进行对比.

图9 飞翼布局优化构型与初始构型纵向基本特性对比

图10飞翼布局3个典型截面位置示意(未完全显示外翼和翼尖)
Fig.10 Three typical spanwise locations of flying wing UAV
飞翼布局两种构型在3个典型截面上压力分布(迎角2°时)对比如图11所示.对比图11(a)、(b)可知,优化构型在机身上两个截面压力变化较明显,也进一步可以看出飞翼布局机身曲面曲率变化较剧烈.由对称面压力分布对比可知,初始构型从前缘到弦向5%之间会形成负升力,这主要是因为其在对称截面位置前缘是稍微向下倾斜的,导致形成的驻点在对称截面的上翼段;而优化构型经过了优化修形设计后在对称截面的前段升力会有所增加.另外,飞翼布局优化构型在对称截面和展向5%截面上弦向中间位置附近后段下翼面压力明显小于上翼面,反映出了典型的反弯翼型翼面压力分布特征.优化构型在截面后段会形成负升力,升力有所下降,不过会产生一定的抬头力矩,有助于飞翼布局进行自配平.
由图11(c)可知,在展向截面18%位置上,两种构型上翼面表面压力分布基本完全相同,而下翼面只在从前缘点到弦向15%处有所差异,这主要是因为两种构型内翼上只在内翼与机身交接截面有所略微不同(参考如图4(b)所示外形对比),而内翼与外翼交界面和整个外翼段是不变的,所以导致了内翼段的表面压力几乎是不变的;另外,由图11还可知,内翼段截面设计时仍保持了反弯翼型表面压力分布的特点,在弦向80%位置附近上、下翼面压力是反向的.

图11 迎角2°下3个典型截面压力分布对比
3.1.3 极限流线分析
飞翼布局无人机优化构型和初始构型上翼面在3个典型迎角下的极限流线分布如图12所示,旨在详细分析飞翼布局翼面上流动发展情况.
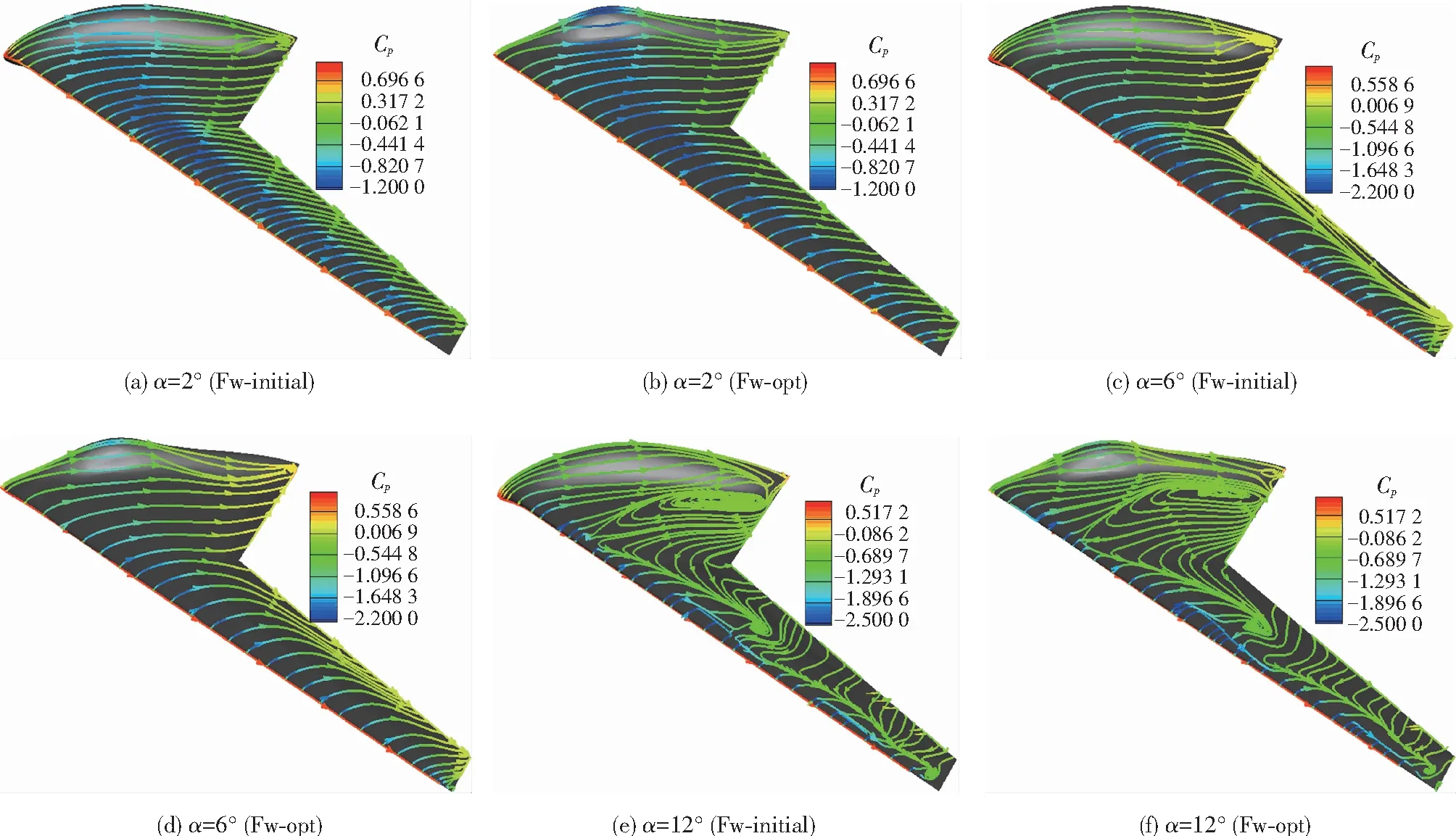
图12 3个典型迎角下两种构型翼面极限流线对比
分析图12(a)、(b)可知,在巡航迎角2°下,飞翼布局两种构型沿顺流方向均基本表现为附着流动,仅仅在机身上极限流线具有一定的偏折,这是因为机身上大鼓包的存在导致其对来流形成一定的阻滞作用;由图12还可知,两种构型在机身上翼面后缘位置附近发生了一定的流动分离,而优化构型流动分离区域更小,其主要是由于后缘表面压力分布造成的,机身大鼓包后段形成的流向压力梯度与机身后掠产生的展向压力梯度相互作用,从而导致了流动分离现象发生在机身后缘压力恢复区.
分析图12(c)、(d)可知,迎角6°下两种构型内翼和外翼后缘分别形成了沿展向反方向(从翼尖到机身对称面)和展向方向的流动.分析图12(c)可知,初始构型在后掠翼展向压力梯度的驱使下,且沿流动方向边界层能量慢慢有所损失,进而使得外翼段后缘翼根位置具有一定的展向流动,但是其流线只是略微有所弯曲.另外,初始构型在外翼段后缘附近已经形成了明显的流动分离,且产生了较清晰的分离线,不过优化构型在外翼后缘处流动分离线显然是靠后的;由此还可看到,翼尖和外翼翼根上仍表现为沿来流方向的附着流动,这是由于受到翼尖涡影响,附近流体之间的掺混会进一步加强,翼尖位置的主流能量也会得到增强,因而克服逆压梯度的能力自然也会提升,最终表现在翼尖流动有所改善.
分析图12(e)、(f)可知,两种构型翼面上分离线随着迎角增大逐渐向前缘方向以及外翼翼根方向移动,当迎角达到12°时,外翼翼面上呈现两条非常明显的分离线,且其靠近翼梢位置的分离线明显更接近前缘位置,另外,靠近外翼翼根的分离线在外翼中段产生小漩涡,而翼尖段呈现了典型的分离螺旋点;同样地,内翼段受到外翼翼根分离区的影响,展向逆压梯度会进一步增大,最终表现在内翼后段产生具有明显的分离旋涡并翼面上具有大面积倒流现象,除了机身,无人机其余翼面流场结构均相当复杂.整体而言,在大迎角12°状态下,飞翼布局两种构型流场特性类似,不过优化构型在外翼翼面上两条分离线比初始构型更加靠后,纵向气动特性更好.
3.2 机身前缘类“鹰嘴”形和钝形设计隐身性能对比
3.2.1 不同频率下隐身特性对比
3个典型频率下飞翼布局优化构型和初始构型RCS对比如图13~15所示.综合图13~15可知,在前向角域0°~25°内(椭圆圈内所示),优化构型RCS较初始构型明显减小,充分体现了隐身反设计思路是有效的.
首先,可以发现,飞翼布局两种构型在不同频率下随着电磁波入射角度变化时整体RCS值变化规律基本保持一致,全向360°角域内均具有6个峰值点,也即在0°~180°角域内有3个强散射点(垂直前缘方向、垂直内翼后缘方向、垂直外翼后缘方向).但是,其虽然形成了3个较强散射峰值点,但飞翼无人机整个翼面上呈现的强散射方向一般都在较集中的方位角上,强散射角域基本都是非常狭窄的,也就导致了在波峰之间的雷达回波信号其实是非常弱的,敌方雷达难以接受到连续的信号,最终也就降低了飞翼无人机被探测到的概率.
其次,当雷达频率增加时,由于前缘强镜面反射的高频效应作用(频率增大,镜面反射强度随之增强),垂直飞翼无人机前缘后掠角方向RCS峰值慢慢增大.显然,由图还可呈现出飞翼布局无人机一定的RCS频率特性变化,随着频率增加,RCS振荡特性有所缓解;以前向角域0°~30°RCS变化为例,飞机RCS频率变化特性可从不同频率下RCS特性展现,其主要原因是当飞翼布局局部尺寸与雷达波长数量级相当,散射目标就在“谐振区”内,随着频率增大,雷达波长逐渐减小,并逐渐远远小于散射目标几何尺寸,然后散射体就会处于“光学区”.

图13 频率1 GHz下飞翼布局初始构型与优化构型RCS对比
Fig.13 RCS comparison between initial and optimization model of flying wing UAV at the frequency of 1 GHz

图14 频率3 GHz下飞翼布局初始构型与优化构型RCS对比
Fig.14 RCS comparison between initial and optimization model of flying wing UAV at the frequency of 3 GHz

图15 频率6 GHz下飞翼布局初始构型与优化构型RCS对比
Fig.15 RCS comparison between initial and optimization model of flying wing UAV at the frequency of 6 GHz
然后,分析同一飞翼布局,以优化构型举例,其在同一雷达波入射角下不同频率时RCS变化规律是不一致的,如1 GHz频率下,入射角58°附近会产生局部小波峰,而在3、6 GHz频率下,在入射角度100°附近才产生小波峰,这是因为入射角58°时电磁散射相干叠加主要由机身前部和机遇前缘形成,而入射角100°时,无人机还具有机身后缘和机翼后缘电磁散射共同叠加,电磁散射也更加复杂,各个局部子散射体在不同角域下的相干散射叠加随着频率变化隐身特性渐渐表现出差异性.
整体上看,建立在隐身反设计思路上设计的优化构型前向RCS(主要为0°~25°)比初始构型明显缩减,不过在其他角域上互有增减,但是RCS变化幅度都非常小,飞翼布局优化构型隐身特性明显更优异.
3.2.2 表面电流分析
飞翼布局优化构型和初始构型在频率1 GHz下局部表面电流对比(电磁波从正前向入射)如图16所示,通过电流分布可分析翼面上各散射区域的分布.

图16 正前向(φ=0°)入射时飞翼布局两种构型表面电流对比
Fig.16 Surface current comparison between initial and optimization model of flying wing UAV at thefront
由图16可知,初始构型表面强电流集中在无人机前缘区域、机头区域、内翼与机身交接面向鼓包最大厚度过渡区域(图16(a)虚线所示),而优化构型则主要集中在飞机前缘区域和机身两侧大鼓包区域(图16(b)虚线所示),整个无人机强电磁散射区域也主要分布在这些方向.通过分析两种构型主要散射源分布区域可知,初始构型在整个钝形前缘区域表面曲率变化剧烈,会形成很强的镜面反射,不过优化构型在机身前缘设计为类“鹰嘴”形,表面曲率明显减小,导致表面电流会主要汇聚于极窄的尖前缘表面,但是同样地,优化构型机身大鼓包向内翼过渡时曲率下降较大,仍然会形成较强反射.整体而言,初始构型翼面上强表面电流区和电流强度都是显著大于优化构型的,这与优化构型在前向RCS缩减是相互对应的(参考表面压力分布分析).
为了定量分析飞翼布局在不同频率和不同角域内隐身性能,表2给出了优化构型和初始构型在水平极化方式下RCS均值对比(前向±20°代表前向-20°~20°角域).由表2可知,优化构型在3个不同角域范围RCS均值与RCS峰值基本上都小于初始构型,其中前向±20°RCS均值下降幅度最明显,这也从定量上进一步反映出隐身反设计思路是有效的.
由表2还可知,对比不同频率下RCS峰值,两种构型峰值都较高(>29 dBsm),这是由于本文飞翼无人机采用大展弦比布局,且前缘呈现单个长条形(仅有一个后掠角),也就导致了前缘方向会累积相当强的雷达散射.再对比前向±20°和±30°角域RCS均值,优化构型在前向±20°角域隐身性能显著优于初始构型,但在前向±30°角域隐身性能却仅略微提升,这是由于垂直前缘(约26°)RCS峰值巨大,基于“湮没”其余入射角下散射;另外,在3个频率下优化构型在前向±20°RCS均值基本接近-10 dBsm,在表面使用纯金属前提下,本文大展弦比飞翼布局隐身性能是非常良好的.
表2水平极化下飞翼布局两种构型RCS均值(不同角域内)
Tab.2 Mean value of RCS between experimental and computational result of flying wing UAV at different azimuth angles (HH)

频率/GHz模型峰值/dBsm前向±20°/dBsm前向±30°/dBsm全向360°/dBsm1Fw⁃initial30.0-3.4315.328.29Fw⁃opt29.4-9.8014.627.743Fw⁃initial33.1-4.4218.3010.70Fw⁃opt32.0-13.0117.139.566Fw⁃initial35.8-4.3620.9513.41Fw⁃opt35.0-12.9720.1012.58
3.2.3 滚转状态下隐身特性对比
飞行器在执行复杂任务时,进入滚转状态有时难以避免,所以完全有必要开展飞翼无人机在不同滚转状态下隐身特性研究.选取飞翼布局右滚转5°(顺时针滚转),计算频率3 GHz,选取雷达波入射角度为θ=-90°,φ=0°~360°(滚装状态下全机左右不对称),并采用水平极化方式.计算方法采用PO算法,网格划分与前文相同,图17给出了飞翼布局优化构型与初始构型在极坐标下RCS对比.
由图17可知,飞翼布局优化构型在前向角域-30°~30°内RCS值明显小于初始构型(虚线框标示),但在其他角域内RCS仅略微互有增减,整体而言,优化构型仍保持良好的隐身特性.另外,飞翼布局初始构型在右滚转5°下全机左侧和右侧入射角度下RCS峰值为22.1、24.0 dBsm,而优化构型则分别为22.0、21.9 dBsm,相比于不滚转状态(表面电流分析中),两种构型RCS峰值减小幅度达到约10 dBsm,这是因为滚转状态下飞机强镜面反射会逐渐减弱引起的.由图17还可知,对于同一飞翼无人机,滚转状态下无人机左右两侧入射方向的隐身性能也存在差异,甚至在局部入射角度上差距较大,如优化构型在入射角度约100°处RCS明显大于约260°处RCS(无滚转时应该相等),这是因为滚转状态下机翼前缘、机身大鼓包等散射相干叠加不同造成的.

图17 飞翼布局优化与初始构型右滚转5°下RCS对比
Fig.17 RCS comparison between initial and optimization model of flying wing UAV at therolling angle of 5°
4 结 论
1)基于隐身反设计思路建立的机身前缘类“鹰嘴”形设计不仅气动特性略微提升,且前向(尤其是前向±25°)隐身性能明显提高,充分表明了隐身反设计思路的有效性.
2)机身前缘类“鹰嘴”形设计主要影响机身段表面压力分布,并会在前缘前段形成抬头力矩,有利于飞机的自配平.
3)机身前缘类“鹰嘴”形设计在不同频率和各个角域内RCS均值较机身前缘钝形设计均有所下降,尤其表现在前向±20°RCS均值明显下降,这主要因为机体表面强电流区明显缩减.
[1] AUSTIN R. Unmanned aircraft systems: UAVS design, development and deployment[M]. New York: John Wiley & Sons Inc., 2010:113-118. DOI: 10.1002/9780470664797.
[2] WISE K A,LAVRETSKY E. Robust and adaptive control of X-45A J-UCAS:A design trade study[C]//Proceedings of the 18th IFAC World Congress. Milano,Italy:IFAC Secretariat,2011:6555-6560. 10.3182/20110828-6-IT-1002.00716.
[3] 张航, 谭慧俊, 李湘萍. 类 X-47 狭缝式进气道的流动特征与工作性能[J]. 航空学报,2009, 30(12): 2243- 2249.
ZHANG Hang,TAN Huijun,LI Xiangping. Flow structure and performance characteristics of X-47-like slot-shaped inlet [J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(12): 2243-2249.
[4] WOOD R M, BAUER S X S. Flying wings/flying fuselage, AIAA-2001-0311[R]. Reston: AIAA, 2001.
[5]HYOUNGJINK, LIOU M S. Flow Simulation of N2B Hybrid Wing Body Configuration,AIAA 2012-0838[R].[S.L.]:AIAA,2012.
[6] MIALON B, FOL T, BONNAUD C. Aerodynamic optimization of subsonic flying wing configurations, AIAA-2002-2931[R]. Reston: AIAA,2002.
[7]甘文彪, 周洲, 许晓平.基于准则的大展弦比飞翼气动设计[J].北京航空航天大学学报, 2015, 41(9): 1608-1614. DOI:10.13700/j.bh.1001-5965.2014.0672.
GAN Wenbiao, ZHOU Zhou, XU Xiaoping. Aerodynamic design of high-aspect-ratio flying wing based on criteria[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(9): 1608-1614. DOI:10.13700/j.bh.1001-5965.2014.0672.
[8] LIEBECK R H. Design of the blended wing body subsonic transport[J]. Journal of Aircraft, 2004, 41(1):10-25.DOI: 10.2514/1.9084.
[9] 鲍君波, 王钢林, 武哲.飞翼布局气动方案优选和试验验证[J].北京航空航天大学学报, 2012, 38(2): 180-184.DOI:10.13700/j.bh.1001-5965.2012.02.021.
BAO Junbo, WANG Ganglin, WU Zhe. Optimization and experimental verification for aerodynamic scheme of flying-wing[J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(2) : 180-184. DOI:10.13700/j.bh. 1001-5965.2012.02.021.
[10]齐红德, 岳奎志, 郁大照. 飞翼隐身特性数值模拟[J].海军航空工程学院学报,2015, 30(3): 258-262. DOI:10.7682/j.issn. 1673-1522.2015.03.011.
QI Hongde, YUE Kuizhi, YU Dazhao. Numerical simulation of the flying wing stealth[J]. Journal of Naval Aeronautical and Astronautical University, 2015, 30(3): 258-262. DOI:10.7682/j.issn.1673-1522.2015.03.011.
[11]张彬乾, 罗烈, 陈真利,等.飞翼布局隐身翼型优化设计[J].航空学报, 2014, 35(4): 957-967. DOI:10.7527/s1000-6893.2013.0429.
ZHANG Binqian, LUO lie, CHEN Zhenli, et al. On stealth airfoil optimization design for flying wing configuration[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(4): 957-967. DOI:10.7527/s1000-6893.2013.0429.
[12]何开锋, 钱炜祺, 陈坚强,等. 基于流体力学和电磁学方程数值求解的飞行器气动隐身一体化设计[J].空气动力学学报, 2009, 27(2): 180-185. DOI: 10.3969/j.issn.0258-1825. 2009.02.007.
HE Kaifeng, QIAN Weiqi, CHEN Jianqiang, et al. Integrated aircraft design of aerodynamic and stealthy performance with numerically solving fluid dynamics and electro-magnetics equations[J]. Acta Aerodynamic Sinica, 2009, 27(2):180-185. DOI: 10.3969/j.issn.0258-1825.2009.02.007.
[13]LEE D S, GONZALE L F, SRINIVAS K, et al. Aerodynamic/RCS shape optimization of Unmanned Aerial Vehicles using Hierarchical Asynchronous Parallel Evolutionary Algorithms[C]//Proceedings of the 24th Applied Aerodynamics Conference. San Francisco: AIAA, 2006.
[14]张德虎,高正红,李焦赞,等. 基于双层代理模型的无人机气动隐身综合设计[J].空气动力学学报,2013, 31(3):394-400.
ZHANG Dehu, GAO Zhenghong, LI Jiaozan, et al. Aerodynamic and stealth synthesis design optimization of UAV based on double-stage metamodel[J]. Acta Aerodynamic Sinica, 2013, 31(3):394-400.
[15]孙奕捷,申功璋. 飞翼布局飞机控制/气动/隐身多学科优化设计[J],北京航空航天大学学报,2009,35 (11):1357-1360.
SUN Yijie, SHEN Gongzhang. Multidisciplinary optimization of control-aerodynamic-stealth for flying wing aircraft design [J]. Journal of Beijing University of Aeronautics and Astronautics, 2009,35 (11):1357-1360.
[16]LEIFSSONL, KO A, MASON W H, et al. Multidisciplinary design optimization of blended wing body transport aircraft with distributed propulsion[J]. Aerospace Science and Technology, 2013, 25(1):16-28. DOI: 10.1016/j.ast.2011. 12.004.
[17]SCHMITT V, CHARPIN F. Pressure Distributions on the ONERA-M6-Wing at Transonic Mach Numbers,AGARD-AR 138[R].[S.L.]:[S.n.],1979.
[18]张乐, 周洲, 许晓平,等. 飞翼无人机3种保形进气口进气道气动与隐身综合特性对比[J]. 航空动力学报, 2015, 30(7): 1651-1660. Doi:10.13224/j.cnki.jasp.2015.07.017.
ZHANG Le, ZHOU Zhou, XU Xiaoping, et al. Comparison on aerodynamic and stealthy performance of flying wing unmanned aerial vehicle with three conformal intake inlets[J]. Journal of Aerospace Power, 2015, 30(7): 1651-1660. DOI:10.13224/j.cnki.jasp.2015.07.017.
[19]阮颖铮. 雷达截面与隐身技术[M]. 北京: 国防工业出版社, 2000.
Integrateddesignonaerodynamicandstealthyofflyingwingunmannedaerialvehiclebasedonstealthyinversedesignmethod
ZHANG Le1, ZHOU Zhou2, XU Xiaoping2
(1.Institute of Systems Engineering, CAEP, Mianyang 621900, Sichuan, China;2.College of Aeronautics,Northwestern Polytechnical University, Xi’an 710072, China)
To obtain both good performance on both aerodynamic and stealthy, integrated design and analysis on aerodynamic and stealthy characteristics for flying wing unmanned aerial vehicle(UAV) is conducted based on stealthy inverse design method, focusing on the big bump in the fuselage of twin-engine layout flying wing UAV. Then a kind of fuselage with leading edge similar to eagle mouth is proposed, whose leading edge radius of airfoil is decreased. Using computational fluid dynamics (CFD) method, the numerical simulation is verified on M6 wing. Physical Optics (PO) and Multilevel Fast Multipole Method (MLFMM) are chosen for numerical study on the stealthy performance of cylinder and a certain scale model of flying wing UAV. Moreover, the verified methods are applied to study the aerodynamic and stealthy characteristics of flying wing UAV. The results show that the aerodynamic and stealthy calculation result is close to the experiment data, indicating that the numerical simulation method is valid. Not only the longitudinal aerodynamic performance of flying wing UAV with fuselage leading edge similar to eagle mouth increases appreciably, but also its stealthy performance improves significantly in the forward direction with the azimuth angle from -25°~25°. In addition, it indicates that the stealthy inverse design method is effective. The design with leading edge similar to eagle mouth mainly affects the pressure distribution of fuselage, and it is helpful to advance the lift/drag characteristic. At the same time, the stealthy performance of the optimize design is better than the traditional blunt leading edge at different frequencies and rolling angles.
stealthy inverse design; flying wing UAV; similar to eagle mouth; aerodynamic; stealthy
10.11918/j.issn.0367-6234.201607022
V211.3
A
0367-6234(2017)10-0022-09
2016-07-07
国家自然科学基金(11302178)
张 乐(1988-),男,博士,工程师;
周 洲(1966-),女,教授,博士生导师
张 乐,568498886@qq.com
(编辑张 红)

