CORDIC算法在波束指向频率补偿中的应用

邹小东， 易 堃， 夏礼诺， 祝伟才

(上海无线电设备研究所， 上海 200090)

CORDIC算法在波束指向频率补偿中的应用

邹小东， 易 堃， 夏礼诺， 祝伟才

(上海无线电设备研究所， 上海 200090)

相控阵天线通过阵内相位梯度的变化实现波束的动态扫描，阵内单元之间的相位梯度由移相器移相产生。为了使数字型移相器在不同频率下实现相同的波束指向，需要对波束指向进行频率补偿；使用CORDIC算法替代查找表算法计算正余弦结果，在误差允许的范围内解决了查找表算法占用资源大的问题，通过MATLAB仿真并进行了FPGA设计和验证。

相控阵天线； 波束指向； 频率补偿

0 引言

相控阵天线具有波束指向灵活、驻留时间可控、波束形状可变等优点。

为了增强相控阵天线的威力，避免单一频点工作的缺陷，跳频、捷变频等应用越来越受到重视并得到推广。为了使相控阵天线在宽频带内具有良好的工作性能，必须解决相控阵天线数字移相器在不同频率下波束指向的频率补偿问题。本文在计算相控阵天线波束指向频率补偿时使用坐标旋转数字计算机(CORDIC)算法替代查找表算法计算正余弦结果，极大地减少了ROM资源的占用，通过仿真及验证证明了该方法的有效性。

1 相控阵天线波束指向频率补偿原理

数字型移相器在不同频率下移相值基本相同(基态不同，可认为是传输线路在不同频率下延迟相位不同造成)。由此在形成波束指向时，相同的阵内相位梯度，在不同频率上将实现不同的波束指向。不同波束指向之间的关系应当满足

(1)

式中：θ1为频率改变前波束指向值；θ2为频率改变后波束指向值。由此可计算频率改变后波束指向值为

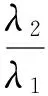
(2)

由此可见，在进行频率补偿时，需要调整波束指向梯度。

若波控机中，已经存储按频率f1计算得到的相位梯度表，则切换至另一个频率f2工作时，需要根据频率f2计算波束在频率f1下的相位梯度分布，使波束实际指向与要求的指向一致。例如，当天线工作在频率f1时，波束指向为θ1；若要天线工作在频率f2时，波束指向为θ2，则应依据频率变化前后的波束指向关系，计算在频率改变前(即频率f1)的波束指向角度，根据此指向角度查找相位梯度表，来实现所需要的波束指向。

(3)

由于在FPGA中计算反正弦比较繁琐，可以利用正弦函数分段计算的方法进行反正弦计算。

令θ=θ′+Δθ，其中θ为波束指向角，θ′为θ的整数部分，Δθ为θ的小数部分，则有

sinθ=sin(θ′+Δθ)

=sinθ′cosΔθ+cosθ′sinΔθ

(4)

式(4)中，当Δθ很小时，有关系式：sinΔθ≈Δθ，cosΔθ≈1，将二者代入式(4)求解得

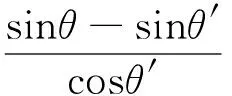
(5)

式中：sinθ满足sinθ′≤sinθ≤sin(θ′+1)，当sinθ给定时，sinθ′,θ′,1/cosθ′均为固定常数。

考虑波束指向在0°～60°的情况，可以按1°为间隔计算角度的正弦值并制表。由于正弦函数在这个范围内为单调函数，故在FPGA中可以利用case语句判断sinθ所处的角度段，再利用式(5)计算出sinθ的反正弦值。

式(5)中的正弦和余弦运算在FPGA中可以通过两种方法来实现：

a) 一种是查找表法，通过脱机计算得到正弦和余弦函数的值并按角度递增的顺序存储在ROM中，根据输入角度值在ROM中查找相应的正弦和余弦值；

b) 另一种是CORDIC算法，通过多次迭代运算逼近所需角度的正弦和余弦值。

查找表法会占用大量ROM资源存储输入角度的正弦和余弦值，以0.01°步进为例，在0°～60°范围内共有6 001个角度，每个角度的正弦和余弦值用16 bit存储则需要的ROM资源为6 001×16×2=192 032 bit；而CORDIC算法则根据输入指向角通过多次迭代运算即可得到输入指向角的正弦和余弦值，并且只需要进行移位和加减运算，能够节省大量资源，因此本文采用CORDIC算法来实现正余弦的计算。

2 CORDIC算法原理

CORDIC算法有两种应用模式—旋转模式和矢量模式。旋转模式是把一个向量旋转一个已知的角度，矢量模式是把一个已知向量定向到与x轴平行。由于本文要计算一个已知角度的正余弦值，因此采用旋转模式。CORDIC算法可以由吉文斯变换(Givens Transformation)导出，如图1所示，假定将直角坐标平面上的向量(x0,y0)旋转角度θ得到向量(x1,y1)，则有

(6)

图1 向量旋转示意图

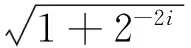
(7)

式中：ki为模校正因子；di代表旋转方向。

当迭代次数趋于无穷时，由式(7)迭代产生的增益为

(8)

通过引入一个角度累加器z来记录旋转的角度，实现对迭代角度的累加。每次旋转的角度通过预先计算得到并存储在查找表中，则角度累加值表达式为

zi+1=zi-diarctan(2-i)

(9)

式中：初始角度z0为旋转角度θ；zi为第i次累加后的角度值；zi+1为第i+1次累加后的角度值；di是由zi决定的符号：若zi<0，di=-1；若zi≥0，di=+1。

式(7)、式(8)、式(9)迭代的最终结果为

(10)

当迭代次数趋于无穷时，输入角度范围为开区间(-99.9°,+99.9°)。而实际往往需要进行闭区间[-180°,+180°]范围内的运算，所以需要对迭代的输入坐标和输出角度进行调整，旋转模式下输入坐标和输出角度的调整方式分别如式(11)、式(12)所示[1]。

(11)

(12)

式中：x0，y0为初始向量的坐标值；x0′，y0′为初始向量坐标值的调整值；zn为n次迭代后的角度累加值；zout为n次迭代后角度累加值的调整值；d是由x0决定的符号：若x0<0，d=-1；若x0≥0，d=+1。

旋转模式下可以同时计算输入角度θ的正弦和余弦值，令x0=1/An，y0=0，z0=θ，则由式(10)可得

(13)

式中：xn,yn为输入角度θ的余弦值和正弦值。

3 占用资源分析

CORDIC算法由式(7)和式(9)通过多次迭代实现，单次迭代只需要进行移位和加减运算，其第i+1级迭代框图如图2所示，其中Xi、Yi、Zi分别为第i级迭代输出的向量坐标和角度累加值，di为第i级迭代输出的符号，在矢量和旋转模式下分别由Yi、Zi决定，“加/减运算”模块是由上一级迭代输出符号di决定的加减运算，“arctan(2-i)”模块通过对每次旋转的角度预先计算并按顺序存储得到。Xi+1、Yi+1、Zi+1、di+1为第i+1级迭代的输出。采用CORDIC算法占用的资源大小与迭代次数及数据宽度有关，而与波束指向角度的步进量无关，因此在步进量更小的情况下能节省更多的ROM资源。本文以采用22级迭代、数据宽度为16 bit为例，占用ROM资源为0，仅需要占用3 073个逻辑单元。与查找表法相比，减少了192 032 bit的ROM资源占用，在波束指向角度步进更小、数据位宽更宽时，资源节省量更为明显。

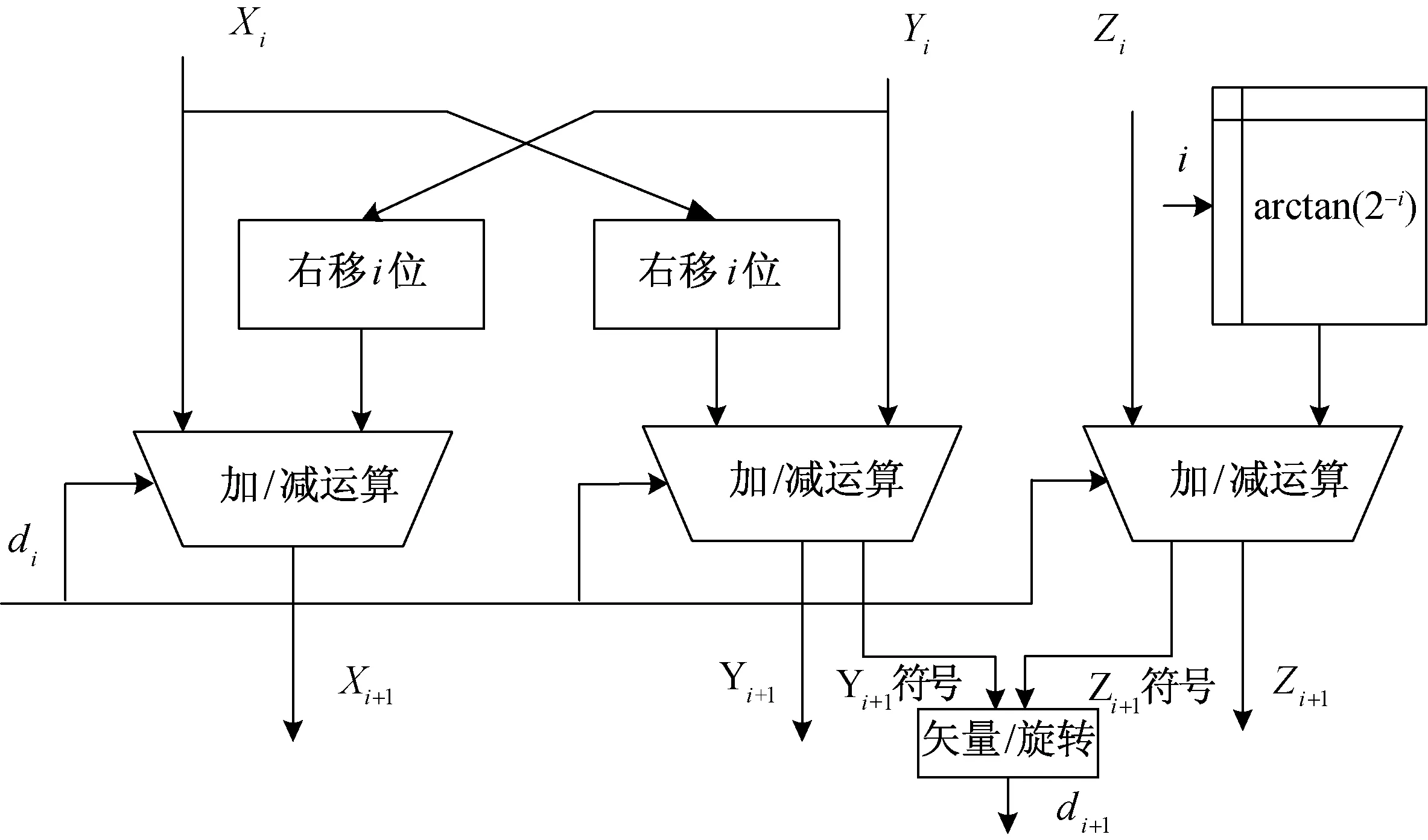
图2 CORDIC单级迭代框图

4 仿真验证

考虑0°～60°指向角度范围，以补偿前频率为15.15 GHz、补偿后频率为14.80 GHz、角度步进为0.01°为例，通过CORDIC算法计算频率补偿后的指向角度的仿真结果如图3所示，从仿真结果可以看出当步进量为0.01°时，通过CORDIC算法能够很好的计算出频率补偿后的指向角度，该结果与理论频率补偿后的指向角度之间的相对误差仿真结果如图4所示，通过仿真结果可知通过CORDIC算法计算的频率补偿后的指向角度结果与理论频率补偿后的指向角度之间的相对误差在2%以内，将程序下载到FPGA中经过验证满足设计要求。

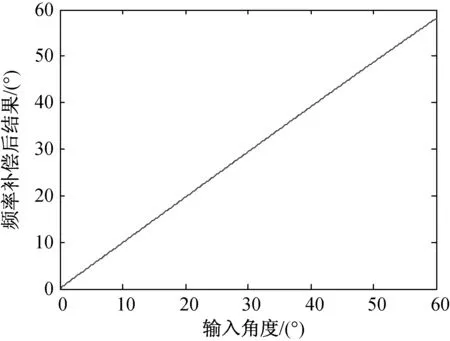
图3 CORDIC算法计算波束指向频率补偿仿真图

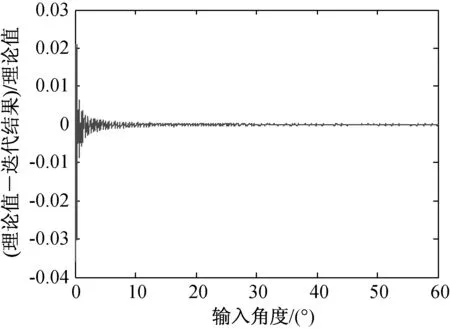
图4 CORDIC计算结果和频率补偿理论值相对误差仿真图

5 结论

相控阵天线波控机设计需要大量FPGA的ROM资源存储脱机计算数据，本文通过使用CORDIC算法替代查找表法计算频率补偿后的波束指向角度，在很大程度上节省了ROM资源，对于相控阵天线波控机设计具有重要的意义。

[1] 王梦源,王书省,陈星．流水线双模CORDIC算法的FPGA实现[J]．电子测量技术， 2007,(9)： 184-185.

[2] 周涛,崔瑞雪．基于CORDIC算法实现双曲函数的计算[J]．华北航天工业学院学报， 2006,(4)： 15-17.

[3] 张建斌,梁芳,刘乃安．一种改进型CORDIC算法的FPGA实现[J]．微电子学与计算机， 2010,(11)： 182-184．

[4] 余捷,杜栓义,何纬．基于改进型CORDIC算法数字下变频FPGA实现[J]．电子科技， 2008,(2)： 63-66．

[5] 余建宇,罗丁利,陈矛．基于CORDIC算法的数字鉴频方法及其在FPGA中的实现[J].火控雷达技术， 2007,(36)： 72-76.

ApplicationofCORDICAlgorithminBeamPointingFrequencyCompensation

ZOUXiao-dong,YIKun,XIALi-nuo,ZHUWei-cai

(Shanghai Radio Equipment Research Institute, Shanghai 200090, China)

The dynamic scanning of phased array antenna is realized by the change of phase gradient in the array, the phase gradient between the elements in the array is generated by the phase shifter. In order to achieve the same beam pointing at different frequencies, it is necessary to compensate the frequency of beam pointing, using CORDIC algorithm instead of look-up table algorithm to calculate the result of sine and cosine, it solves the problem that the look-up table algorithm takes up a large amount of resources in the range of error, the idea passed through the MATLAB simulation and FPGA design and verification.

phased array antenna; beam pointing; frequency compensation

1671-0576(2017)02-0011-04

2017-02-09

国家自然科学基金项目(项目编号：41406206);国家自然科学基金项目(项目编号：61401280)。

邹小东(1987-)，男，工程师，硕士，主要从事相控阵雷达导引头技术研究。

TJ765.331

A