某型车用发电机电磁噪声的数值仿真∗

贺岩松，张全周，赵 勤，孔祥杰

(1.重庆大学汽车工程学院，重庆 400044； 2.汽车噪声振动和安全技术国家重点实验室，重庆 401120)

某型车用发电机电磁噪声的数值仿真∗

贺岩松1，2，张全周1，赵 勤2，孔祥杰2

(1.重庆大学汽车工程学院，重庆 400044； 2.汽车噪声振动和安全技术国家重点实验室，重庆 401120)

针对某型车用爪极发电机存在的电磁噪声问题，建立了发电机的电磁学有限元模型、动力学有限元模型和声学边界元模型，进行多物理场耦合的数值仿真，获得发电机的电磁力波、振动响应和外部声场噪声等信息。对比仿真与实验分别得到的测试半球面上的平均声压级，发现两者吻合较好，说明该数值仿真方法具有较高的精度。最终结果表明，发电机后端盖无支耳一侧的36阶振动是引起电磁噪声的主要原因，为车用发电机的电磁噪声控制提供了参考。

车用发电机；电磁噪声；多物理场耦合仿真；噪声源识别

前言

汽车在中、低速行驶时的主要噪声源是发动机。但是在起步、怠速等工况下，发动机的噪声并不显著，而车用发电机会发出一种高频的电磁啸叫，这对汽车的乘坐舒适性有很大影响。因此，很有必要对发电机的电磁噪声进行研究。

电机气隙磁场中的电磁力波作用在定子齿尖上，使电机发生结构振动，进而向外辐射电磁噪声。它涉及到电磁学、振动学和声学等多个物理场。为对其进行预测，需要建立电机的电磁学模型、动力学模型和声学模型，用以计算电机气隙磁场中的电磁力波和电机的结构振动，并最终得到电机外部声场的噪声信息[1]。上述的电磁学模型、动力学模型和声学模型皆可通过解析的方法建立[2-3]，解析模型能较好地识别电机电磁力波、结构振动和外部声场噪声频率，但在预测以上物理量的幅值时精度较差。随着计算机技术的发展，有限元(FEM)和边界元(BEM)等数值仿真方法应用于电机电磁噪声的预测。数值仿真方法对电机结构的复杂性进行了充分考虑，并能对电机电磁力波、结构振动和外部声场噪声的幅值和频率进行较为准确的预测[1，4-8]。但以上研究对象多为感应电机和同步电机等传统电机，有关车用发电机(爪极电机)的研究相对较少。不同于传统的2D电机，爪极电机由于存在爪极，其结构具有明显的3D特征，在进行数值仿真时必须建立3D模型。部分学者对爪极电机的电磁场和结构振动进行了研究[9-12]，但从电磁、振动和声学角度对其电磁噪声进行系统研究的文献相对缺乏。

本文中将针对某型车用发电机(爪极电机)，建立其3D电磁学模型、动力学模型和声学模型，并在此基础上，采用多物理场(电磁、振动、声学)耦合的数值仿真方法，以3 000r/min工况为例，对其电磁噪声进行研究，并通过实验对数值仿真结果进行验证。

1 数值仿真方法介绍

为预测车用发电机的电磁噪声，须建立其电磁学模型、动力学模型和声学模型，用以计算电机气隙磁场中的电磁力波和电机的结构振动，并最终获得电机外部声场的噪声信息。发电机电磁噪声的数值仿真涉及电磁学、振动学和声学等多个物理场，且各物理场之间存在紧密的联系，因此称其为多物理场耦合仿真。

车用发电机电磁噪声多物理场耦合仿真的流程如图1所示。首先，借助电磁仿真软件Ansoft，建立发电机的3D电磁学有限元模型，以电流或电压激励作为输入对其进行电磁学仿真，求解作用在定子齿尖上的电磁力波。其次，利用Ansys软件，建立发电机的3D动力学有限元模型，并以作用在定子齿尖上的电磁力波作为激励对其进行动力学仿真，求解发电机结构的振动响应。最后，在Virtual Lab中，建立发电机的声学边界元模型，并以发电机外表面的振动位移作为边界条件对其进行声学仿真，求解发电机外部声场的噪声信息。

图1 多物理场耦合仿真流程

2 多物理场耦合仿真

2.1 电磁学仿真

电机气隙磁场中的电磁力波是引起其电磁噪声的根源，这里进行电磁学仿真的目的是求解作用在定子齿尖的电磁力波。建立发电机的电磁有限元模型，如图2所示。

图2 电磁有限元模型

采用麦克斯韦应力张量法，计算电磁力密度的径向分量Pr和切向分量Pt(轴向分量为零)：

式中：P为电磁力密度；B为气隙磁密；μ0为空气的磁导率；下标r和t分别表示径向分量和切向分量。

在定子齿尖面上，对式(1)和式(2)中得到的电磁力密度进行积分，求得作用在定子齿尖上的电磁力波。在Ansoft软件中，采用时步有限元法可得到电磁力波的时域曲线，如图3所示。但动力学仿真中需要以频域形式的电磁力波作为输入，故对上述时域数据进行FFT变换，得到电磁力波的频谱，如图4所示。

2.2 动力学仿真

动力学仿真是联系电磁学仿真与声学仿真的纽带。它以电磁学仿真中得到的电磁力波作为输入，求解电机的结构振动响应；并以此作为后续声学仿真的边界条件，以便求解电机外部声场的噪声信息。

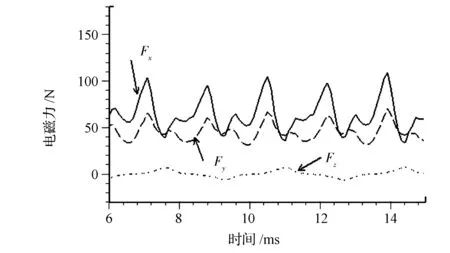
图3 电磁力波时域曲线

图4 电磁力波频谱

动力学仿真的基础方程为

式中：M，C和K分别为质量矩阵、阻尼矩阵和刚度矩阵；x为位移矢量；F为力矢量。

以作用在定子齿尖上的电磁力波作为输入，也即力矢量F为已知量，要求解电机的位移矢量x，还需知道电机的质量矩阵M、阻尼矩阵C和刚度矩阵K。电机的质量矩阵M是显而易见的；在仿真中将电机各阶模态的阻尼比设为2%，也即阻尼矩阵C为已知量；则问题的关键就在于电机刚度矩阵K的确定。电机的刚度矩阵K与电机中各部件的接触状态密切相关。车用发电机(爪极电机)与以往的电机结构有所不同，其定子被包裹在前、后端盖之间，它们之间的接触状态对电机的刚度矩阵有很大影响。此外，因定子绕组的结构相对复杂，若直接建立定子绕组的模型进行仿真，难度较大；这里将定子绕组简化成嵌放在定子槽内的分离铜块[13]，并根据仿真与模态实验结果不断调整更新简化后定子绕组的杨氏模量，直至仿真与实验结果相吻合。最终建立的发电机动力学有限元模型如图5所示。

在Ansys软件的谐响应分析模块中，将电磁力波加载到上述动力学有限元模型上，并利用模态叠加法计算发电机的动力学响应。图6为发电机在36阶频率下的位移变形图，可以看出，后端盖无支耳一侧的振动变形尤为显著。

图5 动力学有限元模型

图6 36阶频率下的位移变形图

2.3 声学仿真

电机的电磁噪声是电磁力波使电机发生结构振动，进而向外辐射噪声引起的。在算得发电机在电磁力波作用下的动力学响应的基础上，可采用间接边界元法求解发电机外部声场的噪声信息。

首先，抽取动力学有限元模型的表面网格，建立发电机边界元模型，如图7所示。同时，为模拟发电机噪声测试的实验环境(如图8所示)，在发电机模型的下方设置了隔音板，并在其上方布置了半球测试面，如图9所示。

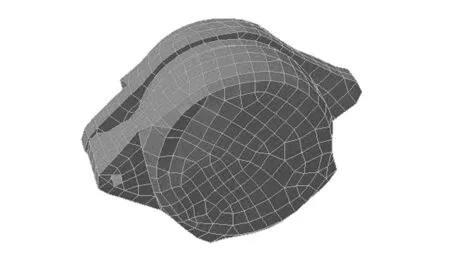
图7 声学边界元模型

图8 发电机噪声测试环境

图9 发电机的声学仿真环境

以发电机外表面质点的振动位移作为边界条件，质点振动位移s与振动速度v之间的关系为

发电机外表面质点振速的法向分量vn为已知量，根据边界元法的基本原理，发电机外表面S上的声压满足如下关系[14]：

式中：H和B为与激励频率和电机的结构振型有关的矩阵；pS和vn分别为发电机外表面上的声压和质点振速的法向分量。

发电机外部声场中任意一点处的声压pf可表示为[14]

通过声学仿真可求得发电机外部声场的噪声信息。图10为测试半球面上平均声压级的仿真与实验结果对比。同时，为便于后续分析，这里还提取了36阶频率下的发电机外部声场云图，如图11所示。

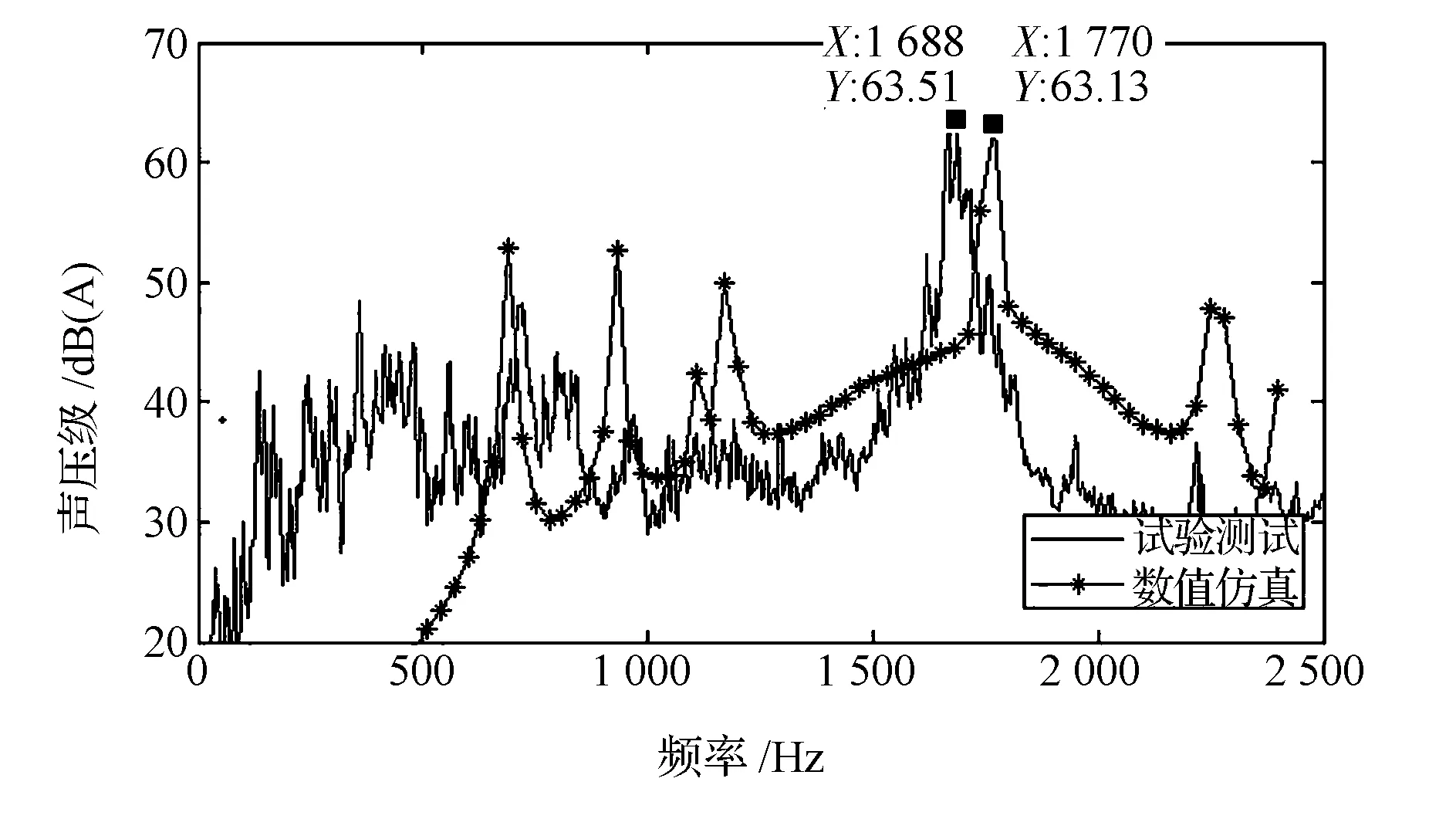
图10 测试半球面上平均声压级的仿真与实验结果对比

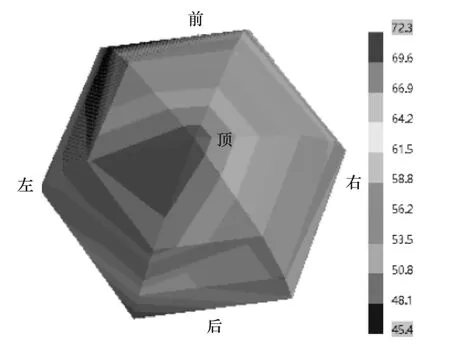
图11 36阶频率下的发电机外部声场云图

3 仿真与实验结果分析

为明确发电机电磁噪声的产生机理，对以上数值仿真的结果做简要分析。

图10为测试半球面上平均声压级的仿真与实验结果对比。由图可见：两者都在36阶频率处出现了最高峰值，且该处峰值比其它峰值高出10dB以上，也就是说该处峰值可表征测试半球面上的平均声压级；对比发现，仿真与实验得到的36阶频率下的声压级相差在0.5dB以内，这说明该数值仿真方法具有较高的精度。

测试半球面上平均声压级的最大峰值之所以出现在36阶频率处，最根本的原因在于激发电磁噪声的电磁力波。前面提到的36阶频率是从电磁噪声的角度来划分阶次的，其频率f1和阶次O1之间的关系为f1＝(n/60)×O1。 从电磁力波的角度来划分阶次时，其频率f2和阶次 O2之间的关系为 f2＝(np/60)×O2(其中p＝6，表示电机的极对数)。那么，前面提到的12，24和36阶电磁噪声的频率就与2，4和6阶电磁力波的频率相对应。这里引入一个电角度的概念，电角度α与机械角度β之间的关系为α＝pβ。该发电机定子相邻齿之间存在机械角度差 θ1＝ 360°/Z ＝ 10°(其中 Z＝36，为电机的定子齿数)。因此，发电机定子相邻齿之间的电角度差θ2＝pθ1＝60°，即其各阶电磁力波在相邻定子齿之间存在φ＝60°×O2的相位差。而2，4和6阶电磁力波在定子相邻齿之间分别存在120°，240°和360°的相位差，也即各个定子齿上的6阶电磁力波始终是同相位的，这就是36阶电磁噪声最为显著的原因。

为进一步明确该型发电机电磁噪声的来源，提取了36阶频率下的发电机外部声场云图，如图11所示。由图可见，发电机后方的噪声最为显著，分析认为可能是发电机后端盖等结构的振动引起的。为此，提取发电机在36阶频率下的位移变形图，由图6可见，发电机后端盖无支耳的一侧产生了较大的振动变形，这正是发电机后方噪声的主要来源。

基于以上分析，36阶频率下后端盖无支耳一侧的振动是该型发电机电磁噪声的主要来源，是其电磁噪声控制的重点，可以通过增加该位置刚度(如添加支耳)，以减小该处的振动变形，从而降低了发电机后方的电磁噪声。

4 结论

本文中采用多物理场耦合的数值仿真方法对某型车用发电机在3 000r/min的电磁噪声进行了研究。通过建立发电机的电磁学有限元模型、动力学有限元模型及声学边界元模型，进行耦合仿真，计算了发电机的电磁力波、振动响应和外部声场噪声信息，得出了如下结论。

(1)测试半球面上平均声压级的最大峰值出现在36阶频率处，且该处峰值比其它峰值高出10dB以上，这是由于该频率所对应的6阶电磁力波在各个定子齿上始终是同相位的。

(2)仿真与实验得到的36阶频率下的声压级相差在0.5dB以内，说明该数值仿真方法具有较高的精度。

(3)提取36阶频率下的发电机外部声场云图，发现发电机后方的噪声最为显著；观察发电机在36阶频率下的位移变形图，发现发电机后端盖无支耳一侧发生了较大的振动，这说明发电机后方噪声主要是由后端盖无支耳一侧的振动引起的；对此，可通过增加该位置刚度，对电机的电磁噪声进行控制。

[1] DOS Santos F L M， ANTHONIS J， NACLERIO F， et al.Multiphysics NVH modeling：simulation of a switched reluctancemotor for an electric vehicle[J].IEEE Transactions on Industrial Electronics，2014，61(1)：469-476.

[2] TIMÁR-P L T P， TÍMÁR P L.Noise and vibration of electrical machines[M].North Holland，1989.

[3] CHO D H，KIM K J.Modelling of electromagnetic excitation forces of small induction motor for vibration and noise analysis[J].IEEE Proceedings-Electric Power Applications，1998，145(3)：199-205.[4] NEVESC G C，CARLSON R，SADOWSKIN，et al.Calculation of electromagnetic-mechanic-acoustic behavior of a switched reluctancemotor[J].IEEE Transactions on Magnetics，2000，36(4)：1364-1367.

[5] GIERAS JF，WANG C，LAIJC.Noise of polyphase electricmotors[M].CRC Press，2005.

[6] DUPONT JB，BOUVET P.Multiphysicsmodelling to simulate the noise of an automotive electric motor[C].SAE Paper 2012-01-1520.

[7] BRUDNY J F， SZKUDLAPSKI T，MORGANTI F， et al.Method for controlling the pwm switching：Application to magnetic noise reduction[J].IEEE Transactions on Industrial Electronics，2015，1(62)：122-131.

[8] 代颖，崔淑梅，张千帆，等.车用异步电机的电磁振动/噪声分析[J].中国电机工程学报，2012，32(33)：89-97.

[9] RAMESOHL I， HENNEBERGER G， KUPPERS S， et al.Three dimensional calculation ofmagnetic forces and displacements of a claw-pole generator[J].IEEE Transactions on Magnetics，1996，32(3)：1685-1688.

[10] YANG F，BAO X，DIC，etal.Study of reducing electromagnetic vibration by claw-pole brazing for automobile claw-pole alternators[C].Electrical Machines and Systems(ICEMS)，2015 18th International Conference on IEEE，2015：184-188.

[11] CONSTANTIN S， DUMITRU C， LEONARD M.3D numerical modeling with FEM operation under load on the alternator claw poles[C].Electronics，Computers and Artificial Intelligence(ECAI)，2015 7th International Conference on IEEE，2015：75-80.

[12] 鲍晓华，刘健，倪有源，等.汽车爪极发电机定子模态分析和固有频率计算[J].汽车工程，2011，33(12)：1088-1091.

[13] NODA S， MORIS， ISHIBASHIF， et al.Effect of coils on natural frequencies of stator cores in small inductionmotors[J].IEEE transactions on energy conversion，1987(1)：93-99.

[14] FURLAN M，CERNIGOJA，BOLTEZAR M.A coupled electromagnetic-mechanical-acoustic model of a DC electric motor[J].COMPEL-The International Journal for Computation and Mathematics in Electrical and Electronic Engineering，2003，22(4)：1155-1165.

Numerical Simulation on the Electromagnetic Noise of a Vehicle Alternator

He Yansong1，2， Zhang Quanzhou1， Zhao Qin2＆ Kong Xiangjie2
1.School of Automotive Engineering， Chongqing University， Chongqing 400044；
2.State Key Laboratory of Vehicle NVH and Safety Technology，Chongqing 401120

Aiming at the existing electromagnetic noise issue of a vehicle claw-pole alternator，the electromagnetic finite element(FE)model，dynamics FEmodel and the acoustic boundary elementmodel of alternator are built to conduct a multi-physical-field coupling numerical simulation，with the information on the electromagnetic force wave，vibration response and exterior acoustic noise field of alternator obtained.The comparison on the average sound pressure level on the testing semi-spherical surface obtained from simulation and experiment show that both results agree wellwith each other，demonstrating the high accuracy of the numerical simulation scheme adopted.The final results indicate that themain source of the electromagnetic noise of alternator is the 36th order vibration of the side without lug of its rear-end cover，providing references for the electromagnetic noise control of vehicle alternator.

vehicle alternator； electrom agnetic noise； m ulti-physical-field coup ling simulation； noise source identification

10.19562/j.chinasae.qcgc.2017.10.016

∗国家自然科学基金(51275540)和汽车噪声振动和安全技术国家重点实验室项目(Q145615)资助。

原稿收到日期为2016年9月12日，修改稿收到日期为2016年11月16日。

贺岩松，教授，博士生导师，E-mail：hys＠ cme.cqu.edu.cn。