悟透导数本质 探析物理变化率问题

(湖北省武汉市黄陂区教学研究室，湖北 武汉 430300)

悟透导数本质探析物理变化率问题

唐克明

(湖北省武汉市黄陂区教学研究室，湖北 武汉 430300)

通过高中数学导数知识的学习，强化了学生的数学能力，丰富了物理问题解决的途径。本文阐释了导数本质、几何意义、物理意义，并应用求导的数学工具，简单明了、形象直观地探讨一些物理现象和实例，总结物理学中变化率问题的处理思路，这有益于高三复习中的数理学科综合，有益于培养学生应用数学知识解决物理问题的能力。

导数；变化率；数学知识；物理问题

1 引言

导数的知识已纳入高中数学教材，在数学高考中已作为必考内容，这是新课改的一大亮点，为高中生解决物理问题增添了有力的数学工具。鉴于这部分知识是在高二下学期学完，那么在高三的一轮复习中，可以有意识地指导学生利用导数知识重新认识物理概念，同时培养学生应用导数分析物理问题的能力。

2 导数知识的回顾

17世纪力学、航海、天文等方面取得了突飞猛进的发展，这些发展对数学提出了新的要求，其中“根据物体的路程关于时间的函数求速度和加速度、求已知曲线的切线”这两类问题直接导致了导数的产生。

2.1 导数的定义

2.2 导数的本质与几何意义

由导数的定义可知“导数表示函数在某一点处由于自变量变化所引起的函数变化的快慢程度，即表示函数变化的变化率，但在数学上一般都称为导数”，我们可以认为导数的本质就是函数的变化率。

图1

2.3 导数的物理意义

关于导数的物理意义没有一个统一的说法，对于不同的物理问题有不同的意义，凡是在物理问题中，涉及物理量的变化率的问题，一般都是利用导数来解决。

在导体中，通过横截面的电量Q是时间t的函数，即Q(t)，则Q(t)对时间t的导数，就是电流强度I(t)=Q′(t)，即是电量对时间的变化率。

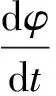
3 问题例析

3.1 探讨“气球膨胀率”

生活中很多人都看到过这样一个物理现象：在给气球打气的过程中，发现随着气球内空气容量的增加，气球的半径增加得越来越慢。这一现象称之为“气球膨胀率”,即半径随容积变化的快慢，从物理学的角度可以定性分析，但要定量描述这一现象，还需要借助数学工具来探讨。若对这一物理现象作如下的导数分析，能启迪学生的思维，有益于学生“应用数学知识解决物理问题能力”的培养，分析如下。

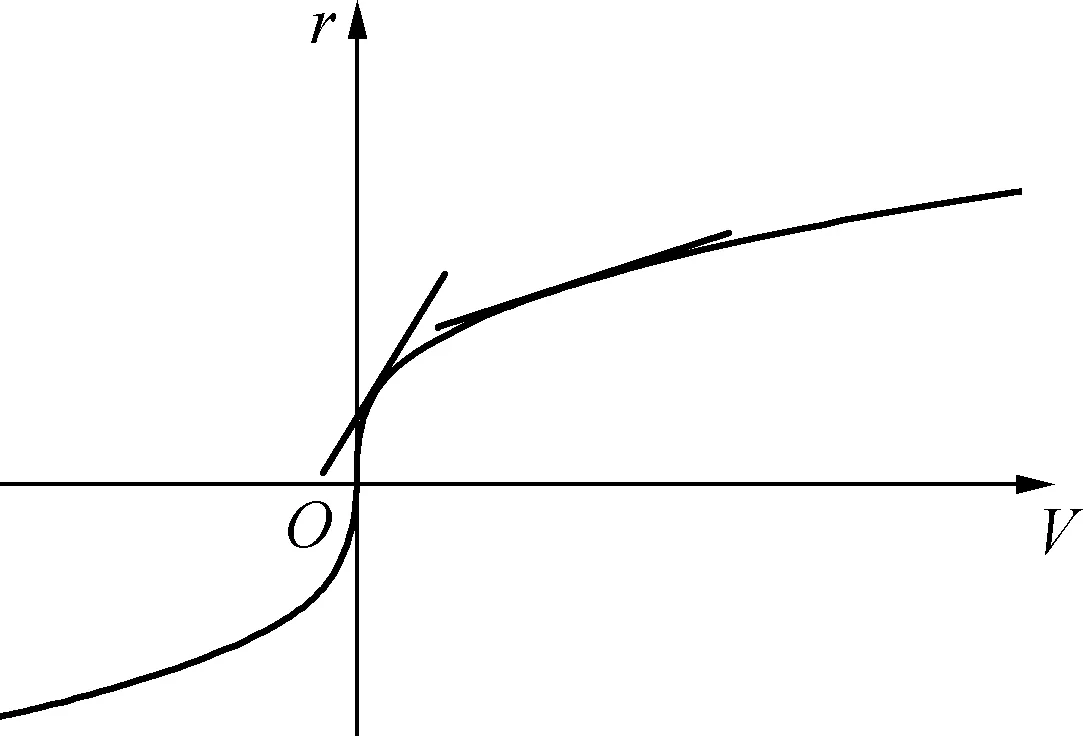
图2

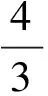
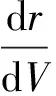
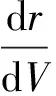
3.2 探讨“万有引力随物体离地高度h增大，减少得越来越慢”

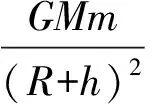
图3

图4

3.3 探讨“高台跳水，速度的变化”

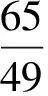
3.4 探讨“简谐运动，速度随位移的变化快慢”

图5

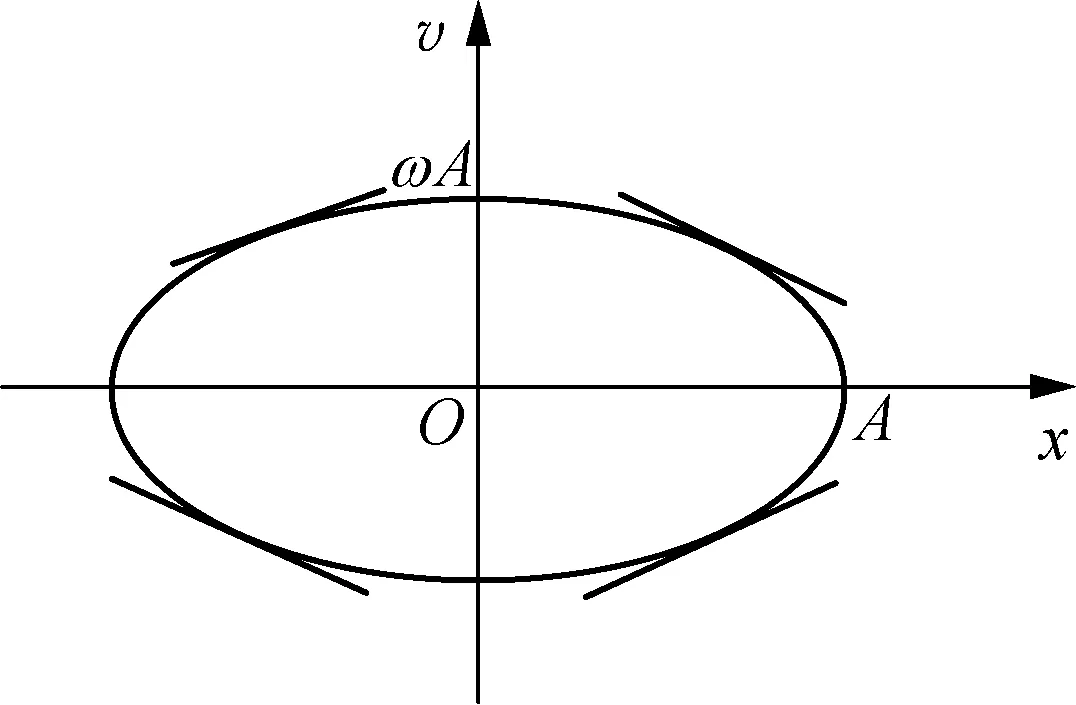
图6

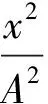
拓展探究：振子m的动能Ek，随时间t的变化快慢；随位移x的变化快慢。

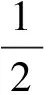
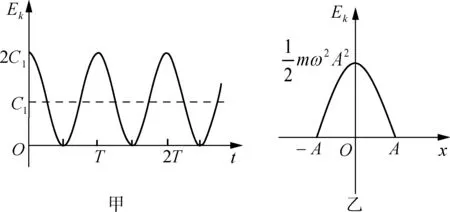
图7

4 小结

在物理学中，要探讨物理量的变化率问题，可用物理规律建立两者间的函数关系，用计算机作出它们的函数图像，用导数的几何意义或原函数一阶导数的单调性来判断解决，这是我们解决物理学中关于变化率问题的思路。

[1] 苏文芳.力学[M].武汉：华中师范大学出版社，1992：6-7.

[2] 俞礼钧,王裕民.应用高等数学(上册)[M].武汉：华中科技大学出版社，2006:44，47-48.

[3] 宋正怀,刘红琴.图像斜率物理意义的教学探讨[J].物理之友,2015,(6).

[4] 陈玉奇.用导数巧解一道竞赛压轴题[J].物理之友,2014,(10).