对人教版物理选修3-3一道习题解答的商榷

(安徽省临泉第一中学,安徽 临泉 236400)

·试题研究·

对人教版物理选修3-3一道习题解答的商榷

郭雪鹏

(安徽省临泉第一中学,安徽 临泉 236400)

在教学中发现,学生对人教版物理3-3教师用书中一道习题的解答存在质疑，笔者对此进行了分析,并提供了另外两种解答。

托里拆利实验;教材习题;教学用书

1 问题的提出

图1

在人教版物理选修3-3“理想气体的状态方程”一节后有这样一道习题:在做托里拆利实验时,玻璃管内有些残存的气体,此时玻璃管竖直放置,如图1所示，假如把玻璃管竖直向上提起一段距离,玻璃管下端仍浸在水银中,则管内空气体积如何变化？管内水银柱长度如何变化？管内空气压强如何变化?

教师用书给的参考解答如下:由于外界大气压不变,玻璃管内空气含量较少,对压强影响不是很大。因此,当玻璃管竖直向上提起时,管内水银柱的高度变化不会很大,管内空气柱长度增加,体积增大。我们可以把这个过程看做等温过程,由于体积增大,玻璃管内空气压强会减小,水银柱的长度会增加。也可以利用理想气体状态方程,可定量计算玻璃管内空气柱的体积和压强的变化情况。

2 对教师用书参考解答的质疑

在教学中学生对这个参考解答存在质疑,认为教师用书给出的解答自相矛盾，学生提出的问题如下。

问题1:认为玻璃管内空气含量较少,对压强影响不是很大,也就是忽略了管内空气压强的影响,向上提起,认为水银柱的高度变化不会很大。而在后面又得出了压强会减小,水银柱长度会增加的结论。前面的假设和后面得出的结论自相矛盾。

问题2:如果玻璃管上方不是残存少量气体,而是上方有一段空气柱。把玻璃管竖直向上提起,教师用书给出的解答将不适用。

笔者也认为教师用书给出的解答的确存在问题,前后的说法不一致,逻辑推理不严密,缺乏足够的说服力。对于问题2,认为玻璃管内上方有一段空气柱,此时管内空气压强的影响将不得不考虑,因此教师用书的参考解答无法解决此问题。笔者经过思考,提供另外两种解答方法,叙述如下。

3 笔者的解法

3.1 公式推导

如图2所示，设玻璃管横截面积为S,玻璃管内水银柱高度为h1,玻璃管内空气柱长度为l1,压强为p1。将玻璃管竖直向上提起一段距离后,玻璃管内水银柱的长度变为h2,玻璃管内空气柱的长度变为l2,压强变为p2。

图2

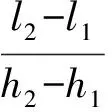
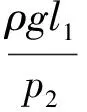
3.2 反证法

假设管内空气体积减小(或不变),玻璃管横截面积不变,空气柱的长度将减小(或不变),将管内空气变化视为等温变化,玻璃管空气的压强将增大或(不变),由于将玻璃管竖直向上提起一段距离,玻璃管内水银柱长度将增加,水银柱产生的压强增大。这样导致管内空气压强与水银柱产生的压强之和将大于外界大气压强,无法保持平衡,假设错误,因此管内空气体积将增大,管内空气压强减小。由于管内空气压强与水银柱压强之和等于外界大气压强,因此水银柱产生的压强增大,管内水银柱长度增加。

4 结语

笔者用两种方法解决了学生的疑惑，第一种解法是通过公式推导,运用玻意耳定律,通过数学推理,对学生的数理推导能力要求较高;第二种解法是应用反证法得到结论，学生对反证法较陌生,这也正是学生在学习热学中需要加强的。

[1]人民教育出版社,课程教材研究所，物理课程教材研究开发中心.普通高中课程标准教科书 物理选修3-3[M].北京:人民教育出版社,2010:25.

[2]人民教育出版社,课程教材研究所，物理课程教材研究开发中心.普通高中课程标准教科书 物理选修3-3教师教学用书[M].北京:人民教育出版社,2008:45.