琼州海峡海口站近岸风暴增水概率风险分析

陈玲舫，韩树宗，车志伟，罗 耀，谢 强

(1. 中国科学院 深海科学与工程研究所，海南 三亚 572000； 2. 中国海洋大学 海洋与大气学院，山东 青岛 266100； 3. 国家海洋局 海口海洋环境监测中心站，海南 海口 570100； 4. 中国科学院 南海海洋研究所，广东 广州 510301)

琼州海峡海口站近岸风暴增水概率风险分析

陈玲舫1，韩树宗2，车志伟3，罗 耀4，谢 强1

(1. 中国科学院 深海科学与工程研究所，海南 三亚 572000； 2. 中国海洋大学 海洋与大气学院，山东 青岛 266100； 3. 国家海洋局 海口海洋环境监测中心站，海南 海口 570100； 4. 中国科学院 南海海洋研究所，广东 广州 510301)

基于海口站1976～1997年逐时潮位和逐日最大风速资料，利用阿基米德Copula函数构建海口年最大增水与相应日期最大风速的联合概率分布模型。结果表明：1)广义极值分布可作为海口站年最大增水和相应日期最大风速的边缘分布。两个序列之间存在强正相关关系，G-H Copula函数更适用于作为海口站年最大增水和相应日期的最大风速联合概率分布的连接函数。2)两变量联合作用的同频率增水高度设计值与增水的单变量边缘分布设计值之间的相对差值约为7.5%。3)条件概率1(P(Y≥y|X≥x))中同频率的年最大增水和相应风速的遭遇概率介于78.2%～80.9%，条件概率2(P(Y≥y|X≤x))中同频率的年最大增水和相应风速两者的遭遇概率小于4.8%。

琼州海峡；Copula函数；联合分布；风暴增水；遭遇概率

Abstract: Based on the hourly tidal level and daily maximum wind speed data at Haikou Station during 1976～1997, the joint probability distribution of yearly maximum surge height and corresponding wind speed has been analyzed with the Archimedean Copula functions. The main conclusions are as follows: 1) Generalized extreme value distribution can be used as the optimal margin distribution for yearly maximum surge height and corresponding wind speed at Haikou station. There is a strong positive correlation between the two variables. Among the three Archimedean Copula functions, G-H Copula is a better contiguous function for joint distribution of the two variables. 2) By comparing the joint distribution, the relative differences of the design values of the marginal distribution of surge heights are about 7.5%. 3) Conditional probability 1 (P(Y≥y│X≥x))indicated that the encounter probabilities of the same frequency of yearly maximum surge heights and corresponding wind speeds fall in between 78.2%～80.9%, and the conditional probability 2(P(Y≥y│X≤x)) indicated that the encounter probabilities of the same frequency of yearly maximum surge heights and corresponding wind speeds are less than 4.8%.

Keywords: Qiongzhou Strait; Copula function; joint distribution; storm surge; encounter probability

近半个世纪以来，气候变化造成全球各类极端天气事件频发[1]。在全球变暖背景下，南海区域台风活动加剧，登陆或者临近海南岛的台风数量也明显增多[2-3]。1953～2009年的历史资料统计表明海南岛共出现1.5 m以上的增水12次，风暴增水的频度和强度最显著区域位于海南岛的北部和东部[4]。2014年1409号台风和1415号台风引起的风暴潮过程均造成了海口超过2 m的增水。根据海口秀英潮位站的记录显示，1415号台风“海鸥”引发的风暴潮是海南岛66年来最严重的一次。台风期间，由于风暴增水叠加天文潮高潮，导致海口秀英潮位站最高潮位高达4.52 m，海口市区大部分区域被海水淹没，风暴潮叠加近岸浪，造成海口沿海护堤尽数被毁[5]，给沿岸居民的生活和生产造成了严重的威胁。因此，风暴潮增水的极值概率分布及风险研究，对海口海堤工程防灾减灾有重要的应用价值。

梁海燕等人利用Gumbel分布计算得到海口湾1 000 a一遇的极值高水位为546 cm，1 000 a一遇的风暴潮与最高天文潮的组合高水位为634 cm[6]。但其在研究中，仅考虑水位一个要素，忽略了与水位具有一定相关性的其它工程设计影响要素。随着海岸工程设计标准研究的不断推进，多元联合概率分布得到越来越多的重视，为海岸工程设计提供了更为合理的理论依据。李淑君等人利用Gumbel Ⅱ构建北部湾乌雷站台风浪和风暴增水的联合概率分布，得到了不同重现期的台风浪极值和风暴增水极值组合出现的联合概率及对应的重现期[7]。董胜等人通过不同海域的两个站点数据构建二维泊松冈贝尔逻辑分布模式，探讨了异地海域年极值风暴增水的同现规律，结果表明，两个海域同时发生稀遇潮灾的可能性较小，在防灾工程的建设中可以分别规划[8]。董胜根据龙口港25年的风暴潮增水和天文潮资料，构建二维对数正态分布函数，其确定的极端水位比规范规定的单一因素设计法降低5.2%[9]。但需要指出的是，上述二维联合概率分布对于边缘分布的选择上，具有一定的局限性。而Copula在边缘分布的选择上更加灵活[10]，已逐渐成为构建多元联合概率分布的一种重要方法，被广泛应用于海洋领域。陈子燊等人以粤东汕头海域妈屿历年最高增水高度与相应风速的遭遇为研究实例构建Copula函数，结果表明，重现期介于2～200 a之间的增水边缘分布设计值与同频率设计值的相对差值大约介于6.7%～22.2%之间[11]。王灶平等人利用Copula构建风、潮联合概率分布，发现风潮相关情况下的超越累积概率比风潮相互独立情况下高，工程中需考虑其联合概率[12]。

因此本文根据海口站的年最大增水和相应日期的最大风速数据，通过Copula 函数构建联合分布模型，分析两者之间的联合重现期、同现重现期及相应的设计值差异，并分析不同风速与不同增水之间的组合遭遇概率，为海口海岸工程设计提供更准确的参考依据。

1 研究区域及数据

海口位于海南岛北部，北临琼州海峡，海岸线长131 km，是海南省沿岸海岸带中受到海洋灾害影响最大的地区之一。海口站110°17′E，20°01′N，其附近海域地形如图1所示。

图1 琼州海峡地形分布及海口站位置Fig. 1 Topography of Qiongzhou Strait and the location of Haikou Station

琼州海峡位于雷州半岛和海南岛之间，东侧为南海北部陆架，西侧为北部湾[13]。采用全球海洋潮汐同化数据[14]，绘制琼州海峡及附近海区全日分潮[(O1+K1)/2]和半日分潮(M2)的同潮时线(实线)和等振幅线(虚线)分布，如图2所示。全日分潮振幅从琼州海峡西侧向东侧不断递减，具体而言琼州海峡西侧振幅约为0.7 m，东侧振幅约为0.2 m。由同潮时线可知，全日分潮波可通过南海北部和北部湾传进琼州海峡。半日分潮振幅则从琼州海峡西侧向东侧不断递增，琼州海峡西侧振幅约为0.2 m，东侧振幅约为0.4 m。半日潮波从北部湾进入琼州海峡，并向南海北部传播。以上结果与Shi等类似[15]。进一步计算琼州海峡海区的潮型系数，根据潮型系数的判定标准可知该海区为不规则全日潮[16-17]。

图2 日分潮[(O1+K1)/2]和半日分潮(M2)的同潮时线(实线)和等振幅线(虚线)分布。 单位：振幅(m)，相位(°)Fig. 2 Co-phase lag lines(solid lines) and Co-amplitude(dashed lines) lines of diurnal [(O1+K1)/2] and semidiurnal M2 tidal constituents. Units: coamplitude (m) and cophase (°)

采用UHSLC(夏威夷大学海平面中心)1976年1月1日～1997年12月31日的海口站逐时潮位数据，并对逐时潮位进行调和分析，利用实际水位序列减去天文潮水位序列，分离出增水序列。使用年最大值抽样法，挑选出每年增水的最大值作为年最大增水序列。而风速数据来源于国家气象局海口站的逐日风速数据，选取每年最大增水所对应日期的最大风速，作为年最大增水相应日期的最大风速序列。

通过观察年最大增水序列和相应日期的最大风速序列可发现，年最大增水序列的最大值出现在1980年，为1.96 m。其对应的风速为19.3 m/s，是相应日期的最大风速序列中的第三大值。通过对两个序列数据分析可知，年最大增水序列的偏态系数为1.77，相应日期最大风速序列的偏态系数为0.31，两者均为正偏分布。

2 方法介绍

2.1边缘分布

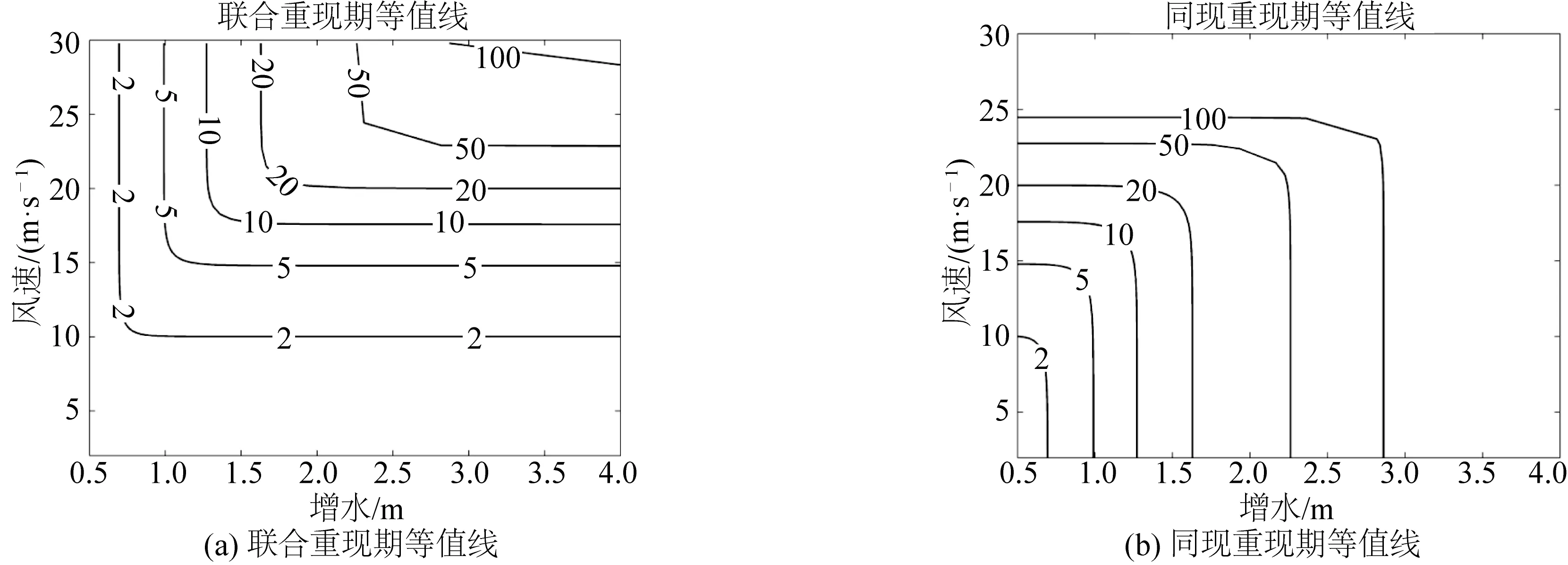
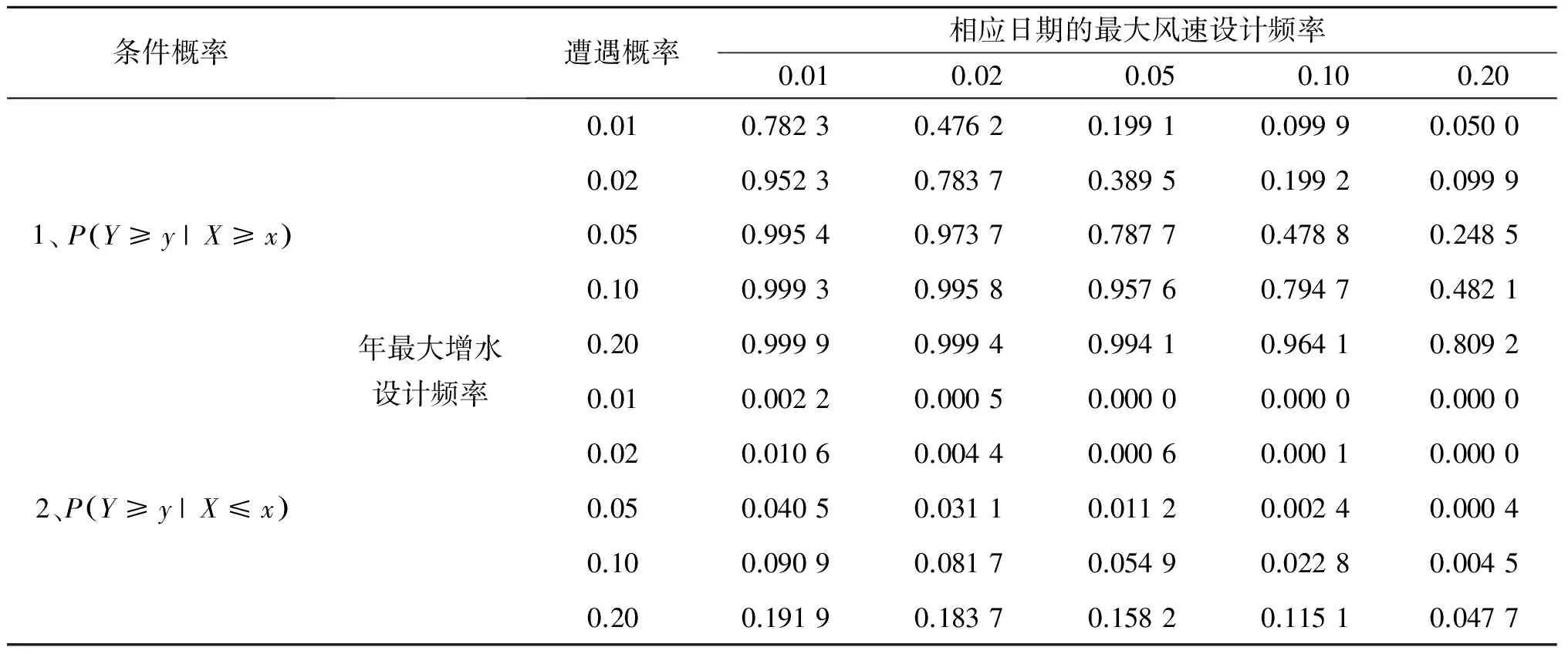
采用三参数Weibull 分布、P-III 分布[18]和GEV 分布[19]作为备选边缘分布。其概率分布函数如表1所示。同时，参数估计方法采用更适合小样本事件且对序列特大值更为稳健的线性矩法[20]或概率权重矩法[21]。拟合优度检验采用概率点据相关系数检验(PPCC)[22]、柯尔莫可洛夫-斯米洛夫检验[23]和均方根误差检验(RMSE)。在柯尔莫可洛夫-斯米洛夫检验中，本文取信度α=0.05，临界值为D0=0.178 6。若Dn

表1 三种分布函数的概率分布函数Tab. 1 Probability distribution functions for the three selected distribution functions

2.2联合概率分布

根据Sklar定理[24]，若F(x,y)为随机变量(X,Y)的二元联合分布函数，边缘分布函数分别为F1(x)、F2(y)，则存在一个Copula函数C满足

若F1(x)，F2(y)为连续分布函数，则C唯一确定；若C为一个Copula函数，则F(x,y)是一个二元联合分布函数，其边缘分布为F1(x),F2(y)。

Copula函数有很多形式，如正态Copula函数、t-Copula函数、阿基米德Copula函数族等。阿基米德Copula函数族构造方式简易且代表性广，应用于海洋、气象等多个领域。本文采用的是阿基米德Copula函数族中三种常用的二元Copula函数，包括GH-Copula函数、Clayton Copula函数和Frank Copula函数。其Copula函数表达式和Kendall秩相关系数τ与参数θ的关系式具体见文献[11, 25]。

2.3重现期计算及条件概率[26][27]

根据单变量概率分布，可以得到两变量X和Y边缘分布重现期的公式为：

对于两变量的联合分布来说，联合重现期To(x,y)指的是两个变量中一个变量发生所对应的重现期。同现重现期Ta(x,y)指的是两个变量同时发生所对应的重现期。具体计算公式见文献[11]。结合工程安全和风险管理的需要，本文主要关注以下两种条件概率：

3 分析与讨论

3.1边缘分布选取

利用Weibull 分布、GEV 分布、P-III 分布与海口站1976～1997年的年最大增水和相应日期最大风速的经验点距进行拟合，海口站年最大增水和相应日期的最大风速三种分布的拟合优度检验结果如表2所示。

表2海口站年最大增水和相应日期最大风速的边缘分布参数与拟合优度检验值

Tab.2MarginaldistributionparametersandThegoodnessoffittestvaluesfortheyearlymaximumsurgeheightandcorrespondingmaximumwindspeedatHaikoustation

样本分布PPCCDnRMSE位置参数形状参数尺度参数增水P-Ⅲ0．97370．07040．07590．46820．73392．0975Weibull0．97590．07510．07090．43760．94020．3699GEV0．99440．06380．07620．62200．31430．1917风速P-Ⅲ0．98830．09590．0927-8．635611．10780．5779Weibull0．98710．08690．1226-0．13011．942912．0845GEV0．98880．09580．09338．1657-0．11555．1097

表2中，增水和相应风速三种分布的Dn值均小于0.178 6，说明均通过了K-S检验。且综合对比表2中的三种拟合优度检验值可发现，对于海口站年最大增水和相应日期的最大风速来说，广义极值(GEV)分布与经验点距的拟合结果均较好。因此选用广义极值分布为边缘分布进行联合概率分析。海口站年最大增水和相应日期最大风速的边缘分布拟合如图3所示。

图3 海口站年最大增水和相应日期最大风速拟合Fig. 3 Fitting-figures of yearly maximum surge heights and corresponding maximum wind speeds in Haikou station

3.2Copula函数的选择

通过计算可知，海口站年最大增水和相应日期最大风速之间的Kendall秩相关系数τ为0.714 3，Spearman秩相关系数ρsV为0.889 3，线性相关系数r为0.725 4。说明两者之间为强正相关关系。从工程风险的角度来看，更为关注的是两者之间的上尾相关性，即增水与大风极端事件的遭遇概率。

采用相关性指标法分别对Archimedean Copula 函数族中的 GH-Copula函数、Clayton Copula函数和Frank Copula函数的参数值θ进行了估计，结果如表3所示。并通过Genest-Rivest图示方法[28]Ke-Kc关系图中经验点据和理论直线最接近45°对角线的参数估计方法直观选择Copula函数，Genest-Rivest方法检验结果如图4所示。

表3 海口站三种Copula函数的参数Tab. 3 Estimated parameters for three selected Copula functions for Haikou station

图4 Genest-Rivest方法检验结果Fig. 4 Genest-Rivest test results for the three functions

结合图4结果和工程风险需求，选取三种Copula函数中对上尾相关性刻画最好的GH-Copula函数作为海口站年最大增水及其相应日期最大风速联合概率分布的连接函数。根据GH-Copula函数和边缘分布，可以得出年最大增水及其相应日期最大风速的联合概率分布为：

F(X,Y)=C(FX(X),FY(Y))=exp(-[(-In(FX(X)3.5+(-In(FY(Y)3.5]1/3.5}

3.3两变量联合分布与重现期

根据联合概率分布得出一定重现期下海口站年最大增水及其相应日期最大风速的等值线图，如图5所示。其中左图为联合重现期等值线图，右图为同现重现期等值线图。

通过计算求得不同重现期下的边缘分布设计值。在给定边缘分布重现期的情况下，求出两变量的联合重现期及同现重现期，并计算出当To=T时两变量的设计值。结果如表4所示。

图5 联合重现期等值线和同现重现期等值线Fig. 5 Contour map of united recurrence (left)and co-occurrence recurrence (right)

Tab.4DesignvaluesfordifferentreoccurrenceperiodsofyearlymaximumsurgeheightandcorrespondingmaximumwindspeedatHaikoustation

T/a联合分布边缘分布设计值同频率(To=T)设计值联合重现期(To/a)同现重现期(Ta/a)增水/m风速/(m·s-1)增水/m风速/(m·s-1)100821282．9324．693．1525．195041642．2722．812．4423．362016251．6320．011．7520．63108131．2717．591．3618．285460．9914．801．0615．56

表4中数据显示，100年一遇和50年一遇的增水单变量设计值分别为2.93和2.27 m，同频率的联合分布设计值分别为3.15和2.44 m。总的来说，在给定重现期下，考虑两变量联合作用的同频率增水高度设计值与增水的单变量边缘分布设计值之间的相对差值约为7.5%，且随着重现期的增大，增水高度的联合重现设计值与单变量边缘分布设计值之间的绝对差值逐渐增大。边缘分布为100年一遇重现期下的联合重现期仅为82年，说明在一定重现期标准下，未考虑其它要素联合影响的边缘分布设计值是存在一定安全隐患的。在实际的工程建设中，可以把联合概率分布所求出的联合重现期和同现重现期作为实际重现期设定的区间，其分别对应的两个增水设计值或可视为海堤工程标准设计值的上下限。

3.4条件概率

按照式(4)和式(5)，本文分别计算年最大增水与相应日期最大风速的两种条件概率。条件概率1：P(Y≥y|X≥x)表示当风速超过某一设计标准的x时，与超过y的增水之间的遭遇概率。条件概率2：P(Y≥y|X≤x)表示当风速不超过作为标准的某一设计标准的x时，与超过y的增水之间的遭遇概率。计算结果如表5所示。

年最大增水和相应日期风速具有一定的相关性，其条件概率并不等同于两者完全独立情况下的概率。从表5上看，在给定风速设计频率的情况下，随着最大增水设计频率的增加，两者遭遇概率增加。大频率(低重现期)风速值遭遇小频率增水值的可能性非常小。对比两种条件概率可以发现，当风速不超过某一给定设计标准值时，年最大增水与相应日期最大风速的遭遇概率远小于当风速超过某一给定设计标准值时年最大增水与相应日期最大风速的遭遇概率。条件概率1中同频率的年最大增水和相应风速的遭遇概率介于78.2%～80.9%之间，而条件概率2中同频率的年最大增水和相应风速两者的遭遇概率均小于4.8%。

表5 海口站年最大增水和相应日期最大风速的遭遇概率Tab. 5 Encounter probability of yearly maximum surge height and corresponding maximum wind speed at Haikou station

4 结 语

利用海口站年最大增水和相应日期的最大风速数据，通过Copula函数构建联合分布模型，可以得到以下结论：

1)广义极值分布可作为海口站年最大增水和相应日期最大风速的最优边缘分布。海口站年最大增水和相应日期最大风速两个序列之间存在强正相关关系，G-H Copula函数可作为海口站年最大增水和相应日期的最大风速联合概率分布的连接函数。

2)在给定重现期标准下，考虑两变量联合作用的增水高度设计值与增水的单变量边缘分布设计值之间的相对差值约为7.5%，两者的差值随着重现期的增大而增大。

3)条件概率1中同频率的年最大增水和相应风速的遭遇概率介于78.2%～80.9%之间，而条件概率2中同频率的年最大增水和相应风速两者的遭遇概率小于4.8%。对两者的组合遭遇概率分析结果，可为工程的风险管理和工程设计安全提供更多的科学依据。

致谢：中国科学院南海海洋研究所热带海洋环境国家重点实验室王东晓研究员对本文提出了宝贵意见，特此表示感谢。

[1] IPCC. Climate change 2014:impacts, adaptation, and vulnerability[M/OL]. Cambridge: Cambridge University Press, http://www.ipcc.ch/report/ar5/wg2/, 2014-03-31.

[2] EMANUEL K A. Downscaling CMIP5 climate models shows increased tropical cyclone activity over the 21st century[C]//Proceedings of the National Academy of Sciences. 2013, 110(30): 12 219-12 224.

[3] DWYER J G, CAMARGO S J, SOBEL A H, et al. Projected twenty-first-century changes in the length of the tropical cyclone season[J]. Journal of Climate, 2015, 28(15): 6 181-6 192.

[4] 石海莹. 海南岛沿岸海洋灾害特征及防御对策[J]. 海洋开发与管理,2013,12:70-75.(SHI Haiying. Characteristic analysis of marine disasters and countermeasures along the coast of Hainan Island[J]. Ocean Development and Management, 2013, 12: 70-75. (in Chinese))

[5] 石海莹,李文欢,吕宇波,等. 海南省2014年两次特大风暴潮比较分析[J]. 海洋预报,2015, 32(4): 75-82. (SHI Haiying, LI Wenhuan, LV Yubo, et al. Comparative analysis of two severe storm surge of Hainan Province in 2014[J]. Marine Forecasts,2015, 32(4): 75-82. (in Chinese))

[6] 梁海燕,邹欣庆. 海口湾沿岸风暴潮漫滩风险计算[J]. 海洋通报,2004, 23(3): 20-26. (LIANG Haiyan,ZHOU Xinqing. Calculation of overland risk of storm surge off the Haikou Bay[J]. Marine Science Bulletin,2004, 23(3): 20-26. (in Chinese))

[7] 李淑君,沙文钰,齐义泉. 北部湾乌雷站台风浪、风暴增水数值结果的联合概率分析[J]. 海洋通报,2006, 25(4): 23-28. (LI Shujun,SHA Wenyu,QI Yiquan.Joint probability analysis of numerical simulation results of typhoon wave and storm surge of the Wulei station at the Beibu Bay[J]. Marine Science Bulletin,2006, 25(4): 23-28. (in Chinese))

[8] 董胜,梁永超,郝小丽. 异地海域年极值风暴增水同现规律的探讨[J]. 中国海洋大学学报:自然科学版,2004, 34(3): 468-474. (DONG Sheng, LIANG Yongchao, HAO Xiaoli. Coincidence probability study of annual extreme storm surges in different coastal areas[J]. Periodical of Ocean University of China,2004, 34(3): 468-474. (in Chinese))

[9] 董胜,付新钰,尹春维. 龙口港极端设计水位的组合估计[J]. 中国海洋大学学报:自然科学版,2008, 38(2): 323-326. (DONG Sheng, FU Xinyu, YIN Chunwei. Combined estimation of extreme designwater level at Longkou Port[J]. Periodical of Ocean University of China, 2008, 38(2): 323-326. (in Chinese))

[10] 陈超,王莉萍,陈正寿, 等. Copula函数在海洋工程中的应用[C]//第十六届中国海洋(岸)工程学术讨论会论文集(上册).北京:海洋出版社, 2013. (CHEN C, WANG L P, CHEN Z S, et al. The application of the Copula function in the ocean engineering[C] //The 16th China Ocean Engineering Academic Conference Proceedings(volume one). Beijing: The Ocean Press, 2013. (in Chinese))

[11] 陈子燊,刘曾美,李志强. 基于Copula函数的海岸增水高度与相应风速的遭遇概率分析[J]. 海洋学报,2012, 34(6): 11-18.(CHEN Zishen, LIU Zengmei, LI Zhiqiang. Analysis on encounter probabilities for coastal surge heights and corresponding wind velocities based on Copula functions[J]. Acta Oceanologica Sinica,2012, 34(6): 11-18. (in Chinese))

[12] 王灶平,刘桂平,龚政, 等. 考虑风、潮联合概率分布的海堤超越频率分析[J]. 水利水电科技进展, 2014, 34(6): 18-22.(WANG Zaoping, LIU Guiping, GONG Zheng, et al. Exceeding cumulative probability analysis of seawall considering the joint probability distribution of tide level and wind speed[J].Advances in Science and Technology of Water Resources,2014, 34(6): 18-22. (in Chinese))

[13] 侍茂崇,陈春华,黄方,等. 琼州海峡冬末春初潮余流场特征[J]. 海洋学报,1998, 20(1): 1-10.(SHI Maochong, CHEN Chunhua, HUANG Fang, et al. Characteristics of tidal current and residual current in the Qiongzhou Straits in Period between end of winter and beginning of spring[J]. Acta Oceanologica Sinica,1998, 20(1): 1-10. (in Chinese))

[14] EGBERT G D, EROFEEVA S Y. Efficient inverse modeling of barotropic ocean tides[J]. Journal of Atmospheric and Oceanic Technology, 2002, 19(2): 183-204.

[15] SHI M C, CHEN C S, XU Q C, et al. The role of Qiongzhou Strait in the seasonal variation of the South China Sea circulation[J]. Journal of Physical Oceanography, 2002, 32(1): 103-121.

[16] 俞慕耕. 南海潮汐特征的初步探讨[J]. 海洋学报,1984, 6(3): 293-300.(YU Mugeng. Preliminary discussion of tidal characteristics in the south china sea[J]. Acta Oceanologica Sinica,1984, 6(3): 293-300. (in Chinese))

[17] 丁文兰. 南海潮汐和潮流的分布特征[J]. 海洋与湖沼,1986, 17(6): 468-480. (DING Wenlan. Distribution of tides and tidal currents in the South China sea[J]. Oceanologia et Limnologia Sinica,1986, 17(6): 468-480. (in Chinese))

[18] 邱大洪. 工程水文学[M]. 第3版, 北京:人民交通出版社, 1999: 41-45.(QIU Dahong.Engineering hydrology [M]. Third Edition, Beijing: China Communications Press, 1999: 41-45. (in Chinese))

[19] GUMBEL EJ. Statistical theory of extreme values and some practical applications: applied mathematics series[J]. Journal of the Royal Statistical Society, 1955, 118(1): 10.2307/2342529.

[20] HOSKING J R M. L-moments: analysis and estimation of distributions using linear combinations of order statistics[J]. Journal of the Royal Statistical Society, Series B, 1990, 51(1): 105-124.

[21] GREENWOOD J A, LANDWEHR J M, MATALAS N C, et al. Probability weighted moments: definition and relation to parameters of several distributions expressible in inverse form[J]. Water Resources Research, 1979,15(5):1 049-1 054.

[22] FILLIBEN J J. The probability plot correlation coefficient test for normality[J]. Technometrics, 1975, 17(1): 111-117.

[23] WANG J, TSANG W W, MARSAGLIA G. Evaluating kolmogorov's distribution[J]. Journal of Statistical Software, 2003, 8(18):1-4.

[24] SKLAR A. Fonctions de répartition à n dimensions et leurs marges[J]. Paris: Publications de l'Institut de Statistique de l'Université de Paris. 1959, 8: 229-231.

[25] NELSEN R B. An introduction to copulas[M]. New York: Springer Verlag, 2006.

[26] WAHL T, MUDERSBACH C, JENSEN J. Assessing the hydrodynamic boundary conditions for risk analyses in coastal areas: a multivariate statistical approach based on Copula functions[J]. Natural Hazards and Earth System Sciences, 2012, 12(2): 495-510.

[27] 陈子燊, 曹深西. 基于Copula函数的波高与周期长期联合分布[J]. 海洋通报, 2012, 31(6): 630-635. (CHEN Zishen, CAO Shenxi. Long-term joint distribution of wave height and period based on Copula functions[J]. Marine Science Bulletin, 2012, 31(6): 630-635. (in Chinese))

[28] GENEST C, RIVEST L. Statistical inference procedures for bivariate Archimedean copulas[J]. Journal of American Statistical Association, 1993, 88(423): 1 034-1 043.

Probability risk analysis of the nearshore storm surge at Haikou Station in Qiongzhou Strait

CHEN Lingfang1, HAN Shuzong2, CHE Zhiwei3, LUO Yao4, XIE Qiang1

(1. Institute of Deep Sea Science and Engineering, Chinese Academy of Sciences, Sanya 572000, China; 2. College of Oceanic and Atmospheric Sciences, Ocean University of China, Qingdao 266100, China; 3. Haikou Marine Environment Monitoring Station of State Oceanic Administration, Haikou 570100, China; 4. South China Sea Institute of Oceanology, Chinese Academy of Sciences, Guangzhou 510301, China)

1005-9865(2017)02-0115-08

P751

A

10.16483/j.issn.1005-9865.2017.02.016

2016-06-16

三亚市院地科技合作资助项目(2015YD01)

陈玲舫(1990-)，女，福建仙游人，研究实习员，硕士，主要从事近岸海洋环境与极端水文气象事件风险概率研究。 E-mail：chlingf@idsse.ac.cn

谢 强。E-mail: gordonxie@idsse.ac.cn