错列不等直径双圆柱绕流特性数值研究

于定勇，李宇佳，马朝晖，李 龙

(中国海洋大学 工程学院，山东 青岛 266003 )

错列不等直径双圆柱绕流特性数值研究

于定勇，李宇佳，马朝晖，李 龙

(中国海洋大学 工程学院，山东 青岛 266003 )

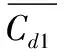
双圆柱；尾流形态；斯特鲁哈数；升力、阻力系数；错列角度

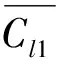
Keywords: two cylinders; wake characteristics;St;lift and drag coefficients; stagger angel

多柱(管)系统在实际工程中有着广泛的应用，如海洋平台的支柱、桥墩、海底管线、桩基式的码头等。其中，两个不同直径圆柱结构组合在一起的形式是比较常见的，比如“背负式”管线：在较大直径管体上捆绑小直径管体。水流流经这样的结构时，在其后会产生交替脱落的旋涡，交替脱落的旋涡会对上游圆柱结构产生周期性变化的作用力并激发其振动，影响结构的稳固和安全。因此对不等直径双圆柱体的绕流特性进行研究是十分必要的。

目前国内外学者主要采用物理模型实验和数值模拟两种方法研究圆柱绕流问题，研究对象主要为单圆柱和双圆柱。在实际工程中，由于水流流向的变化，错列成为两个圆柱常出现的排列形式。学者们针对错列双圆柱绕流问题已经取得了一些成果。Tsutsui[1]将物理实验和数值模拟手段相结合，利用涡方法对不等直径双圆柱在交互式流作用下的绕流现象进行了研究，采用的Re为104和4.1×104，大柱与小柱的直径分别为40和18 mm，两柱表面之间的距离为2.5 mm，θ为π/2～π，分析了θ对圆柱时均升阻力系数的影响。Zhao等[2]采用数值模拟方法对错列双圆柱绕流进行了研究，模拟选用湍流模型，Re=50 000，两柱间距与大柱直径之比G/D为0.05～0.4，小柱直径与大柱直径之比d/D为0.1～1.0，θ为0°～180°。结果表明:d/D、G/D和θ的变化均会对绕流的涡脱落频率、升阻力系数和压力系数产生影响。Zhou等[3]通过测量St数和尾流形态，研究了Re对错列双圆柱绕流的影响，间距比P/D为1.2～4.0,θ为0°～90° ,Re为1.5×103～2.0×104，将St数与Re的关系分为4种，分析发现，G/D、θ和Re均会对双圆柱绕流的St数和尾流形态产生影响。冯志鹏等[4]利用有限体积法建立了三维数值模型，研究了间距比P/D为1.2、1.6、2.0、3.0、4.0 的两交错排列弹性管在横向湍流作用下的振动响应及流场特性，通过分析发现两交错排列弹性管的运动轨迹和尾涡结构与其间距、流速密切相关。以上工作均表明在确定的Re下，θ的变化对绕流形态有明显影响，而针对θ在低亚临界Re下对不等直径双圆柱绕流涡脱落形态、St和升阻力系数的影响问题目前尚未开展相关研究。

为研究亚临界Re下错列不等直径双圆柱的绕流特性，本文基于Fluent软件中二维RNG湍流模型建立计算区域，模拟了不等直径错列双圆柱体的绕流过程，研究了Re为3 900时θ的变化对d/D为0.5、G/D为2.0的双圆柱绕流涡脱落形态和平均升阻力系数的影响。

1 数学模型

1.1控制方程

假设流体为粘性不可压缩流，因此密度不变。又假设温度变化不大，因此能量方程可以忽略。故N-S方程只考虑连续方程和动量方程。

连续方程：

动量方程：

1.2湍流模型

湍流动能方程：

湍流耗散率方程：

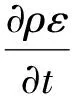
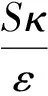
2 模型设置

2.1计算参数

文中间距比G/D=2.0，直径比d/D=0.5，θ=0°、30°、45°、60°、90°、120°、135°、150°、180°，大圆柱直径D=0.01 m，水流速度U=0.39 m/s，两圆柱表面距离为G。计算区域和圆柱布置如图1所示，两圆柱相对位置如图2所示。

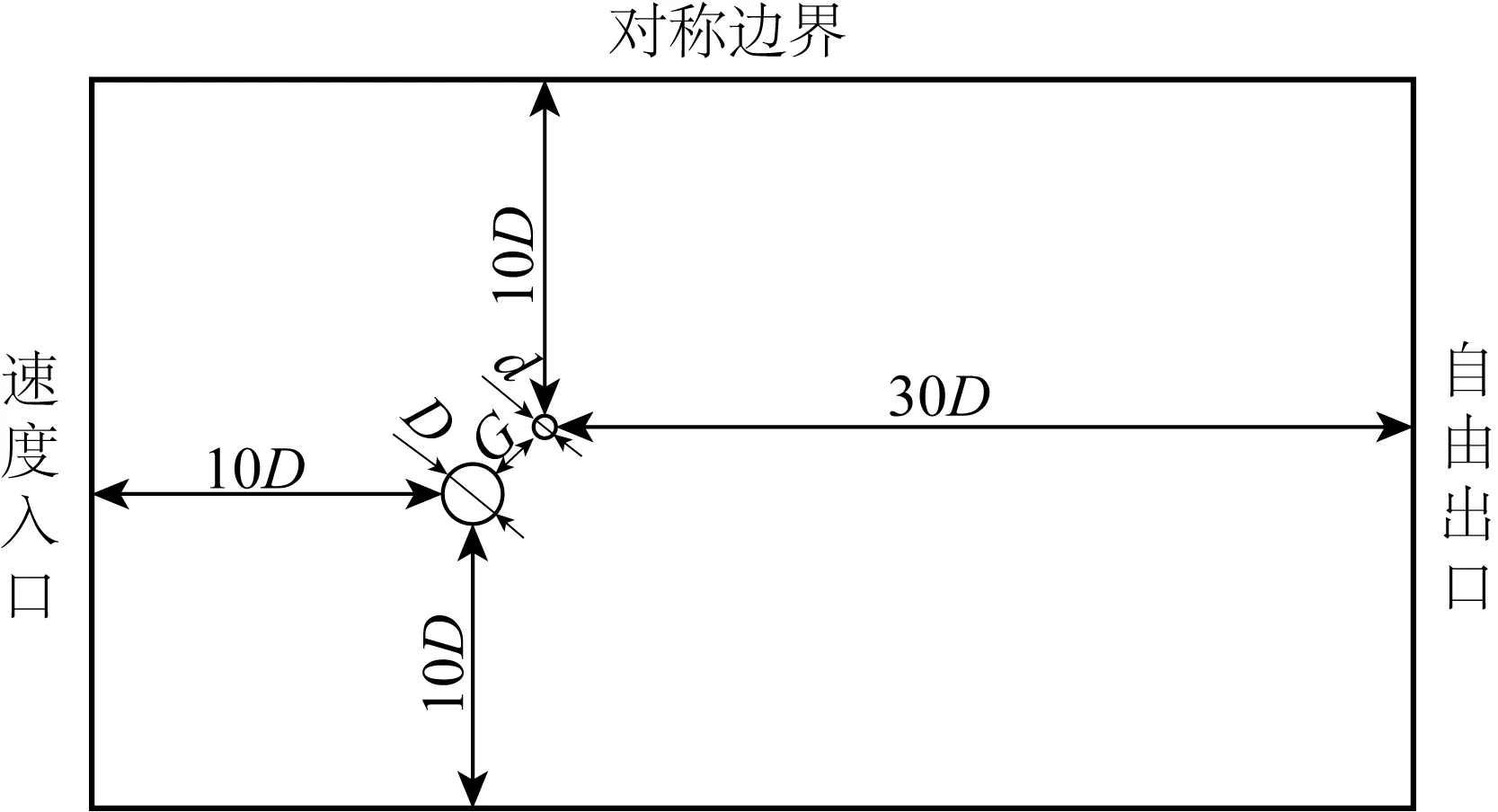
图1 计算区域Fig. 1 Computational domain

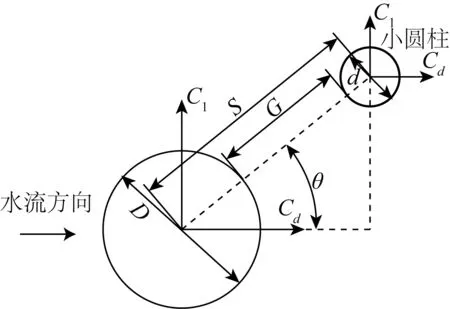
图2 圆柱布置Fig. 2 Arrangement of cylinders

图3 边界层网格Fig. 3 Mesh of boundary layer

本文利用有限体积法离散控制方程，压力速度耦合采用Simple算法，对流项采用二阶迎风格式，扩散项采用二阶迎风格式，时间离散采用全隐士格式。采用非结构化网格，为了精确模拟边界层处流场特征，对圆柱周围网格进行了加密处理，边界层网格如图3所示。

2.2边界条件

本文的进口条件为均匀来流u=0.39 m/s，出口条件为自由出流，圆柱表面为无滑移壁面边界，上下边界条件为对称边界，时间步长取为0.002 5 s，单个步长内迭代40次。

3 数值模拟和结果分析

3.1数学模型验证

1)单圆柱模型验证

本文选择的是κ-ε模型中的RNG模型，为了验证本文选择的湍流模型、参数设置和网格划分的准确性，首先进行了Re为3 900的单圆柱绕流过程模拟。在边界层的划分阶段，需要设置首层厚度、增长因子和层数，且为保证结果的准确性，边界层的厚度应大于实际流体边界层的厚度。其中首层厚度的设置需要在以往经验的基础上进行估计和调整，通常需要先确定y+值，再根据经验公式y+=0.172×Re0.9×(y/D)求得首层厚度y，对此边界层厚度下的圆柱绕流现象进行模拟，根据模拟结果再对y进行调整。

为选取合适的y+值，本文设计了A、B、C组工况。由A组工况可知，y+值为5时，本文模拟结果与前人计算结果最为接近，因此y+值设置为5。为了确定合适的圆柱节点数，本文设计了B组工况。由B组工况可知，圆柱节点数为80时已经能够满足计算需要。C组工况研究了边界层数对绕流结果的影响，由C组工况可知，边界层数对绕流结果影响较小，为保证边界层厚度，本文选取边界层为12层。三组工况及结果对比如表1所示。

表1 计算工况及结果对比Tab.1 Computation conditions and results comparison

从表1可以看出，圆柱节点数和边界层层数对单圆柱绕流的影响较小，在保证计算效率和计算精度的前提下，本文模拟圆柱绕流时采用A1的条件。在A1条件下将模拟结果与Re相同的物理模型实验结果[5-6]和数值模拟结果[7-9]进行了对比，结果如表2所示。

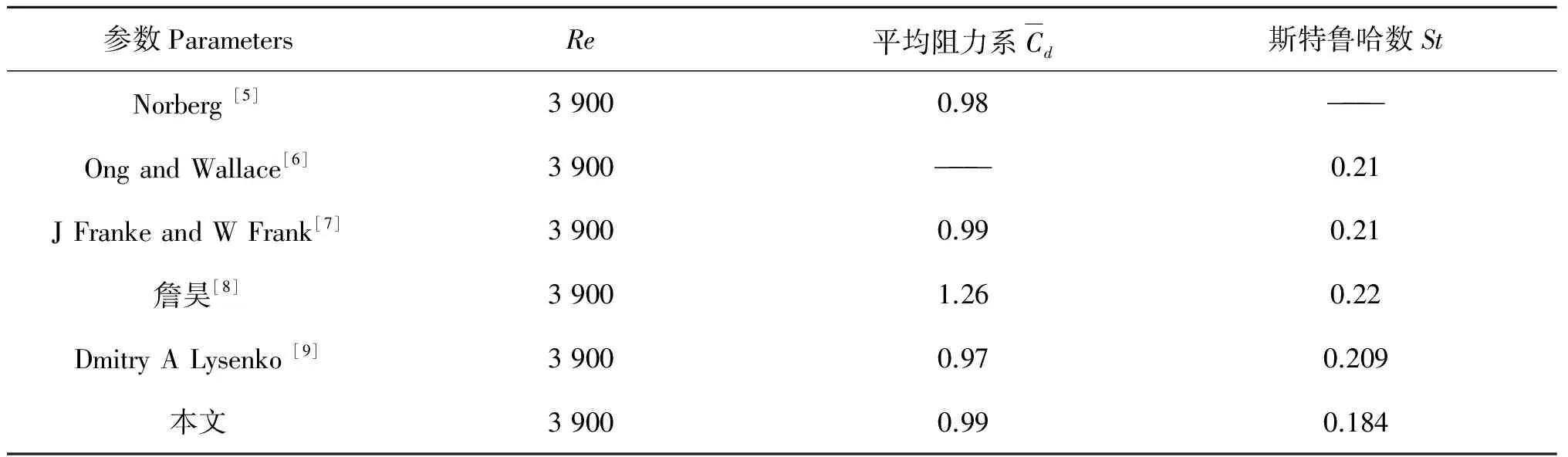
表2 单圆柱模型验证Tab. 2 Model validation of single cylinder

表2对比表明，Re处于亚临界区时，St稳定在0.2附近，平均阻力系数稳定在1.0附近。本文St数为0.184，平均阻力系数为0.99，和已有结果较为一致，因此本文的模拟方法是可行的。

2)双圆柱模型验证

为验证本文选取的模型在模拟双圆柱绕流时的可行性，本文模拟了不等直径并列双圆柱的绕流现象，并将两柱的平均阻力系数、平均升力系数、均方根升力系数和St与毕贞晓[10]和崔肖娜[11]的结论进行了比较。比对结果如表3所示。

表3 并列双柱模型验证(Re=3 900，d/D=0.5，G/D=2.0)Tab. 3 Model validation of two side-by-side cylinders for Re=3 900，d/D=0.5，G/D=2.0

由表3可以看出，在同种工况下，本文模拟结果与他人给出的结果差异较小，说明本文所建立的模型在模拟不等直径双圆柱绕流时是可行的。

3.2结果及分析

1)漩涡脱落形态

当d/D=0.5，G/D=2.0，θ=0°～180°时的尾流形态如图4所示。

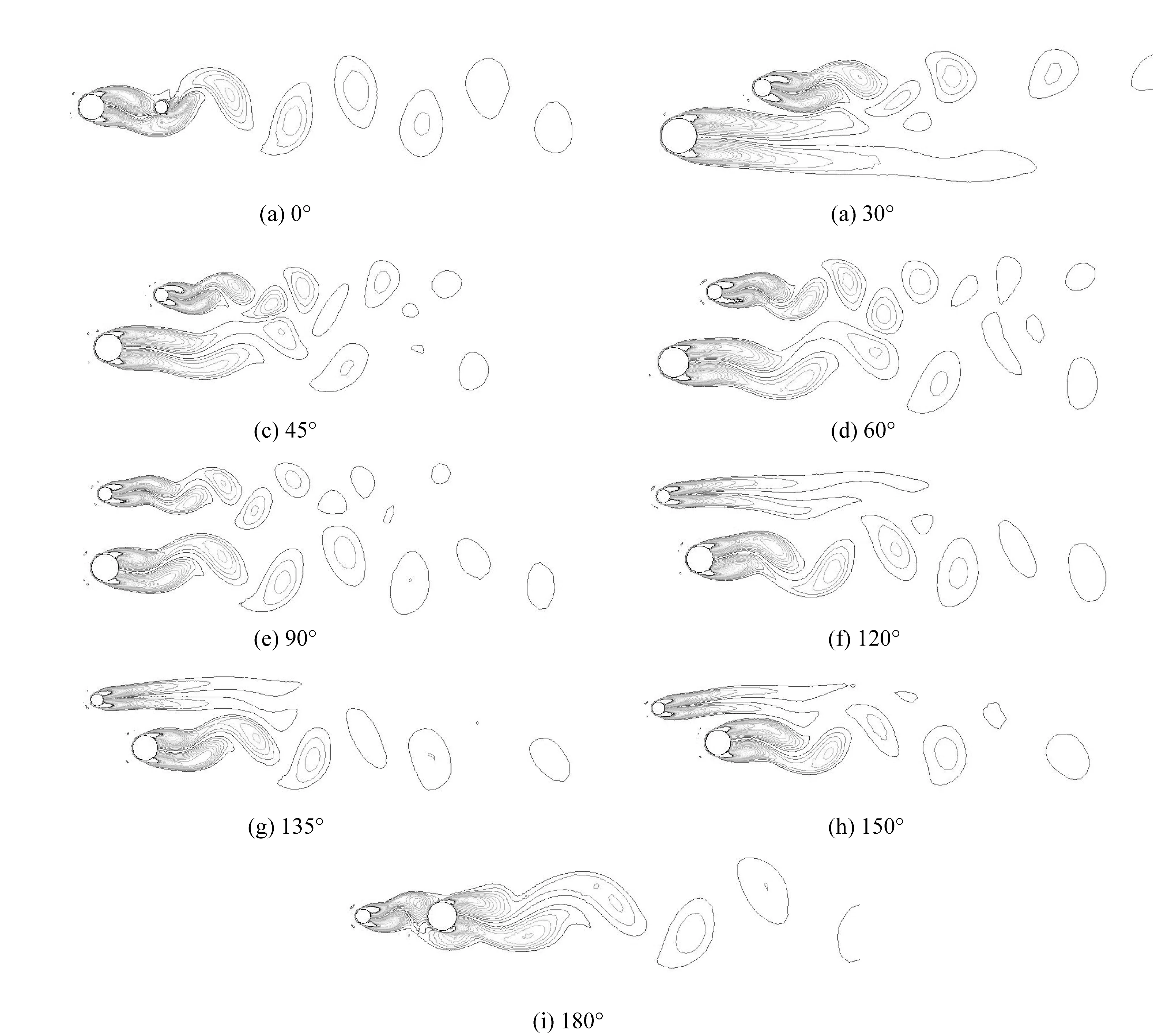
图4 尾流形态Fig. 4 Instantaneous vorticity contours

由图4可知，θ=0°时，两柱后方为单一涡脱落形态，两柱后方有单一涡脱落形态，小柱涡脱落对大柱影响较小，尾流与单圆柱绕流的尾流相似；θ=30°时，小柱后方有稳定漩涡脱落产生，大柱涡脱落受到干扰；θ=45°～90°时，在间隙流的作用下，两柱后方均有漩涡脱落，尾流中有两列涡街；θ=120°～150°时，大柱后有稳定漩涡脱落，小柱涡脱落受到抑制；θ=180°时，小柱涡脱落受大柱影响被抑制，大柱后有稳定漩涡脱落。

2)斯特鲁哈数St

St(Strouhal Number)数反应的是涡脱落频率f的大小，St与涡脱落频率f的关系如下：

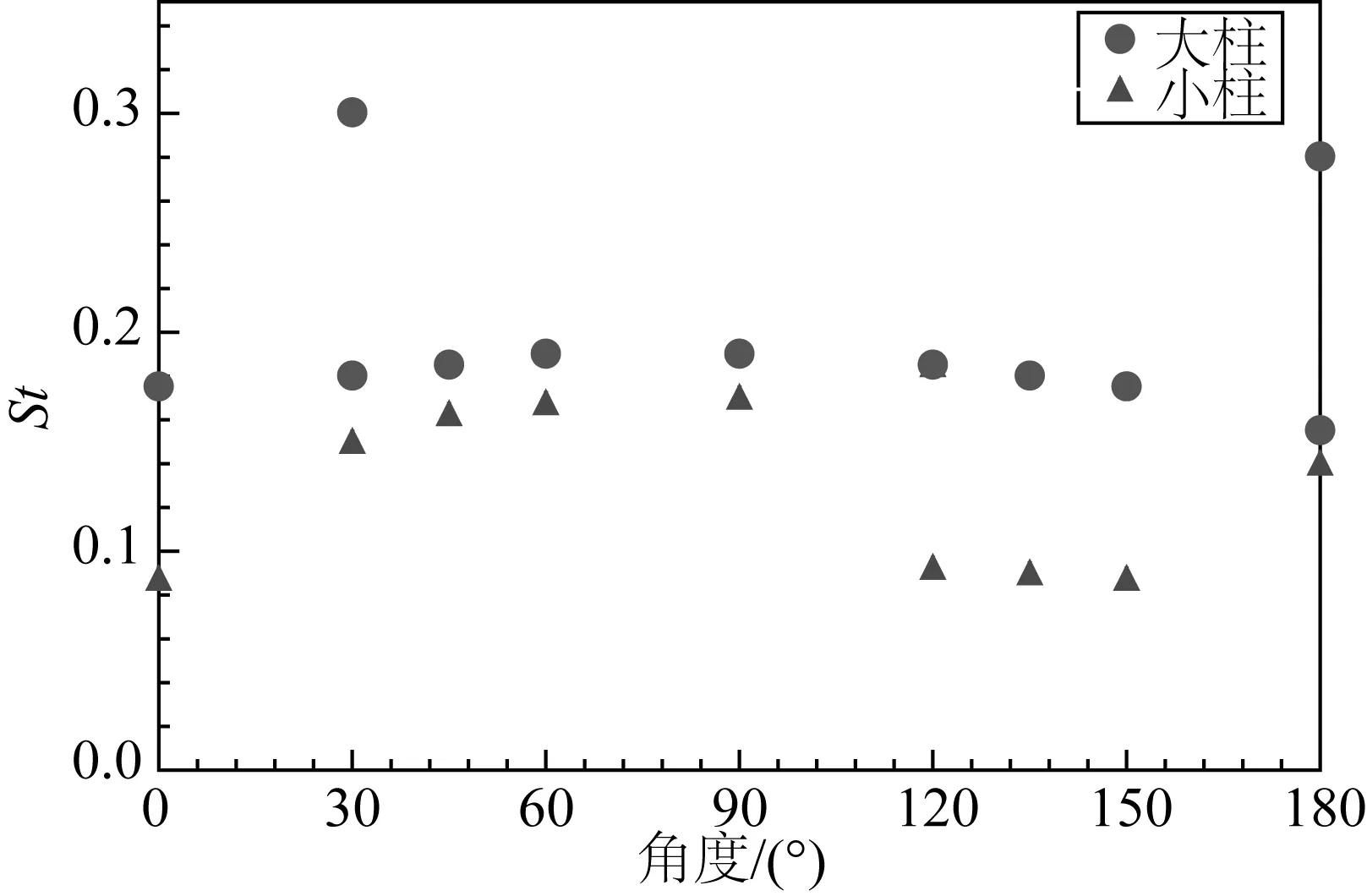
图5 St数Fig. 5 Variation of the Strouhal number

由于漩涡脱落的周期和升力系数变化的周期相同，因此对升力系数进行快速傅里叶变换(FFT)可以求得漩涡脱落频率，进而得到St数，图5给出了两圆柱St数随角度的变化。

由图5可知，随着θ的从小到大，St1先增大后减小，且在θ=30°和180°时有两个值，说明此时大柱有两个涡脱落频率，其中较大的一个频率与小柱相同，是由间隙流诱导产生，较小的一个由大柱自身的漩涡脱落引起；St2关于90°呈明显的不对称，在θ=120°～150°时明显小于其它角度，为St1的一半，说明此时小柱的涡脱落频率与大柱涡脱落频率相同。

3)平均阻力、升力系数

阻力系数和升力系数是反映圆柱水动力特性的重要参数，分别表征圆柱横向和纵向受力变化。图6、图7给出了不同角度下两圆柱的平均阻力系数和平均升力系数。

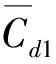
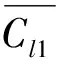
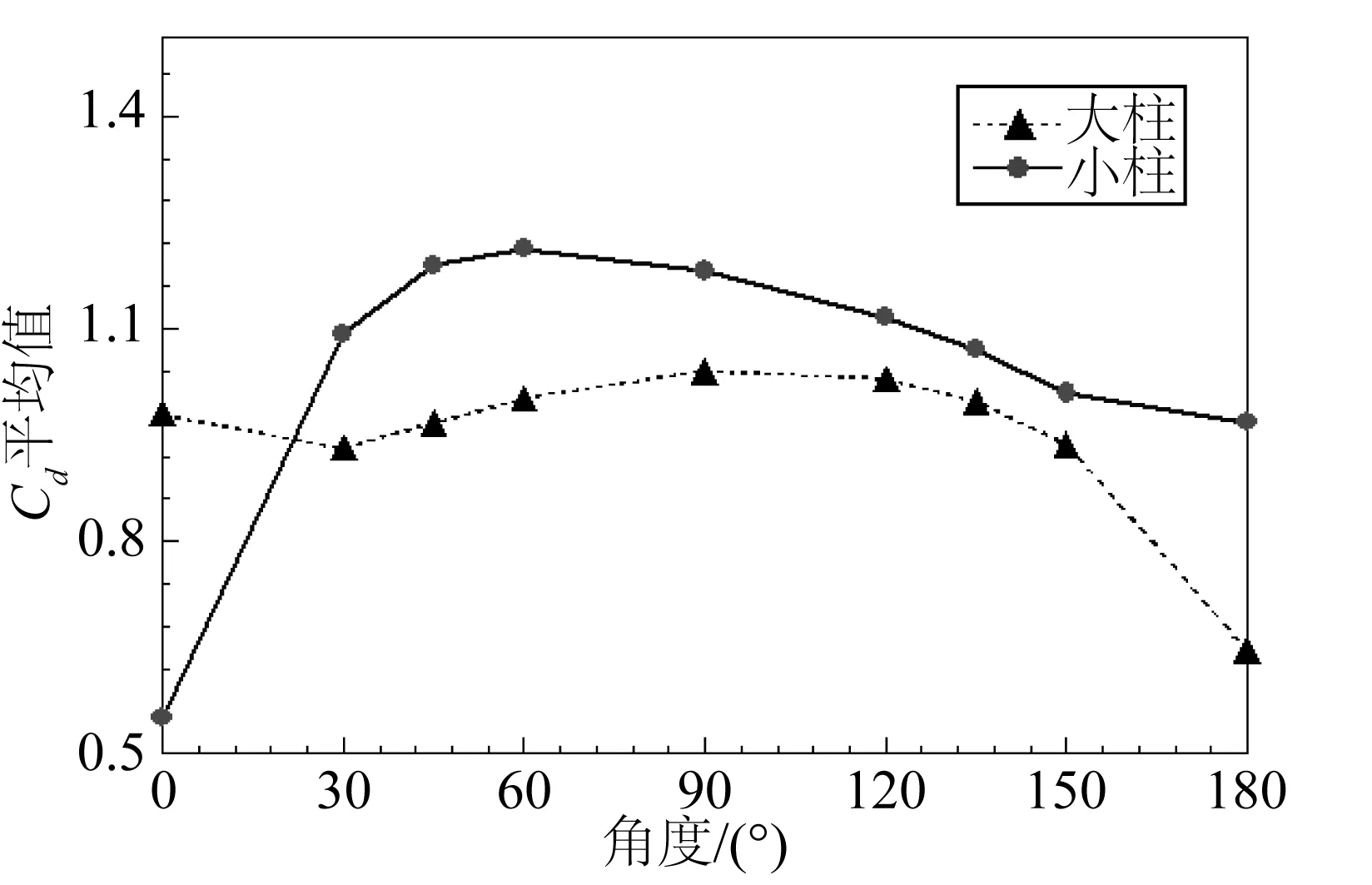
图6 平均阻力系数Fig. 6 Variation of mean drag force coefficient

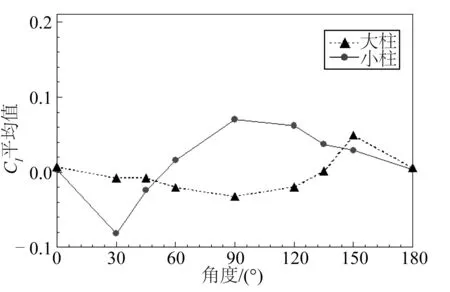
图7 平均升力系数Fig. 7 Variation of mean lift force coefficient

4 结 语

针对错列双柱体结构排列形式，利用Fluent软件中的κ-ε湍流模型对不等直径双圆柱的绕流过程进行了模拟，Re取为3 900，分析了在d/D=0.5，G/D=2.0情况下θ的变化对双圆柱绕流尾流形态、升阻力系数的影响，得到如下结论：

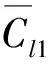
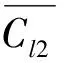
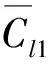
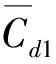
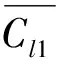
[1] TSUTSUI T, IGARASHI T, KAMEMTOT K. Interactive flow around two circular cylinders of different diameters at close proximity. Experiment and numerical analysis by vortex method[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1997:279-291.

[2] ZHAO M, CHENG L, TENG B, et al. Hydrodynamic forces on dual cylinders of different diameters in steady currents[J]. Journal of Fluids and Structures, 2007, (1):59-83.

[3] ZHOU Yu, FENG S X, Alam Md Mahbub, et al. Reynolds number effect on the wake of two staggered cylinders[J].Physics of Fluids, 2009,21(12):1-14.

[4] 冯志鹏,臧峰刚,张毅雄. 两交错排列弹性管的流致振动特性研究[J]. 应用力学学报,2015,32(1):1-5.(FENG Zhipeng, ZANG Fenggang, ZHANG Yixiong. Investigation of flow induced vibration characteristics in two staggered flexible tubes[J]. Chinese Journal of Applied Mechanics, 2015,32(1):1-5. (in Chinese))

[5] NORBERG C. Effects of Reynolds number and low-intensity free-stream turbulence on the flow around a circular cylinder [J]. Department of Applied Thermodynamics and Fluid Mechanics, 1987, 87(2).

[6] ONG L, WALLACE J. The velocity field of the turbulent very near wake of a circular cylinder [J]. Experiments in Fluids, 1996, 20: 441-453.

[7] FRANKE J, FRANK W. Large eddy simulation of the flow past a circular cylinder atRe=3 900 [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2002, 90: 1 191-1 206.

[8] 詹昊,李万平,方秦汉,等. 不同雷诺数下圆柱绕流仿真计算[J].武汉理工大学学报，2008，30(12):129-132. (ZHAN Hao, LI Wanping, FANG Qinhan, et al. Numerical simulation of the flow around a circular cylinder at varies Reynolds Number [J]. Journal of Wuhan University of Technology, 2008, 30(12):129-132. (in Chinese))

[9] DMITRY A, LYSENKO, IVAR S, et al. Large-eddy simulation of the flow over a circular cylinder at Reynolds Number 3 900 using the OpenFOAM Toolbox[J].Flow, Turbulence and Combustion, 2012,89(4): 491-518.

[10] 毕贞晓. 不等直径并列双圆柱绕流的受力分析和湍流特性研究[D].上海: 上海应用技术学院, 2015.(BI Zhenxiao. Investigation of force analysis and turbulent characteristics in the flow past two side-by-side circular cylinders with different diameters[D]. Shanghai: Shanghai Institute of Technology,2015.(in Chinese))

[11] 崔肖娜. 并列双圆柱绕流的水动力特性研究[D].青岛: 中国海洋大学, 2014.(CUI Xiaona. Hydrodynamic characteristics of viscous flow past two side-by-side cylinders[D].Qingdao: Ocean University of China,2014. (in Chinese))

Numerical study on viscous flow around two staggered cylinders with different diameters

YU Dingyong, LI Yujia, MA Zhaohui, LI Long

(Engineering Academy, Ocean University of China, Qingdao 266100，China)

1005-9865(2017)02-0098-07

TV143

A

10.16483/j.issn.1005-9865.2017.02.014

2016-06-06

山东省重点基金资助项目(ZR2013EEZ002)

于定勇(1964-)，男，山东省青岛人，教授，博士。主要从事海洋动力与结构物和岸滩作用的研究。E-mail：dyyu01@126.com