计算流体力学模拟街道峡谷特征和风向对细颗粒物污染扩散的影响*
刘建峰 王宝庆 牛宏宏 刘博薇 任自会 陈荣会 王泽北
(南开大学环境科学与工程学院,天津 300071)
计算流体力学模拟街道峡谷特征和风向对细颗粒物污染扩散的影响*
刘建峰 王宝庆#牛宏宏 刘博薇 任自会 陈荣会 王泽北
(南开大学环境科学与工程学院,天津 300071)
街道峡谷结构和风向会对街道峡谷内的污染物浓度和扩散特征带来一定影响。利用计算流体力学(CFD)软件,针对街道峡谷高宽比、建筑物间隔(建筑物间空隙与街道总长度的比值)和风向对街道峡谷内细颗粒物扩散的影响进行数值模拟。模拟结果表明,建筑物间隔为20%,风向为北风,风速为3m/s,街道峡谷高宽比分别为1∶2、1∶1和2∶1时,街道中心线距地面1.5m高度细颗粒物最大质量浓度分别位于-19.3、-88.0、-19.3m(以与街道中心点的距离计,正值表示在街道中心点以东,负值表示在街道中心点以西,下同)位置,为37.5、46.4、28.4μg/m3。街道峡谷高宽比为1∶1,风向为北风,风速为3m/s,建筑物间隔分别为0、20%和40%时,街道中心线距地面1.5m高度的细颗粒物最大质量浓度分别位于148.0、-92.3、-186.7m位置,为88.1、31.6、33.7μg/m3。街道峡谷高宽比为1∶1,建筑物间隔为20%,风速为3m/s,且分别处于西风、北风和西南风时,街道中心线距地面1.5m高度的细颗粒物最大质量浓度分别位于165.3、58.0、1.5m位置,为10.6、11.2、16.0μg/m3。可见,CFD模拟近地面污染物扩散时应考虑街道峡谷结构和风向的影响。
街道峡谷 细颗粒物扩散 计算流体力学 结构
最近几年,许多流行病学的研究显示,道路污染能对人群健康产生不利影响,可能引起呼吸系统疾病、心血管病、出生缺陷、癌症和死亡[1]。随着机动车数量的迅猛增加,空气污染问题在中心城区尤为严峻。街道两侧高楼耸立,与狭长的街道形成“街道峡谷”建筑结构。街道峡谷的特点不利于峡谷内的污染物扩散稀释,从而导致局部区域污染加重[2-3]。街道峡谷两旁的建筑结构决定着峡谷内风场的流动类型,车辆排放的污染物浓度在一定时间内得以聚集,可能导致峡谷内的空气质量恶化[4-5]。为了解街道峡谷内的空气流场和污染物扩散模式,一般采用计算机模拟[6-7]、风洞试验[8-9]或现场测量[10-12]进行研究。
OKAMOTO等[13]发展了2D数值模型AQSM用以研究街道峡谷污染分布,该模型包含两个模块,一个是风场模块,另一个是扩散模块。ADDISON等[14]提出了预测街道峡谷内污染物空间分布的理论依据。XIA等[15]利用2D风场模型和拉格朗日模型,研究建筑物结构和流场对污染物扩散的影响。国内研究者利用计算流体力学(CFD)软件对街道峡谷污染物扩散进行了相关研究[16-23],针对的污染物主要是CO、NOx、PM10和碳氢化合物(HC)。但是关于街道峡谷内细颗粒物污染的研究不多,污染扩散规律还需要进一步探究。
由于计算机性能的提高和CFD软件的开发,对街道峡谷复杂结构内流场和污染物扩散的模拟越来越精确[24]。如果初始条件和边界条件已知,对任何结构、不同环境条件下的街道峡谷,CFD软件均可进行模拟。而现场测量只能测得现场条件下的速度场和污染物浓度场;风洞试验虽可对不同结构下的峡谷速度场和污染物浓度场进行模拟测量,但需要花费大量费用。
本研究采用CFD软件,对不同街道结构和风向条件下的街道峡谷内的细颗粒物扩散进行模拟,并着重关注呼吸高度(1.5 m)处的细颗粒物浓度,为城市规划、交通规划及房屋设计提供借鉴。
1 研究对象
选取天津市南京路比较典型的路段——卫津路至万全道为研究对象。南京路位于天津市市区的中心位置,具有较大的车流量和较为严重的交通拥堵现象,由于两侧建筑物高大、人口密度相对集中,因此具有典型的城市街道峡谷特征。南京路是双向9车道城市主干道,街道总宽约50 m,其中机动车车道宽度约为28 m,两侧非机动车道和人行道总宽均为11 m,路段长度约为425 m,两侧建筑物平均高度约为70 m。
2 CFD模拟
2.1 模拟方程
流体流动受守恒定律支配,主要包括质量守恒定律、动量守恒定律和能量守恒定律。湍流模型是CFD的主要组成部分之一,主要包括以下几种模型:单方程模型、标准k—ε模型、重整群(RNG)k—ε模型、可实现性k—ε模型、标准k—ω模型、压力修正k—ω模型、雷诺应力(RSM)模型、大涡模拟(LES)模型等。
黄远东等[25]采用CFD软件Fluent中7种不同的湍流模型对城市街道峡谷内的气流运动和污染物扩散进行了数值模拟,将模拟结果与风洞试验数据进行对比分析表明:标准k—ε模型的总体预测效果最好;RNGk—ε模型、可实现性k—ε模型以及RSM模型的预测效果次之;而标准k—ω模型和单方程模型的预测效果较差。谢海英等[26]通过数值模拟和风洞试验,得出了相似的结论。
在街道峡谷问题的研究中,由于建筑物近壁区内雷诺数较低,湍流应力小,导致湍流不能充分发展,需要引入壁面函数进行近壁面流动修正。方平治等[27]通过同济大学TJ-2风洞模拟研究得出,标准壁面函数适用于粗糙度较小的风场模拟,修正的壁面函数适用于粗糙度较大的风场模拟。
Fluent除了可以求解流体(连续相)流动问题之外,还可以求解存在颗粒、液滴、气泡等离散相的多相流问题。求解多相流问题一般有两种方法,分别为多相流模型和离散相(DPM)模型。颗粒运动在Fluent中可通过DPM模型计算[28-29]。
本研究利用CFD软件Fluent 14.0进行街道峡谷内污染物扩散的三维湍流数值模拟,模型的建立和网格划分是利用Fluent的前处理软件ICEM CFD完成。对街道峡谷模拟的湍流模型选择标准k—ε模型,并采用标准壁面函数法消除近壁面流动的影响。在DPM模型应用中采用气固耦合的方式进行求解,在进行流场运算的同时进行颗粒相的运算。
2.2 计算区域的选择和几何模型的建立
如图1所示,计算区域安全距离选择入口边界至街道峡谷5H处,两侧至街道峡谷均为5H,街道峡谷至出口边界为10H,总高度为8H。
以实际街道卫星图为原型,将街道峡谷进行适当简化并建立几何模型。几何建模结果如图2所示。
由于本研究的区域模型较不规则,因此选用非结构化网格进行模型的网格划分。为减少计算量并且不影响计算精度,将入口及街道峡谷处进行了一定的加密处理,在近地面处采用棱柱网格。最终的网格划分结果为:网格单元总数约为370万个,节点数约为71万个,最小网格尺寸约为1 m。经Fluent网格检验,无负体积出现,表明该网格可以进行数值计算。
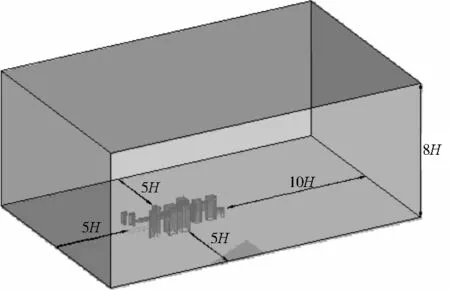
注:H为街道峡谷高度,m。图1 街道峡谷模拟计算区域Fig.1 Computational area of street canyon
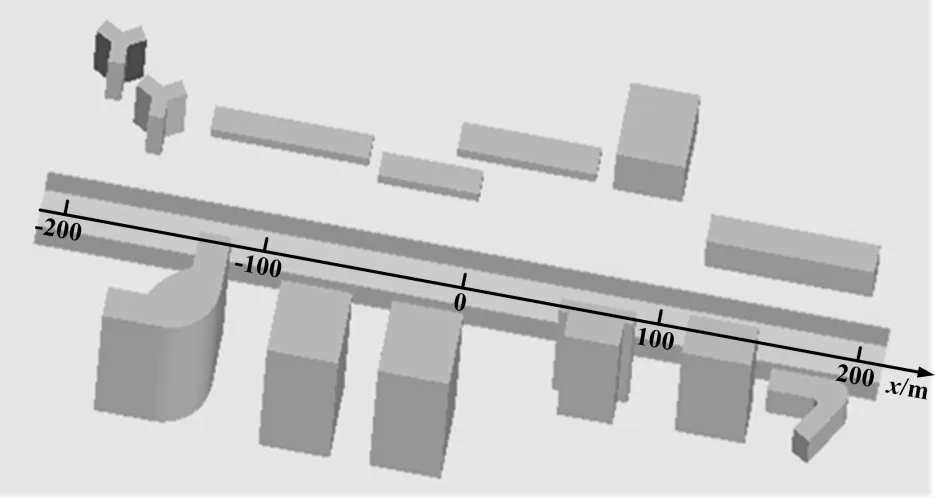
注:x为街道中心线上距街道中心点的的距离,m,中心点西侧为负,东侧为正。
图2街道峡谷的几何模型
Fig.2 Geometric model of street canyon
2.3 边界条件和源强的确定
入口边界条件:速度入口平均风速遵循指数律分布,如式(1)所示。
Ui=U0(Zi/Z0)α
(1)
式中:Ui和U0分别为高度Zi和Z0(10 m)处对应的平均风速,m/s;α为大气稳定度参数。根据天津市平均风速,U0取3.0 m/s,α取0.22。
出口边界条件:设置为充分发展流动。下边界为无滑移固体壁面,两侧边界和上边界为对称边界。建筑物壁面为无滑移固体壁面。
刘川等[30]对深圳市机动车细颗粒物排放因子进行了测试研究,利用线性回归,计算得出重型车、轻型车的细颗粒物综合排放因子分别为160.8、15.7 mg/(km·辆)。天津市和平区南京路研究路段高峰期间车流量为3 600辆/h,轻型车与重型车数量比约为11∶1,计算得出细颗粒物源强为1.18×10-5kg/s。
2.4 区域风向分布
由于全年风向未全面获取,分别绘制2015年8月和2016年1月的风玫瑰图代表夏季和冬季的风向分布,如图3、图4所示。由图3、图4可以看出,天津市在夏季和冬季的主导风向不同,但北风和西南风是主导风向。因此,在讨论风向对街道峡谷细颗粒物扩散的影响时,模拟了北风和西南风。
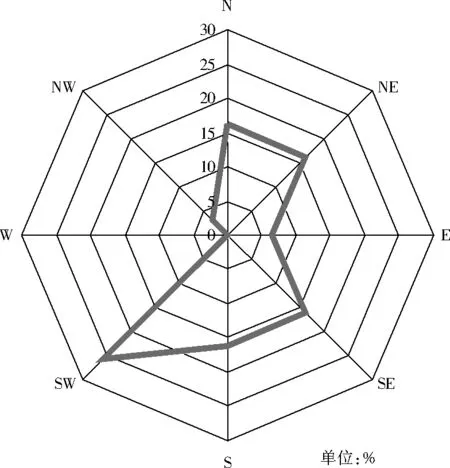
图3 天津市2015年8月的风玫瑰图Fig.3 Tianjin’s wind rose in August 2015

图4 天津市2016年1月的风玫瑰图Fig.4 Tianjin’s wind rose in January 2016
3 分析与讨论
3.1 研究区域背景值
选择2015年10月和11月空气中细颗粒物浓度较低的两天,在街道峡谷内无机动车通过的情况下利用光学颗粒物粒径谱仪(OPS)进行研究区域背景值测量,测量结果如表1所示。由表1可以看出,距地面不同高度处,街道峡谷中心线的细颗粒物背景值随高度的增加而降低。

表1 不同高度处街道峡谷中心线的细颗粒物背景值
3.2 街道峡谷高宽比(H/W)的影响
在风向为北风,风速3 m/s,建筑间隔(建筑物间空隙与街道总长度的比值)为20%的条件下,设置3种不同的街道峡谷H/W(1∶2、1∶1、2∶1),依次对应宽峡谷、理想峡谷和深窄型峡谷。模拟时街道宽度不变,调整建筑物高度。
街道峡谷H/W分别为1∶2、1∶1、2∶1时,0.2、1.0、1.5 m高度处街道中心线细颗粒物浓度的模拟结果见图5,最大浓度及位置见表2。
由表2可以得出,不同H/W都呈现出距地面越近,细颗粒物最大浓度越高的特征。在街道峡谷H/W为1∶2时,不同高度处街道中心线细颗粒物的最大浓度出现在x=-19.3 m位置;其中,距地面1.5 m高度处,细颗粒物最大质量浓度为37.5 μg/m3。而街道峡谷H/W分别为1∶1、2∶1时,距地面1.5 m高度处,街道中心线细颗粒物最大质量浓度均分别出现在x=-88.0、-19.3 m位置,分别为46.4、28.4 μg/m3。
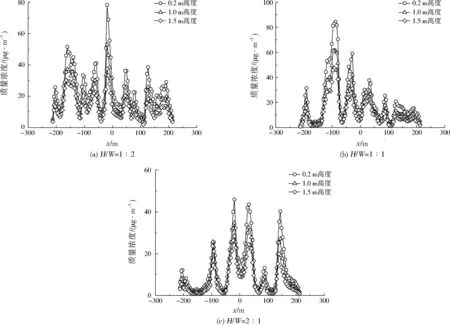
图5 街道峡谷H/W=1∶2、1∶1、2∶1时,不同高度处街道中心线的细颗粒物质量浓度Fig.5 Fine particulate matters concentration of street central line for H/W of 1∶2,1∶1 and 2∶1 at different heights above ground

参数H/W=1∶20.2m高度1.0m高度1.5m高度H/W=1∶10.2m高度1.0m高度1.5m高度H/W=2∶10.2m高度1.0m高度1.5m高度x/m-19.3-19.3-19.3-88.0-92.3-88.0-19.3-19.3-19.3细颗粒物最大质量浓度/(μg·m-3)78.352.937.584.361.446.446.034.828.4
街道峡谷H/W通过影响建筑物顶部绕流和建筑物间隙流,从而影响细颗粒物扩散。在街道峡谷H/W=1∶2的条件下,由于街道峡谷建筑物相对较低,建筑物顶部绕流较强,建筑物间隙流较弱,街道峡谷内部近地面处涡流明显且分布均匀;在街道峡谷H/W=1∶1的条件下,建筑物间隙流增强,进入街道峡谷的气流量相应较大,建筑物背风面产生的回流较少,穿过街道峡谷另一侧建筑间隙的气流增多;在街道峡谷H/W=2∶1的条件下,建筑物间隙流进一步加强,建筑物顶部绕流相对减弱,街道峡谷内流场分割成低速和高速相间的流场形式,流场分布比较复杂。可见,随着街道峡谷H/W的增大,建筑物间隙流增大,建筑物顶部绕流减小,近地面处细颗粒物浓度大体减小。
3.3 建筑物间隔的影响
在风向为北风、风速为3 m/s、街道峡谷H/W=1∶1的条件下,建筑物间隔(建筑物间空隙与街道总长度的比值)分别为0、20%、40%时,0.2、1.0、1.5 m高度街道峡谷中心线细颗粒物分布见图6,最大浓度及位置见表3。
由表3可以看出,在不同建筑物间隔下都呈现出距地面越近,细颗粒物最大浓度越高的特征。在建筑物间隔为0时,不同高度处街道中心线细颗粒物的最大浓度集中在x≈150 m位置;其中,距地面1.5 m高度处,细颗粒物最大质量浓度出现在x=148.0 m位置,为88.1 μg/m3。而建筑物间隔为20%和40%时,距地面1.5 m高度处,街道中心线细颗粒物的最大质量浓度分别出现在x=-92.3、-186.7 m位置,为31.6、33.7 μg/m3。
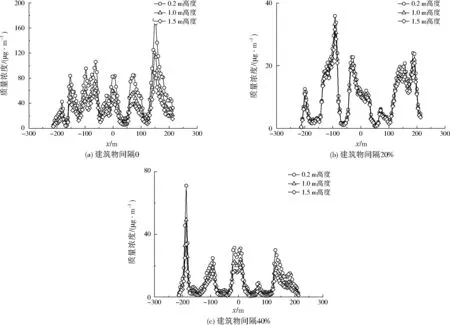
图6 建筑物间隔为0、20%、40%时,不同高度处街道峡谷中心线的细颗粒物质量浓度Fig.6 Fine particulate matters concentration of street central line for architecture gap of 0,20%,40% at different heights above ground

参数建筑物间隔00.2m高度1.0m高度1.5m高度建筑物间隔20%0.2m高度1.0m高度1.5m高度建筑物间隔40%0.2m高度1.0m高度1.5m高度x/m148.0152.0148.0-92.3-92.3-92.3-186.7-186.7-186.7细颗粒物最大质量浓度/(μg·m-3)173.0114.088.135.933.331.671.149.433.7
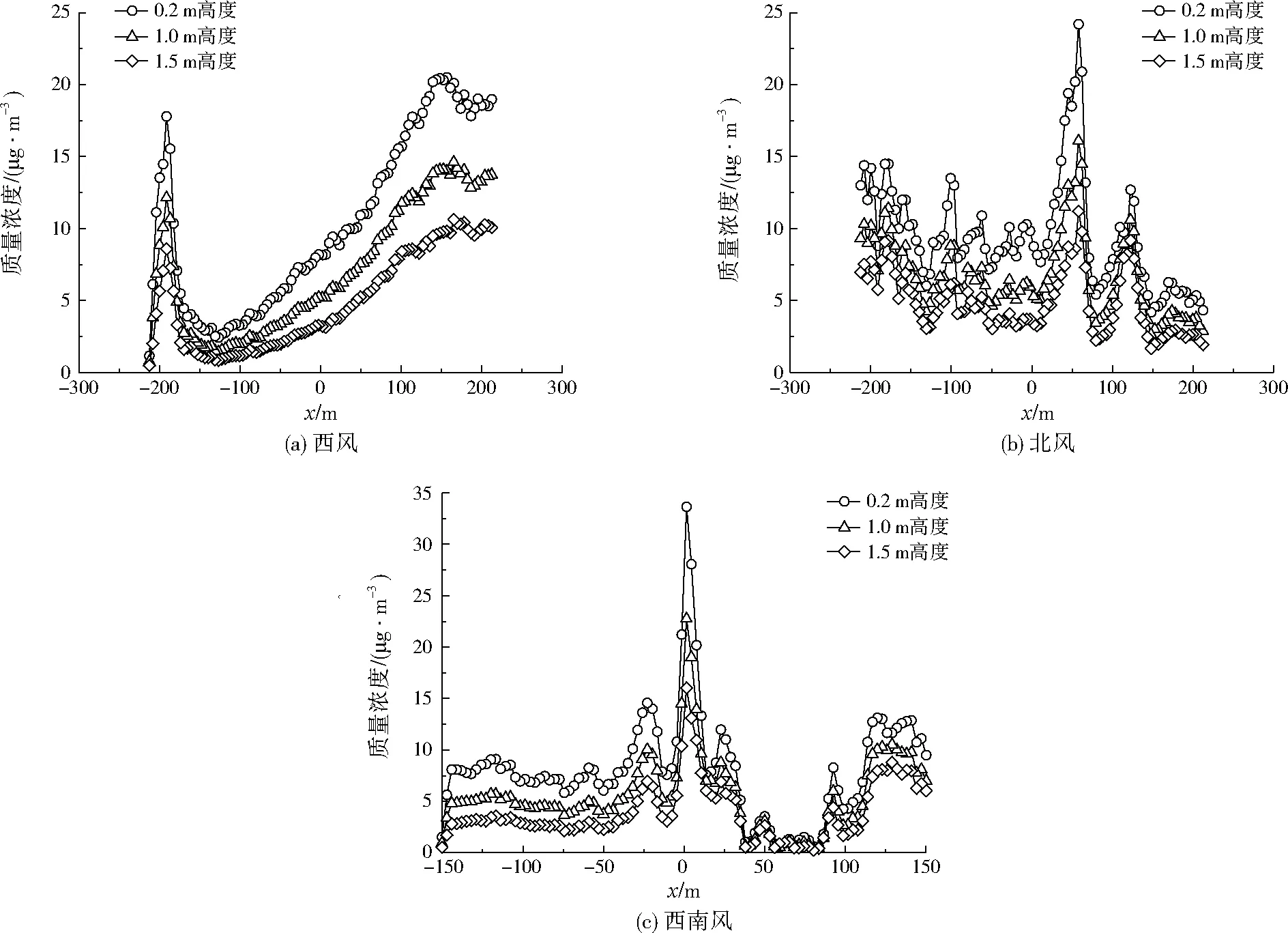
图7 风向为西风、北风和西南风时,不同高度处街道峡谷中心线的细颗粒物质量浓度Fig.7 Fine particulate matters concentration of street central line for wind direction of west, north and southwest at different heights above ground
当建筑物间隔为0时,近地面气流从街道峡谷两侧产生绕流,分别产生一个顺时针旋涡和一个逆时针旋涡,且两个旋涡的回旋气流通过另一侧建筑物间隔进入街道峡谷。街道峡谷进气气流主要是两侧回旋气流,其由建筑物间隔进入,穿过街道并沿着建筑物背风面产生“爬墙效应”,最终向街道峡谷两端运动汇入绕流气流。总体而言,街道峡谷内部流场相对稳定,涡流较少,紊流程度低,不利于污染物的扩散。街道峡谷内部细颗粒物主要在建筑物迎风面区域聚集,且细颗粒物分布连续,污染浓度比较均匀。当建筑物间隔为20%时,近地面气流同样从街道峡谷两侧绕流并产生回流,与建筑物间隔为0的情况相比,街道峡谷建筑物间隙流气流量增大,气流交换率增大。同时,在来流气流与反向的回旋气流相互作用下,产生一定数量的涡流,街道峡谷内部紊流程度增加,对流扩散作用相对增强。细颗粒物浓度分布不连续且不均匀,相比建筑物间隔为0的情况,细颗粒物浓度明显减小。当建筑物间隔为40%时,街道峡谷流场与建筑物间隔为20%时差异明显。随着建筑物间隔的进一步加大,建筑物间隙流的气流量进一步增大,由于气流直接穿过街道并流出街道峡谷,使街道峡谷两侧的回流旋涡受到破坏,街道峡谷内部涡流较少,在街道峡谷外侧建筑物背风面形成涡流。街道峡谷内部气流场及细颗粒物分布被间隙气流切割而呈现分段特征,即间隙处风速大,细颗粒物浓度低,无间隙处风速小,对流扩散作用较小,细颗粒物聚集产生相对严重的局部污染。
总体而言,随着建筑物间隔的增加,街道峡谷内外气流的交换率增加,街道峡谷内部的对流扩散作用增强,街道峡谷中心线的细颗粒物基本呈现降低趋势,但是由于间隙流的作用,相比于建筑物间隔为20%时,建筑物间隔为40%时的街道峡谷中心线的细颗粒物浓度在局部位置有所增加。
3.4 风向的影响
在风速为3 m/s,街道峡谷H/W=1∶1,建筑物间隔为20%的条件下,设置不同风向(包括西风、北风和西南风),距地面高度0.2、1.0、1.5 m处街道峡谷中心线细颗粒物分布见图7,最大浓度及位置见表4。

表4 风向为西风、北风和西南风时,不同高度处街道峡谷中心线的细颗粒物最大浓度及位置
由表4可以得出,在不同风向下都呈现出距地面越近,细颗粒物浓度越高的特征。风向为西风时,不同高度处街道中心线细颗粒物的最大浓度集中在x≈160 m位置;其中,距地面1.5 m高度处,细颗粒物最大质量浓度出现在x=165.3 m位置,为10.6 μg/m3。风向为北风和西南风时,距地面1.5 m高度处,街道中心线细颗粒物的最大质量浓度分别出现在x=58.0、1.5 m位置,为11.2、16.0 μg/m3。
在不同风向下,街道峡谷由于其自身的结构特点,均会产生不同程度的“街道峡谷效应”,即气流通过建筑物间隔和街道峡谷时,出现风速增大(增大到约6 m/s左右)、风向改变的普遍特征。风向不同,街道峡谷内的气流运动规律不同:风向为西风时,街道峡谷内部流场相对稳定;风向为西南风时,街道峡谷流场呈现出明显的分段特征;风向为北风时,涡流、紊流现象较为明显,街道峡谷内湍流程度较大。因此,街道峡谷内细颗粒物呈现不同的空间分布特征,在水平方向上细颗粒物主要随运动气流迁移并累积。风向为西风时,街道峡谷内扩散作用强,细颗粒物浓度低;风向为北风时,涡流中心区域污染物容易积聚,局部污染在建筑物背风面较为严重。在垂直方向上,随着水平高度的升高,细颗粒物浓度逐渐降低,相比西风,风向为北风时街道峡谷内风速小、细颗粒物水平迁移慢,垂直方向扩散速度相对较慢。因此,风向为西风或者风向与街道峡谷轴向夹角较小时更有利于街道峡谷内细颗粒物的稀释扩散。
4 结 论
(1) 随着街道峡谷H/W的增大,建筑物间隙流增强,建筑物顶部绕流相对减弱。建筑物间隔为20%,风向为北风,风速为3 m/s,街道峡谷H/W分别为1∶2、1∶1和2∶1时,1.5 m高度处,街道中心线细颗粒物最大质量浓度分别位于x=-19.3、-88.0、-19.3 m位置,为37.5、46.4、28.4 μg/m3。
(2) 随着建筑物间隔的增加,街道峡谷内外气流的交换率增加,街道峡谷内部的对流扩散作用增强。街道峡谷H/W为1∶1,风向为北风,风速为3 m/s,建筑物间隔分别为0、20%和40%时,街道中心线距地面1.5 m高度的细颗粒物最大质量浓度分别位于x=148.0、-92.3、-186.7 m位置,为88.1、31.6、33.7 μg/m3。
(3) 风向为西风时,街道峡谷内的扩散作用强,细颗粒物浓度最低。街道峡谷H/W为1∶1,建筑物间隔为20%,风速为3 m/s,且分别处于西风、北风和西南风时,街道中心线距地面1.5 m高度的细颗粒物最大质量浓度分别位于x=165.3、58.0、1.5 m位置,为10.6、11.2、16.0 μg/m3。
[1] PETERS A,VON KLOT S,HEIER M,et al.Exposure to traffic and the onset of myocardial infarction[J].New England Journal of Medicine,2004,351(17):1721-1730.
[2] CHAN A T,AU W T,SO E S.Strategic guidelines for street canyon geometry to achieve sustainable street air quality - part Ⅱ: multiple canopies and canyons[J].Atmospheric Environment,2003,37(20):2761-2772.
[3] BADY M,KATO S,HUANG Hong.Towards the application of indoor ventilation efficiency indices to evaluate the air quality of urban areas[J].Building and Environment,2008,43(12):1991-2004.
[4] ZHOU Ying,LEVY J I.The impact of urban street canyons on population exposure to traffic-related primary pollutants[J].Atmospheric Environment,2008,42(13):3087-3098.
[5] WANG Peng,MU Hailin.Numerical simulation of pollutant flow and dispersion in different street layouts[J].International Journal of Environmental Studies,2010,67(2):155-167.
[6] AHMAD K,KHARE M,CHAUDHRY K K.Wind tunnel simulation studies on dispersion at urban street canyons and intersections - a review[J].Journal of Wind Engineering and Industrial Aerodynamics,2005,93(9):697-717.
[7] LI Xianxiang,LIU C H,LEUNG D Y,et al.Recent progress in CFD modelling of wind field and pollutant transport in street canyons[J].Atmospheric Environment,2006,40(29):5640-5658.
[8] BADY M,KATO S,TAKAHASHI T,et al.An experimental investigation of the wind environment and air quality within a densely populated urban street canyon[J].Journal of Wind Engineering and Industrial Aerodynamics,2011,99(8):857-867.
[9] GROMKE C,RUCK B.Influence of trees on the dispersion of pollutants in an urban street canyon - experimental investigation of the flow and concentration field[J].Atmospheric Environment,2007,41(16):3287-3302.
[10] GHENU A,ROSANT J M,SINI J F.Dispersion of pollutants and estimation of emissions in a street canyon in Rouen,France[J].Environmental Modelling & Software,2008,23(3):314-321.
[11] KUMAR P,GARMORY A,KETZEL M,et al.Comparative study of measured and modelled number concentrations of nanoparticles in an urban street canyon[J].Atmospheric Environment, 2009,43(4):949-958.
[12] MURENA F,VORRARO F.Vertical gradients of benzene concentration in a deep street canyon in the urban area of Naples[J].Atmospheric Environment,2003,37(35):4853-4859.
[13] OKAMOTO S,FU Chifu,YAMADA H,et al.Evaluation of a two-dimensional numerical model for air quality simulation in a street canyon[J].Atmospheric Environment,1996,30(23):3909-3915.
[14] ADDISON P S,CURRIE J I,LOW D J,et al.An integrated approach to street canyon pollution modelling[J].Environmental Monitoring & Assessment,2000,65(1/2):333-342.
[15] XIA Jiyang,LEUNG D Y.Pollutant dispersion in urban street canopies[J].Atmospheric Environment,2001,35(11):2033-2043.
[16] 施继红.城市道路平面交叉口交通污染分析及综合评价[D].长春:吉林大学,2012.
[17] 朱中伟.城市街道峡谷内机动车排放活性污染物扩散研究[D].上海:上海交通大学,2013.
[18] 郭振宇.城市街道峡谷内机动车尾气排放的PM2.5的对流扩散规律研究[D].济南:山东建筑大学,2013.
[19] 王建长.城市街道峡谷内机动车污染物扩散的数值模拟研究[D].济南:山东大学,2012.
[20] 熊胜益.城市街谷型交叉口内汽车尾气污染的试验及数值模拟研究[D].西安:西安建筑科技大学,2011.
[21] 柳靖.机动车尾气在街谷中分布规律及其对建筑环境的影响[D].哈尔滨:哈尔滨工业大学,2009.
[22] 赵静.基于多孔介质方法的城市街区汽车污染物对流扩散数值模拟研究[D].济南:山东建筑大学,2012.
[23] 杨国彬.街道峡谷机动车尾气污染扩散模拟研究[D].重庆:重庆工商大学,2007.
[24] SAGRADO A G,BEECK J V,RAMBAUD P,et al.Numerical and experimental modelling of pollutant dispersion in a street canyon[J].Journal of Wind Engineering and Industrial Aerodynamics,2002,90(4):321-339.
[25] 黄远东,王守生,金鑫,等.城市街道峡谷内污染物扩散模拟中不同湍流模型的比较研究[J].水动力学研究与进展,2008,23(2):189-195.
[26] 谢海英,张道方.湍流模型对预测街道峡谷污染物扩散的影响[J].环境科学与技术,2009,32(6):116-120.
[27] 方平治,顾明,谈建国.计算风工程中基于k—ε系列湍流模型的数值风场[J].水动力学研究与进展,2010,25(4):475-483.
[28] 李立清,胡蔷,黄贵杰,等.环栅喷淋泡沫塔欧拉-离散相模型三相除尘模拟[J].中国电机工程学报,2012,32(5):68-77.
[29] BOWKER G E,BALDAUF R,ISAKOV V,et al.The effects of roadside structures on the transport and dispersion of ultrafine particles from highways[J].Atmospheric Environment,2007,41(37):8128-8139.
[30] 刘川,黄晓锋,兰紫娟,等.深圳市机动车PM2.5排放因子隧道测试研究[J].环境科学与技术,2012,35(12):150-153.
ACFDsimulationoftheeffectofstreetcanyonconfigurationsandwinddircetiononfineparticulatemattersdispersion
LIUJianfeng,WANGBaoqing,NIUHonghong,LIUBowei,RENZihui,CHENRonghui,WANGZebei.
(CollegeofEnvironmentalScienceandEngineering,NankaiUniversity,Tianjin300071)
The configurations of a real street canyon and wind directioon were considered to study their influence on the dispersion of fine particulate matters. The ratio of architecture height to street width (H/W) of street canyon,the gaps between buildings (ratio of the gap between buildings to the total length of the street) and wind dircetion were discussed. Computational fluid dynamics (CFD) software was used to simulate the detailed flow,turbulence characteristics and fine particulate matters dispersion distribution in street canyon. The results indicated the maximum fine particulate matters dispersion concentration of street central line were 37.5,46.4 and 28.4 μg/m3for the site of street central line of -19.3,-88.0 and -19.3 m (at the distance from the center of the street,the positive value indicated east of the street center,while the negative value indicated west of the street center,and the same below),respectively when the gap between buildings was 20%,wind direction was north,wind speed was 3 m/s andH/Wwas 1∶2,1∶1 and 2∶1 at 1.5 m above ground. The maximum fine particulate matters dispersion concentration of street central line were 88.1,31.6 and 33.7 μg/m3for the site of street central line of 148.0, -92.3 and -186.7 m,respectively whenH/Wwas 1∶1,wind direction was north,wind speed was 3 m/s and the gaps between buildings were 0,20%,40% at 1.5 m above ground. The maximum fine particulate matters dispersion concentration of street central line were 10.6,11.2 and 16.0 μg/m3for the site of street central line of 165.3,58.0,1.5 m respectively,whenH/Wwas 1∶1,the gap between buildings was 20%,wind speed was 3 m/s and wind directions were west,north and southwest at 1.5 m above ground. These results suggested that street canyon configuration and wind direction should be taken into account in modeling fine particulate matters dispersion.
street canyon; fine particulate matters dispersion; CFD; configuration
10.15985/j.cnki.1001-3865.2017.04.005
2016-02-18)
刘建峰,女,1991年生,硕士研究生,主要从事空气环境污染模拟。#
。
*国家留学基金委员会访问学者基金资助项目(No.201406205010);环保公益性行业科研专项(No.201009032);国家重大科学仪器专项(No.2011YQ060111)。

