基于协作相容性的工作流任务分配优化方法
胡海洋 姬朝配 胡 华,2 葛季栋
1(杭州电子科技大学计算机学院 杭州 310018)
2(复杂系统建模与仿真教育部重点实验室(杭州电子科技大学) 杭州 310018)
3 (计算机软件新技术国家重点实验室(南京大学) 南京 210046)
(huhaiyang@hdu.edu.cn)
在工作流调度中,各任务由工作流引擎调度系统中的资源来操作完成.由于不同的任务分配策略将对工作流管理系统的性能有很大的影响[1],因此需要制定良好的任务分配优化策略,将各任务分配给合适的资源.根据应用领域的不同,工作流系统中的资源可以是人力资源、设备仪器资源、应用程序或网络资源等.其中人力资源在工作流系统中起着重要的作用,他们一般是指具有特定技能的任务执行者,通过相应的角色(role)彼此配合与协作,在工作流系统中调度各类计算资源完成任务.在现代企业中,任务执行者常可承担多类角色用于完成多种任务[2],其对完成不同类型任务常可具有不同的熟悉程度,并且不同人员之间配合协作的默契程度也存在着差异.
任务执行者完成任务的技能熟悉度、彼此间协作的默契度对整个业务过程顺利、高效执行起着重要作用.然而,现有的任务分配算法仅考虑候选执行者的专业能力、兴趣、经验、负载等,忽略了工作流中任务交互时执行者之间的协作相容性.这样的协作相容性可以定义为:“和其他人的凝聚力、熟悉度,和谐、配合度等[2]”.例如一个典型的医疗索赔流程(如第2节中的图1所示),几个任务以确定的顺序分配给几个角色执行.当一个角色完成分配的任务并提交给下一个任务的执行者执行时,2个执行者之间可能会存在一些交互以询问和验证一些信息.在这样的任务交互过程中,执行者之间的协作相容性影响着工作的高效性.例如有2个员工甲、乙均可完成某个任务,并且甲的个人能力强于乙,然而甲对公司里其他员工的配合并不默契,当工作流中的任务需要员工之间进行交互时,甲的整体工作效率可能反而低于乙的整体效率.
此外,在工作流系统实际过程中,由于存在着多个流程实例,并且各实例到达时间有一定的随机性,候选执行者的工作列表中常存在多个等待处理的任务.在此情形下,一个满负载的执行者很难及时完成所分配的工作流任务.由于执行者当前所有的任务负载情况将对分配任务的最后完成时间有着很大的影响,因此工作流系统在分配任务过程中需考虑到各个任务执行者当前的工作负载情况,即尽可能将任务分配给轻负载(light-loaded)的执行者,从而提高整个工作流系统的性能.
现有的一部分研究工作通过将任务执行者的专业能力、任务成功率、兴趣度、经验等因素转化为模糊数[3-5],并对各影响因素分配一个权重因子,在任务分配时选择综合分数最高的候选者进行分配,但没有认识到任务间存在交互的情形下执行者之间协作的配合度影响.而有些研究尽管考虑了任务分配时上下文环境中任务执行者的一些社会关系、配合度等对任务执行时间的影响[6-9],然而却仅局限于连续的2个任务之间的配合度,同时也没有考虑到多实例同时到达的情况下任务执行者工作负载方面的影响.
为了解决以上问题,本文引入了执行者间协作相容性对任务分配影响的内容,通过结合历史日志的信息,对执行者间的协作相容性及任务负载进行了分析计算.在此基础上,给出了任务分配问题的优化建模,提出了基于协作相容性与负载均衡的任务分配算法,提高了整个流程实例的执行效率.
1 相关工作
在工作流调度中基本上任务分配策略是基于角色或组织模型[1].它仅仅考虑了资源的角色而没有区分自动型任务和用户型任务.研究者们通过人的属性扩展了这一概念,例如文献[2]基于流程任务间可能存在的交互,通过一个启发式算法,在任务分配时选择整个实例中合作协作相容性之和最大的执行者执行任务.文献[3]提出了一种多准则评估模型算法,根据候选者的能力、社会关系和任务属性进行任务分配,但对社会关系如何影响候选者的能力问题没有说明.文献[4]中提出了一种自主工作流任务分配策略,为任务分配带来了更多的自主权.
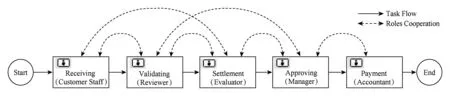
Fig. 1 A process flow of medical insurance claim图1 一个医疗保险索赔流程
文献[5]在研究任务分配时考虑了更多因素(如任务重要性、任务类型、能力、负载、经验),并用模糊理论讨论了关于每一因素权重的大小表示该因素的影响程度;文献[6-7]证明了基于优化社会关系的任务团队组建,如团队的凝聚力等,将使工作流中的任务更加高效地执行;文献[8]提出了一种基于社会关系矩阵处理多实例的任务分配问题;文献[9]采用隐Markov建模,通过基于候选者任务执行能力和日志中挖掘的连续任务的交互关系,并通过Viterbi算法解决任务分配问题;文献[10]提出了一种基于Q学习的任务分配算法,且在任务分配时考虑了社会关系的影响,缩短了实例的平均执行时间.然而,以上5种方法考虑的社会关系仅仅局限于连续任务的前置执行者,忽略了工作流中非连续任务之间存在交互时社会关系的影响,也未能充分考虑到执行者间的负载均衡.
此外文献[11]在任务分配时不仅考虑到当前待分配任务的候选者,也考虑整个实例执行中合作候选者间的依赖关系,优先选择历史合作次数最多的执行者.然而,他们都没有考虑到候选者的负载情况.文献[12]在任务分配时不仅考虑了任务候选者的个体属性,而且考虑了工作流中前一任务执行者对当前候选者的影响,改进了传统的最短处理时间、最短完成时间、平均工作负载和最短工作列表这4种任务分配算法,但同样没有充分考虑到工作流任务分配中的执行者工作负载均衡问题.文献[13-15]提出的动态任务分配策略,主要考虑了众包(crowdsourcing)执行环境中任务执行候选者在任务分配时的当前状况,具有一定的现实意义.文献[16]将机器学习算法用于工作流事件日志,在任务执行时根据算法生成的分类器推荐一个合适的执行者,以半自动的方法减少手动员工分配.文献[17-19]提供了解决任务分配问题的一个基本框架,但忽略了任务候选者之间社会关系的影响,也没有考虑到同时到达多实例时的情形.
综上所述,在任务分配时大多数的任务分配算法仅考虑候选执行者的个体能力属性,没有认识到工作流中不同任务交互时执行者之间的协作相容性对流程性能的影响.本文提出的基于协作相容性的任务均衡分配算法,不仅考虑了执行者当前的工作负载,而且考虑了流程实例运行中任务交互时候选者之间的协作相容性,更好地体现了工作流系统的实际运行情况.
2 基于协作相容性的任务均衡分配模型
2.1 问题描述和基本框架
本文通过一个具体实例来阐释相关问题.如图1所示的一个医疗保险索赔流程[2],该工作流程涉及索赔的受理(receiving)、材料的验证(validating)、理算(settlement)、审批签字(approving)和付款(payment)等任务处理过程,每个任务由不同角色执行的同时又有不同的交互.
该流程运行时,1)客服代表(customer staff)对医疗保险索赔进行记录并将由审查人员(reviewer)进行理赔调查或体检;2)评估人员(evaluator)根据审查人员所提供的信息进行索赔理算(settlement);3)经理(manager)对收到的赔偿款项进行签字确认;4)财务人员(accountant)将相应款项转入客户账户.
由于每一任务的角色可能处于不同的物理位置,使得任务执行过程中协作相容性的需求较大.在图1中,各任务上面的圆弧状虚线,表示执行不同任务的角色可能需要进行信息的交互.例如,收到索赔后,审查员可能需要客户服务代表澄清关于某些缺失的索赔信息(如发生事故的确切位置或事件的时间丢失).同样,评估员可能需要咨询审查员关于事故信息的更多细节.最后,财务会计人员可能会在付款之前咨询审查员说明一些支付选项不明的信息(如签字无效等).
因此,这里我们考虑的任务分配问题的场景如下:1)我们要考虑候选任务执行者的任务负载情况,即在分配时优选相对轻载的执行者;2)由于整个实例中不同任务可能存在交互的情况,不同执行者合作时所需的时间开销不同,因此任务分配时还需考虑执行者之间的协作相容性.任务执行者之间的协作相容性越高,交互时所需的时间越少.由于执行者可具备多种角色,即具有执行多种任务的能力,若任务分配时仅考虑优化协作相容性(我们假设一个执行者与自身的协作相容度最大),会导致多个任务分配给同一个执行者,这样大大增加该执行者的工作负载,因此,这2个优化目标之间存在一定的冲突.为了解决这个问题,我们提出了一个基于协作相容性的任务均衡分配基本框架(如图2所示).
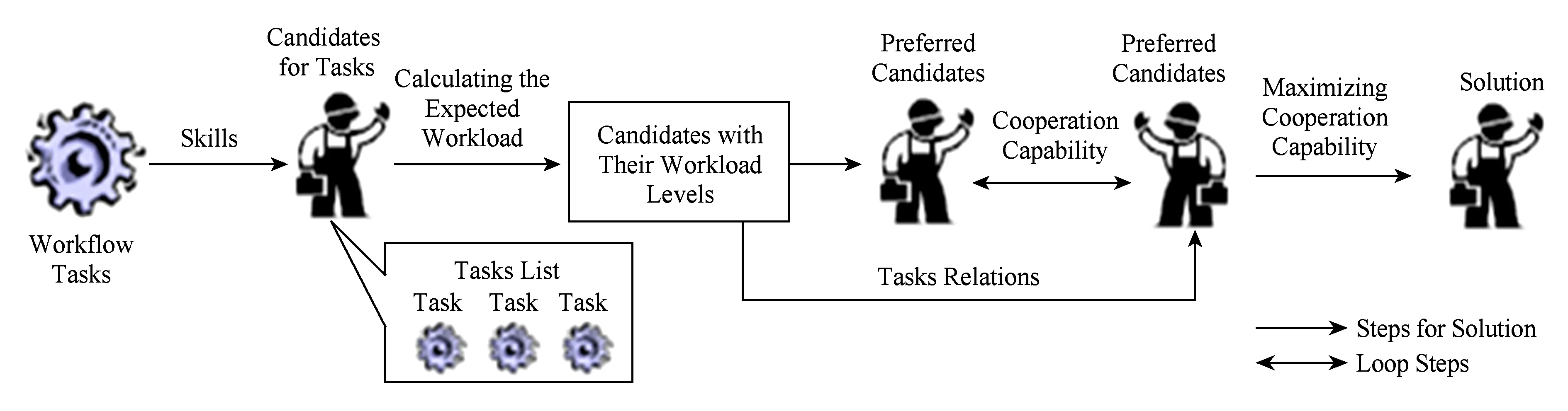
Fig. 2 Framework for tasks allocation based on cooperation capability图2 基于协作相容性的任务均衡分配基本框架
基于该框架,任务分配的确定过程如下:
1) 根据任务候选执行者之间相对预测负载大小(相关定义在2.2节中给出),将候选执行者划分为轻负载、中负载和重负载3个区间.同一区间内的候选者具有相似的负载.而在具体应用中,对候选者的相对预测负载区间数量和参数的设置,可根据工作环境的实际状况进行灵活调整;
2) 选择轻载区间内的候选者作为待分配任务的新候选者集合;
3) 根据具体任务之间的交互情形,从每一个任务的新候选者集合中,选择一个具有能力执行该任务且同时能最大化交互任务中执行者之间的协作相容性.
在工作流任务分配过程中,本文所做4点假设:
1) 工作流中所有任务候选者之间的协作相容性独立于具体的任务,且执行者之间的协作相容性具有对称性.
2) 执行者间的协作相容性与交互时所需时间成正比,即2个任务执行者间的协作相容性越好,任务执行时交流信息花费的时间越小.
3) 工作流运行过程中执行者总负载包括2部分:任务执行负载、与其他执行者交互所需的负载.其中,任务执行负载是当前预分配任务及执行者的工作列表中所有等待执行任务的负载.
4) 执行者对其工作列表中的任务进行处理时采用“先进先出”方式.
2.2 最优任务分配模型
根据图2中的基本框架,本节将给出具体的计算模型;为了方便描述和分析,表1给出了本文所使用的一些基本符号与定义.
我们用执行者完成其工作队列中所有任务所需的时间来表示他的工作负载.
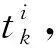
定义2. 设执行者uk当前负载为wcur(uk),若任务Ti即将分配给他,则uk的预测负载为
定义3. 设待分配的任务Ti的候选执行者集合为CEi={uk},且执行uk的预测负载为wpred(uk),则将候选执行者的负载进行归一化处理后可得到uk的相对预测负载为
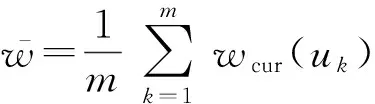
(1)
令Aik标识任务Ti是否被分配给执行者uk,cpij标识任务Ti与Tj需要交互,则工作流任务分配时执行者间发生交互时的总协作相容度可表示为
(2)
我们的目标是在分析执行者任务负载均衡的基础上,进一步通过使待分配任务的执行者与流程中各交互任务的执行者之间总体协作相容性最大,从而提高系统运行的效率.该任务分配问题可以描述成一个多目标整数线性规划问题:
max(CW,WL-1),
Aik≤Xik,1≤i≤n,1≤k≤m,
Xik∈0,1,1≤i≤n,1≤k≤m,
(3)
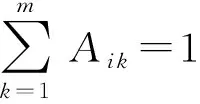
尽管式(3)是一个整数的线性规划问题,可以使用数学优化工具(如CPLEX)计算得出最优的分配方法,然而由于问题的规模,这是非常耗时的.因此,在后面我们首先给出计算执行者间协作相容性的方法,然后提出贪心算法,求解任务分配过程的局部最优解.
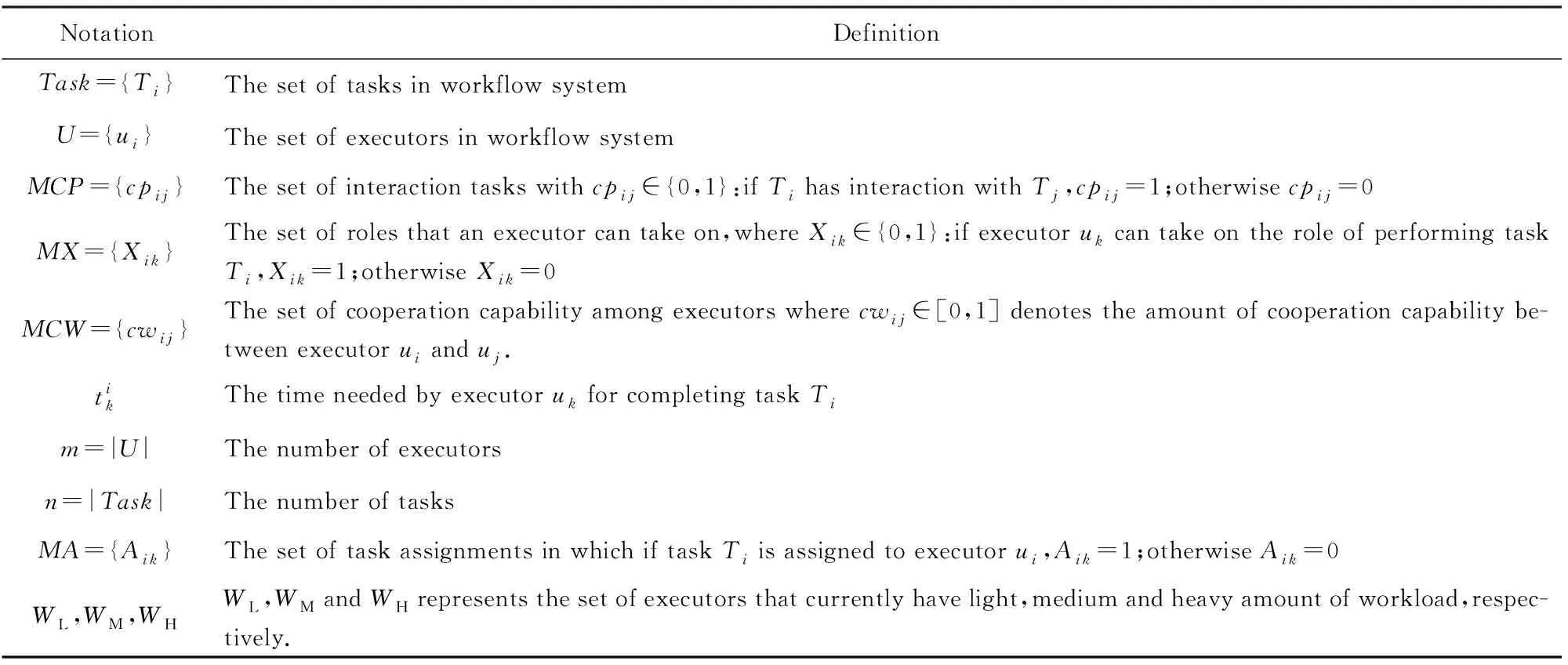
Table 1 Definitions of Notations表1 相关符号与定义
2.3 执行者间协作相容性
当工作流中的任务之间需要交互时,任务执行者间的高协作相容性可以加快他们信息的交流,提高任务执行的速度.一些电子商务网站如Epinions.com,Slashdot.org等通过询问用户记录成员之间的协作相容性来建立员工之间的信任网络或黑名单.然而,由于员工之间的协作相容性属于个人隐私,从而使得这种通过访问的方式来记录彼此间的协作相容性是非常不合适的.
根据任务执行者合作的多样性,本文主要通过工作流日志里执行者间协作完成流程的时间来度量他们的协作相容性,主要思想如下:对于发生交互的任意2个任务,计算进行协作的2个执行者之间平均吞吐时间与最小执行时间的差值,相对于2个任务中最多与最少的执行时间的差值比值,则该比值越小,协作相容性越大.协作相容性计算为
(4)
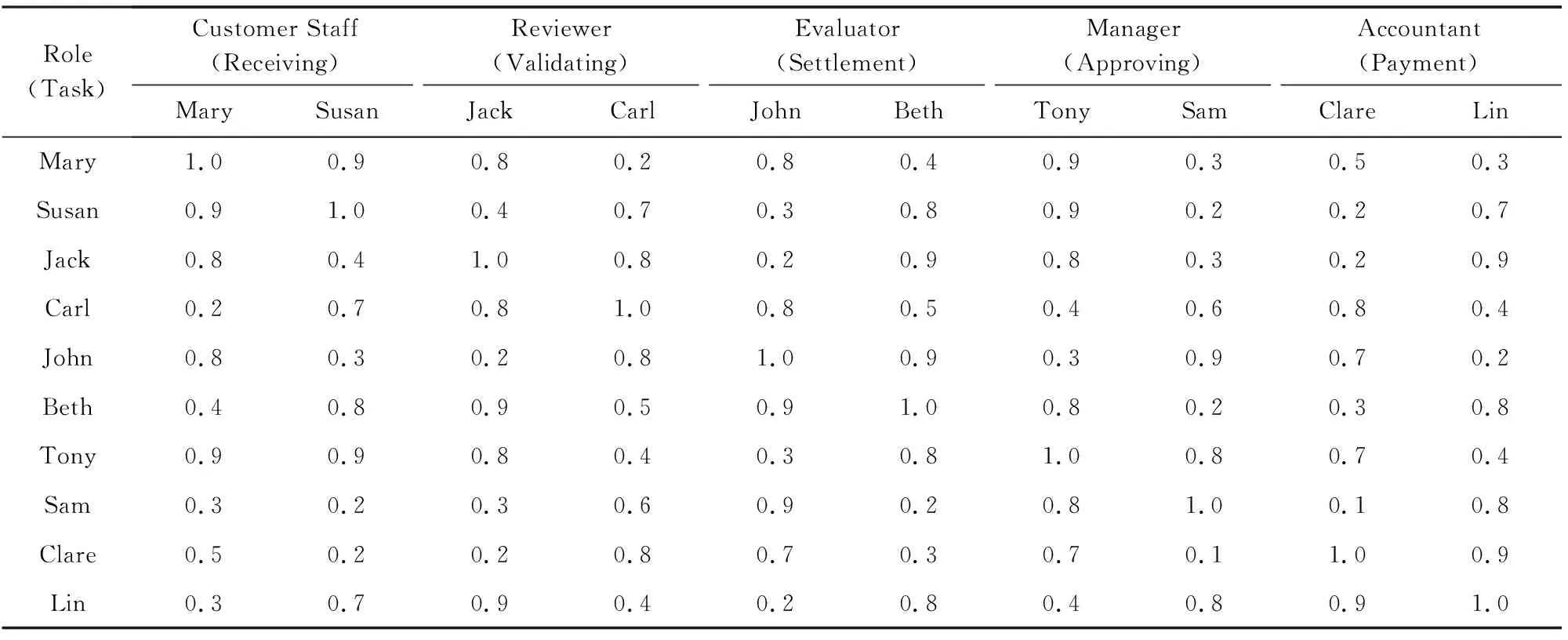
其中,cwkv表示uk,uv的协作相容性;tavg表示uk,uv配合时执行流程的平均吞吐时间;tmin表示流程的最小完成时间;tmax表示流程的最大完成时间;0<ω<1.显然,由式(4)所得的任务执行者之间的协作相容性取值范围为cwkv∈[0,1].例如,假设基于图1的一个流程日志解析得到的部分执行信息如表2所示:
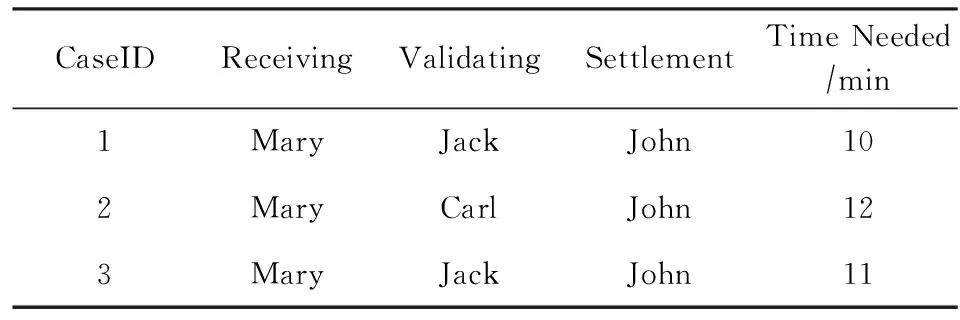
Table 2 Parts of Log Information表2 部分日志信息
由表2可得,流程的平均吞吐时间为tavg=(10+12+11)3=11 min,Mary和Jack配合时的流程平均完成时间为(10+11)2=10.5 min;流程的最大完成时间为12 min,最小完成时间为10 min;取ω=0.8,根据式(4)得:Mary和和Jack的协作相容性为0.8.同理可得,Mary和Carl的协作相容性为0.2.
3 任务分配策略
为了阐述本文所给算法的适用场合和相关特点,我们首先给出3种单目标的贪心算法,分别针对候选执行者的期望任务负载(expected workload)最小化、流程中所有任务完成的期望完成时间(expected completed time)最短以及基于预测负载的协作相容性最大化;然后在此基础上提出了联合优化执行者负载均衡及执行者间协作相容性的相关算法.在后面的实验中,我们将从不同的角度分析对比这4种算法.
3.1 期望任务负载最小化策略
下面给出期望工作负载最小化算法ESWL的执行过程:
算法1. ESWL算法.
输入: 执行者角色集合MX={Xik};
输出: 任务分配策略集MA={Aik}.
①MA=∅;
② FOR each taskTi∈TaskDO
③exp_workload=MAX_INT;k=0;
战时生活书店出版发行的文学期刊中有不少关于马列论文艺的重要论文,其观点精辟,为随后社会主义文学的发展有着重要的指导意义。这些论文大多集中在《文阵》上刊发,可概括为以下两大类。
④ FOR eachuj∈UDO
⑤ IF(Xij=1)
⑥ 计算uj的期望任务数λj;
⑦ IF(λj ⑧exp_workloadλj; ⑨kj; ⑩ END IF ESWL算法对流程中的每一个待分配任务,需要遍历所有的候选者,因此,其时间复杂度为O(mn),其中n是流程中任务的个数,m是所有执行者数. 对于流程的期望完成时间最短算法ESCT,其主要思想是:在任务分配时,遍历所有具有执行该任务能力的候选者,考察当前的执行者完成及其所携带的工作列表,计算新任务完成的期望时间,期望时间最短的执行者将被挑选出,并将该任务分配给它.由于执行者uk可承担的任务集为Taskk={Ti|Xik=1,i=1,2,…,n},则uk完成任务的平均时间为 若uk当前待完成的任务集为TAk,考虑到当uk完成TAk中任务时系统还会分配新任务,则uk完成任务的期望时间为 下面给出期望完成时间最短化算法ESCT的执行过程: 算法2. ESCT算法. 输入: 执行者角色集合MX={Xik}; 输出:任务分配策略集MA={Aik}. ①MA=∅; ② FOR each taskTi∈TaskDO ③ FOR eachuj∈UDO ④exp_time=MAX_INT;k=0; ⑤ IF(Xij=1) ⑥ 计算uj完成任务的期望时间γj; ⑦ IF(γj ⑧exp_timeγj;kj; ⑨ END IF ⑩ END IF 同样地,该算法对流程中的每一个任务,也需遍历所有的候选者.因此,时间复杂度为O(nm),其中n是流程中任务的个数,m是所有候选者的个数. 我们首先根据式(4)计算出执行者之间的协作相容性;然后在文献[2]的基础上,给出协作相容性最大化算法MCW的主要步骤如下:在任务分配时,遍历所有具有执行该任务能力的候选者,考察当前的执行者与所有交互任务的执行者协作相容性,从中选择协作相容性最大的执行者分配该任务. 下面给出协作相容性最大化算法MCW的算法伪码: 算法3. MCW算法. 输入: 执行者角色集合MX={Xik}、任务交互集合MCP={cpij}、执行者协作相容集合MCW={cwkv}; 输出: 任务分配策略集MA={Aik}. ① FOR eachuk∈UDO ② FOR eachuv∈UDO ③ 由式(4)计算uk与uv间协作相容性cwkv的值; ④ END FOR ⑤ END FOR ⑥ FOR eachTi∈TaskDO ⑦max_coop0;v0; ⑧ FOR eachukDO ⑨ IF(Xik=1) ⑩max_coop[k]0; 如上所述,该算法对流程中的每一待分配任务,需要遍历所有的候选者及任务集合,用以找到与所有交互任务执行者之间的协作相容性.因此,时间复杂度是O(mn2). 我们将考虑在执行者负载相对均衡的基础上,且使得执行者间整体协作相容性最优的任务分配算法.在设计这样的分配算法MCLB时,需要考虑到流程中存在任务交互的情形,因此,算法需要3个输入集合:任务交互集合MCP={cpij}、执行者协作相容集合MCW={cwkv}及执行者角色集合MX={Xik}.在任务分配过程中,我们目标是在保持执行者间工作负载相对均衡的基础上,最大化整个流程中交互任务间的执行者协作相容性.为了实现这个目标,我们首先通过一个映射函数,将执行者之间的协作相容性值映射为任务交互时花费的时间,即对2个执行者而言,若他们的协作相容性越高,则彼此交互所需的时间越少.设2个执行者uk和uv分别执行任务Ti和Tj,他们之间协作相容性为cwkv,则他们交互时间开销可表示为 (5) 其中,β是协作相容性对时间映射的比例因子.对于任一执行者uk,若考虑将任务Ti分配给他,则任务Ti完成的预测时间为 wpred(uk)=wpred(uk)+ (6) 由于在任务分配过程中,当分配Ti时,可能存在着其他任务尚未被分配给任何执行者,因此,利用式(6)计算Ti分配策略时,我们仅考虑Ti与那些已分配好执行者的任务间的交互情形. 下面给出面向负载均衡的、最大化整体协作相容性的任务分配算法MCLB伪码: 算法4. MCLB算法. 输入: 执行者角色集合MX={Xik}、任务交互集合MCP={cpij}、执行者协作相容集合MCW={cwkv}; 输出: 任务分配策略集MA={Aik}. ① FOR eachuj∈UDO ③ END FOR ⑤ IF(!IsExistCoop(MCP))*判断是工作流程是否需要任务交互* ⑥ FORTi∈TaskDO ⑦ 利用ESWL算法找出当前期望负载最小的后续执行者uk; ⑧Aik1; ⑨ END FOR; ⑩ ELSE 函数IsExistCoop(MCP)判断输入的流程中是否存在任务交互.若流程中不存在任务交互时,时间复杂度为O(nm);当任务间存在交互时,该算法在任务分配时,对每一待分配任务,在遍历相对轻载的候选者集合时,还需在该可能候选者的基础上遍历其他所有可能交互的任务.因此,算法的时间复杂度是O(m2n2),其中n是任务的个数,m是所有候选者的个数. 为了便于阐述上述方法,现给出了基于图1场景的一个简单例子.假设图1中每一任务的角色、执行者如表3所示: Table 3 Task Roles and Candidates表3 任务角色及候选者信息 其中,基于图1的任务交互矩阵如表4所示: Table 4 Matrix of Task Interaction表4 任务交互矩阵 设执行者之间计算所得的协作相容性矩阵为表5所示: Table 5 Matrix of Cooperation Capability表5 协作相容性矩阵 基于上面前提条件,则在运行时有如下情形: 1) 初始时所有候选者的工作列表为空,即任务候选者的待执行任务的负载为0;当到达第1个流程实例时,流程中所有任务的待候选者均为空闲(即都在轻载集合中).这时,通过最优分配模型,得到总体最大化协作相容性的任务分配情况如下:{receiving:Mary,validating:Jack,settlement:Beth,approving:Tony,payment:Clare}.总体协作相容性为:4.4. 2) 假设在某一时刻新的流程实例到达时,所有任务的候选者工作列表中都有等待完成的任务,即一定的工作负载,且通过估算执行者的预测负载及相对预测负载值,划分的新候选集合如下:WL={Mary,Susan,Carl,Clare,Lin};WM={John,Beth,Tony};WH={Jack,Sam}. 在任务分配时,首选我们考虑的是负载,将对应的轻载集合作为新任务的候选执行者集合.因此,首先从WL集合中搜索具备执行该任务角色的候选者,直到对应轻载集合搜索完为止,若未发现具备承担该任务角色的执行者,再依次搜索WM与WH.例如在分配任务receiving时,由于该任务的2个候选执行者均在WL集合中,因此,候选执行者集合就为WL中的Mary,Susan.而在搜索任务validating的候选者集合时,WL中有一个可能的候选者Carl,则任务validating的候选执行者集{Carl}.通过以上候选执行者集合的确定,然后针对分配的可能情况,选择任务交互时执行者间协作相容性最大的进行相应分配,结果如下:{receiving;Susan,validating:Carl,settlement:Beth,approving:Tony,payment:Clare},总体协作相容性为3.9. 本节对ESWL,ESCT,MCW,MCLB这4种算法进行实验比较来分析各个方法的特点与性能.仿真采用的工作流顺序模型如图3所示: Fig. 3 Workflow model图3 工作流模型 在实验中,我们根据相对预测负载值设置轻负载、中负载、重负载区间,即WL=[0,0.34),WM=[0.34,0.67),WH=[0.67,1).首先使用ESWL算法,产生相应的工作流日志.根据所产生的工作流日志信息,计算任务执行者之间的协作相容性和执行者任务平均完成时间,将协作相容性值存入协作相容性矩阵;在工作流实例不同到达概率的情况下,使用不同的任务分配算法和相应能力配置进行仿真实验.对每一实例到达的概率,使用每种算法进行100次的仿真,并使用相同的实例队列和迭代次数在其他算法进行仿真,采取平均100次的仿真结果作为最终的结果进行分析.实验中工作流实例到达的概率服从二项分布. 各任务的处理时间设置如表6所示.在实验中,执行者可承担的角色设置为2种情况:任务执行者仅具备单一角色、任务执行者可具备多个角色的情况(如表7、表8所示);流程中任务间的交互情形又分为2种情况:任务间存在交互、任务间不存在任何交互(如表9、表10所示).通过结合执行者能力、负载以及任务交互的特点,仿真实验了所有4种可能情况下的结果. Table 6 Processing Time of Tasks Table 7 Each Executor Has a Single Role表7 任务执行者仅具备单一角色 Table 8 Each Executor Can Have Several Roles表8 任务执行者可具备多个角色 Table 9 Tasks Have No Interactions表9 任务间无交互情形 Table 10 Tasks Have Interactions表10 任务间存在交互情形 任务无交互情况下是在表7和表8配置下,结合表9进行仿真实验.实验结果如图4所示.通过观察图4(a)可以看出,4种算法下工作流实例完成时间几乎相同.这是由于在一个任务执行者仅具备单一角色且无任务交互时,其他3种算法的本质上是一样的,都是基于最小负载进行任务分配的,能够达到任务的均衡分配.MCW算法的任务执行者是随机分配的,没有考虑候选执行者实际的负载情形.通过观察图4(b),MCLB算法和ESCT算法完成时间几乎相同,ESWL和MCW算法略差且具有交叉性.这是由于在一个任务执行者可具备多个角色下,ESWL算法仅以期望任务负载作为任务分配的立足点,并不能正确地反映候选者的实际任务负载.仿真的结果表明,在没有任务交互的情况下,MCLB算法仍然取得了较好的性能. Fig. 4 Completed time of workflow instances with no task interactions图4 无任务交互情况下工作流实例的完成时间 我们现在考虑在工作流实例中任务有交互情况下,实验结果如图5所示.通过观察图5可以看出,在2种场景下,MCLB算法的结果都是最好的,MCW算法最差.这是由于存在任务交互时,MCLB算法不仅考虑了任务的负载,还考虑了交互任务执行者的协作相容性,一定程度上缩短了任务交互时的花费时间.而ESCT算法仅考虑了期望完成时间,ESWL算法仅仅考虑期望任务负载.尽管MCW算法考虑了任务候选者与前置所有任务候选者的协作相容性,但却忽略了多实例同时到达的场景,也即忽略了任务负载的影响.同时,从图5(a)和图5(b)的结果对比中可以发现,MCLB算法在后一种场景下的效果,要比前一种场景下的优势更大,这是由于实验中任务候选者增多时任务选择性变得更多. Fig. 5 Completed time of workflow instances having task interactions图5 存在任务交互情况下工作流实例的完成时间 下面我们考察任务执行者之间的协作相容性对工作流实例处理时间的影响.当工作流实例中的各任务间无交互情形时,4种任务分配算法中工作流实例的平均处理时间总是大小相等,即约为54 min;而当工作流任务存在交互情形时(如图6所示),4种任务分配算法的执行时间是不同的.使用MCW算法和MCLB算法时,工作流实例的平均处理时间总是优于其他2种算法.其中,图6(a)中,MCLB算法下工作流实例的平均处理时间比ESCT算法约少2 min,比ESWL算法约少3 min.图6(b)中,MCLB算法比ESCT算法约少2.5 min,比ESWL算法约少1.3 min.相比之下,MCW算法比ESCT算法约少5 min,比ESWL算法约少6 min.MCW算法下的平均处理时间最小的原因在于,它总是能够使当前任务执行者的协作相容性最大,尤其在任务执行者具备多个角色时,会将连续的多个交互任务分配给同一执行者.同时,通过将图6(a)和图6(b)的结果对比可以发现,在任务执行者可具备多个角色的情况下,使用ESCT算法得到的效率比ESWL算法要差.这是由于ESCT算法不能根据一个任务执行者可具备多个角色这一特点进行灵活地分配,造成前面任务候选者的选择严重影响后面其他任务的候选者选择情况. 我们现在分析在4种任务分配算法下任务执行者的负载均衡,其中执行者的总负载为所分配任务的总执行时间加上实际运行中交互时的花费时间.图7中给出了相关的实验结果.从图7(a)结果可以看出,当任务执行者仅具备单一角色时,MCLB算法能够使任务所有候选者的总负载相对均衡,而其他3种算法下任务候选者的负载情况相差较大.例如任务T3的候选者u5,u6,MCLB算法下u5比u6多3.15%,ESWL算法下多13.26%,ESCT算法下多23.74%,而MCW算法下u5比u6少68.04%.从图7(b)结果可以看出,一个任务执行者可具备多个角色时,MCLB算法同样能够均衡全局任务执行者的负载,而其他3种算法下任务的执行者负载不能保持相对均衡.例如T4的所有候选者有u7,u8,T5的所有候选者有u8,u9,u10.尽管u8可以同时执行2个任务,但MCLB算法下2个任务所有候选执行者的负载相对于其他算法,仍然具有较好的均衡效果. Fig. 6 Average processing time of a workflow instance having task interactions图6 存在任务交互情形时工作流实例的平均处理时间 Fig. 7 Workload for each executor when 20 instances having task interactions arrived per hour图7 每小时到达20个实例时任务交互情况下执行者的工作负载 本文研究了基于协作相容性的工作流任务分配问题及算法.通过对工作流中任务之间的交互与否以及执行者之间的协作相容性对工作流性能的影响进行建模,并在考虑负载均衡的基础上,通过将交互任务的执行者协作相容性整体最大化以实现最终的任务分配,减少了流程实例的平均吞吐时间,提高了工作流的整体性能.通过实验得出,基于协作相容性的任务均衡分配方法对工作流中是否存在交互任务的情况均有良好的执行效率. 由于执行者之间协作相容性大小涉及的因素可能有很多,因此本文计算协作相容性的方法有待进一步细化.同时,由于具体的工作流流程有顺序、选择、并行结构,而本文只关注了顺序结构.因此,未来的研究包括3个方面:1)通过考虑更多的因素,进一步完善协作相容性的计算方法;2)考虑工作流中具有选择、并行结构时任务执行者间协作相容性的影响;3)考虑任务间存在转换概率时的协作相容性概率期望值.3.2 期望完成时间最短化策略
3.3 协作相容性最大化策略
3.4 联合优化策略
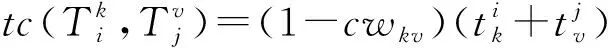
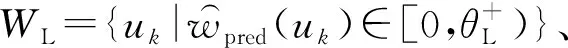
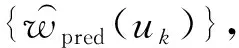
3.5 基于最优模型分配的一个例子
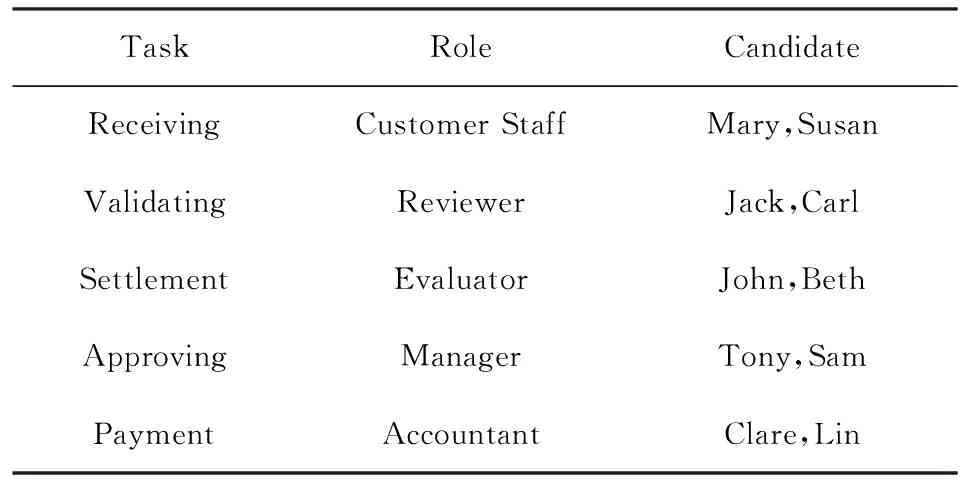
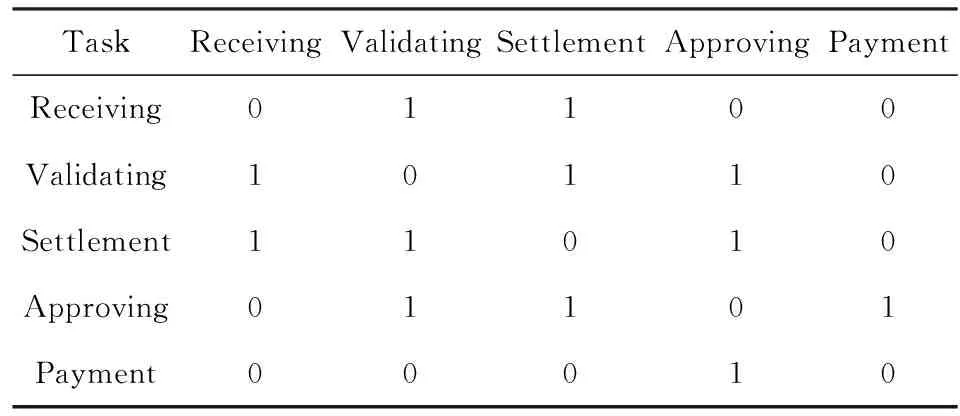
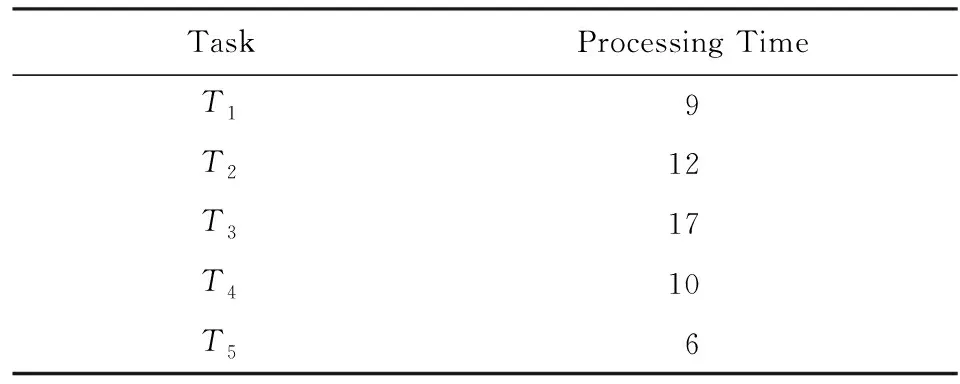
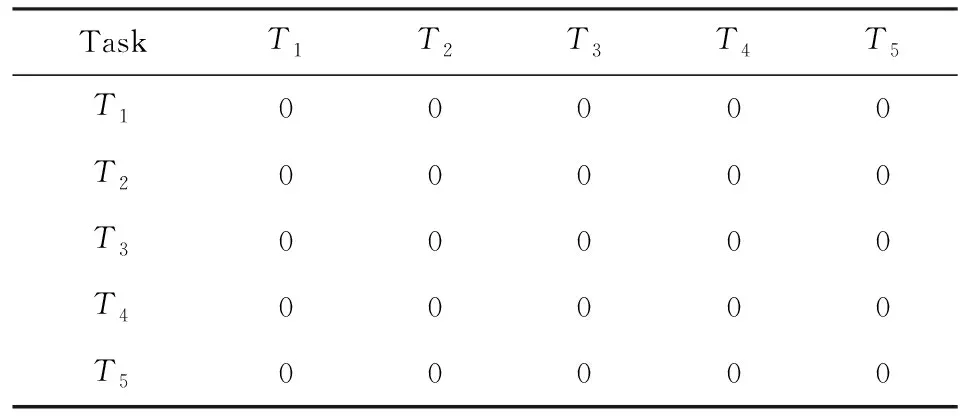
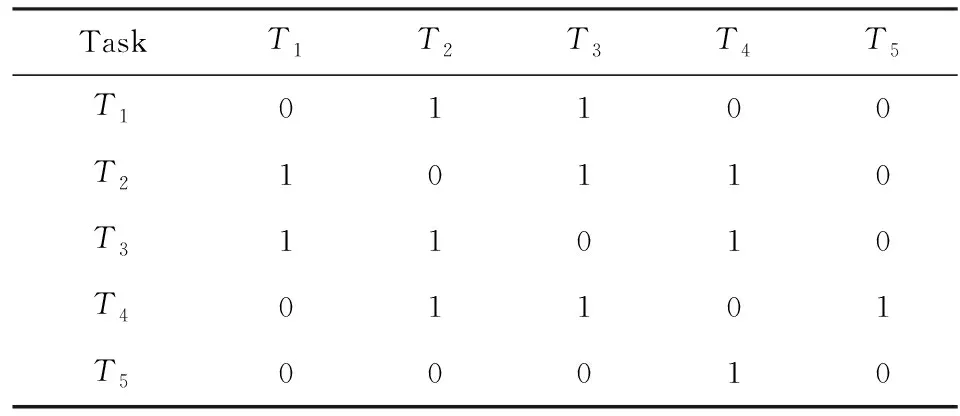
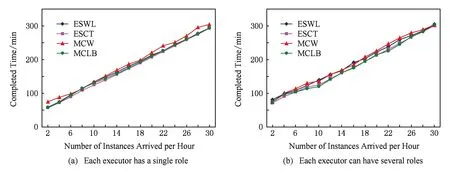
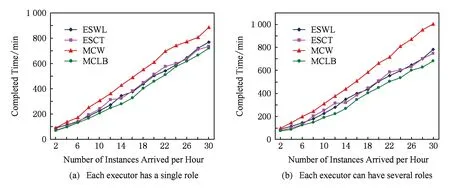
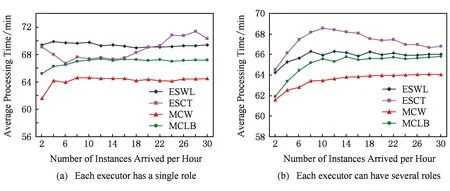
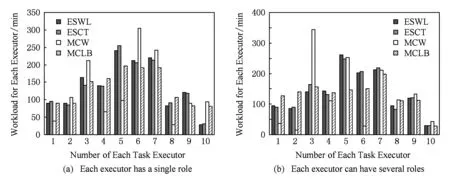
4 实 验



5 结 论

