能源互联网下基于储能调度及多源供能的数据中心能效优化
孙春蕾 温向明 路兆铭 盛万兴 曾 楠 李 洋
1(北京邮电大学信息与通信工程学院 北京 100876)
2(网络体系构建与融合北京市重点实验室(北京邮电大学) 北京 100876)
3(先进信息北京市实验室(北京邮电大学) 北京 100876)
4(中国电力科学研究院 北京 100192)
5 (国家电网公司 北京 100031)
(scl1992@bupt.edu.cn)
随着大数据、云计算及“互联网+”的发展.数据中心在数量与规模上面临着爆发式增长.同时,数据中心能耗问题日益成为社会关注的焦点.据统计,2013年美国本土数据中心能耗达到了91MWh[1],到2030年数据中心的耗电量有可能突破全国用电量的20%[2].因此,数据中心的能效优化问题变得尤为重要.目前,关于数据中心能效优化的论文主要包括2个方面:
1) 从提高电源系统本身的能源转换效率角度,例如文献[3]和文献[4].其中文献[3]从提高供电系统电压、电流转换效率的角度研究数据中心能效优化问题;文献[4]从电池本身的物理构造角度阐述充放电效率与循环寿命的问题.
2) 从数据中心业务负载均衡的角度,例如文献[5-7].其根据实时电价,对分布式数据中心间的业务分配进行负载均衡,对数据中心中处于开启状态的服务器数量进行优化,进而降低数据中心能源成本.
近年来,能源互联网的发展为数据中心能效优化问题提供了新的解决思路.首先,储能系统在削峰填谷及提高电源系统稳定性等方面的作用日益突出.其次,分布式清洁能源的发展以及售电侧的放开[8-10],为数据中心等高耗能用户提供了多源能源选择的可能性.因此如何在实时电价及多源供能的背景下,结合储能时序的优化,在降低数据中心能耗成本的同时,提高清洁能源占比是一个很有意义的问题.本文旨在从储能、多源能源供应的角度对数据中心的能源利用效率进行优化.本文的主要工作包括3点:
1) 引入污染指数函数,对不同清洁程度的能源进行惩罚,实现了对用户节能行为的激励,同时提高了清洁能源使用比例.对节能减排具有重要意义.
2) 通过构建储能操作成本以及未来潜在成本实现了对储能充放电电量的时序优化,一方面实现了削峰填谷,另一方面进一步降低了数据中心能源成本.
3) 构建了基于凸二次规划的数据中心能源成本模型,并针对相关问题的具体特点给出了求解算法.如算法1实现了不考虑储能时序优化时的能源成本最优解的求解.
1 数据中心能源系统建模
1.1 数据中心能源系统模型简介
数据中心的能源系统如图1所示,主要包括一个智能的能源控制器、标准配比的储能系统以及支持多源供应的电源系统.式(1)给出了数据中心能源系统的供需平衡关系.
(1)
其中,P(t)表示当前时刻数据中心的总能耗,o(t)表示当前时刻储能系统的充放电电量,qn(t)表示当前时刻第n种能源的购买量,且n∈N={1,2,…,N}.

Fig. 1 Block diagram of power system for data center图1 数据中心能源系统示意图
根据文献[11],数据中心的能耗主要包括IT设备、空调系统、电源、照明等几部分.其中,与业务信息传输相关的通信设备能耗、与业务服务相关的服务器能耗及与服务器散热制冷相关的空调系统能耗占数据中心整体能耗的80%~90%.式(2)定义了一台内核数为k、服务率为u、主频为f的服务器在业务到达率为λ时的基础功耗[7]:
(2)
其中,α≥3,ρ为服务器的利用率.
因此,数据中心的整体能耗如式(3)所示:
P(t)=θ1mac(t)Pserver(t)=θ1mac(t)kρfα,
(3)
其中,mac(t)为处于活跃状态的服务器数量,θ1为服务器基础功耗与数据中心整体功耗的比例.由文献[11]可知θ1≈5.
1.2 基于污染指数的多源能源选择模型
随着能源互联网的发展,清洁能源占比日益提高,地方上也日益涌现出不同规模的售电公司,打破了国家电网公司在售配电市场的垄断格局,为以数据中心为代表的高能耗用户提供了多源能源选择的基础.即用户可以根据电价、电能质量等指标自主地从一家或多家售电企业购买电能.本文在实时电价及多源能源选择的背景下引入污染指数的概念[12],对数据中心的能源选择及其成本进行建模.在降低数据中心能耗成本的同时,改善数据中心能源结构,提高清洁能源使用率.
为了促进清洁能源的使用,污染指数函数需要满足2个条件:1)随着买电量的增加,污染成本逐步增加;2)随着买电量的增加,污染边际成本逐渐增加.因此,我们定义污染指数函数如式(4)所示:
C(qn)=γn(qn)2+βnqn,γn,βn>0,
(4)
其中,qn为第n种能源的购买量;γn和βn为第n种源的污染系数.能源的清洁度越高,污染系数越小.
因此,当前时刻数据中心的买电成本如式(5)所示:
(5)
其中,pn为当前时刻第n种能源的电价.
1.3 基于预测电价的储能时序优化模型
根据文献[13-14],当前时刻储能充放电电量的优化,必须同时考虑2个因素:1)电池充放电时的能源损耗及电池的循环使用寿命,即储能的操作成本;2)当前时刻电池的充放电电量对未来时刻电池充放电电量的影响,即储能的潜在成本.比如,提高当前时刻储能系统的放电量,虽然可以减少当前时刻的能源购买成本,但是可能会造成未来时刻储能系统充电量的增加,进而增大未来时刻能源的购买成本.
基于以上2点,如式(6)所示,构建储能成本:
(6)

(7)

(8)
2 基于凸二次规划的数据中心能效优化模型
2.1 无储能情况下的能效优化问题
在不考虑储能时序优化的情况下,根据1.1节及1.2节,系统成本函数可表示为式(9).本文引入污染指数对每种能源的污染成本进行惩罚.一方面,在降低数据中心整体能源成本的同时,对其能源结构进行优化,提高清洁能源占比;另一方面,因为边际成本随着用电量的增加而增加,进一步促使用户节约能源,实现节能减排.

(9)
式(9)在无不等式约束下的拉格朗日对偶函数及其最优解表示如下[15-16],其中φ为拉格朗日因子:
(10)
(11)
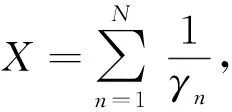
本文结合拉格朗日对偶法,提出了适应于式(9)的求解算法——算法1,并在数学上给出了解的最优性证明,具体证明细节见附录A.同时,本文在第4节给出该算法与内点法等数值仿真方法的性能比较.
算法1. 最优电量求解算法.
① 初始化相关参数及变量
② Repeat
③ 根据式(10)(11)求解拉格朗日对偶解;
④ 对拉格朗日对偶解进行修正

End If
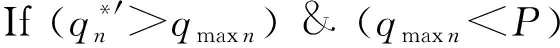
End If
⑤ 将经步骤④修正过的能源n剔除集合;

值得注意的是,绝大多数数据中心均配置一定规模的储能系统,且本文的重点也是对有储能配置的数据中心进行能效优化.研究不考虑储能时序调度下的数据中心能效优化问题的意义在于为2.2节中的储能策略提供对比基准.
2.2 有储能情况下的能效优化问题
根据第1.3节,在对有储能时的能源成本进行建模时,除了考虑储能对能源购买总量的影响外,还需要考虑储能自身的操作成本以及潜在成本.式(12)给出了当前时刻基于多源能源选择及储能时序优化的数据中心能源成本模型.
minC({qn},o,oH)=
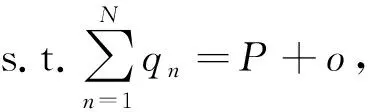
P=θ1mackρfα,
qmin n≤qn≤qmax n,
smin≤s0+o≤smax,
l=1,2,…,H,
其中,s表示储能系统中的电量;smin和smax分别表示储能系统中电量的下限和上限;s0表示当前时刻储能系统电量的初始值.
根据观察,式(12)的目标函数为二次幂函数,且约束条件均为线性约束.根据文献[17-18],式(12)为典型的凸二次规划问题,可通过内点法、SQP等典型凸二次规划算法求解.
3 实验与结果
本节将对本文提出的模型进行仿真分析.为了不失一般性,我们假设数据中心可以选择大电网、风能以及光伏3种不同的能源.其基础电价分别为0.55CNY,0.65CNY,0.90CNY;峰谷电价调节比例分别为50%,30%,30%.其污染指数分别为γ1=0.25P,β1=0.1;γ2=0.20P,β2=0.07;γ3=0.15P,β3=0.05.
3.1 多源能源选择仿真分析
图2描述了污染指数对单位购电成本的影响.对于一个1 MW的数据中心,随着购电量从0.1 MWh增加至1 MWh,其单位购电成本也从0.67元增加至0.79元.说明污染指数的引入可以通过增加高耗能用户的平均单位能源成本,加重对高耗能行为的惩罚,从而激励用户节约能源,实现节能减排.
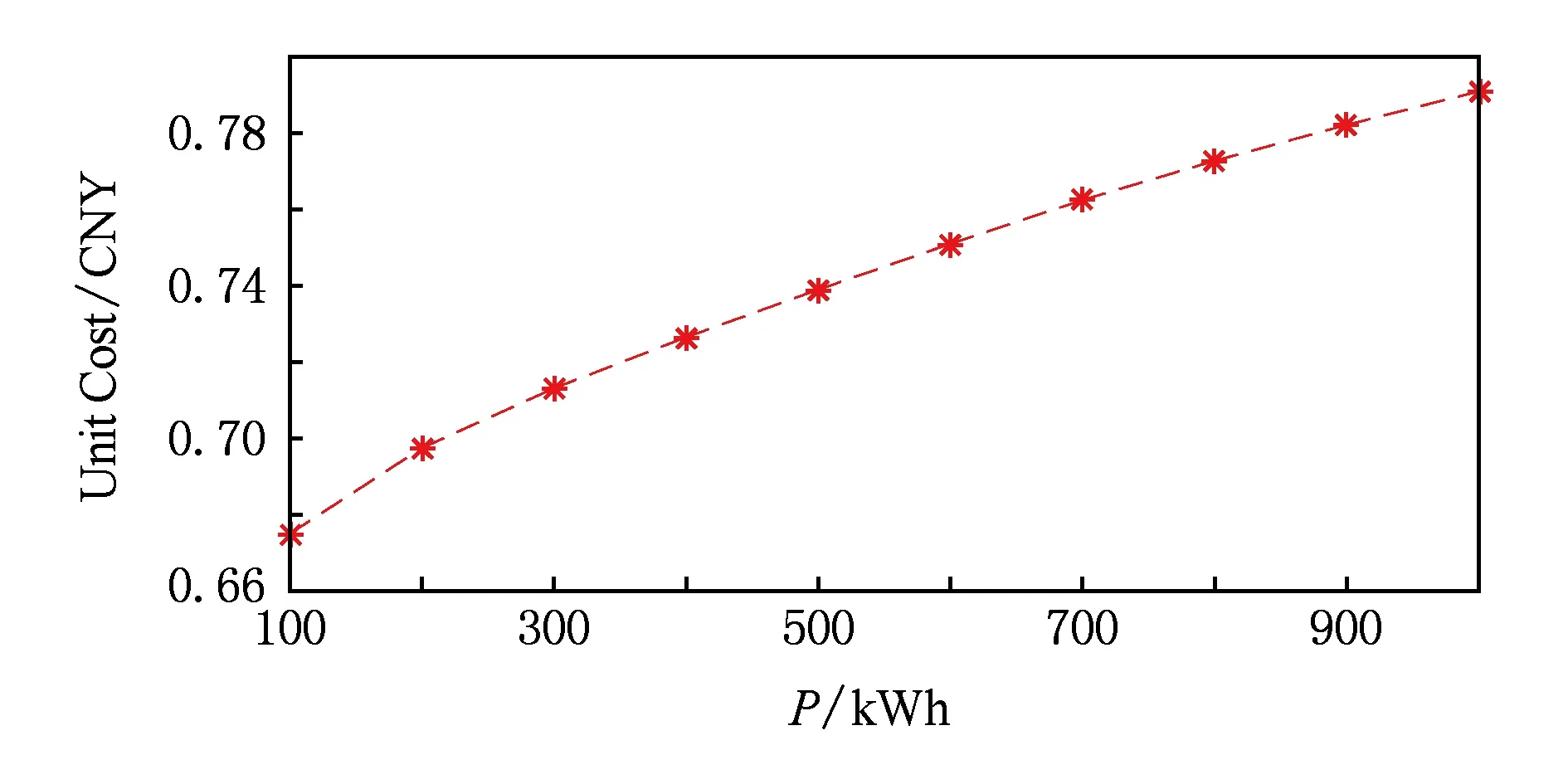
Fig. 2 Influence of pollution index on unit cost图2 污染指数对单位成本的影响
图3描述了全天0:00~24:00随着不同能源实时电价的变化,各种能源购买量在能源购买总量中的占比.分析得出污染指数的引入可以促进多种能源的协调利用,避免了因为电价低廉而购买单一能源的情况.尤其是削减了价格低廉的火力发电购买量,相对提高了价格较高但污染成本较低的清洁能源的使用量.

Fig. 3 Real-time price and purchase decision of each energy resource图3 实时电价及能源购买量
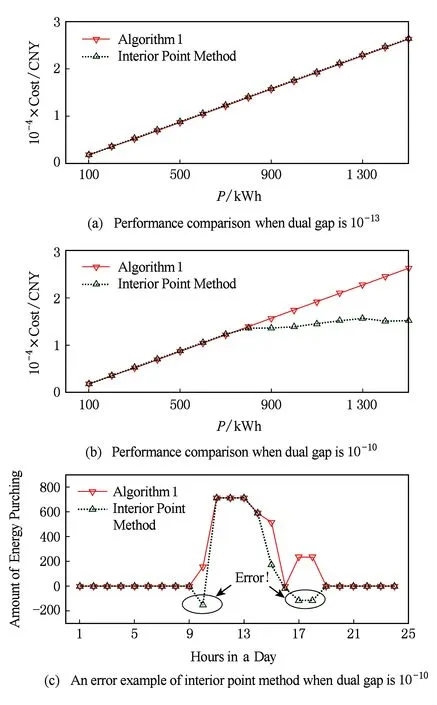
Fig. 4 Performance comparison of algorithm 1 and interior point method图4 算法1和内点法性能对比
图4描述了算法1和内点法的性能对比.当内点法的对偶间隙精度较高时,算法1与内点法所求解的精确度基本相同,但由表1可知,算法1的收敛速度大约是内点法的30倍.此外,随着内点法对偶间隙精度的降低,算法容易出现明显错误.图4(c)描述了对偶间隙精度为10-10时内点法的错误情况.

Table 1 Convergence Time of Algorithm 1 andInterior Point Method
3.2 有储能时能源成本仿真分析
图5描述了当前时刻储能充放电电量对未来时刻的影响,其中d(h)=‖oh(o=o′)-oh(o=200)‖.在1 MW的数据中心中,以当前充电量为200 kWh为参考,分别给出了当前时刻充电量变为100 kWh和400 kWh时储能系统未来时刻充放电电量的变化情况.由图5可知,当前时刻储能充放电电量对未来6~7个小时内的储能充放电情况影响比较明显.因此,仿真实验中取H≥6即可.

Fig. 5 Influence of present battery charging and discharging on that in future图5 当前时刻储能充放电电量对未来时刻的影响

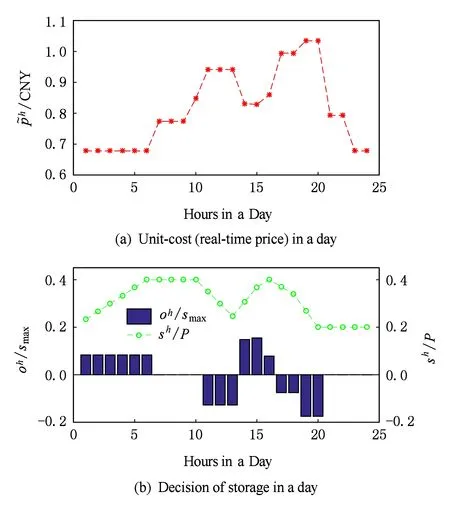
Fig. 6 Connection of battery charging and real-time price图6 储能充放电电量与实时电价的关系
图7描述了数据中心配置储能系统后,比未配置储能系统时实现的成本节约量.由图7可知,随着数据中心规模的增大以及储能配置容量的增加(从10%增加至40%),其节省的成本也随之增大.对于一个1.5 MW、储能配比为40%的数据中心,每年可节约高达10万元的能源成本.
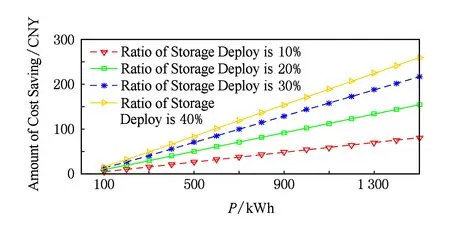
Fig. 7 Influence of storage on the economy of energy cost图7 储能对节约能源成本的影响
3.3 电价预测方法对能源成本的影响
在对储能的潜在成本进行建模时,涉及到对未来时刻单位能源成本的预测.图8描述了3种不同电价预测方法对能源成本节约量的影响.因为电价预测方法不是本文的重点,因此本文简单地采用下文中的3种方法进行实验仿真.结果表明,未来时刻单位能源成本预测的准确性对本文模型的性能有一定的影响.

Fig. 8 Comparison of profit by different price prediction methods图8 不同电价预测方法下能源成本节约量的对比
1) 方法1

2) 方法2
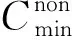

3) 方法3

其中,e为一个很小的常数.
4 总结与展望
本文主要从储能、多源能源供应的角度对数据中心的能源成本进行了优化.首先引入污染指数函数,对高耗能用户及不同清洁程度的能源进行惩罚,实现了对用户节能行为的激励,同时提高了清洁能源使用比例.其次,通过构建储能的操作成本以及未来潜在成本实现了对储能充放电电量的时序优化.一方面实现了削峰填谷,另一方面进一步降低了数据中心的能源成本.最后,构建了基于凸二次规划的数据中心能源成本模型,并针对相关问题的具体特点给出了求解算法.仿真结果表明:随着数据中心规模的增大以及储能配置容量的增加,通过运用本文提出的能源成本优化模型,其节省的成本越多.对于一个1.5 MW、储能配比为40%的数据中心,每年可节约高达10万元的能源成本.
本文仅仅从数据中心能源系统本身的角度对其能源成本进行了优化.业务QoS保障与能源成本的综合优化、数据中心的最佳储能配比、高效准确的电价预测方法等是未来的研究方向.

