科氏流量计测量管振动频率检测及跟踪方法研究
黄 磊
(中国石油大学胜利学院 机械与控制工程学院,山东 东营 257000)
2017-05-30
黄 磊(1989—),女,山东东营人,中国石油大学胜利学院机械与控制工程学院助教,硕士,主要从事检测技术与自动化装置、流量计量研究。
10.3969/j.issn.1673-5935.2017.03.007
科氏流量计测量管振动频率检测及跟踪方法研究
黄 磊
(中国石油大学胜利学院 机械与控制工程学院,山东 东营 257000)
科氏流量计工作时需要测量管以其固有频率进行振动,这就需要将测量管的振动频率准确实时的进行测量,并且在整个工作过程中当测量管因为各种因素振动频率发生波动时,能够实时地跟踪其固有频率。针对科氏流量计模型,通过分析测量管频率检测及跟踪的方法,对过零检测法测频率和傅里叶变换法测频率进行仿真,比较两种方法的优缺点,然后根据傅里叶变换原理进行频率跟踪,模拟测量管固有频率变化时测量管频率跟踪情况,结果表明采用傅里叶变换法测量频率精度更高,利用傅里叶变换法进行频率跟踪可以较快跟踪测量管的固有频率变化。
科氏流量计;频率检测;频率跟踪;过零检测法;傅里叶变换法
科里奥利质量流量计是一种直接式质量流量计,除了测量质量流量之外,通常还要测量流体的密度。通过对测量管流体力学模型及振型分析[1-2],可以得出流体密度的表达式如下:

(1)
式中,ρ为流体密度;C和D为与测量管有关的量;t为测量管的主振动周期,即谐振周期;f为测量管的谐振频率,即固有频率。
(2)
其中,ρ′为测量管材料的密度;r1为测量管的内径;r2为测量管的外径;kc为取决于测量管结构和尺寸的量;E为测量管材料的弹性模量[3]。
由公式(1)可知测出测量管的谐振频率即可得出流体密度,所以在驱动测量管振动时,一般使测量管在谐振频率下振动,一方面方便测量流体的密度,另一方面可以用很小的驱动力得到较大的振幅,能量消耗最小。故测量管振动频率的检测及跟踪显得尤为重要[4]。
1 过零检测法测频率
过零检测法是指找出信号的过零点,将信号相邻两次经过零点的时间作差,这个时间差就是信号周期的一半,有了信号的周期就可以得到信号的频率。一般有基于硬件电路的过零检测法和基于软件算法的过零检测法。
基于硬件电路的过零检测,是通过硬件电路的过零比较得到一路方波信号,用单片机时钟对方波信号进行计时,得出相邻过零点的时间差,从而得到信号频率。
基于软件算法的过零检测法是找出信号零点附近的点,在信号的零点处,进行曲线拟合,计算出拟合曲线的过零时间,将相邻两个过零时间作差作为周期的一半,再计算出信号频率。
曲线拟合可以采用拉格朗日插值法,采用基于拉格朗日插值的过零检测法检测振动频率仿真结果(图1)。
按照过零检测法计算出来的频率是每个周期的频率,如果某些采样点出现问题或者某次计算出现失误会计算出错误的频率,这样会使根据该频率合成的驱动信号出现错误,影响测量管的振动。

图1 基于拉格朗日插值的过零检测法检测频率仿真图
假设通过某一方法计算出的频率值为:
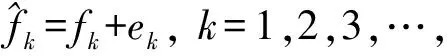
(3)


(4)
式中,k=5,6,7,…,N。
这样数据的误差变为:
(5)
式中,k=5,6,7,…,N。
通过逐次对数据取滑动平均,可以有效地减小频率计算的误差,使合成的正弦波的频率更加准确,增加了测量管振动的稳定性。
对图1中的频率进行滑动平均处理可得图2。

图2 频率滑动平均处理仿真图
比较图1和图2可以看出,经过滑动平均处理后,频率值更加平滑,波动更小,更加有利于测量管的平稳振动。
2 傅里叶变换法测频率
采用傅里叶变换法检测信号的频率一般分为粗测和细测两步[6]。先通过粗测大概确定测量管振动频率的范围,再细测出精确的频率值。
粗测时,选取采样频率fs1进行采样,采样N1个点,此时采样频率分辨率为:

(6)
将N1个采样数据进行如下傅里叶展开[7]:

IXC(k)-jIXS(k).
(7)
式中,k=0,1,2,3,…,N-1。


(8)
经过粗测得出频率的范围之后,进行频率细测。
改变采样频率为fs2,使fs1-f1 (9) 频率分辨率的范围为: (10) 改变采样频率fs2,计算每个采样频率对应的K2次谐波的强度,比较不同采样频率fs2时的K2次谐波强度,找出最大的谐波强度对应的采样频率fsmax,则振动信号的频率为: (11) 采用傅里叶变换法检测的信号频率如图3所示。 图3 傅里叶变换法检测频率仿真图 比较图2和图3可以看出,采用傅里叶变换法计算测量管振动频率,频率波动更小,误差也更小。这是因为采用过零检测法计算频率时,只用到了信号过零点附近的点。 得出信号的初始频率之后要不断检测信号的频率实现频率的跟踪[8]。根据初始频率检测得出的信号频率f0采样一个周期的信号,假设以fs的采样频率采样N个点,进行傅里叶分析,那么功率谱最大的是基波信号,其实部和虚部分别为a0和b0,通过离散傅里叶变换求得该采样周期内的相位为[9]: (12) 在下一个周期内,仍然以fs频率采样N个点,进行离散傅里叶变换,得出此时相位为: (13) 假设振动信号的频率不变,那么这两个相位θ1和θ2应该是相等的,如果相位θ1≠θ2,那么此相位差是由两个周期频率的差引起的[9],即: x(t)=Asin(2πf0t+2πΔft+θ1). (14) 采用傅里叶变换计算的相位差是整个采样时间内的平均相移,而2πΔft为瞬时相移,将2πΔft取N个采样值的平均: (15) 那么有: π(N-1)ΔfΔt=θ. (16) (17) 这样实时地根据计算出来的Δf改变合成的驱动波的频率,就实现了频率的跟踪。 在Simulink仿真中,改变测量管模型的频率,进行频率跟踪,仿真结果如图4。 从图4可以看出,频率发生变化时,采用傅里叶变换的方法进行频率跟踪,能够在频率发生变化之后的0.01 s内跟踪上频率变化,满足科氏流量计频率变化的需求。 图4 频率跟踪仿真图 (1)科氏流量计测量管的振动频率检测精度对流量计的正常稳定工作有重要影响。采用过零检测法检测频率方法简单,计算量少,但测量精度不够;采用傅里叶变换法测量频率计算量大,但测量精度更高。 (2)通过仿真验证了利用傅里叶变换原理进行频率跟踪可以较快跟踪测量管的固有频率变化,满足测量管频率变化的需求。 [1] SULTAN G, HEMP J. Modelling of the Coriolis Mass Flowmeter [J]. Journal of Sound and Vibration, 1989,132(3):473- 489. [2] BINULAL B R, RAJAN A, KOCHUPILLAI J. Dynamic analysis of Coriolis flow meter using Timoshenko beam element[J]. Flow Measurement and Instrumentation, 2016,47(3):100-109. [3] 肖素琴,韩厚义.质量流量计[M].北京:中国石化出版社,1999:32-74. [4] 杜明.一种基于改进自适应算法的科氏流量计频率解算新方法[J].工业计量,2014(3):64-68. [5] 裴益轩,郭民.滑动平均法的基本原理及应用[J].火炮发射与控制学报,2001(1):21-23. [6] 于翠欣,徐科军,刘家军.基于DFT的科里奥利质量流量计信号处理方法的改进[J].合肥工业大学学报(自然科学版),2000,23(6):935-939, 943. [7] JACOBSEN E, LYONS R. The sliding DFT [J]. IEEE Signal Processing Magazine, 2003,20(2):74-80. [8] 李苗,徐科军,侯其立,等.数字科氏质量流量计正负阶跃交替激励启振方法[J].仪器仪表学报,2010,31(1):172-177. [9] 徐科军,姜汉科,苏建徽,等.科氏流量计信号处理中频率跟踪方法的研究[J].计量学报, 1999,20(4):304-307. TH814 A 1673-5935(2017)03- 0022- 03 [责任编辑]李冬梅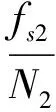



3 频率的跟踪


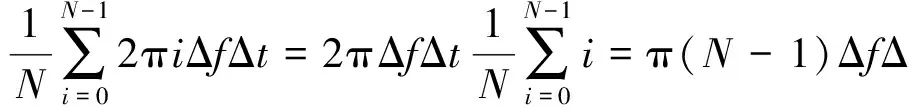


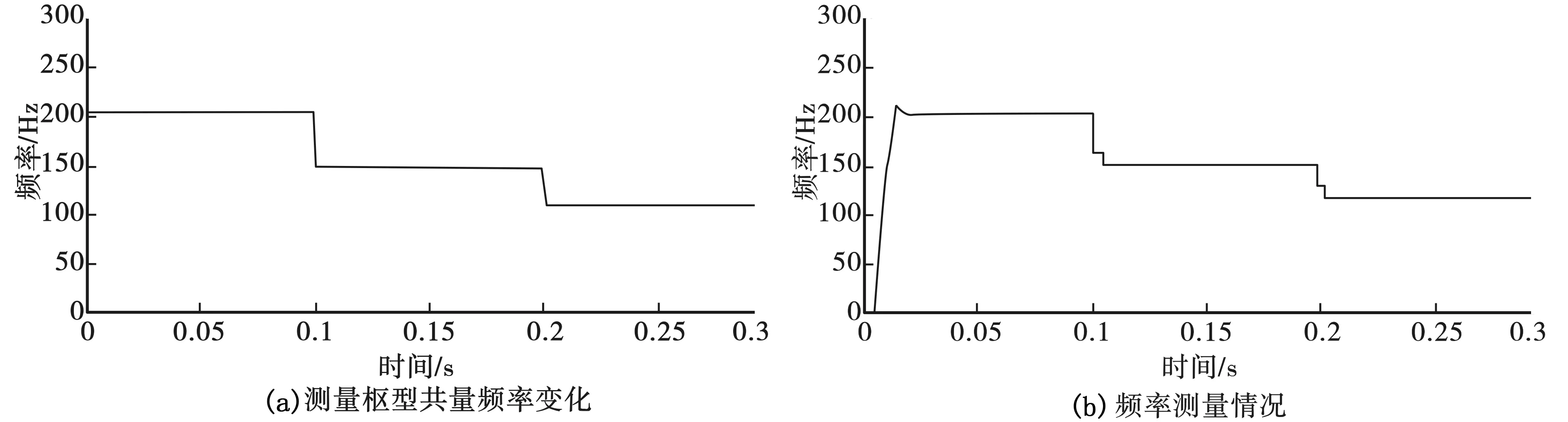
4 结 论

