基于ANSYS Workbench车用柴油发动机曲轴强度有限元分析
刘大龙,李稳迪,张瑞,杨锦旗,施伟辰
(上海海事大学物流工程学院,上海 201306)
基于ANSYS Workbench车用柴油发动机曲轴强度有限元分析
刘大龙,李稳迪,张瑞,杨锦旗,施伟辰
(上海海事大学物流工程学院,上海 201306)
曲轴是发动机主要的零部件之一,对发动机的整体可靠性及寿命都有很大的影响。利用SolidWorks软件建立某六缸车用柴油发动机曲轴3D实体模型,并基于ANSYS Workbench软件对曲轴进行有限元分析。对整体曲轴进行模态响应分析,得到其固有频率和固有振型。在低频状态下,曲轴主要发生弯曲变形;在高频状态下,曲轴主要发生伸缩扭转变形。随着频率增大,曲轴连杆轴颈与曲柄臂的连接处和主轴径与曲柄臂过渡圆角连接处的伸缩扭转变形越大,为曲轴的危险区域。以模态分析结果作为参考,重点分析了每个气缸在最大拉压工况下的应力分布,并校核了其疲劳安全系数。最终结果表明,此曲轴强度满足设计要求。
柴油发动机曲轴;有限元分析;模态响应;疲劳安全系数
0 引言
曲轴的工作条件及受力条件通常比较复杂,一般会受到活塞连杆的拉压力、自身惯性力、轴承支座的支撑力以及扭转振动等,这些条件都能使曲轴产生应力集中,从而使曲轴的整体性能大大下降,缩短其使用寿命,因此对曲轴性能进行研究就显得尤为重要。研究曲轴的方法主要有3种:分段简支梁法、连续梁法、有限元法[1]。分段简支梁法和连续梁法由于某些数据无法计算,所以最终结果的精度不能得到保证;有限元法将模型分为无数个小单元,通过计算各个单元上节点的位移可以精确得到曲轴的应力分布状态。此方法受到了国内外研究学者的肯定,为研究曲轴性能提供了很好的途径。吕端等人[2]对V8发动机进行了前10阶有限元模态分析;李学民等[3]通过模态敲击试验验证ANSYS Workbench所得到的模态分析结果;徐中华等[4]通过迭代法计算了曲轴的前10阶固有频率和振型;樊晓霞等[5]对六缸柴油机曲轴进行了前9阶模态分析;方宏生[6]通过曲轴有限元分析对曲轴进行了结构化改进;王良国等[7]对曲轴进行疲劳强度校核,并对曲轴的强化工艺进行了探讨;余小松[8]对原曲轴和变更曲轴进行疲劳强度校核;张健等人[9]对曲轴进行了应力分析,并对曲轴应力集中的倒角区域进行了优化;胡云萍等[10-11]对改进的曲轴有限元模型进行了疲劳强度分析;陈伟等人[12]采用两种曲轴模型方案对曲轴进行了疲劳强度校核;平学成等[13]对单拐曲轴进行了有限元分析;沈海涛等[14]采用弹簧单元模拟曲轴支撑,并对曲轴进行了强度分析。以上文献研究方法单一,仅仅对曲轴进行了单一的模态分析和应力分析。作者在前人研究基础之上,采用模态分析和疲劳强度分析相结合的方法,从动、静力学两个方面对整体曲轴进行了详细的分析:首先,对曲轴进行模态分析,得到曲轴的固有频率和固有振型以及曲轴上的危险区域;然后,在此基础之上对曲轴尤其是曲轴危险区域进行应力分析,并校核该曲轴的疲劳强度安全系数。文中的研究对曲轴的设计以及改进具有一定的指导意义。
1 曲轴模态分析
1.1 曲轴模型建立
利用SolidWorks软件建立曲轴的3D实体模型。由于曲轴的模型结构较为复杂,为了减少后期的计算量,文中采用简化的曲轴模型,省去了曲轴的油孔以及曲柄臂凸台结构;在曲轴的7个主轴径上建立模拟轴承支座,以模拟曲轴的工作环境。将建好的曲轴3D实体模型保存为IGES格式文件,导入到ANSYS Workbench中,对曲轴进行有限元分析。曲轴的实体模型如图1所示。

图1 曲轴实体模型
曲轴建模参数如下:
(1)主轴径直径Dj=100 mm;
(2)连杆轴颈直径r=82 mm;
(3)活塞直径Dp=126 mm;
(4)爆发压pmax=13.5 MPa;
(5)连杆质量mr=3.639 kg;
(6)活塞组质量mjz=3.471 kg;
(7)连杆中心距L=153 mm;
(8)连杆质心到大头中心距L2=64 mm。
1.2 曲轴有限元模型建立
建立曲轴有限元模型,如图2所示。曲轴材料采用45号钢,参数如表1所示。采用Solid186单元对曲轴进行网格划分,连杆轴颈与曲柄壁的连接处和主轴径与曲柄壁过渡圆角连接处均采用单元长度为3 mm的四面体网格;主轴径和连杆轴颈处采用单元长度为5 mm的四面体网格;曲柄臂处采用单元长度为8 mm的四面体网格;模拟轴承支座采用单元长度为
8 mm的六面体网格;共划分为459 896节点,300 424个单元。

图2 曲轴的有限元模型

密度/(kg·m-3)7850弹性模量/MPa206800泊松比μ0.3抗拉强度σb/MPa610屈服强度σs/MPa355
1.3 曲轴位移边界条件施加
根据曲轴的结构及实际工作情况,对曲轴施加约束:
(1)对曲轴模拟轴承支座施加固定约束;
(2)曲轴的各主轴受到轴承支座的支承,由于主轴承与轴承座之间依靠润滑油进行接触,所以设定两者间为摩擦接触,摩擦因数为0.05;
(3)曲轴的大端受止推轴承Z方向的约束,并且由于整个曲轴受热胀冷缩的影响,所以对曲轴大端进行X、Y方向的约束。
1.4 模态分析的理论基础
模态分析主要用于确定结构的固有频率和固有振型。曲轴模态分析属于无阻尼的模态分析,是典型的特征值问题,所以可得到自由振动为简谐振动的微分方程:

(1)
简谐运动微分方程u=ucos(ωit), 将其代入上式得:
(2)
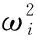
1.5 模态结果及分析
通过分析计算,得到了曲轴前12阶的固有频率和固有振型,表2为固有频率计算结果,图3为典型的振型图。

表2 固有频率计算结果
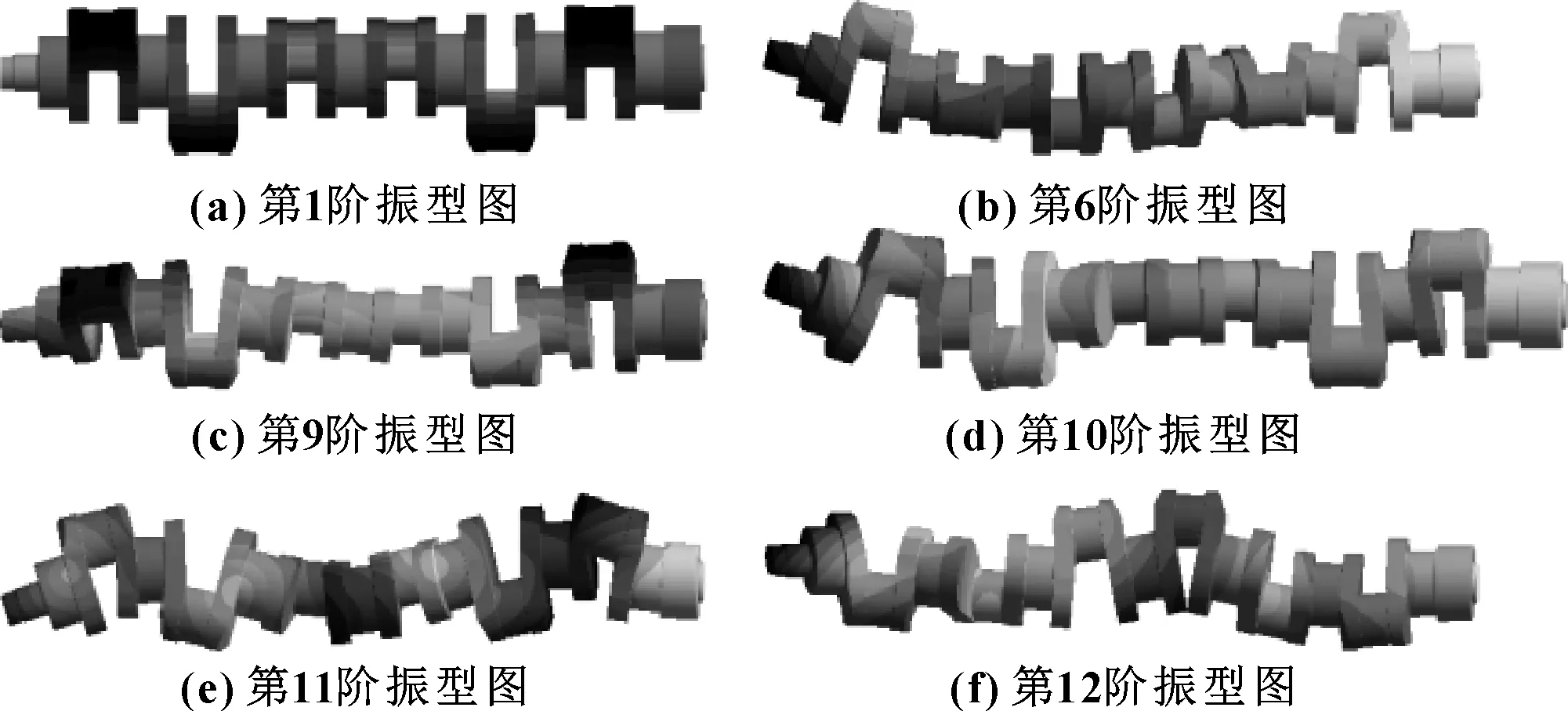
图3 曲轴模态振型图
第1阶固有频率为0,曲轴主要发生刚体扭转振动;从第2阶到第8阶,曲轴主要发生弯曲振动,随着频率不断增加其弯曲扭转变形逐渐增大;从第9阶到第12阶,曲轴主要发生伸缩扭转运动,随着频率不断增加其伸缩扭转变形也逐渐增大。
由以上结果分析中可以得出:在曲轴的工作过程中,在低频下主要发生弯曲变形,在高频下主要发生扭转变形,且频率越大其弯曲扭转变形越严重;其中变形区域主要集中在连杆轴颈与曲柄臂的连接处和主轴径与曲柄臂过渡圆角连接处,此两连接处主要发生应力集中现象,为曲轴的主要危险区域。
2 疲劳强度分析
2.1 载荷边界条件施加
曲轴工作条件以及受力条件都比较复杂。由模态分析结果表明:曲轴主要受弯曲载荷的影响,且连杆轴颈与曲柄臂的过渡圆角连接处和主轴径与曲柄臂过渡圆角连接处为曲轴的危险区域,通过静力分析对危险区域进行疲劳强度校核。曲轴所受弯曲载荷主要有以下3种:
(1)活塞连杆组作用到曲轴上的总压力Pg:
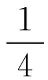
(3)
(2)连杆总成往复惯性力Pr1和活塞组的往复惯性力Pr2:
应用SPSS 19.0统计学软件分析本研究所有数据,计量资料的描述以均数±标准差表示,采用t检验或方差分析进行比较;计数资料的描述以率或构成比表示,采用卡方检验进行比较;生存曲线的绘制采用Kaplan-Meier法,生存率比较采用Log-rank检验,检验水准=0.05,以P<0.05表示差异具有统计学意义。
(4)
(5)
(3)连杆大头的旋转惯性力Pr3:

(6)
所以,曲轴在最大爆发压状态下所受的压缩载荷(最大受压载荷)为Q1:
Q1=Pg-Pr1-Pr2-Pr3=154 943.58 N
(7)
曲轴在进气冲程开始时所受的最大拉伸载荷(最大受拉载荷)为Q2:
Q2=Pr1+Pr2+Pr3=13 302.33 N
(8)
以曲轴每个气缸爆发时为计算工况,根据曲轴的实际工作情况及以往经验,假定压力沿连杆轴颈120°范围内均匀分布,故施加均布载荷[7]。由ANSYS Workbench分析计算曲轴的等效应力及其应力分布云图。曲轴主要受力情况如图4所示。

图4 连杆轴颈载荷分布示意图
2.2 计算结果
分析6个气缸分别在爆发工况时曲轴所受的拉压应力,并重点研究危险区域应力分布情况。
根据第四强度理论,可以得到曲轴的最大主应力,即等效应力。等效应力计算公式为:
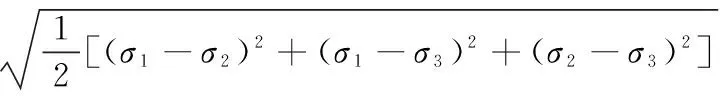
(9)
其中:σ1为第一主应力;σ2为第二主应力;σ3为第三主应力。
通过计算得到每个气缸发火状态以及进气冲程下曲轴的最大应力值,最大应力主要分布在连杆轴颈与曲柄臂的连接处和主轴径与曲柄臂过渡圆角连接处,如表3所示;图5、图6分别为第六气缸发火时压工况下和第五气缸进气冲程拉工况下的应力分布情况。
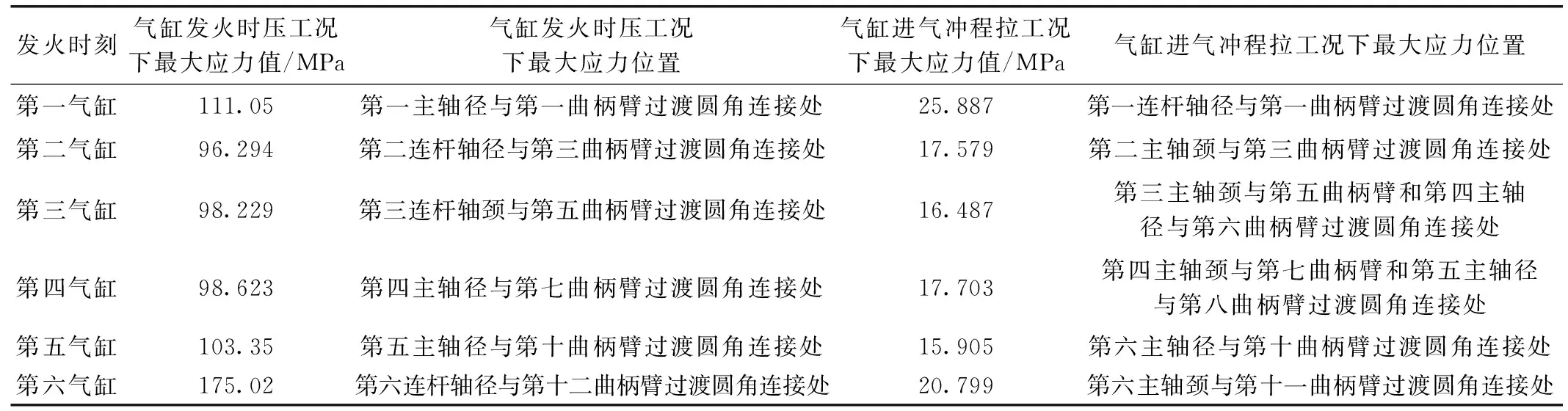
表3 各气缸爆发工况下最大应力值及最大应力位置

图5 第六气缸发火时压工况下的应力分布
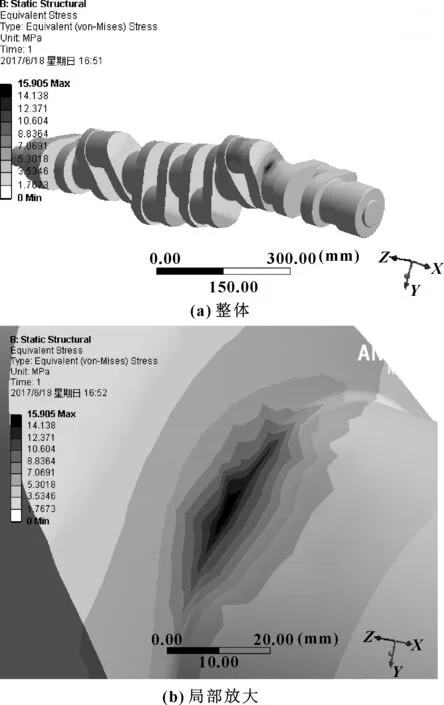
图6 第五气缸进气冲程开始时拉工况下应力分布
根据表3可以得出:曲轴在压工况下所受的最大应力值为175.02 MPa,出现在第六连杆轴径与第十二曲柄臂过渡圆角连接处;在拉工况下,最小应力值为15.905 MPa,出现在第六主轴径与第十曲柄臂过渡圆角连接处。经计算,得到应力幅值σa=79.547 5 MPa,平均应力值σm=95.452 5 MPa。由校核可知,曲轴的最大应力值均小于曲轴的抗拉强度σb=610 MPa和屈服强度σs=355 MPa,故曲轴的强度满足设计要求。
2.3 疲劳强度校核
曲轴在活塞的带领下不断绕主轴径轴心做高速旋转运动,依据上述计算结果对曲轴进行疲劳强度校核。
由于曲轴主要受弯曲载荷的影响,只校核曲轴在弯曲载荷下的疲劳安全系数。曲轴的疲劳安全系数计算公式:

(10)
式中:σ-1为45号钢弯曲疲劳极限,σ-1=300 MPa;kσ为有效应力集中系数,kσ=1.3;εσ为材料尺寸系数,εσ=0.745;βσ为强化系数,βσ=1.3;σa为应力幅值,σa=79.547 5 MPa;φσ为材料受弯曲特性,φσ=0.1;σm为平均应力,σm=95.452 5 MPa。
最终,经计算求得疲劳安全系数nσ=2.58。
考虑到多缸柴油机扭转弯曲振动会增加曲轴的应力,所以引入修正因子和动载系数对疲劳安全系数进行修正,修正因子和动载系数分别为λD=1.2和C=1.3。
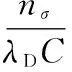
(11)
经计算得到曲轴修正安全系数n=1.65,由于曲轴设计许用安全系数为[n]=1.5,n>[n],所以该曲轴的疲劳强度满足工作要求。
3 结论
(1)对曲轴进行有限元模态分析,得到其在低频下主要发生弯曲变形,在高频下主要发生伸缩扭转变形,且随着频率的增加,主要变形区域连杆轴颈与曲柄臂的过渡圆角连接处和主轴径与曲柄臂过渡圆角连接处的变形愈发严重,为曲轴的危险区域。
(2)此六缸发动机曲轴主要受弯曲载荷的影响,分析每一个气缸爆发状态下曲轴的应力大小,最大值均分布在曲轴的危险区域。在曲轴压工况下,最大应力值为175.02 MPa,位于第六连杆轴径与第十二曲柄臂过渡圆角连接处;在拉工况下,最小应力值为15.905 MPa,位于第六主轴径与第十曲柄臂过渡圆角连接处。经计算,应力幅值为σa=79.547 5 MPa,平均应力为σm=95.452 5 MPa。所得到曲轴应力值均小于曲轴的抗拉强度σb=610 MPa和屈服强度σs=355 MPa,满足设计要求。
(3)利用ANSYS Workbench计算得到曲轴的应力大小,通过疲劳安全系数公式计算得到其疲劳强度安全系数nσ=2.58。由于考虑到多缸柴油机扭转弯曲振动影响,所以对疲劳安全系数进行修正,得到修正安全系数n=1.65,大于许用安全系数[n]=1.5,所以该曲轴满足设计要求。
(4)文中主要采用模态分析与疲劳分析相结合的方法,从动、静两个角度对曲轴进行分析,改善了以往单一的研究方式,从而更加准确地研究了曲轴的疲劳强度。
(5)文中的不足之处:文中计算结果基于有限元仿真,由于条件限制,缺乏实验数据支持;对曲轴有限元分析只在动、静两个角度进行了初步研究,相关研究还需进一步探讨。
(6)通过有限元分析计算得到曲轴的应力分布情况,并通过公式校核疲劳安全系数,为曲轴的设计及改进提供了重要的参考依据。
[1]孙军,桂长林,李震.内燃机曲轴强度研究的现状、讨论与展望[J].内燃机学报,2002,20(2):469-474.
SUN J,GUI C L,LI Z.A Review of Crankshaft Strength Analysis for Internal Combustion Engines[J].Transactions of CSICE,2002,20(2):469-474.
[2]吕端,曾东建,于晓样,等.基于ANSYS Workbench的V8发动机曲轴有限元模态分析[J].机械设计与制造,2012(8):11-13.
YU D,ZENG D J,YU X Y,et al.Finite Element Modal Analysis of V8 Engine Crankshaft Based on ANSYS Workbench[J].Machinery Design & Manufacture,2012(8):11-13.
[3]LI X M,CUI Z Q.Modal Analysis of 4-cylinder Engine Crankshaft Based on ANSYS Workbench[A].Journal of Measurement Science and Instrumentation,2015,6(3):282-285.
[4]徐中华,张茜,程伟.基于UG和ANSYS四缸曲轴有限元模态分析[J].机械工程与自动化,2009(4):17-19.
XU Z H,ZHANG X,CHENG W.Finite Element Modal Analysis of the Four-cylinder Crankshaft Based on UG and ANSYS[J].Mechanical Engineering & Automation,2009(4):17-19.
[5]樊晓霞,张建斌,李海刚.基于ANSYS的六缸柴油机曲轴的模态分析[J].机械设计与制造,2008(9):107-108.
FAN X X,ZHANG J B,LI H G.A Normal Model Analysis for a Six-crock Crankshaft Based on ANSYS[J].Machinery Design & Manufacture,2008(9):107-108.
[6]方宏生.基于有限元的曲轴分析计算及结构优化[D].杭州:浙江工业大学,2009.
[7]王良国,胡德波.368Q型发动机曲轴疲劳强度有限元分析[J].内燃机学报,2000,18(3):270-274.
WANG L G,HU D B.FEM Analysis on 368Q Crankshaft Fatigue Strength and Some Discuss on Relative Problems[J].Transactions of CSICE,2000,18(3):270-274.
[8]余小松.关于某发动机曲轴结构变更的强度分析[J].内燃机与动力装置,2016,33(3):50-55.
YU X S.Strength Analysis of Structural Modification of an Engine Crankshaft[J].Internal Combustion Engine & Power Plant,2016,33(3):50-55.
[9]张健,许福忠,郭小兰.基于ANSYS的发动机曲轴有限元分析[J].机电技术,2013(3):102-104.
[10]胡云萍,毛华永,胡玉平,等.6160柴油机曲轴三维有限元分析[J].山东大学学报(工学版),2006,36(2):99-103.
HU Y P,MAO H Y,HU Y P,et al.A 3 Dimension-finite Element Analysis on the Crankshaft of 6160 Diesel Engine[J].Journal of Shandong University(Engineering Science),2006,36(2):99-103.
[11]胡云萍,李国祥,胡玉平.基于三维有限元分析的柴油机曲轴优化设计[J].内燃机,2006(2):26-29.
HU Y P,LI G X,HU Y P,et al.Design Optimization of Diesel Engine Crankshafts Based on 3-D FEA[J].Internal Combustion Engines,2006(2):26-29.
[12]陈伟,温世杰,彭海熊.某V型发动机结构强度有限元分析及方案对比[J].铁道机车车辆,2011,31(S1):174-176.
CHEN W, WEN S J,PENG H X.Finite Element Analysis and Scheme Comparison on the Crankshaft Structural Strength of a V Engine[J].Railway Locomotive & Car,2011,31(S1):174-176.
[13]平学成,王小臣.基于ANSYS内燃机车柴油机曲轴三维有限元分析[J].内燃机与动力装置,2009(3):33-36.
PING X C,WANG X C.3 Dimension-Finite Element Analysis of the Crankshaft on Locomotive Diesel Based on ANSYS[J].Internal Combustion Engine & Power Plant,2009(3):33-36.
[14]沈海涛,郑水英,李志海.基于弹簧支撑的柴油机曲轴强度有限元分析[J].机械强度,2007,29(1):161-164.
SHEN H T,ZHENG S Y,LI Z H.Finite Element Analysis of Strength of Diesel Engine Crankshaft Based on Spring Support[J].Journal of Mechanical Strength,2007,29(1):161-164.
FiniteElementAnalysisforCrankshaftStrengthofaVehicleDieselEngineBasedonANSYSWorkbench
LIU Dalong,LI Wendi,ZHANG Rui,YANG Jinqi,SHI Weichen
(Logistics Engineering College, Shanghai Maritime University, Shanghai 201306,China)
The crankshaft is one of the main components of engine, and it has a great impact on the overall reliability and life of engine. The 3D solid model of a 6 cylinder vehicle diesel engine crankshaft was established by using SolidWorks software, and the crankshaft was analyzed by finite element analysis based on ANSYS Workbench software.Firstly,the modal response analysis of the crankshaft was made, the inherent frequencies and vibration modes were gotten.In the low frequency condition, the crankshaft bending deformation was mainly presented; in high frequency state,the torsional and expansion deformation was mainly presented.With the increase of the frequency,the torsional deformation of the connecting rod between the connecting rod journal and the crank arm transition fillet and the spindle diameter and the crank arm transition fillet were greater. Based on the results of the modal analysis, the stress distributions of each cylinder under the maximum tension and pressure conditions were analyzed emphatically,and the fatigue safety factor were checked.It is shown that the strength of the crankshaft can meet the design requirements.
Diesel engine crankshaft; Finite element analysis; Modal response; Fatigue safety factor
2017-06-19
刘大龙(1991—),男,硕士研究生,主要研究方向为机械设计。E-mail:liudalongchn@qq.com。
10.19466/j.cnki.1674-1986.2017.10.005
TH123
A
1674-1986(2017)10-020-05

