小卫星声-振联合试验耦合响应分析及预估
张 群,毕京丹,王英诚,卫 国,胡彦平
(北京强度环境研究所,北京 100076)
小卫星声-振联合试验耦合响应分析及预估
张 群,毕京丹,王英诚,卫 国,胡彦平
(北京强度环境研究所,北京 100076)
卫星在主动段承受发动机脉动推力和气动噪声激励复合作用下的振动环境。以整星模型为试验对象,分别开展了卫星的振动台随机振动试验、噪声试验和声-振联合试验。对3组试验结果的对比分析发现,声-振联合试验中,基础激励和噪声激励对不同结构处响应在低频段和中高频段具有不同的影响规律。在此基础上,提出了一种工程应用方法,即用振动台试验和噪声试验的响应极值包络法以及线性叠加法以预示声-振联合试验的响应。
卫星;振动环境试验;声-振联合试验;耦合响应
0 引言
卫星在发射及主动段飞行过程中将经受由火箭发动机脉动推力和整流罩气动噪声激励复合作用的振动环境。脉动推力激励的振动通过机械结构传递到卫星,气动噪声通过罩内空腔的空气振荡传递至卫星上。为了考核卫星及其有效载荷承受此环境的能力,通常采用振动台随机振动或噪声试验考核。选择做随机振动试验还是做噪声试验,目前仍存在分歧。GJB 1027指出,一般对于质量不超过450 kg的卫星,可以用随机振动试验代替噪声试验[1]。对于质量在 500~1000 kg的卫星,如何选择试验项目存在争议[2-4]。由于 2种激励的机理不同,彼此无法完全取代,尤其是二者的耦合试验,若选择其中的一种试验,则必然存在考核不充分、或不能呈现复合激励下振动耦合响应的情况。因此,有必要开展声-振联合环境试验[5-6]。
国内相关单位开展了一些声-振联合试验的研究。晏廷飞等[7]对某航天器的天线进行了声-振联合试验和单项试验的对比研究。杨江等[8]以太阳能电池阵为对象开展了声-振联合试验和仿真分析。张红亮等[9]对小卫星的太阳能电池阵开展了声-振联合试验。然而国内开展的声-振联合试验项目及研究尚缺对噪声试验、振动试验与声-振联合试验的差异性系统分析,不能完全反映3种试验对航天器整体结构考核的差异,对试验项目的选择也未能提供可靠的指导依据。
为进一步对比不同试验技术的效果,本文开展了卫星整星模型的声-振联合试验、噪声试验以及随机振动试验的对比研究,在组合体模型上各个关键部位设置测点并采集响应信号,以分析不同结构处3种试验的响应差异,尤其考查声-振联合激励环境试验考核的有效性,为后续航天器产品的力学环境试验项目及条件剪裁提供参考。
1 试验设计
1.1 整星模型
针对研究目的,试验件采用质量为600 kg的小卫星模型(如图1所示)。该模型主要由梁结构、板结构、承力筒结构及各种集中质量块组合而成,包括天线、太阳电池阵、承力筒、井字梁、横隔框、质量块、卫星支架等。集中质量块分布在井字梁和骨架上。天线为圆形结构,太阳电池阵为板壳结构,中心承力筒为圆柱形筒状结构(含仪器支架),卫星支架为锥段结构。

图1 用于振动环境试验的卫星模型Fig. 1 Satellite model for dynamic environmental test
1.2 试验原理
随机振动试验由电磁振动台完成。卫星通过工装固定于振动台上,将控制仪生成的驱动信号通过功率放大器逐级放大以驱动振动台,同时将控制点的响应信号反馈至控制仪,并与设定好的参考谱进行比较、修正,得到新的驱动谱;如此反复进行,直至控制谱满足试验控制精度要求。
噪声试验在混响室中进行。卫星模型放置在混响室的中心位置,用行波管支架进行弹性支撑。噪声环境经由控制仪生成的驱动信号通过功率放大器逐级放大,由噪声发生器产生,同时将控制点的声信号反馈至控制仪,并与设定好的参考谱进行比较、修正,得到新的驱动谱;如此反复进行,直至控制谱满足试验控制精度要求。
声-振联合试验是将振动台放置在混响室的中心位置,卫星通过工装固定于振动台上,试验时振动台和噪声源同时施加激励,并通过各自的反馈回路与控制谱对比修正,直至达到控制精度要求。
1.3 试验条件
本研究的试验项目安排了整星模型的随机振动试验、噪声试验和声-振联合试验。随机振动试验和噪声试验的试验条件均为实测谱,其中随机振动试验控制谱条件如图2所示,频率为20~2560 Hz,量级为4.93g;噪声试验的控制谱条件如图3所示,声压级为142 dB。随机振动的激励方向为卫星轴向(x向)。试验中选取的关键部位测点分别为天线罩、上盖板、太阳电池阵、柱段、柱段外质量块、2个井字梁、承力筒、隔板质量块、星箭界面、卫星支架、中心内质量块等共17处,测点位置及编号如图1中所示,编号中的“-3”表示3向(x、R、T)测点,R向为承力筒或天线罩的径向,T向为承力筒或天线罩的切向。

图2 随机振动控制谱条件Fig. 2 Random vibration control spectrum
整星模型组合体的支架下端面用密封板密封,采用图3的条件进行了噪声试验,之后又采用图2和图3的条件分别完成了随机振动试验和声-振联合试验。

图3 噪声控制谱条件Fig. 3 Acoustic control spectrum
2 试验结果及分析
由于随机振动的激振方向为x向,故将整星模型组合体的随机振动试验、噪声试验和声-振联合试验x向的测点响应进行对比,部分关键点的方均根响应结果如表 1所示,其中分析频率范围均为20~2560 Hz,另外还给出了将测点的振动试验和噪声试验两者的功率谱幅值相加后的新功率谱的方均根响应结果。

表1 噪声试验、随机振动试验和声-振联合试验关键测点的响应Table 1 Responses of main gauging points for noise test, random vibration test and vibro-acoustic test
对不同结构处测点的 3种试验响应进行对比统计(见图4),得到如下结果:
1)柱段外质量块与隔板质量块等处的响应规律基本一致。以图 4(a)柱段外质量块上的响应为例,随机振动试验响应与声-振联合试验的响应相近;从中低频段(大于 300 Hz)开始,随机振动试验的响应虽然衰减,但仍与声-振联合试验响应的结果相近;在整个频带上,噪声试验的激励效果都很小;声-振联合试验以振动台基础激励响应占主导。
2)天线罩、上盖板和太阳电池阵等处的响应规律基本相同。以图4(b)柱段外质量块上的响应为例,此处的随机振动试验响应与噪声试验响应的曲线出现交叉,将交叉处的频率定义为交越频率。在交越频率之前的低频段,声-振联合试验的响应以基础激励响应为主;高于交越频率(260 Hz)后,随机振动试验的响应衰减,高频激励效果很小,而噪声试验的激励效应增大,故在跨越交越频率后声-振联合试验的响应以噪声激励响应为主。
3)卫星支架、星箭界面、承力筒和井字梁等处的响应规律基本相同。以图 4(c)内部井字梁为例,低频段噪声试验激励的作用很小,主要以振动台的激励为主;从中低频段开始,噪声试验激励的响应开始增大并起主导作用,随机振动试验的响应有所衰减但仍起作用;500~1000 Hz三者的响应重合,说明在此频段这些结构处噪声激励和基础激励二者之间出现耦合作用,抑制了声-振响应的量级,而之后的高频段又以噪声激励起主导作用。
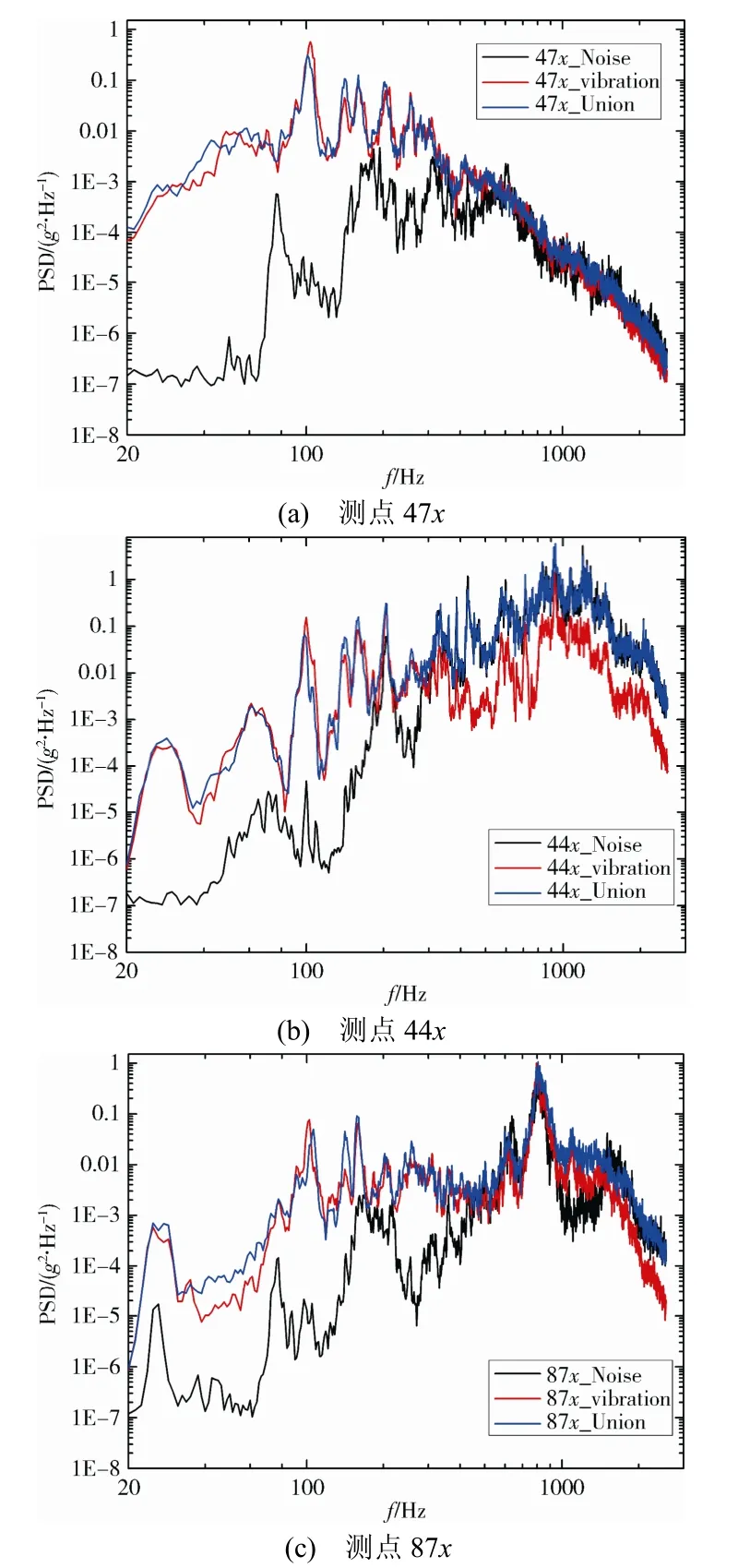
图4 不同结构测点处的3种试验的振动响应对比Fig. 4 Comparison of responses among random vibration test,noise test and vibro-acoustic test for different structural points
分析形成以上不同响应规律的主要原因如下:
1)不同的结构类型对噪声的敏感程度不同。表面积/质量比小的结构对噪声不敏感,对于该类结构,低频段的声-振环境可用随机振动近似考核;而表面积/质量比大的结构对噪声敏感,故该类结构高频段的声-振环境可用噪声试验近似考核。
2)噪声对结构的影响还与结构的空间位置有关。内部井字梁、卫星支架处虽然具有较大的表面积/质量比,但同时这些结构处于主传递路径上,存在振动与噪声的耦合响应。低频振动产生的变形对结构形成的应力,在一定程度上抑制了局部高频响应的极值;而中高频段的声-振耦合响应既有别于噪声试验结果也有别于随机振动试验结果,故这些结构处建议用声-振联合试验考核。
3 声-振联合试验响应预示
利用振动试验和噪声试验的实测数据,采用线性叠加法和极值包络法对声-振联合试验的响应进行预示。线性叠加法预示声-振联合试验响应功率谱是采用噪声试验和振动试验的响应功率谱值相加,极值包络法预示声-振联合试验响应功率谱是采用全频段内每个频率处取噪声试验和振动试验响应功率谱值中较大者。功率谱密度曲线和方均根对比结果分别如图5和表2所示。对图4中3个代表测点处的极值包络法、线性叠加法的预示结果与声-振联合试验实测结果进行对比。

图5 3个测点处的响应极值包络、线性叠加响应和实际声-振响应对比Fig. 5 Comparisons among the extremum envelope of responses,the superimposition of responses, and the actual vibroacoustic responses at three measurement points

表2 关键测点响应极值包络、线性叠加响应和实际声-振响应对比Table 2 Comparison among the extremum envelope of responses,the superimposition of responses and the actual vibro-acoustic responses at key measurement points
由对比结果可知,极值包络法和线性叠加法的结果除在低频段略低于声-振联合试验的结果,在其他频段都与声-振联合试验的响应结果基本相同,但中高频段线性叠加法的结果稍高于声-振联合试验的结果,这与噪声激励和基础激励的耦合作用分析一致:即在噪声响应开始占主导时,低频振动产生的变形对结构形成的应力,在一定程度上抑制了声-振联合试验中高频响应的幅值,并最终使叠加结果的方均根响应皆略大于声-振联合试验的结果。振动试验加速度响应规定的允差为10%,3种情形各测点的最大偏差见表2,相比之下,极值包络法的预示结果更为准确。
因此,可以用噪声试验和振动试验线性叠加以及极值包络的方法大致预示声-振联合试验的结果,其中极值包络法的预示结果更为准确。
4 结论
本文利用3种试验的结构响应对比研究,得到以下结论:
1)声-振联合试验中,不同结构处基础激励和噪声激励对低频段和中高频段的振动响应具有不同的影响效果,整体上低频段以基础激励的响应占主导,高频段以噪声激励的响应为主,但也会出现两者的耦合作用。
2)若考核星上设备,可选用随机振动试验或噪声试验;若考核整星或组合结构,各结构部位声-振响应规律不同,不能仅用随机振动试验或噪声试验代替,否则会导致部分结构过试验或欠试验,但可针对不同频段用2种试验的响应数据的极值包络法和线性叠加法相结合来大致预示声-振联合试验。
3)振动条件不仅在低频段起作用,对有些结构处,中高频的激励也有作用,需要制定较宽频带的振动条件;而噪声条件在交越频率以下基本不起作用,故可以适当提高噪声条件的起始频率。
以上结论为小卫星声-振联合试验考核方案制定和试验条件剪裁提供指导。
(
)
[1] 运载器、上面级和航天器试验要求: GJB 1027A[S], 2005
[2] SCHARTON T D. Vibration and acoustic testing of spacecraft[J]. Sound and Vibration, 2002, 36: 14-19
[3] FORGRAVE J C, MAN K F, NEWELL J M. Acoustic and random vibration test for low-cost missions[C]//Institute of Environmental Sciences: The 44thAnnual Technical Meeting. Phoenix, Arizona, 1998
[4] 沈志强, 晏廷飞, 张俊刚, 等. 卫星产品声振联合试验技术研究[J]. 航天器环境工程, 2015, 32(4): 395-399 SHEN Z Q, YAN T F, ZHANG J G, et al. The vibro-acoustic test technology for satellite[J]. Spacecraft Environment Engineering, 2015, 32(4): 395-399
[5] 宋文治. NASA在声振领域研究的新成果[J]. 强度与环境, 2006, 33(2): 58-64 SONG W Z. New achievements in the vibro-acoustic field of the NASA[J]. Structure & Environment Engineering, 2006, 33(2): 58-64
[6] Payload vibro-acoustic test criteria: NASA-STD-7001[S],1996
[7] 晏廷飞, 张俊刚, 方贵前, 等. 某航天器天线声振联合环境试验与单项环境试验对比研究[J]. 航天器环境工程, 2014, 31(2): 154-157 YAN T F, ZHANG J G, FANG G Q, et al. A comparison between vibro-acoustic environment test and single environment test for a spacecraft antenna[J]. Spacecraft Environment Engineering, 2014, 31(2): 154-157
[8] 杨江, 张俊刚, 方贵前, 等. 航天器组件声振联合环境试验与仿真技术[J]. 航天器环境工程, 2014, 31(4):369-373 YANG J, ZHANG J G, FANG G Q, et al. Vibro-acoustic environment test and its simulation for spacecraft components[J]. Spacecraft Environment Engineering,2014, 31(4): 369-373
[9] 张红亮, 王海明, 秦江. 小卫星太阳电池阵结构声振响应分析研究[J]. 航天器环境工程, 2015, 32(5): 521-526 ZHANG H L, WANG H M, QIN J. Structural vibro-acoustic response analysis of small satellite solar array[J]. Spacecraft Environment Engineering, 2015,32(5): 521-526
Analysis and estimation of satellite coupling responses in vibro-acoustic test
ZHANG Qun, BI Jingdan, WANG Yingcheng, WEI Guo, HU Yanping
(Beijing Institute of Structure and Strength, Beijing 100076, China)
The satellite encounters a vibro-acoustic environment in the powered phase caused by the pulsating and the thrust of the engine and the aerodynamic noise. The random vibration test, the acoustic noise test and the vibro-acoustic test are carried out separately for a satellite model. By comparing these results, it is found that at different frequency ranges, the base vibration and the acoustic noise have different effects on the structure's vibro-acoustic response. Based on this, a method is proposed to predict the vibro-acoustic response using the sum or the extremum envelope of the vibration and noise responses.
satellite; dynamic environmental test; vibro-acoustic test; coupling responses
V416.5
A
1673-1379(2017)05-0495-05
10.3969/j.issn.1673-1379.2017.05.007
2017-07-25;
2017-09-11
张群, 毕京丹, 王英诚, 等. 小卫星声-振联合试验耦合响应分析及预估[J]. 航天器环境工程, 2017, 34(5):495-499
ZHANG Q, BI J D, WANG Y C, et al. Analysis and estimation of satellite coupling responses in vibro-acoustic test[J]. Spacecraft Environment Engineering, 2017, 34(5): 495-499
(编辑:肖福根)
张 群(1988—),男,博士学位,研究方向为振动环境可靠性技术。E-mail: neaper@163.com。

