把握例题功能 做好例题教学

李光红

摘要：例题教学在数学教学中具有不可或缺的作用，利用例题可以引入新知、巩固新知、准确的示范、对所学知识拓展延伸等，根据例题的功能，采取不同教学方法，充分而有效地发挥例题的作用.

关键词：例题；功能；教学方法

数学离不开解题，数学教学也离不开例题教学.苏科版（2011）教材为师生提供了丰富的例题资源.教师若能充分利用好这些例题资源，充分挖掘其潜在的价值，将有助于巩固所学的知识，提升学生解题能力.纵观苏科版（2011）教材，可以发现这些例题主要有四种功能类型，下面就每一种类型分别谈谈如何进行相应的教学.

一.引入新知型

如九（下）《6.2黄金分割》例：如图1，点B在线段AC上，且 ，设AC=1.求AB的长.

图1

对于这个例题教师要引导学生抓住所给条件，利用方程思想，求出AB的长为 （近似值为0.618），并由此引入黄金分割、黄金比的概念，同时也复习了一元二次方程解决问题的知识.

这类例题，笔者认为教师要把握其“引入”作用，不宜做过多的拓展延伸.

二.示范引领型

如七（上）《3.3代数式的值》一课，例1：当a=-2，b=-3时，求代数式 的值.

教师要结合板书，进行讲解，准确的示范，总结解题步骤，提醒学生在代入数值时注意：（1）把数值代入时要把省略的乘号写出来；（2）字母的值取分数或负数时，在计算它的平方、立方，代入时要添上括号，在例题讲解后，往往要配以相应的练习，并进行评点，师生反思和总结.

一般来说，教科书例题的示范引领主要体现在两个方面：一是新知识应用的示范引领。教师借助例题，展示如何利用新知识解决问题，并通过例题的示范，使学生学会如何利用新知识分析、解决相关的教学问题。二是审题程序与表述规范的示范引领。教师通过例题展示解题过程和规范的表述示范，使学生明确解题表述的基本过程和规范要求，掌握解题的基本流程，从而形成良好的解题习惯和规范的语言表达能力。语言叙述是数学解题的重要环节，因此，语言叙述必须规范，规范的语言叙述要求条理清楚、步骤完整、详略得当、言必有据。数学本身有一套规范的语言系统，切不可随意杜撰数学符号和数学术语，课本例题为学生的解题规范作了最好的示范，而重视解题的规范化将为学生的数学学习带来积极的影响。

三.新课应用型

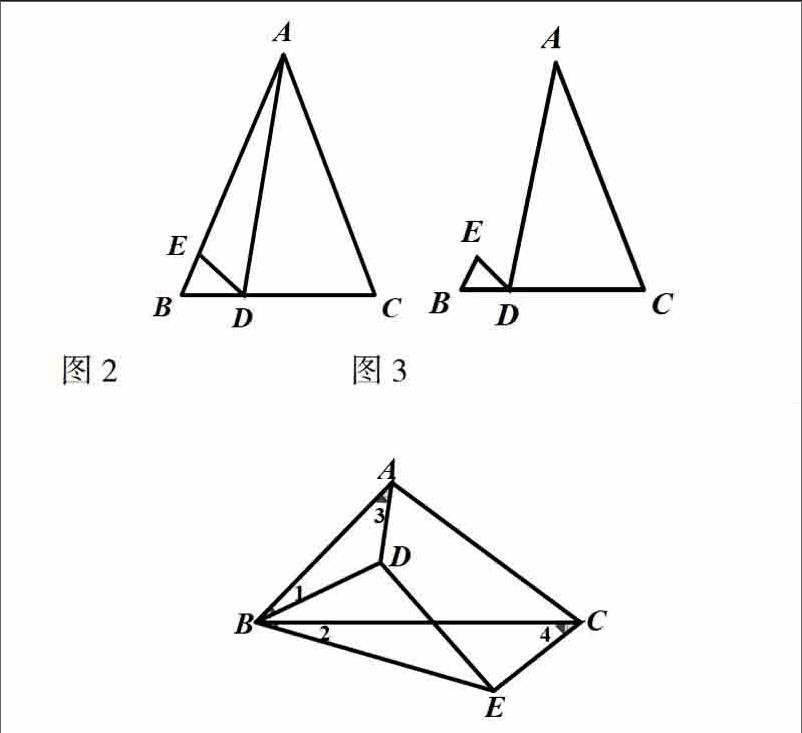
如九（下）《6.4探索三角相似的条件》例3：如图2，在△ABC中，AB=AC，点D、E分别在BC、AB上，且∠BDE=∠CAD.△ADE与△ABD相似吗？为什么？

首先要帮助学生分析思路：猜想△ADE与△ABD相似，根据本节课所学的判定方法：两角分别相等的两个三角形相似，要证△ADE∽△ABD，只要证得这两个三角形中有两组对应角相等，现在已有公共角∠DAE=∠BAD，还差一组对应角相等，我们可以考虑证明∠ADE=∠B.而题目所给的条件是AB=AC和∠BDE=∠CAD，结合三角形外角的性质得到∠ADB=∠CAD+∠C，再利用“等边对等角”和等式的性质，可以推知∠ADE=∠B.从而问题解决，然后要求学生写出解题过程.

这类例题的作用主要是知识点的巩固和应用，教学时，要着重引导学生学会分析，找出解决问题思路，并能有条理地书写出来，解后还要引导学生反思：本题用到哪些知识点，关键是什么，其中用到哪些数学思想方法，等等.另外还可以进行简单的变式训练和拓展.如本题可以追问：你能证明 吗？还有其它相似三角形吗？也可以把题目变为：在△ABC中，AB=AC，点D、E在BC、AB上，且∠ADE=∠C.问△BDE与△CAD相似吗？在此基础上还可以进一步得到基本图形，如图3，其基本条件是∠ADE=∠B=∠C，我们把它称之为“一线三泡泡”，结论是“左·右=左·右”（即BE·AC=BD·CD），这是一个十分有用的小结论.

四.拓展延伸型

如九（下）《6.4探索三角相似的条件》例：如图4，点D在△ABC内，点E△ABC外，∠1=∠2，∠3=∠4.△DBE与△ABC相似吗？为什么？

教学时要引导学生分析：△DBE和△ABC已经具备了什么条件？（由∠1=∠2可得：∠DBE=∠ABC）如果要用本课的定理：两边成比例且夹角相等的两个三角形相似，就必须证得： .那么怎样能得到：BD、BA、BE、BC這四条线段成比例呢？（用相似三角形）.对，我们就应证另外一组三角形相似，而题目已经给出∠1=∠2，∠3=∠4，所以可以证得：△ABD∽△CBE，于是得到 ，换一种形式就得到 .至此，障碍排除.接着引导学生书写一下解题过程.做好后，可以引导学生反思本题的特点：由条件先得到一组相似三角形，进一步得到两组对应边成比例，而这又为证明另一组三角形相似准备了“两边成比例”这一条件.后面可以举一些类似的例子：

变式1：如图5所示，BD、CE分别是△ABC的两条高，连接ED.求证：△AED∽△ACB.

变式2：本课练习3（改编）：如图6，在正方形ABCD中，E是AD的中点，点F在CD上，且CF=3FD.

①△ABE与△DEF相似吗？为什么？

②连接BF.△ABE与△EBF相似吗？为什么？

这类新课应用型问题，要引导学生分析思路，体会如应用所学知识解决问题，总结问题的特点、解题的方法，进行适当的变式训练，以期强化例题的辐射作用，做到“做一题，通一片”.为了培养学生思维的深刻性和广阔性，激发学生的学习积极性，教师结合教学的实际情况，适当地对课本例题的设问进行拓展延伸是非常必要的。“延伸”主要是指对例、习题进行变通推广，重新认识。恰当合理地延伸能营造一种生动活泼、宽松自由的氛围，开阔学生的视野，激发学生的情趣，有助于培养学生的探索精神和创新意识，并能使学生举一反三、事半功倍。

参考文献：

[1]王菊花.变式构造显本质 引领挖究提能力[J].中国数学教育（初中版），2016（7/8）：92-97.

[2]陈勇军.立足基本题型 变式深化思维[J].中学数学教学，2015（1）：55-58.endprint