基于支持向量机-CV的天然气水合物生成预测

宫清君， 马贵阳， 潘 振， 刘培胜， 李存磊

(辽宁石油化工大学 石油与天然气工程学院，辽宁 抚顺 113001)

基于支持向量机-CV的天然气水合物生成预测

宫清君， 马贵阳， 潘 振， 刘培胜， 李存磊

(辽宁石油化工大学 石油与天然气工程学院，辽宁 抚顺 113001)

天然气水合物的生成过程是一个多组分、多物态的系统，存在着复杂的结晶成核过程，需要考虑压力、温度、促进剂、搅拌速度等因素的影响，不但涉及动力学问题还涉及热力学问题，对其生成很难进行精确预测。基于支持向量机理论，结合实验数据，建立支持向量机预测模型来进行天然气水合物生成时的相平衡压力预测，采用平均平方误差、平方相关系数,以及平方绝对百分比误差和平均绝对误差等四种误差公式对预测精度进行评估，结果分别为8.370 08×10-5、99.897 6%、0.542 4%、1.990 0%，还对源数据进行了归一化([1，2])预处理以及利用交叉验证方法对核参数g(4)和惩罚因子c(1.414 2)进行了优化。模拟结果显示，由支持向量机预测模型得到的相平衡压力与实际实验获得的相平衡压力基本一致，预测效果较理想，证明该模型具有较高的准确性和可靠性。

天然气水合物； 结晶； 成核； 热力学； 支持向量机； 交叉验证

目前，国内外学者对NGH的形成条件做了大量的研究，拥有比较完善的预测模型，如国外的van der Waals和Platteeuw建立了具有统计热力学基础的vdW-P水合物模型等，国内的陈光进和郭天明提出的Chen-Guo水合物模型[6]。BP神经网络模型预测天然气水合物生成，是采用以经验风险最小化(Empirical Risk Minimize, ERM)的传统统计学理论为基础，这样容易降低BP神经网络的稳定性，甚至出现局部过优情况，对于那些小样本数据易导致学习机器泛化能力下降[7]。支持向量机(Support Vector Machine,SVM)是一种建立在VC维(Vapnik-Chervonenkis Dimension)理论和SRM准则基础之上的预测方法，更具体地说，SVM是结构风险最小化的近似实现，适合研究有限样本、非线性、高维度等方面的问题，比较适合于NGH的生成研究[8-10]。

本文在支持向量机引入天然气水合物生成预测的研究工作中，构建一个分类超平面作为决策曲面，使训练和测试之间的隔离边缘被最大化[11]，通过非线性核函数将实验所获得的数据样本空间映射到高维线性特征空间，并对模型进行训练和检验，对SVM在天然气水合物生成预测进行实用性研究，获得了具有重要研究价值的天然气水合物生成预测模型。

1 支持向量机的理论基础

1.1统计学习理论

支持向量机的理论基础是统计学习理论(SLT)，其核心内容是VC维、推广性的界、结构风险最小化(ERM)[12]。

(1) VC维 统计学习理论的核心部分是VC维，其定义是：如果函数集中的函数能够将一个指示函数集存在的b个样本分开成2b种形式，则称函数集能把b个样本打散；函数集能打散的最大样本数目b就是它的VC维。VC维反映的是函数集的学习能力。

(2)推广性的界 统计学习理论研究了各种类型的函数集，其理论指出：在最坏的分布情况下，实际风险与经验风险之间至少以1-η的概率满足以下关系式：

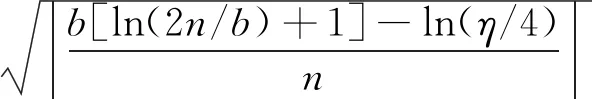
式中，R(W)是实际风险值，Remp(W)是经验风险值，b是函数集的VC维，n是样本数，η是显著性水平，(1-η)是置信水平。式(1)表明，实际风险由经验风险和置信范围两部分组成。置信范围受置信水平(1-η)、学习机器的VC维b和训练样本数目n的影响，所以式(1)可以记为：

以上研究经验风险与实际风险之间关系的系统就称为推广性的界。

(3) ERM 统计学习理论提出：在(1)式中，使Remp(W)最小，再折中考虑经验风险和置信范围之间的关系进而获得尽量小的b，最终使实际风险R(W)最小，即为结构风险最小化原则(ERM)。

1.2支持向量机(SVM)的学习机制

(1)支持向量(SV)

支持向量机是统计学习理论(SLT)最新的内容，也是目前最实用的部分。其研究最初是从线性可分问题开始的，即线性可分情况下的最优分类面，基本原理如图1所示[13]。图1中，空心点和实心点分别代表两类样本；L为分类线(面)，分别是过两类样本且离L最近的直线，L1、L2都平行于L，它们之间的距离叫做分类间隔。能保证Remp(W)最小的前提下将两类样本分开，且离两类样本的间隙最大的分类线(面)，称为最优分类线(面)，显然最优分类线的(1-η)最小。

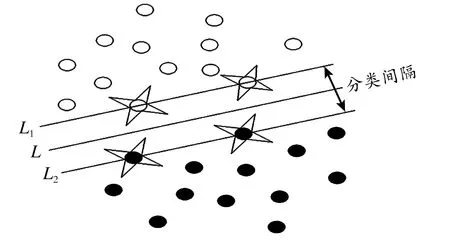
图1 线性可分下的SVM原理示意图

Fig.1SchematicdiagramoftheSVMprincipleoflinearseparable

分类线(面)方程为：

针对本文的回归问题，给定训练样本集为(Xi,yi),i=1,2,…,n,X∈Rn,y∈R,判别函数表示为：

式中,Φ(X)是从空间到高维特征空间的映射，ω为权值向量,h为一个偏量。将判别函数进行归一化处理，使两类样本都满足|g(X)|≥1,此时分类间隔为2/‖ω‖，进而求min(2/‖ω‖)即是求max(‖ω‖2),满足|g(X)|=1的样本点和满足max(‖ω‖2) 的分类线(面)就称之为最优分类面[13]，L1、L2上的训练样本点称作支持向量(SV)，图1中四个带四角形的点即是SV。

根据以上论述，可将求解最优分类面问题转化为优化问题：

再利用Lagrange优化方法将优化问题转化为对偶优化问题：

最终得到最优分类函数为：

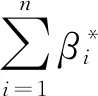
约束条件为：

式中，βi是每个样本对应的Lagrange乘子；h*是分类阈值，可任选一个满足式(5)中等号的支持向量。根据Karush-Kuhn-Tuckre定理可知：βi=0满足非支持向量，因此βi≠0满足支持向量。

(2) 支持向量机及其核函数的类型

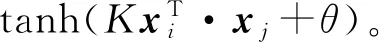
在引入核函数以后，以上各式中的内积形式全部用核函数代替，则(7)式中的最优分类函数变为：

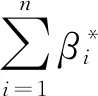
约束条件变为：

c是一个常数(惩罚因子)，控制错分样本惩罚的程度，式(9)就是支持向量机。

2 支持向量机天然气水合物生成预测模型

2.1支持向量机模型的建立及参数的确定

预测天然气水合物生成的源数据由实验所得，将源数据样本通过一个非线性函数映射到高维空间，通过这个映射转换可以进行数据序列的预测。整个算法可在MATLAB环境下编程实现。

源数据(18×8)记录的是与天然气水合物生成有关的各种指标，18行表示实验组数，8列分别表示每次影响天然气水合物生成的平衡压力、实验温度、实验初始压力、相平衡甲烷浓度、添加剂浓度、快速生成期时间、搅拌速度、注入水量。

根据模型编程可知天然气水合物的生成与前一次实验的平衡压力、实验温度、实验初始压力、相平衡甲烷浓度、添加剂浓度、快速生成期时间、搅拌速度、注入水量相关联，即选取第1—18实验组的实验温度、实验初始压力、相平衡甲烷浓度、添加剂浓度、快速生成期时间、搅拌速度、注入水量作为自变量，选取第2—18实验组的平衡压力作为因变量。

2.2数据预处理

在数据处理方面，首先对其进行归一化[16]预处理，采用的归一化映射如下。

式中，x,y∈Rn，xmin=min(x);xmax=max(x),即是使用mapminmax函数来实现。归一化的效果是原始数据被规整到[1，2]范围内，即yi∈[0,1],i=1,2,…,n，这种归一化方式称为[1，2]区间归一化。归一化方式有很多，而且不同的方式对最后预测结果的准确率也会有一定的影响，如表1所示。

由表1可知对数据采不采用归一化处理对结果的准确度几乎没什么影响，但是不采用归一化处理，无法读取平均平方误差数据。经过对比这几种归一化处理方式可知：[-1，1]归一化方式的c和g参数变化波动很大，不适合选用；[0，1]归一化方式和[-1，0]归一化方式差别很小，但是它们跟[1，2]归一化方式相比CVMSE的精度没有后者理想。综合以上因素，归一化方式选择[1，2]区间比较合适。

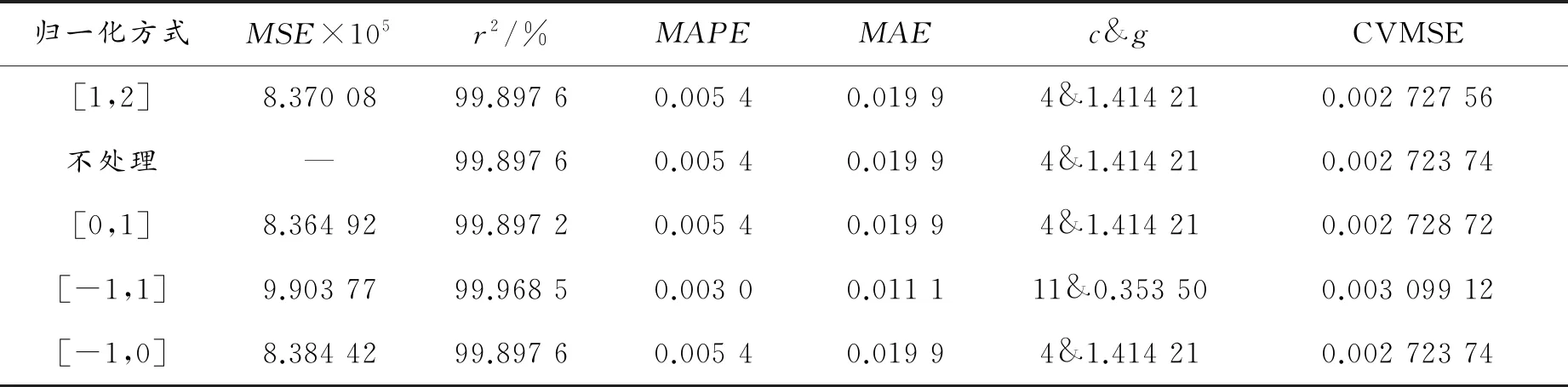
表1 采用不同归一化方式预处理数据结果对比Table 1 Comparison of data results with different normalization methods

说明：“—”是表示不存在。

2.3参数优化和选择

支持向量机的参数一般有SVM类型、核函数类型、不敏感损失函数、模型正规化参数以及核参数等[17]。笔者选用的SVM类型是epsilon-SVR(epsilon-Support Vector Regression),其需要事先确定参数-不敏感损失函数ε，此处设为0.01。又根据Vapnike的研究结果可知，核函数参数g和惩罚因子c是影响SVM性能的关键因素，通过交叉验证(Cross Validation，CV)方法中的一种(K-fold Cross Validation，K-CV)对其进行优化，得到最佳的参数g和c，之所以用K-CV优化，是因为其可以有效地避免过学习和欠学习现象的发生。

因为RBF核函数只含有一个参数σ2，所以该模型选择的核函数是RBF核函数，其比p阶多项式核函数和Sigmoid核函数的参数少一个，比较易于参数优化；其次是因为01)或者趋近于0(γ(xi·xj)+fcoe<1)。

在对惩罚因子c和核参数g进行初始粗略选择时，基于实验的考虑将最佳c和g的搜索空间分别设为cmin=-23,cmax=23,gmin=-23,gmax=23，即c、g∈[-8,8]，之后再利用SVMcgFor Regress进行精细选择，直到最佳交叉验证平均平方误差(Best Cross Validation Mean Squared Error，CVMSE)达到最佳值为止，如图2所示。

图2 惩罚因子c和核参数g选择结果

Fig.2Penaltyfactorcandkernelparametergselectionresults

图2(a)是详细选择的CVMSE二维等高线图，图2(b)是其3D视图，由图2可以读出CVMSE=0.002 727 6、c=4、g=1.414 2，具体数据见表2。

表2 SVM模型参数Table 2 SVM model parameters

3 模型预测结果及分析

对于支持向量机预测天然气水合物生成的评价标准有很多，本文采用了平均平方误差(MSE)、平方相关系数(r2),以及平方绝对百分比误差(MAPE)和平均绝对误差(MAE)来评价此模型的准确性，其方程式如下：

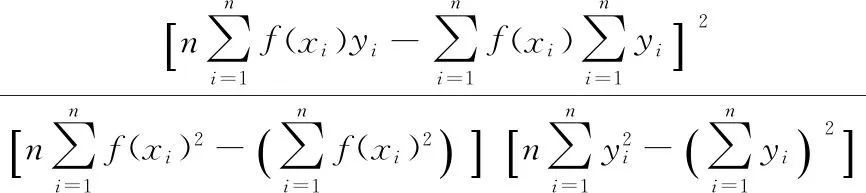
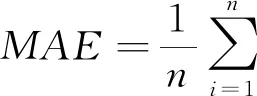
式中,n为样本数。

通过利用建立的SVM预测模型，对利用KDSD-Ⅱ型水合物动力学实验装置获得的影响天然气水合物生成的数据进行了预测，得到了其在天然气水合物生成达到相平衡时的平衡压力，如图3蓝线所示。

图3 原始数据与回归预测数据对比

Fig.3Comparisonofrawdataandregressionforecastdata

由图3可知，大部分预测点与实际值的相对预测误差都比较小(见表3)。由表3可知，原始数据与预测数据的相对误差均匀的分布在0附近，MAPE仅为0.542 4%，可见预测结果比较理想。

表3 天然气水合物生成预测结果Table 3 Predicted results of NGH formation

利用SVM-CV预测天然气水合物生成的评价数据如表4所示，可知此预测模型有较高的平方相关系数，平均平方误差、平均绝对百分比误差，以及平均绝对误差的值都比较低。

表4 预测评价表Table 4 Prediction evaluation table

4 结论

通过利用支持向量机模型对天然气水合物生成进行了预测，得到以下结论：

(1) 利用支持向量机预测天然气水合物生成，对NGH生成影响因素的源数据进行归一化预处理，并对利用其它归一化区间也进行了计算。得出此模型的归一化区间在[1,2]时精度值(0.002 727 56)最高。由于此模型的源数据比较平缓，跳跃性不是特别大，所以归一化的处理方式对预测天然气水合物生成时的相平衡压力影响并不明显。结合归一化计算结果，验证了归一化处理并不是绝对的，要根据具体情况分析。

(2) 选取的18组实验数据均来自于实验结果或者理论计算，利用这些数据对天然气水合物生成时的相平衡压力进行预测，预测结果与实验结果非常接近(见表3)，以及采用平均平方误差、平方相关系数、平方绝对百分比误差和平均绝对误差四种误差公式对预测精度进行评估，结果分别为8.370 08×10-5、99.897 6%、0.542 4%、1.990%，证明了支持向量机预测模型在天然气水合物生成预测的可行性。

(3) 提出了基于支持向量机(SVM)和交叉验证(CV)相结合的预测模型，说明支持向量机能够很好地解决对于小样本条件下的学习不足问题，并利用支持向量机理论对天然气水合物生成进行了预测，有助于天然气水合物的开采研究，为后续研究天然气水合物储存和运输提供了方法和基础，为将来的工业化运用提供了途径，有一定的实用价值。

[1] 赵洪伟，林君，业渝光. 海洋天然气水合物相平衡条件模拟实验及探测技术研究[D]. 吉林：吉林大学，2006.

[2] Naeiji P，Arjomandi A，Varaminian F. Optimization of inhibition conditions of tetrahydrofuran hydrate formation via the fractional design methodology[J]. Journal of Natural Gas Science and Engineering，2014，21：915-920.

[3] 车雯，梁海峰，孙国庆，等. 天然气水合物沉积层渗流特性的模拟[J]. 化工进展，2015，34(6)：1576-1581.

Che Wen，Liang Haifeng，Sun Guoqing，et al. Simulation study on the seepage characteristics of natural gas hydrate sediment[J]. Chemical Industry and Engineering Progress，2015，34(6)：1576-1581.

[4] 张刘樯，师凌冰，周迎. 天然气水合物生成预测及防治技术[J]. 天然气技术，2007，1(6)：67-68.

Zhang Liuqiang，Shi Lingbing，Zhou Ying. Formation prediction and prevention technology of natural gas hydrate[J].Natural Gas Technology，2007，1(6)：67-68.

[5] Dejean J P，Averbuch D，Gainville M. Intergrating flow assurance into risk management of deep offshore field[R]. OTC 17237，2005.

[6] 赵光华. CO2-N2-TBAB-H2O 体系水合物生成实验和模型研究[J]. 石油化工高等学校学报, 2016, 29(6): 11-17.

Zhao Guanghua. The formation experiment and modeling study of CO2-N2-TBAB-H2O hydrate system[J]. Journal of Petrochemical Universities, 2016, 29(6): 11-17.

[7] 蒋华琴，刘兴高. 免疫PSO-WLSSVM最优聚丙烯熔融指数预报[J]. 化工学报，2012，63(3)：866-872.

Jiang Huaqin，Liu Xinggao. Optional melt index prediction based on ICPSO-WLSSVM algorithm for industrial propylene polymerization[J]. CIESC Journal，2012，63(3)：866-872.

[8] Vapnik V N. Statistical Learning Theory [M]. Nwe York:Wcley,1998.

[9] Wu C H，Tzeng G H，Lin R H. A novel hybrid genetic algorithm for kernel function and parameter optimization in support vector regression[J]. Expert Systems with Applications，2009，36(3)：4725-4735.

[10] 张华，曾杰. 基于支持向量机的风速预测模型研究[J]. 太阳能学报，2010，31(7)：928-932.

Zhang Hua，Zeng Jie. Wind speed forecasting model study based on support vector machine[J]. Acta Energiae Solaris Sinica，2010，31(7)：928-932.

[11] 谷波，韩华，洪迎春，等. 基于SVM的制冷系统多故障并发检测与诊断[J]. 化工学报，2011，62(S2)：112-119.

Gu Bo，Han Hua，Hong Yingchun，et al. SVM-based FDD of multiple-simultaneous faults for chillers[J]. CIESC Journal，2011，62(S2)：112-119.

[12] 黄啸. 支持向量机核函数的研究[D]. 苏州：苏州大学，2008.

[13] Vapnik V著. 统计学习理论的本质[M]. 张学工，译.北京：清华大学出版社，2000.

[14] 奉国和. SVM分类核函数及参数选择比较[J]. 计算机工程与应用，2011，47(3)：123-124.

Feng Guohe. Parameter optimizing for Support Vector Machines classification[J]. Computer Engineering and Applications，2011，47(3)：123-124.

[15] 王强，田学民. 基于KPCA-LSSVM的软测量建模方法[J]. 化工学报，2011，62(10)：2813-2817.

Wang Qiang，Tian Xuemin. Soft sensing based on KPCA and LSSVM[J]. CIESC Journal，2011，62(10)：2813-2817.

[16] 梁家政，薛质. 网络数据归一化处理研究[J]. 信息安全与通信保密，2010(7)：47-51.

Liang Jiazheng, Xue Zhi. Standardized processing based on network data[J].Information Security and Communications Privacy，2010(7)：47-51.

[17] 李红英. 支持向量分类机的核函数研究[D]. 重庆：重庆大学，2009.

Prediction of Natural Gas Hydrate Formation Based on Support Vector Machine (SVM)-CV

Gong Qingjun， Ma Guiyang， Pan Zhen， Liu Peisheng， Li Cunlei

(PetroleumandNaturalGasEngineering，LiaoningShihuaUniversity，FushunLiaoning113001，China)

Natural gas hydrate has the advantages of abundant reserves, large calorific value and low emission, which can mitigate the environmental pollution problems caused by traditional fossil energy. The generation process of natural gas hydrate form is a system with multi-components and multi-physical states. The nucleation process is complex, which needs to consider the effects of pressure, temperature, promoters, stirring speed and so on. It is difficult to accurately predict the hydrate formation, because the hydrate formation process not only involves thermodynamics problems but also dynamics problems. In our paper, the support vector machine theory combined with experimental data was used to establish support vector machine prediction model for predicting natural gas hydrate equilibrium pressure. The prediction accuracy was estimated by using the mean square error, the square correlation coefficient, the square absolute percentage error and the average absolute error. The results are 8.370 08×10-5，99.897 6%，0.542 4%，1.990 0%，respectively. The pre-treatment origin data were normalized ([1，2]) and the nuclear parameterg(4)and punishment factorc(1.414 2) were optimized by using cross validation methods. Simulation results show that the equilibrium pressure obtained by support vector prediction model is good in agreement with the equilibrium obtained by experiments. The better ideal prediction effects prove that the model has advantages of accuracy and reliability. It can provide certain reference for research on natural gas hydrate in future.

Natural gas hydrate； Nucleation； Dynamics； Thermodynamics； Support vector machine； Cross validation

1006-396X(2017)05-0080-06

投稿网址：http://journal.lnpu.edu.cn

TE89

A

10.3969/j.issn.1006-396X.2017.05.015

2017-02-06

2017-02-28

国家自然科学基金项目(41502100);辽宁省高等学校优秀人才支持计划项目(LJQ2014038)。

宫清君(1986-)，男，硕士研究生，从事天然气水合物研究；E-mail：1449611564@qq.com。

潘振(1981-)，男，博士，副教授，从事油气储运方面研究；E-mail：28335719@qq.com。

(编辑 王亚新)

天然气水合物(Natural Gas Hydrate，NGH)是由天然气与水在高压低温条件下形成的类冰状结晶物质[1]，主要分布于海底大陆架边缘和冻土层中。1 m3的NGH大约可分解出160 m3天然气(标准状态下)，其碳含量约为现有化石燃料总和的2倍，是最具商业开发前景的清洁能源之一[2-3]。NGH若在天然气集输中形成会增加管道的输送阻力、减少输送天然气量甚至加大管件的毁坏程度；若在天然气开采中形成很可能会造成井筒的堵塞，所以有必要对NGH的生成预测进行研究[4-5]。