变形后阿尔奇公式在特低渗储层解释中的应用

田 秘，侯正猛，李占东，胡秀全

(1.东北石油大学 石油工程学院， 黑龙江 大庆 163318； 2.德国克劳斯塔尔工业大学，德国 克劳斯塔尔 610065；3.新疆油田公司 凤城油田， 新疆 克拉玛依 834000)

变形后阿尔奇公式在特低渗储层解释中的应用

田 秘1，侯正猛2，李占东1，胡秀全3

(1.东北石油大学 石油工程学院， 黑龙江 大庆 163318； 2.德国克劳斯塔尔工业大学，德国 克劳斯塔尔 610065；3.新疆油田公司 凤城油田， 新疆 克拉玛依 834000)

阿尔奇公式自提出以来，一直被广泛应用于测井饱和度解释领域，并取得了卓越的成果。针对特低渗透储层孔隙结构复杂、胶结程度高、孔隙曲折程度难以掌握等特点，直接利用阿尔奇公式计算含水饱和度有较大误差。通过调研大量文献以及对现场岩心资料的分析，将渗透率引入阿尔奇公式后对其进行修正，建立了适用于特低渗透储层的阿尔奇公式，同时得到了适合特低渗透储层的胶结指数与导电系数，探讨了特低渗透储层特性对岩电参数以及地层因素的影响。这为阿尔奇公式在测井饱和度解释方面的应用做出了更大范围的推广，使其在特低渗透储层的解释方面更为精准。

特低渗透；胶结指数；阿尔奇公式；地层因素

在国内已开发的油田中，低渗透油田占据了很大比重，目前我国已经形成了一套具有自主知识产权的低渗透油田勘探开发技术。随着开发年限的增加，开采难度越来越大，当注水开发油田进入高含水甚至特高含水阶段后，为提高最终采收效率，必须精准掌握剩余油分布情况，动态监测含水饱和度便成为油田生产管理中必不可少的工作。含水饱和度求取方法主要有等效岩石阿尔奇模型法、时间推移测井法以及普通取心测试法等[1-6]。其中，阿尔奇公式是最常用的主导方法。由于此方法理论上主要针对未水淹纯砂岩高孔高渗储层，因此对其他性质储层，虽然阿尔奇公式依旧适用，但岩电参数在数值上有很大范围的变化，且对于含水饱和度的计算精度很难达到油田开发、特別是中后期开发调整的要求。特低渗储集层物性较差，渗透率一般在1～10 mD，常常伴有低孔的特点，以孔隙度小于15%的居多，且特低渗储层胶结程度高，胶结类型复杂，以上因素导致不能直接利用公式中的经验岩电参数去求取含水饱和度，因而对该项工作造成了很大困难[7-9]。为此，笔者针对特低渗透储层特点，借助阿尔奇公式的基本理论，通过分析储层结构与各参数之间的关系，结合现场岩心资料模拟出适应其特点的变形公式及修正后的岩电参数。

1 阿尔奇公式修正

阿尔奇公式由地层因素与电阻率增大系数两部分组成，是地层因素F、电阻率增大系数I、孔隙度φ、含水饱和度S和地层电阻率之间的经验关系式。它是通过测井解释的储层流体与地层岩石电阻率来研究储层流体饱和度的一种方法，同时也是测井解释油水层的基础。因此，此公式在测井解释领域占据重要的地位。

1.1 阿尔奇公式及参数

地层因数

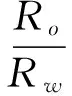
(1)

电阻增大系数

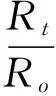
(2)

其中：Ro为100%饱和地层水时的地层电阻率；Rw为地层水电阻率；a为与岩性有关的导电系数；Rt为含油气地层电阻率；m为与孔隙结构有关的胶结指数；b为与岩性有关的参数；n为与含水程度有关的饱和度指数。

在纯砂岩理想情况下参数a=1，而对于泥质砂岩一般有a<1。理论上a的取值范通常在0.6～1.5。参数m反映储层孔隙与储层骨架的曲折程度，高纯度砂岩储层含有少量的胶结物，以粒间孔隙为主，孔隙大、喉道粗、连通性较好，此时m=2；而对于其他类型储层，由于泥质含量、胶结程度与岩性物性的变化，m值的变化范围较大，但一般处于1.5～3[10-15]。在没有通过确定岩电实验取得参数时，通常a、m的值应根据各地区、各种地层的统计结果确定，常见几种岩石的a、m值列于表1中可供参考。b是与岩性有关的参数，理论值b=1。n是与含水程度有关的饱和度指数，对于早期一次采油的未水淹油层，理论上n=2，然而对于后期注水开发的油田，地层水离子数发生改变，会引起n值的变化。由于此次研究主要针对地层因素F以及参数a、m进行定量分析修正，暂不对电阻率增大系数I以及参数b、n进行讨论。

以往在没有岩电实验来确定参数的情况下，按理论值计算的饱和度结果与实际测井解释值有很大偏差，因此针对不同岩性物性以及不同开发阶段的储层，要根据其自身特点确定岩电参数。

表1 胶结系数m与岩性系数a数值

1.2 地层因素公式修正

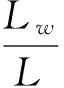
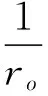
(3)

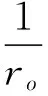
(4)

其中：rma为岩石骨架电阻；rw为孔隙内流体的电阻。

根据电阻率公式,式(4)可化为式(5)：

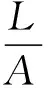
(5)

由于孔隙度φ=Vφ/V，则此时由式(5)及体积公式，可将地层因素公式化为式(6)。

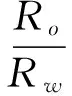
(6)

由式(6)可见，地层因素与孔隙度成负相关性，与孔隙曲折度成正相关。而曲折度可以反映孔隙中相互连通孔隙的渗透程度，曲折度越低渗透性越好，反之越差，因此曲折度与渗透率成负相关。综合以上，地层因素与孔隙度、渗透率均成负相关，但在以往计算饱和度时并未将渗透率考虑入内，导致对于受渗透率影响较大的特低渗透储层缺失最重要的解释参数。为此，笔者尝试将渗透率引入地层因素公式，导出公式(7)，通过渗透率的变化分别研究其对F、a、m的影响。

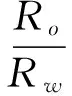
(7)

2 应用实例

2.1 参数选取

实例区处于松辽盆地南部中央坳陷内，属于向斜区构造，长期处于油气运移的指向区，成藏条件十分有利[17]。但由于纵向非均质性强，层间矛盾突出，导致纵向油层动用不均；虽然储量基础大，但采出程度低，综合含水高[18-20]；G油层为该区块的主力油层，根据该油层岩心资料统计显示，储层碎屑成分以石英为主，主要孔隙类型为粒间孔隙和微孔隙，主要胶结类型为再生-接触胶结、再生-孔隙胶结及孔隙胶结。通过139块G油层岩心的分析统计结果，可知细砂含量平均为15.64%，粉砂含量平均为59.71%，泥质含量平均为24.66%，孔隙度主要分布在10.0%～21.0%，空气渗透率主要分布在0.7～2.9 mD，属于中-低孔、特低渗-超低渗透储层(图1)。

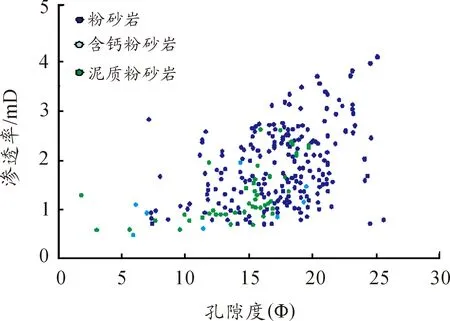
图1 G油层岩心岩性与物性关系

2.2 公式应用及探讨

G油层渗透率平均在1.65左右，属于特低渗透油藏，因此渗透率对储集空间影响较大。按上述参数，挑取孔渗相对集中的具有代表性的97块样品进行试验，分别按照式(1)以及变形后式(4)在双对数坐标中将其绘制出(见图2、3)，对a、m进行实测，具体数值见表2。

由计算结果可以看出：由式(1)实测的孔隙度与地层因素相关性较差，数据点较为离散(图2)。同时，由于泥质粉砂岩的存在，导致岩性系数a小于1，m偏高值与常规参数不同，这可能是由于特低渗透储层胶结程度高、颗粒间排列复杂、孔隙曲折度高导致的。为此，利用公式变形后的阿尔奇公式(4)对a、m值进行校正。对比校正前，校正后的相关性较高，a值更接近理论值1，m值更接近理论范围。

由以上结果可见：校正前后m值均大于2，a值均小于1，这也与表1中的常规理论相符，随着胶结程度增加，m值增大，a值减小。而特低渗透储层地层因素值较一般中孔中渗储层要大很多，周荣安认为纯砂岩储层地层因素值一般在100左右。通过本次分析认为，这应该是由于特低渗透储层自身的低孔特征引起的，由于泥质粉砂岩与含钙粉砂岩的存在，使得储层总孔隙程度降低，低孔导致岩石骨架增大，造成电阻率增加，进而引起地层因素增大。由此可见，变形后的阿尔奇公式的引出使得渗透率直接参与到储层特性与电阻率的关系中，对导电系数以及胶结指数进行了校正，使得岩电参数更符合特低渗透油藏特点，同时也解释了地层因数值较高的原因。

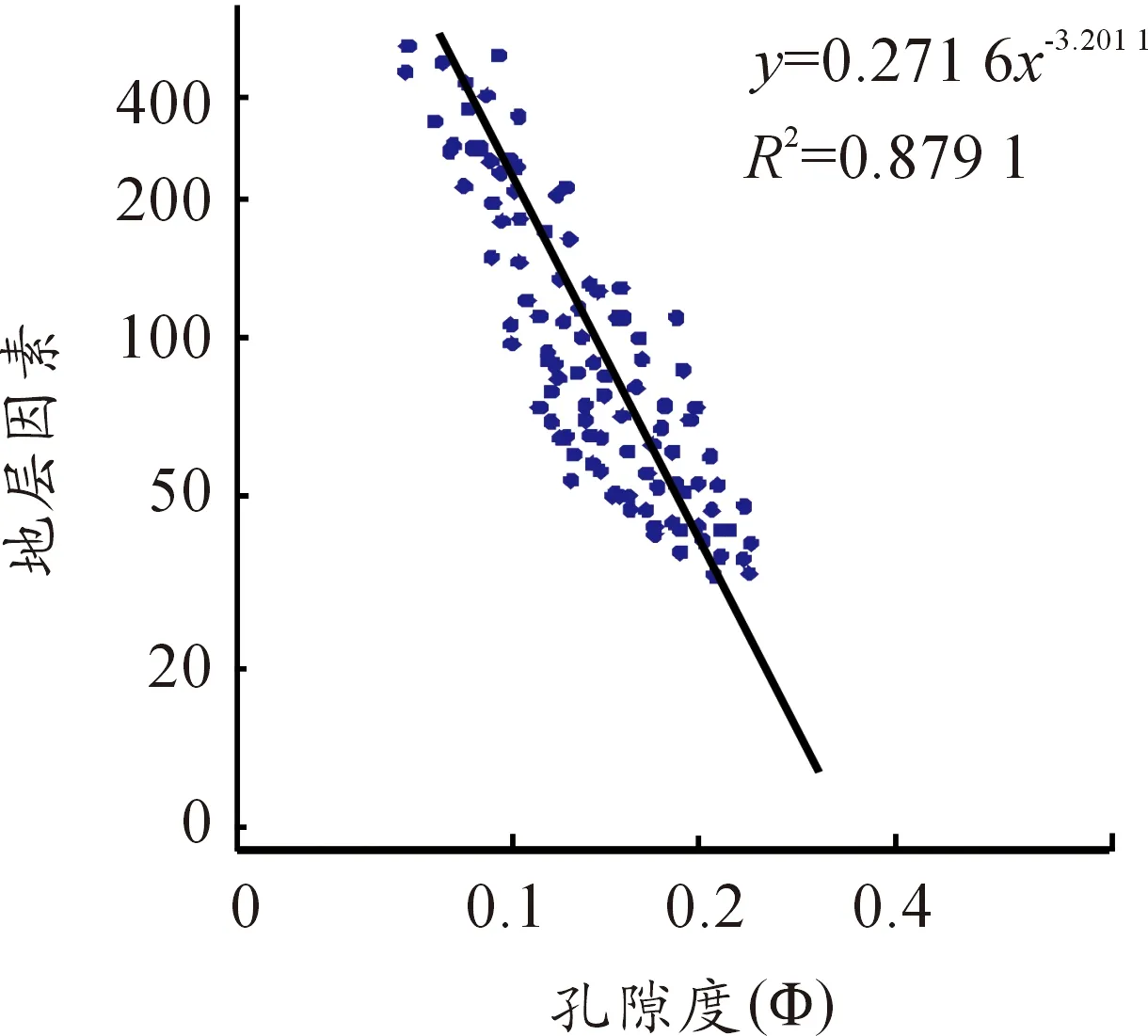
图2 孔隙度与地层因素关系

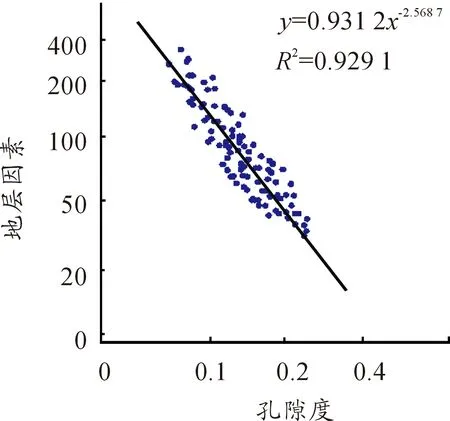
图3 变形后孔隙度与地层因素的关系

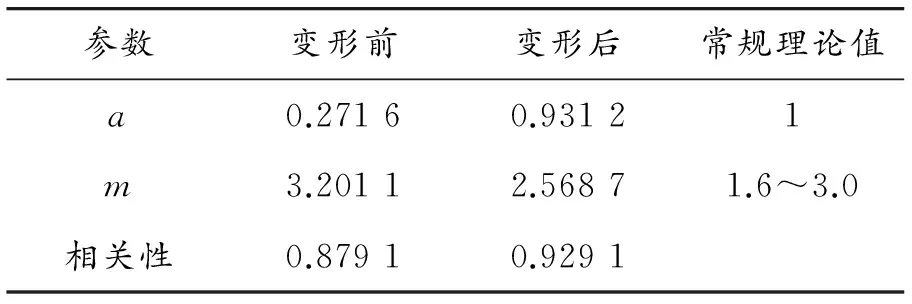
参数变形前变形后常规理论值a0.27160.93121m3.20112.56871.6～3.0相关性0.87910.9291

3 模型精度验证

根据G油层密闭取心资料对含水饱和度进行解释，同时与变形后的阿尔奇公式所计算的含水饱和度进行对比分析(图4)。从结果来看，变形后阿尔奇公式计算值在59.8%～65.7%，平均值62.5%，对比实际测量值在58.3%～67.8%，平均值64.2%，两种测量方式在曲线形态上保持良好的一致，相似度较高，误差值控制在3%以内。尽管还没有权威理论可以认定此种算法可行，但在数值上是等效的，因为对于特低渗透储层而言，渗透率在数值上很小，渗透率的引入不会对公式的整体结果造成很大的波动，反而可以起到校正作用。就目前分析来看，这种转换对于特低渗透储层，可以提高阿尔奇计算的精度，增加公式的稳定性，因此认为此种计算方法合理。

4 结论

1) 特低渗透储层非均质性强，粒度分布不均，导致孔隙度低，孔隙曲程度高，胶结物含量高，因此常规的岩电参数对特低渗透储层不再具有适用性。但渗透率的引入增加了地层因素与孔隙度关系的稳定性，提高了阿尔奇公式的计算精度，从本次研究结果来看，此改进方法对于特低渗透储层具有独特的适用性。

2) 由孔隙度与地层因素关系可以看出：特低渗透储层地层因素最大值在400左右，普遍高于纯砂岩储层。由于泥质砂岩及含钙砂岩的存在，这两种岩性的孔渗都极低，而地层因素与孔渗均成负相关，因此孔渗的降低必然会引起地层因素值的提高。

3) 由于特低渗透储层渗透率极低，在数值范围上极小，因此渗透率的引入不会使公式计算的结果产生很大的波动。正如本文中利用修正公式求取的导电系数与胶结指数更接近理论范围，以此计算出的含水饱和度与实际测量结果高度一致，误差能控制在3%以内，因此在数值上具有等效性。

[1] 谷宁,朱学谦,邢丽雯.非常规气储量计算方法分析[J].天然气与石油,2014(6):45-49，11.

[2] 陈志明,蔡雨桐,刘冰,等.低渗透岩石渗流规律的实验研究方法[J].天然气与石油,2012(3):49-52，101.

[3] 刘国霖,孔玉明,沈蔚,等.低渗透储层水锁伤害解除技术室内研究[J].天然气与石油,2012(4):67-69，102.

[4] 黄小平,柴婧.阿尔奇公式在泥页岩地层含油饱和度计算中的应用——以沾化凹陷沙三段下亚段为例[J].油气地质与采收率，2014(4)：58-61，115.

[5] 李占东,李阳,刘云利,等.松辽盆地南部东南隆起区白垩系登娄库组沉积特征[J].石油与天然气地质，2014(3)：401-409.

[6] 杜新龙.低渗透砂岩油层微流动机理研究[D].成都：西南石油大学，2012.

[7] 李功强,张军,胡瑶,等.致密砂岩孔隙度-电阻率关系与地层因素计算方法研究[J].地球物理学进展，2016(2)：695-700.

[8] 张振城,孙建孟,马建海,等.阿尔奇公式中a,m值对饱和度计算结果的影响[J].石油大学学报(自然科学版)，2004(6)：27-30，34.

[9] 李秋实,周荣安,张金功,等.阿尔奇公式与储层孔隙结构的关系[J].石油与天然气地质Oil & Gas Geology，2002(4)：364-367.

[10] 李占东,王义军,胡慧婷,等.松辽盆地北部青山口组一段泥页岩储集层特征[J].新疆石油地质，2015(1)：20-24.

[11] 李占东,王殿举,张海翔,等.松辽盆地南部东南隆起区白垩系泉头组典型河流相沉积特征[J].石油与天然气地质，2015(4)：621-629.

[12] 李占东,卢双舫,李军辉,等.松辽盆地肇源—太平川地区白垩系姚家组一段沉积特征及演化[J].中南大学学报(自然科学版)，2011，12：3818-3826.

[13] 周荣安.阿尔奇公式在碎屑岩储集层中的应用[J].石油勘探与开发，1998(5)：96-98.

[14] 赵良孝.对阿尔奇公式中m值物理、地质意义的重新认识[J].国外测井技术，2013(6)：21-23.

[15] 李欣,张志虎,李鸿儒,等.改进型阿尔奇方程在复杂岩性储层测井评价中的应用[J].石油工业技术监督，2015(12)：1-4.

[16] 刘忠华,吴淑琴,杜宝会,等.储层渗透性与地层因素关系的实验研究与分析[J].地球物理学报,2013(6):2088-2097.

[17] 张冲,郭聪,宋秋强,等.利用压汞资料预测储层地层因素F的改进方法[J].中国矿业大学学报,2016(4):747-753.

[18] 罗少成,成志刚,唐冰娥,等.致密砂岩储层胶结指数m和岩性系数a的研究[J].复杂油气藏,2014(4):1-5.

[19] 吴国海,郭海峰.变质岩储层变m值测井解释方法探索[J].国外测井技术,2015(4):36-40.

[20] 赵发展,王贇,何亿成.砾岩在不同矿化度下的岩电参数变化规律[J].物探与化探,2004(2):116-118.

(责任编辑何杰玲)

ApplicationofArchieformulaintheInterpretationofExtraLowPermeabilityReservoirAfterDeformation

TIAN Mi1， HOU Zhengmeng2， LI Zhandong1， HU Xiuquan3

(1.College of Petroleum Engineering Institute，Northeast Petroleum University，Daqing 163318，China； 2.Clausthal University of Technology， Deutschland，Clausthal 610065； 3.Fengcheng Oilfield Operation Area，PetroChina Xinjiang Oilfield Company， Karamay 834000， China)

The Archie formula has been widely used in the field of log saturation interpretation since it was put forward and has achieved remarkable results. It is the foundation of quantitative calculation of oil saturation with well log data. However, the experimental research is done under the indoor conditions of high porosity and high permeability rock sample，for the characteristics of low permeability reservoir, such as complex pore structure, high degree of cementation, and the difficulty in grasping the degree of pore tortuosity, using of Archie formula directly to calculate water saturation may make a larger error. The author madea large number of literature research, as well as the analysis of core data, deformed the Archie formula after introduced the permeability into the it, and finally established the Archie formula for extra-low permeability reservoir, and obtained the cementation index and conductivity of the extra-low permeability reservoir. In addition, the author discussed the influence of pore structure on rock electrical parameters and formation factors. This makes the Archie formula a widely use in the interpretation of logging reservoir saturation, and the calculation results of Archie’s in extra-low permeability reservoir more accurately.

extra low permeability; cementation index; archie formula; formation factor

2017-03-15

中国石油科技创新基金资助项目(2016D-5007-0212)；东北石油大学研究生创新基金资助项目“基于拟海底反射层条件水合物有效开发方式研究”

田秘(1989—)，女，硕士研究生，主要从事油藏描述方面的研究，E-mail:1014377995@qq.com； 通讯作者 李占东(1979—)，男，博士后，副教授，主要从事油藏描述方面的研究，E-mail:13644593771@163.com。

田秘，侯正猛，李占东，等.变形后阿尔奇公式在特低渗储层解释中的应用[J].重庆理工大学学报(自然科学)，2017(10):128-133.

formatTIAN Mi，HOU Zhengmeng，LI Zhandong,et al.Application of Archie formula in the Interpretation of Extra Low Permeability Reservoir After Deformation[J].Journal of Chongqing University of Technology(Natural Science)，2017(10):128-133.

10.3969/j.issn.1674-8425(z).2017.10.021

P631.84

A

1674-8425(2017)10-0128-06