大规模单点基础激励随机振动分析及并行计算

范宣华,于晨阳，王柯颖，方 叶，肖世富

(中国工程物理研究院 总体工程研究所， 四川 绵阳 621900)

大规模单点基础激励随机振动分析及并行计算

范宣华,于晨阳，王柯颖，方 叶，肖世富

(中国工程物理研究院 总体工程研究所， 四川 绵阳 621900)

基础激励作用下的随机振动分析为结构动力学有限元计算中的一种主要分析类型，在实际结构分析中得到了广泛应用。基于模态叠加法，对基础运动激励下的随机振动核心算法理论进行了系统推导。基于JAUMIN框架并行数据结构，在PANDA平台下完成了大规模算法设计和并行程序研发。结合数值算例对随机振动响应分析模块进行了对比验证和大规模并行可扩展性测试。研究结果表明：所研发的随机振动分析软件与商业软件的计算结果完全吻合，在并行求解能力上可达到上亿自由度、上万核，远超出商业有限元软件的计算水平。

单点基础激励；并行计算；随机振动；PANDA平台；并行可扩展性；模态叠加法

随机振动是自然界和工程结构分析中常见的一类振动。诸如大型建筑物因地震、车辆因路面不平等引起的振动都属于随机振动分析的范畴。随机振动不同于其他确定性振动，通常没有固定周期，无法用确定性函数进行描述，但具有一定的统计规律，一般可以用功率谱密度等统计量进行描述[1]。

大型复杂装备或建筑物经常会受到来自约束部位的一致基础激励作用，有限元随机振动分析多以平稳随机振动为前提，主要采用功率谱密度对结构的响应进行描述[2]。在目前的商业有限元软件中，串行分析求解能力基本维持在百万至数百万自由度量级，即便是国内部分开放的商业有限元并行软件，受技术禁运(开放核数最多在数百个以内，而且价格异常昂贵)和多年来串行编程机制下形成的内核影响，仅计算规模略有增加，但并行性能往往难以提升，极大制约了复杂结构的精细数值模拟水平[3]。

并行计算是解决这类大规模有限元问题的一个重要途径。作为近20年来随着计算机硬件快速发展而形成的一个热门研究方向，并行计算对提升计算分析的规模和精度、缩短数值模拟时间具有重要意义。本文以单点基础激励随机振动分析为研究对象，对基于自主并行软件平台PANDA[4]的大规模有限元并行计算研究进行介绍，以期为大规模精细有限元分析提供借鉴。

1 基础激励随机振动理论

随机振动分析的输入一般为作用于结构约束部位的载荷功率谱密度曲线，载荷可以是位移、速度、加速度等基础激励。本文从最为常用的基础加速度激励入手，对随机振动的核心理论进行推导。

随机振动算法理论的核心就是推导基础激励自功率谱密度与结构关注点自功率谱密度响应之间的传递关系。对于基础运动情形，以结构和地基的相对位移xr作为变量，可建立如下多自由度系统的运动方程：

(1)

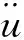
式(1)中xr为各节点自由度对应的相对位移向量，与绝对位移x以及基础运动位移u之间满足如下关系：

x=xr+du

(2)

对于运动方程(1)，采用模态叠加法[5]进行方程解耦。首先进行模态分析，与式(1)对应的广义特征值方程为

Mφ=ω2Kφ

(3)

i=1,2,…,m

(4)

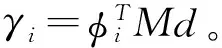
对于式(4)，在频域内的稳态解可以写为

(5)

其中Hi(ω)为第i阶模态对应的频响函数，即

(6)

对于平稳随机振动，根据功率谱密度定义，相应的模态功率谱密度可以表示为：

(7)

式(7)给出了基础运动加速度激励自谱密度和模态功率谱密度之间的递推关系。根据相对位移和模态位移的关系，可以得到有限元模型中第k个自由度相对位移功率谱密度Sxrkxrk和基础激励加速功率谱密度之间的关系：

φikφjkSηiηj=

(8)

其中φik为第i阶振型在第k个自由度处的取值，上标*表示共轭。结合虚拟激励法[6]思想，可对式(8)做进一步简化，得到

(9)

再根据相对位移和绝对位移的关系表达式(2)，得到第k个自由度的绝对位移自功率谱密度：

(10)

式中dk为方向向量d在第k个自由度处的取值。式(9)(10)分别给出了第k个自由度相对位移和绝对位移自功率谱密度与基础加速度激励自功率谱密度之间的递推表达式。根据求解得到的位移自谱密度，可以直接得到速度和加速度自功率谱密度，三者之间满足如下转换关系：

(11)

2 算法设计

根据本文的讨论和理论推导，可以建立如下单点基础加速度激励作用下的随机振动分析算法：

算法1 基础加速度激励单点随机振动分析算法输入:结构有限元模型,模态分析阶数m,模态阻尼比ξi,加速度激励功率谱密度曲线S¨u¨u(ω),激励方向;输出:指定节点自由度的位移、速度或加速度功率谱密度。1.根据结构有限元模型,在JAUMIN框架下进行离散,并行生成分布式质量矩阵M和刚度矩阵K;2.根据质量矩阵和刚度矩阵构造广义特征值问题,进行模态分析,获取的前m阶特征对(ωi,ϕi);3.根据基础运动作用方向在所有非约束自由度上构造单位方向向量d;4.结合整体质量矩阵、振型和方向向量求解基础激励对应的各阶模态参与系数;5.以指定计算的节点自由度作为第一重循环,以加速度输入自谱曲线离散后的频率作为第二重循环: a.获取每个计算自由度在各阶模态振型中的取值和对应方向向量中的值; b.计算模态坐标系下的各阶频响函数Hi(ω)(式(6)); c.按照式(9)和式(10)进行模态叠加,分别计算相对位移和绝对位移功率谱密度曲线; d.根据需要按照式(11)分别计算速度和加速度的自谱密度曲线。6.功率谱密度曲线计算结果输出。

在以上算法设计中，基础激励输入可以是位移或速度的功率谱密度曲线，三者输入之间同样满足式(11)的换算关系。此外，总体质量矩阵和刚度矩阵的生成、模态分析过程、响应求解等多个环节均可借助JAUMIN框架和PANDA平台进行并行求解。

3 并行实现

3.1 JAUNMIN框架和PANDA平台

以上单点基础激励随机振动的并行实现主要借助中国工程物理研究院自主研发的JAUMIN并行计算框架[7]和PANDA平台实现。JAUMIN是根据超大机群硬件结构特点面向大规模非结构网格计算而研发的并行计算框架，提供基本的底层并行数据结构和矩阵向量操作等数学运算，负责不同数据块之间的并行通信和数据管理等操作，同时为各类应用软件提供各类接口。有关JAUMIN的详细介绍参见文献[7]。

PANDA是笔者团队基于JAUMIN框架并行数据结构研发的结构力学有限元并行分析软件平台。PANDA平台基本架构以及与JAUMIN框架之间的关系如图1所示。

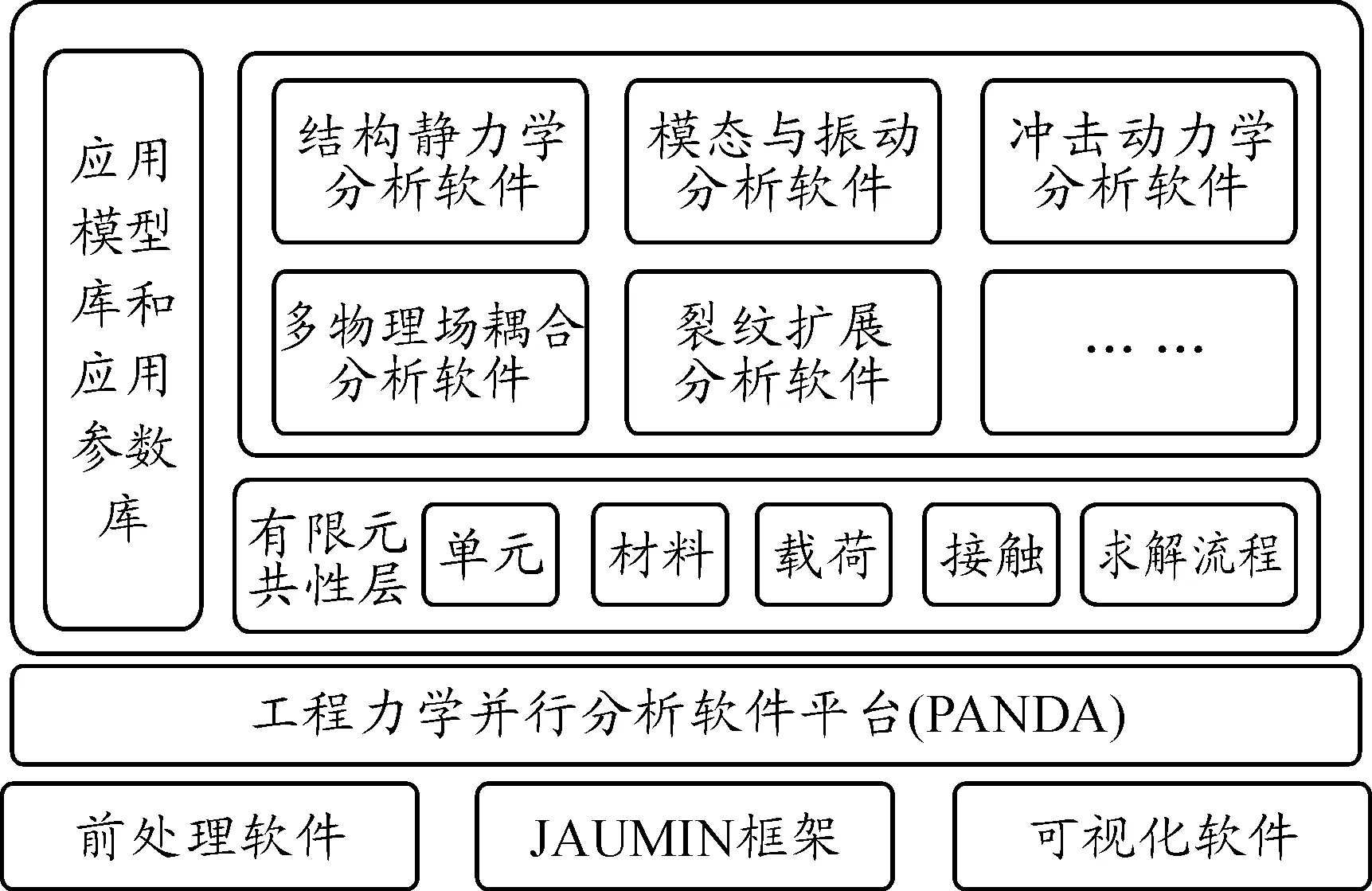
图1 PANDA平台的基本结构

目前整个PANDA平台包括静力学、模态和振动、冲击动力学、多物理场耦合分析等多个有限元分析模块，主要采用 C++ 和MPI编写语言，包含代码10万余行。对于复杂工程结构，JAUMIN框架结合前后处理软件完成结构的有限元建模和网格区域分解，PANDA平台根据结构材料属性和外载荷条件等完成矩阵并行组装和求解。单点基础激励随机振动分析只是模态和振动分析软件中的一个基本分析类型，此外还包含模态分析、地震响应谱分析、谐响应分析以及多点随机振动分析等多个动力学分析类型。

3.2 并行实现概述

首先，根据工程结构特点建立结构有限元模型。在基于JAUMIN框架的并行计算中，多采用自主前处理软件Supermesh进行建模，此外也支持商业有限元软件建模方式。对于建立的有限元模型，JAUMIN框架采用图剖分功能，将有限元网格进行区域分解，分成多个子区域。在区域分解时综合应用负载平衡技术，将有限元模型网格信息均匀分配到各个CPU计算节点，在各个CPU内，PANDA平台将结合模型本构和材料、边界等物理参数，并行生成分布式质量矩阵和刚度矩阵。

其次，利用生成的质量矩阵和刚度矩阵，PANDA平台调用模态分析模块进行模态分析并行计算，获取模态叠加所需的固有频率和模态振型等。模态分析在整个动力学分析过程中是最耗时间和资源的环节，其计算能力也基本决定了后续振动分析的计算能力。由于已经在PANDA平台下进行了相应并行求解的集成实现，故目前支持Krylov-Schur算法[8]和Jacobi-Davidson算法[9]等开展大规模模态分析并行求解[4,10]。

再次，根据模态分析计算结果，结合JAUMIN框架提供的矩阵向量等并行操作运算，获取各阶模态参与系数。

最后，将模态参与系数、计算自由度对应的各阶振型值、模态固有频率和模态阻尼比等作为响应计算输入，设计相应的模态叠加C++类，完成从基础激励到结构计算自由度直接频响函数的求解，并按照式(9)(10)设计随机振动分析C++类，实现相对位移和绝对位移自功率谱密度曲线的求解和计算结果输出。

除矩阵组装和模态分析阶段的并行环节以外，在随机振动分析实现中的并行环节主要有2个：① 求解模态参与系数; ② 计算各自由度的自谱密度曲线。在求解模态参与系数时，主要借助模态分析的质量矩阵以及模态振型在各个进程的分布式数据进行并行求解，而在计算各个节点自由度的自功率谱密度时，其计算过程是一个天然并行模式，每个CPU进程只负责本进程内节点自由度的自功率谱密度计算，相邻进程之间不需要任何数据通信。

4 数值算例

为验证研发模块的正确性和并行可扩展性，本节以光机靶球随机振动分析作为算例开展并行计算研究。光机靶球的有限元模型如图2所示。采用四面体单元进行划分，初始模型自由度数为340万，模态分析提取前100阶模态，采用Jacobi-Davidson算法求解，各阶模态阻尼比取0.01，在支架4个脚底施加沿水平方向的基础加速度激励，激励曲线为0～50 Hz范围内的白直谱(加速度功率谱密度为1(m/s2)2/Hz的直线谱)。计算靶球上方杆件最上端的水平方向的位移功率谱密度。

图2 光机靶球有限元模型

对于340万自由度初始模型，采用商业有限元软件ANSYS进行对比验证，ANSYS和PANDA计算得到的前100阶固有频率保持小数点后3位有效数字一致。图3给出了靶球顶端关注点的绝对位移功率谱密度对比情况，可以看出，ANSYS和PANDA计算得到的功率谱密度曲线几乎完全重合，验证了PANDA单点基础激励程序模块的正确性。

为进一步验证PANDA单点激励随机振动分析的并行可扩展性，在百万亿次大型机群上对靶球340万自由度模型进行了自适应网格加密后的随机振动计算，经过1次网格自适应加密后达到 1 700 万自由度，经过2次加密后达到1.3亿自由度。对于如此上千万乃至上亿自由度的有限元模型，已超出国内通用商业有限元软件的计算能力，目前只能借助并行计算软件完成。

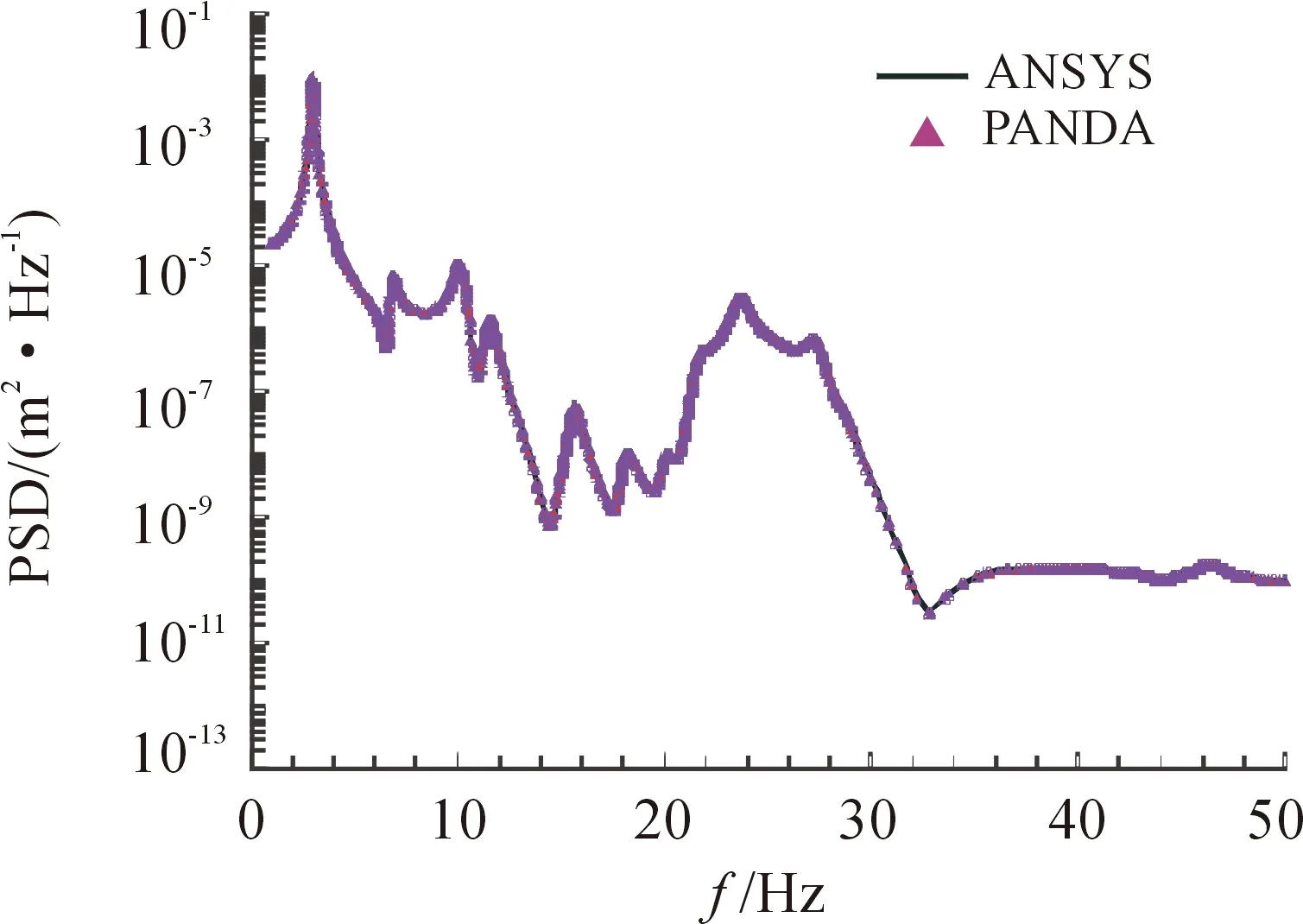
图3 绝对位移自功率谱密度曲线对比

对于靶球模型加密一次后得到的1 700万自由度规模，CPU核数从64个一直测试到 8 192个，得到不同并行CPU核数上的并行计算时间和并行效率，如表1所示。可以看出：对于该计算规模，在8 192核内，随着核数的增加，计算时间持续下降，并未出现计算拐点。8 192核相对于64核的并行效率为24%，说明PANDA平台下的单点随机振动程序具有优异的并行可扩展性。

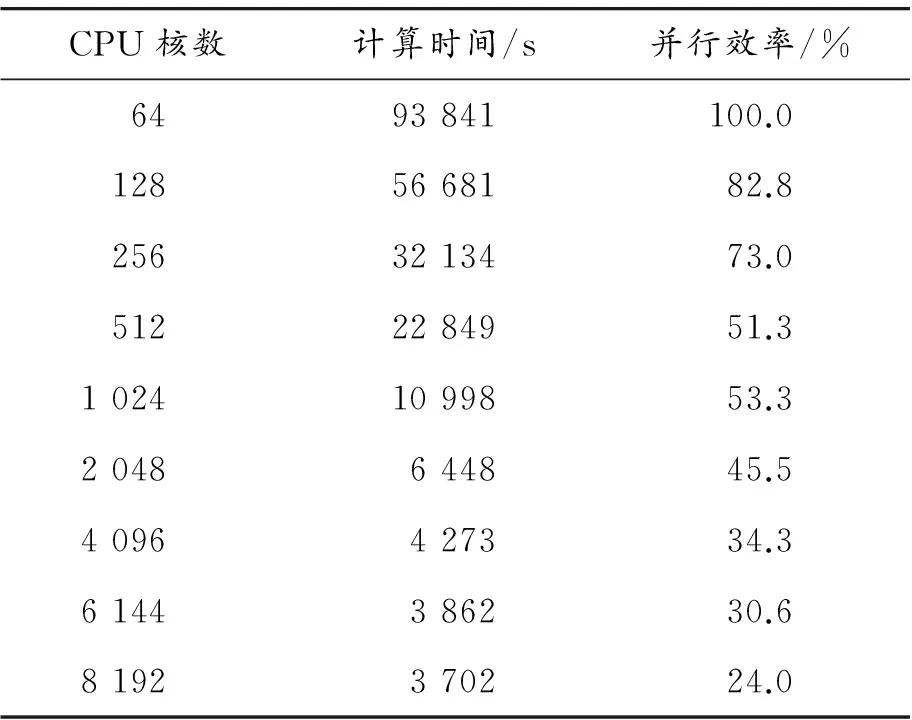
表1 靶球1 700万自由度模型随机振动分析计算时间和并行效率

对于加密2次得到的1.3亿自由度规模，分别进行1 024核、2 048核、4 096核、8 192核以及10 000核的并行可扩展性测试，均成功算出。相应计算时间情况如表2所示。可以看出：在 8 192核内随着核数的增加，计算时间近乎线性减少，8 192核较1 024核的并行效率提高达84%，表现出非常优异的并行可扩展性；超过8 192核后，由于大型机群系统自身网络分组配置原因导致跨域并行通信，并行效率有所下降，出现计算拐点，但万核级相对于千核级并行效率仍高达60%以上。为了更直观地表示分析模块的并行可扩展性，绘制1 700万自由度和1.3亿自由度的并行加速比曲线，如图4所示。

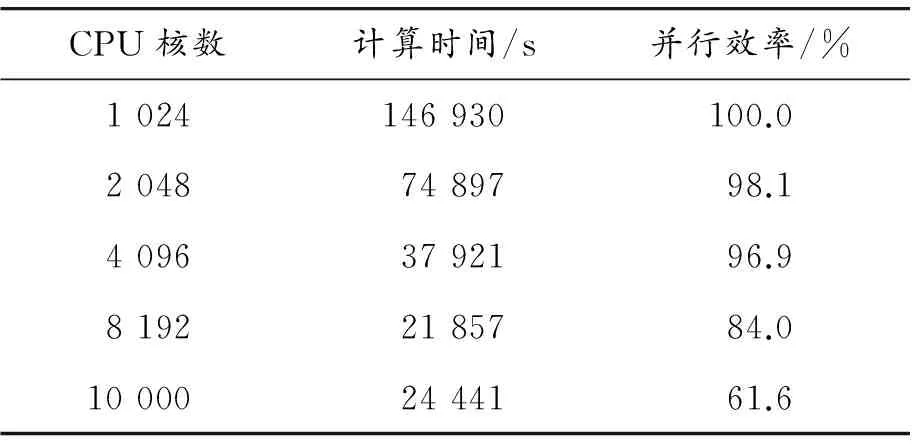
表2 靶球1.3亿自由度模型随机振动分析计算时间和并行效率

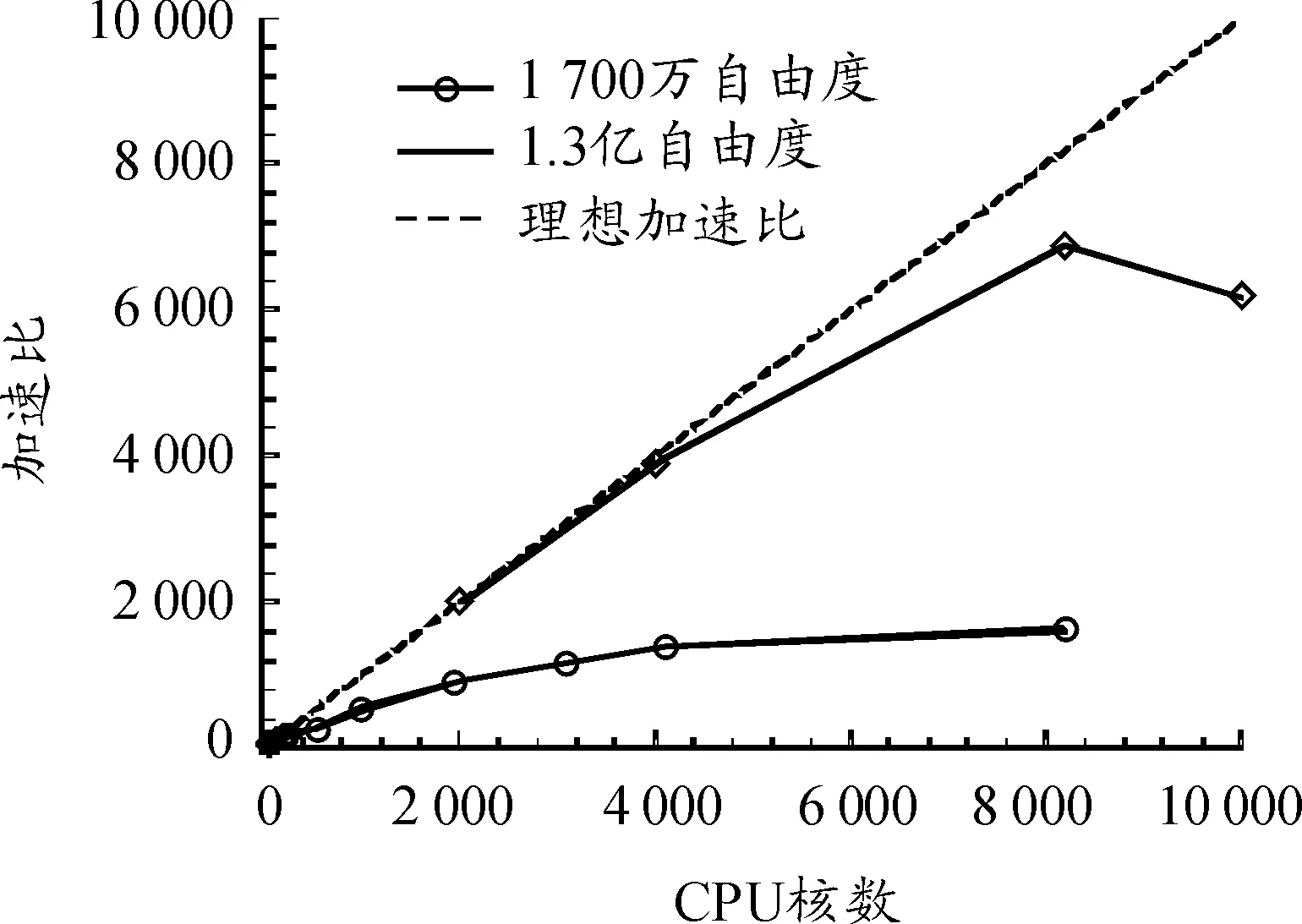
图4 两种规模的计算加速比曲线

从表1～ 2以及图4可以看出：

1) 计算规模越大，PANDA随机振动分析功能模块的并行可扩展性越优异。这主要是因为随着模型的增大，每个节点计算区域内的计算自由度数较边界通信部分的自由度数大大增加，通信带来的计算量相对变小。同理，对于同一计算规模，随CPU核数的增加，各区域带来的并行通信量增大，并行效率也逐渐下降。

2) 对于光机靶球之类复杂的算例，千万自由度计算时间从64核的26 h减少到8 192核的1 h左右。上亿自由度规模从1 024核的40余h减少到上万核的6 h左右。这相对于串行计算而言是几乎无法实现的，并行计算则不但大幅提升了计算规模，还大大缩短了数值模拟的计算时间，凸显了并行计算的优越性；

3) 本文的数值算例表明随机振动分析模块具备“上亿自由度、上万核”的并行可扩展能力。

5 结束语

本文基于模态叠加法，利用中国工程物理研究院自主研发的JAUMIN框架和PANDA平台，对单点基础激励随机振动分析进行了算法设计和并行实现，结合光机靶球数值算例验证了随机振动分析模块的正确性和并行可扩展性，取得了商业有限元分析软件无法达到的大规模并行计算能力。

本文研发的单点基础激励随机振动分析模块仅是PANDA平台下模态和振动分析软件中的一个基本分析模块，旨在说明基于JAUMIN框架研发的PANDA平台具有超强的并行可扩展性。在单点激励基础上，笔者所在团队近期已将随机振动分析从单点分析扩展到了多点激励分析，并将分析规模进一步提升到了10亿自由度以上，限于篇幅，在此不做深入介绍。

[1] CHRISTIAN L..Random Vibration:Mechanical Vibration and Shock Analysis[C]//3rdedition.Published in Great Britain and the United States by ISTE Ltd and John Wiley & Sons,2014.

[2] CHOPRA A K.Dynamics of Structures-Theory and Applications to Earthquake Engineering[M]//4th edition.New Jersey:Prentice Hall,2012.

[3] FAN X,WANG K,XIAO S,et al.Some progress on parallel modal and vibration analysis using the JAUMIN framework[J].Mathematical Problems in Engineering,2015(2):1-8.

[4] 范宣华.基于Panda框架的大规模有限元模态分析并行计算及应用[D].北京：北京大学,2013.

[5] ITOH T.Damped vibration mode superposition method for dynamic response analysis[J].Earthquake Engineering & Structure dynamics,1973,2(1):47-57.

[6] 林家浩，张亚辉.随机振动的虚拟激励法[M].北京：科学出版社,2006.

[7] LIU Q K,ZHAO W B,CHENG J,et al.A programming framework for large scale numerical simulations on unstructured mesh[C]//IEEE 2nd International Conference on High Performance and Smart Computing.New York:[s.n.]， 2016:310-315.

[8] STEWART G W.A Krylov-Schur algorithm for large eigenproblems[J].SIAM Journal on Matrix Analysis and Applications,2001,23(3):601-614.

[9] SLEIJPEN G L G，VORST H A V.A Jacobi-Davidson iteration method for linear eigenvalue problems[J].SIAM Journal on Matrix Analysis and Applications,1996,17(2):401- 425.

[10] FAN X H,CHEN P,WU R,et al.Parallel computing study for the large-scale generalized eigenvalue problems in modal analysis[J].Science China Physics,Mechanics and Astronomy,2014,57(3):477- 489.

(责任编辑杨黎丽)

ParallelComputationofLarge-ScaleRandomVibrationAnalysisUnderSingle-PointMotion-BasedExcitation

FAN Xuanhua， YU Chenyang, WANG Keying, FANG Ye, XIAO Shifu

(Institute of Systems Engineering, China Academy of Engineering Physics, Mianyang 621900, China)

The random vibration analysis under the basic excitation is a kind of main analysis type in the finite element calculation of structural dynamics, and it has been widely used in practical structural analysis. Based on the modal superposition method, the random vibration algorithm theories under the basic motion excitation were systematically deduces. Based on the parallel data structure of JAUMIN framework, large-scale algorithm design and parallel program development were carried out under the PANDA platform. Numerical examples are given to verify the rightness as well as the large-scale parallel scalabilities of the random vibration response analysis. The results show that the random vibration analysis software developed by us is in good agreement with the calculated results of commercial software, and can reach hundreds of millions of degrees of freedom, tens of thousands of CPU cores in the parallel solution scalability, going far beyond the calculation level of commercial finite element software.

single-point base excitation; parallel computation; random vibration; PANDA platform; parallel scalability; mode superposition method

2017-06-21

国家自然科学基金面上资助项目(11472256)；科技部“高性能计算”重大专项课题(2016YFB0201005)；国防基础科研计划项目(C1520110002)；中国工程物理研究院院长基金、院发展基金和双百人才基金资助项目(YZ2015011，2014B0202025，ZX04003)

范宣华(1981—),男,山东日照人,博士,研究员,主要从事结构动力学并行计算研究,E-mail：fanxh@caep.cn。

范宣华,于晨阳，王柯颖，等.大规模单点基础激励随机振动分析及并行计算[J].重庆理工大学学报(自然科学)，2017(10):56-61,89.

formatFAN Xuanhua，YU Chenyang, WANG Keying, et al.Parallel Computation of Large-Scale Random Vibration Analysis Under Single-Point Motion-Based Excitation[J].Journal of Chongqing University of Technology(Natural Science)，2017(10):56-61,89.

10.3969/j.issn.1674-8425(z).2017.10.009

TB132

A

1674-8425(2017)10-0056-06