地铁运行区域新建建筑全过程实测与数值模拟
钟才敏, 马人乐, 吴学淑
(1.同济大学 建筑工程系,上海 200092; 2.中国建筑设计院上海中森建筑与工程设计顾问有限公司,上海 200120)
地铁运行区域新建建筑全过程实测与数值模拟
钟才敏1,2, 马人乐1, 吴学淑2
(1.同济大学 建筑工程系,上海 200092; 2.中国建筑设计院上海中森建筑与工程设计顾问有限公司,上海 200120)
以邻近地铁线路的某新建建筑为例,对从项目动工至建筑封顶过程中的主要节点进行全过程实测,得到地铁经过时自由场地及施工不同阶段建筑内部各楼层的振动数据。建立单体的有限元模型,采用不同的激励输入方式进行数值模拟,并将计算结果与实测结果进行对比验证,以获取既有地铁运行区域拟建建筑施工前振动预测的有效方法。在数值分析过程中,针对环境振动,提出了“原位激励”的概念。分析结果表明:一致激励输入仅适用于建筑平面尺寸较小时进行初步预测;原位激励与多点激励的输入方式计算结果准确可靠,可满足设计各个阶段的振动预测需求;根据不同的需求可分别选择采用原位激励或多点激励的输入方式进行振动预测;采用自由场地实测结果作为输入激励进行振动预测时,可将计算结果根据不同的建筑类型进行修正。该研究成果可对既有地铁运行区域拟建建筑施工前进行振动评价提供参考。
地铁振动;数值模拟;原位激励;多点激励;振动预测
近年来,轨道交通在我国得到迅猛发展。轨道交通给人们带来便利的同时,其运行引起的环境污染问题也日益引起关注,特别是地下线路(地铁)的振动污染已成为城市环境影响的主要问题之一[1]。在上海等大城市,轨道交通的运行线路已从原有的市区扩展到郊区。同时,由于城市土地短缺以及前期规划的不合理,越来越多的新建筑在既有地铁运行区域建造,从而对邻近地铁运行区域拟建建筑施工前的振动预测提出了迫切需求。
地铁运行引起的场地及周边建筑物振动是一个复杂的系统问题,包括了振源、传播途径及受振体三个方面。对于这个问题主要有四种研究方法,即解析法、现场实测法、经验预测法和数值模拟法[2]。目前,在项目前期,国内外对地铁运行区域拟建建筑的振动预测主要采用经验预测法[3-4]。我国在实际实施时主要依据环评部门的环评报告,但是由于轨道交通振动预测目前尚无成熟、通用的预测模式,且受环评部门自身专业及实际工程经验等因素的局限,大多很难将振动的污染情况进行准确、全面的分析。以有限元方法为主的数值模拟方法在近几十年来得到快速发展并在轨道交通领域得以应用。王田友等[5-6]建立拟建建筑有限元模型,采用场地实测数据作为输入激励进行振动预测;马蒙等[7]采用实测获取已有建筑场地外的地铁振动数据作为输入激励,建立建筑模型进行数值分析。有限元法可方便的模拟环境振动的各个系统,但该方法采用了各种程度的假设,模拟计算结果的准确性需要相应的实测验证。由于场地及建筑物实测受诸多因素的影响,且需要进行大量的重复试验,周期长,耗费大,因而已有研究成果大多仅基于对施工前自由场地或已建成建筑的阶段性实测,而针对同一新建建筑从施工前的自由场地至结构封顶进行全过程实测并建立有限元模型进行对比验证则几乎未涉及。
本文针对已投入运营的上海地铁7号线附近的某新建医院建筑进行全过程实测,同时建立该建筑的有限元模型进行数值模拟,并将计算结果与实测结果进行对比验证,以探讨适用于既有地铁运行区域拟建建筑振动预测的数值分析方法。
1 拟建建筑物概况与测试结果
拟建医院由4幢单体建筑组成,布置于地铁沿线两侧。为获取地铁运行引起的建筑物振动数据,在施工过程中对位于地铁同侧的行政楼与住院楼进行了实测,建筑物与地铁关系及测点布置如图1所示。
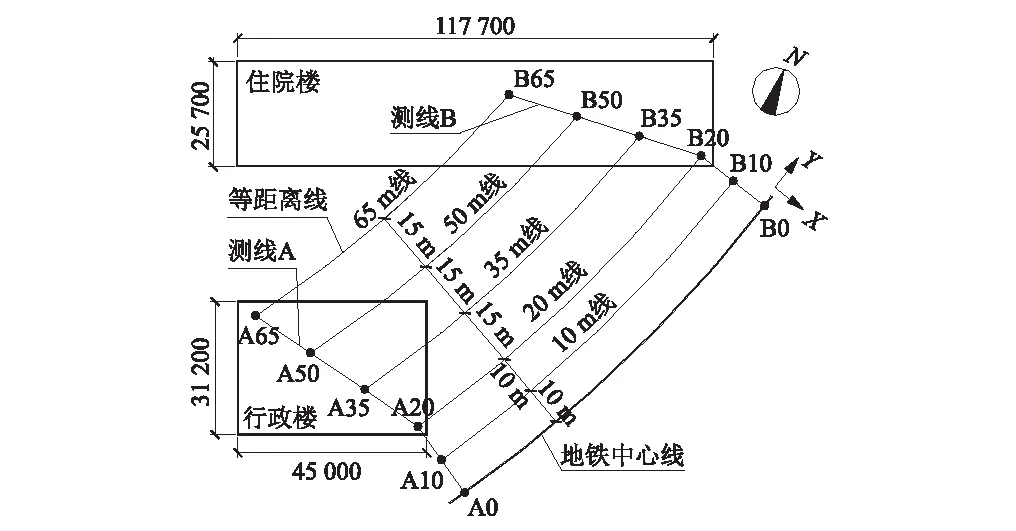
图1 测线与测点布置示意图Fig.1 Layout of test lines and points
行政楼为现浇钢筋混凝土框架结构,建筑面积5 850 m2,地上4层,无地下室,结构外边线与地铁隧道最近距离为15.42 m;住院楼为现浇钢筋混凝土框架-剪力墙结构,建筑面积40 600 m2,地下1层,地上13层,结构外边线与地铁隧道最近距离为13.84 m。根据建筑物情况,布置了A、B两条测线,每条测线在建筑物投影范围内布置4个测点,建筑与地铁之间布置2个测点。测点与地铁隧道中心的水平距离分别为0 m、10 m、20 m、35 m、50 m和65 m,并据此对测点进行命名(如A35即为A测线距离隧道中心35 m的测点)。每个测点同时测试3个方向的振动(Z为竖向、Y为顺隧道水平方向、X为垂直隧道水平方向)。根据已有研究,Z向振动对人体影响最大[8],因而文中分析主要考虑Z向振动。
测量仪器采用Lance LC0132T高灵敏度压电式加速度传感器,传感器灵敏度系数为42 V/g,分辨率为2 μg。采用同济大学开发的SVSA 软件进行数据采集,采样频率为200 Hz。为获取地铁运行引起对拟建建筑物全过程的振动时程,进行现场实测的时间需根据工程进度进行。整个工程的施工,从场地平整至建筑物封顶,历时近三年。为保证测试结果的有效性,每个测点测试次数不少于5次。同时,各次测试均在一天中的相同时段进行,以减少不同时段地铁的不同运行状况带来的影响。本文所涉及的测试工况如表1所示。
现场实测得到的是测点在地铁经过时的加速度时程。为方便比较,本文将加速度时程换算为加速度有效值以及计权振动加速度级[9],以测点强度形式对各点进行比较。采用加速度有效值描述的行政楼与住院楼在各工况下测点的振动情况如表2、表3所示。

表1 测线A、测线B测试工况与测点位置Tab.1 Test conditions and locations of line A and line B
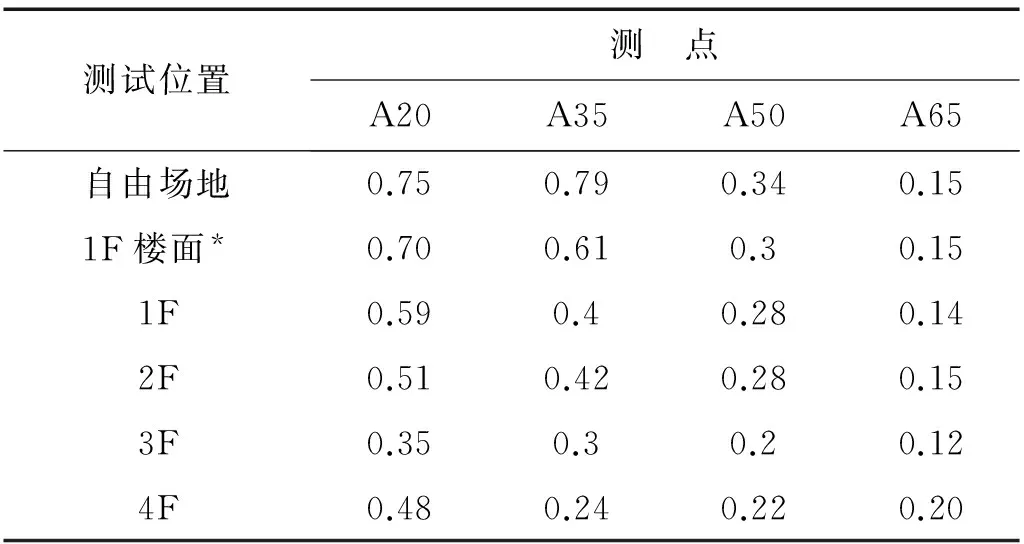
表2 行政楼实测加速度有效值Tab.2 Field test root mean square value of accelerationof administration building gal

表3 住院楼实测加速度有效值Tab.3 Field test root mean square value of accelerationof inpatient building gal
2 环境振动问题的有限元法
地铁运行引起的环境振动问题,常规的分析方法是建立隧道-土层-建筑物完整模型,并将地铁运行产生振动施加到轨道结构上进行分析。对于既有地铁运行区域,新建建筑只能建在地铁线路外侧的一定距离之外,且施工时对已有线路的影响有严格要求;其次,既有地铁运行区域地铁已经开通,可方便的测得地铁经过建设场地时地面的加速度时程,因而可参照建筑物抗震的计算方法,即直接建立上部结构三维刚性地基模型,并将地铁经过时的实测自由场地加速度时程作为激励输入到建筑物底部进行计算分析。
对于环境振动,求解动力有限元方程的方法与抗震时有所不同。动力有限元常微分方程的常用解法可分为两类:直接积分法和振型叠加法。建筑结构设计时,一般采用振型叠加法来计算地震作用。地铁运行所引起的场地振动与地震波相比有很大的差异。在振动强度方面,地铁引起的场地振动波远小于地震波;从频谱来看,地震波的卓越频率在2~3 Hz之间,而地铁引起的场地振动波卓越频率在50~80 Hz之间。对于具有高频特性的环境振动,应采用直接积分法进行计算。
由于地铁引起振动的高频特性,模拟地铁振动时需要考虑较宽的频带。计算分析采用Rayleigh阻尼,取较高频率振型的阻尼比用以确定阻尼常数,以避免高频振型反应由于高阻尼被消除[10]。数值模拟时对频率为5 Hz与80 Hz所对应振型的阻尼比取为0.03来确定其他振型的阻尼比。
在动力荷载作用下工程结构的反应分析实质是一个波动问题。计算时需要使得有限元单元尺寸和波长之比足够小,这样波动的数值模拟才具有一定的精度[11]。对于环境振动,根据波长可将单元的最大尺寸控制在2.0~3.0 m[12]。
计算时时间步长的选择是另一个重要因素。在选择时间步长时,不仅需要考虑解的精度,还需要考虑解的收敛性以及稳定性。对于环境振动,建议所取时间步长不小于输入激励所对应的时间步。
3 地铁运行引起建筑物振动的数值模拟
采用Sap2000通用有限元软件建立行政楼与住院楼三维有限元刚性地基模型。行政楼没有地下室,取地面所在位置(一层)作为计算模型的底部。住院楼有一层地下室,采用数值方法进行环境振动分析时,可不考虑地下室的影响,而仅对上部结构建立有限元模型进行分析[13],因而住院楼也以一层作为三维模型的底部。两个单体的三维计算模型,如图2所示。

图2 数值模拟三维计算模型Fig.2 3D calculation model of numerical simulation
3.1 数值模拟的输入激励
项目实测时获取了自由场地、施工完一层楼板时的一层楼面以及结构封顶后的一层楼面加速度时程(见表1)。测点在三种工况中所处的空间位置基本一致,均在建筑物底部,但处于项目建设的不同阶段,因而振动存在一定的差异。将这三组实测获取的加速度时程转化为加速度有效值(见表2、表3),并将结果绘入同一图中以比较不同工况测点强度变化,如图3所示。
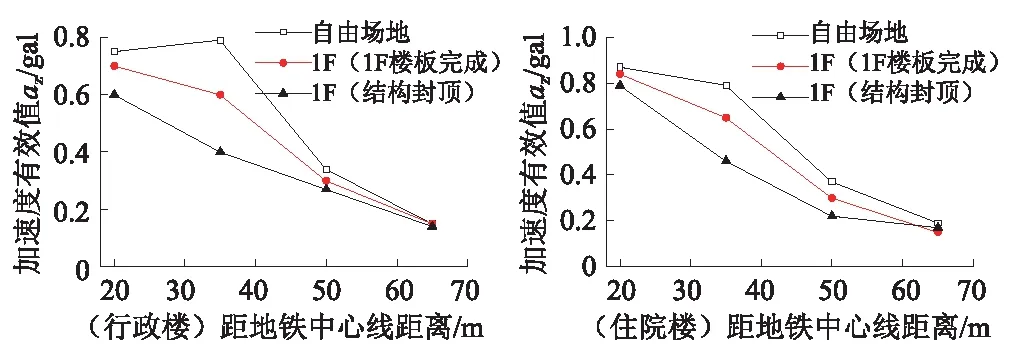
图3 自由场地与一层楼面实测结果对比Fig.3 Comparison of test results of free field and 1st floor
从图3可知,距离地铁隧道中心不大于50 m的测点,自由场地时实测的振动强度最大,施工完一层楼板时的一层楼面次之,结构封顶后的一层楼面振动强度最小。造成这个结果的原因如下:自由场地测试时尚无建筑物,振动强度只与振源强度、与振源的距离以及土层特性有关;一层楼板浇完后,楼面测点通过混凝土楼板形成了整体,各测点之间有一定的相互影响,振动波从土中传入混凝土楼板中时存在部分的能量损失,因而振动有所减弱;结构封顶后,上部建筑质量大、刚度好,振动波从自由场地传入建筑物进行能量转化时产生的能量损失较一层楼板完成时更大,从而减弱了振动强度。
采用三维刚性地基模型进行数值模拟时未考虑土层-建筑物的相互作用,有限元模型与结构封顶后的建筑一致,且模型底部与实际一层楼面位置相同。因而通过数值模拟方法与实测上部楼层结果进行对比验证时,采用结构封顶时一层楼面的实测加速度时程作为刚性地基模型的输入激励才是合适的,此时的激励与实际情况完全对应。本文后续章节对行政楼、住院楼进行数值模拟时,均采用结构封顶后的一层楼面实测时程作为输入激励。但对于既有地铁运行区域,需要在建筑物施工前进行振动预测时,只能获取自由场地的振动时程。由于将自由场地实测振动输入模型进行计算时无法考虑土层-建筑物相互作用产生的能量损失,将导致计算结果与实际情况存在一定的差异。该差异可通过对模型分别采用自由场地以及结构封顶后一层楼面实测时程作为输入激励的计算结果对比得到。在确定输入激励时,选择符合地铁时程特点的典型时程,同时所选时程的加速度有效值不小于该测点5次实测时程有效值的平均值。
3.2 行政楼数值模拟分析
对于地震波来说,只有在计算大跨结构时,才会考虑多点激励与行波效应。而对于地铁运行引起的环境振动,振动强度随着与地铁隧道距离的增大而迅速变化,导致建筑物中与地铁隧道距离不同的点接受到的振源输入强度差异非常大,因而计算时采用多点激励输入才是合适的。但由于采用多点激励计算的工作量较大,目前一致激励的输入方式仍被广泛采用。近些年部分研究已开始尝试采用多点激励来分析建筑物的响应[14]。但由于缺乏建筑物全过程实测数据进行验证,这些研究目前仅停留在理论计算阶段。尽管如此,由于一致激励输入所具有的计算速度优势以及更强的可操作性,采用一致激励进行环境振动研究仍具有重要的意义,特别是可以较好的满足项目方案设计阶段的需求。
3.2.1 一致激励输入计算分析
对于邻近地铁的拟建建筑,在项目的方案设计阶段,需要采用保守的计算方法对于地铁运行可能引起的建筑内振动情况进行预测。此时可采用一致激励的输入方式计算建筑物的振动响应。
对于行政楼,采用结构封顶后1层A20测点实测时程作为输入激励对三维模型进行分析,计算结果如表4所示。将表2中的实测数据与表4结果绘制在同一张图中,以比较实测结果与数值计算结果的差异,如图4所示。
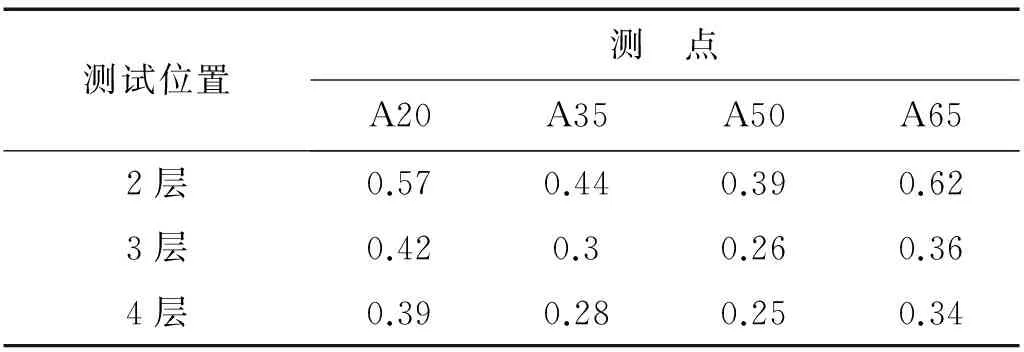
表4 行政楼一致激励输入时各楼层计算加速度有效值Tab.4 Caculated root mean square value of accelerationwith uniform excitation of administration building gal
从图4(a)、图4(b)可看出,由于输入激励为一层A20测点的实测时程, A20测点以及邻近的A35测点在二层与三层的计算结果与实测结果接近。另外也可看出,A35测点吻合度甚至要略高于A20测点。造成这个结果的主要原因在于引起实测振动的激励与计算时输入的激励不一致,从而产生一定的偏差;另一方面,一致激励的输入方式导致相同强度的振动从各竖向构件底部传到测试楼层,并在测点处振动叠加也对结果产生影响。A50与A65测点的计算结果均明显大于实测结果。这是由于输入激励的强度要远大于A50与A65测点的实际振源强度。如A65测点,其结构封顶后一层实测加速度有效值仅为0.14 gal,远小于作为一致激励输入的加速度有效值0.59 gal。图4(c)显示四层A65测点差异要小于二层以及三层,这是由于随着楼层的增加,实测振动响应逐步衰减,从而导致与计算结果的差异也逐渐变小。
从以上分析可知,采用一致激励输入对建筑物内振动响应进行初步预估时,将建筑内与地铁距离最近的测点实测时程作为输入激励进行计算是偏安全的,但如果其他测点实测数据有反弹,则应考虑振动反弹点对于建筑物的影响。对于多层建筑而言,采用一致激励输入时,作为输入激励测点的相邻范围(15 m以内)的计算结果与实测结果较为接近,可作为建筑平面布置的参考依据。建筑物内其他区域,尤其是较低楼层部位,计算结果将明显大于实际振动强度。
3.2.2 原位激励输入计算分析
“原位激励”是本文针对环境振动(文中为地铁运行引起的建筑物振动)特点所提出的一个概念。所谓“原位激励”,是指预测建筑物内由于地铁运行引起的振动时,对于建筑物内某楼层的特定区域,计算时采用该区域在地面投影内测点的实测加速度时程作为输入激励的计算方法。例如,需要了解行政楼三层距离地铁隧道50 m处房间的振动情况时,则选择自由场地A50测点实测加速度时程作为输入激励进行计算即可,但所得到的计算结果也仅适用于各楼层该测点所对应区域。“原位激励”实质上是一致激励的特殊输入方式,一次计算得到的结果仅对输入激励测点所对应的上部特定区域有效。要获取其他区域的振动响应时需要采用目标区域在地面投影范围内测点的实测时程重新输入进行计算。
根据“原位激励”的定义,将结构封顶后的一层各测点的实测加速度时程分别作为激励进行计算,每次取与输入激励测点所对应的上部楼层测点计算结果并最终进行汇总,得到整个建筑物的振动数据,结果见表5。将该表结果与实测结果(表2)绘图进行比较,如图5所示。从图中可看出,无论是数据的吻合度还是变化趋势,原位激励计算结果与实测结果均表现出较好的一致性,但部分测点还是有一定的差异,原因存在于以下几个方面:首先,上述计算结果均为某特定点原位激励输入时的振动响应,这个结果无法反应测点之间振动的相互影响;其次,计算时不同楼层的计算结果对应同一个输入激励,而实测时受人力及仪器限制,每次最多同时对一个楼层测点进行测试,因而不同楼层的实测结果是由不同列车运行引起的。尽管实测时对各测点进行了多次测量并取比较后的振动典型时程,但由于实测不可避免的受地铁列车运行参数(如载重、车速等)的影响,因而该结果与同一振源引起的振动相比必然存在一定的差异。

图4 行政楼实测结果与一致激励输入时计算结果对比Fig.4 Comparison of test results and calculated results with uniform excitation of administration building

图5 行政楼实测结果与原位激励输入计算结果对比Fig.5 Comparison of test results and calculated results with in situ excitation of administration building表5 行政楼原位激励输入各楼层计算加速度有效值Tab.5 Field test root mean square value of accelerationwith in situ excitation of administration building

gal
从以上分析可看出,采用原位激励可以得到较为准确的计算结果,且计算原理明确。进行局部范围振动预测时,计算过程简单,仅需输入所关注区域投影范围内测点的实测时程进行计算即可。在设计前期需要快速了解地铁运行对拟建建筑物特定区域的振动影响时,具有较好的可操作性。
3.2.3 多点激励输入计算分析
随着与振源距离的加大,地铁运行所引起的场地振动强度迅速衰减,这就导致建筑物内与振源不同距离的柱(墙)底部经历不同的运动。因而,在考虑地铁运行对建筑物的影响时,为获取更加精确的结果,有必要采用多点激励的输入方式。采用多点激励计算时按大质量法,采用Newmark直接积分法进行动力时程分析。同时输入结构封顶时一层楼面A20、A35、A50以及A65测点所测得的加速度时程进行计算。
采用多点激励输入的计算结果与实测结果对比如图6所示。从图中可看出,除个别测点外,多点激励的计算结果与实测结果的吻合度较高,说明采用多点激励的输入方式可取得较精确的结果。同时,图中各层均有个别测点计算结果与实测结果有一定的差异,这是因为实测时不同楼层测点所测得的是不同车次地铁产生的振动响应,从而导致实测结果存在不确定性。
对比三种不同的激励输入方式可看出:一致激励输入方式最为简单,但计算结果误差较大,仅适用于初步预估;对楼层局部位置进行振动预测时,原位激励输入方式计算过程简单,结果较为准确,而需要了解整个建筑物的振动情况时,需要进行多次计算,整个计算过程复杂;多点激励输入方式的计算过程较为复杂,但计算结果准确,且可以一次得到整个建筑物的振动数据。
3.2.4 自由场地与结构封顶后一层楼面实测时程分别作为输入激励的计算结果比较
为方便与实测结果进行验证,以上数值模拟采用了结构封顶后的一层楼面实测时程作为输入激励。但如需进行振动预测,施工前只能测得自由场地加速度时程。对于上部楼层,采用这两种实测时程作为输入激励进行计算是存在一定差异的。

图6 行政楼实测结果与多点激励输入计算结果对比Fig.6 Comparison of test results and calculated results with multi-support excitation of administration building
图7为分别采用这两种实测时程作为输入激励计算时上部楼层振动响应比较。从该图可以看出,总体来看,采用自由场地实测时程作为输入激励计算的各层振动响应要大于采用一层实测时程时的相应计算结果。其中,A35测点结果差异最大,各层差值均达到2 dB以上。这主要是因为A35测点的两种输入激励本身就有较大差异(见表2)。对于另外3个测点,两种不同激励下的计算结果振级差在1~2 dB。因而,从行政楼计算结果看,对于多层建筑的振动响应预测,采用自由场地实测时程作为输入激励进行计算时,可考虑将计算得到的振级修正-1~-2 dB。

图7 行政楼采用自由场地与一层实测波作为输入激励时振级对比Fig.7 Comparison of calculated vibration level when free field and first floor wave used as input excitation of administration building
3.3 住院楼数值模拟分析
住院楼与行政楼有较大的差异。从结构体系来说,住院楼是框架-剪力墙结构;从建筑高度来看,住院楼是高层建筑。另外,在平面尺度上,行政楼长度为45 m,而住院楼沿垂直地铁隧道方向长度达到近120 m,因而其对于微振动的反应特性与行政楼有很大的不同。
根据现场实测显示,住院楼内在距离地铁隧道中心80 m处振动强度已很弱,接近背景振动。对于住院楼内距离隧道中心大于80 m的区域,已没有必要考虑地铁运行引起的振动响应。因而对于这种尺度较大的建筑,采用一致激励的输入方式进行计算已没有实际意义。鉴于此,以下仅采用原位激励以及多点激励两种输入方式来分析住院楼的振动响应。
3.3.1 原位激励与多点激励输入的计算分析
采用原位激励的输入方式对住院楼进行振动分析时,在模型底部分4次分别输入结构封顶后的一层楼面B20、B35、B50与B65测点实测加速度时程,每次取输入测点所对应的上部楼层测点的计算结果,并将4次计算结果进行汇总后得到整个建筑物的振动响应。
采用多点激励的输入方式计算时,同时输入B20、B35、B50以及B65测点的实测时程进行计算,计算时参数取值与行政楼相同。多点激励的输入范围如图8所示。
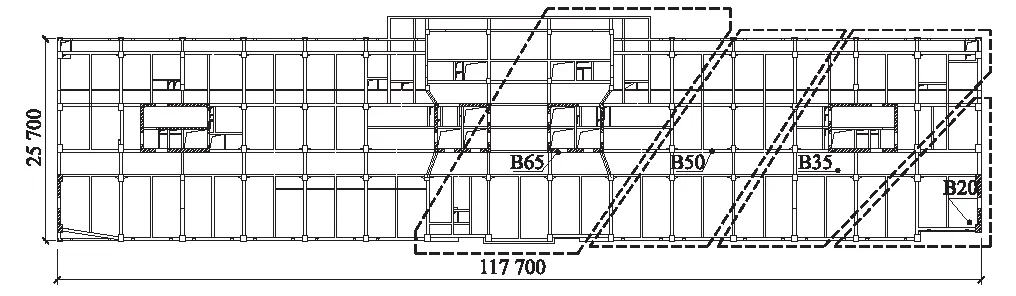
图8 住院楼多点激励的输入范围示意Fig.8 Layout of multi-support excitation input of inpatient building
将原位激励与多点激励的计算结果与实测结果进行对比,如图9所示。从图中可看出:首先,原位激励、多点激励的计算结果与实测结果整体上较为吻合,变化趋势也基本一致;其次,采用原位激励与多点激励两种输入方式的计算结果非常接近,采用多点激励输入方式的计算结果在大部分测点均比采用原位激励计算时略大。
根据以上分析可知,采用原位激励以及多点激励的输入方式进行环境振动预测均可达到较为理想的结果,但两种计算方法在输入方式的难易程度以及适用工况上有一定的差异。在输入方式上,采用原位激励输入时每次输入一个测点的激励进行计算,但需分别对每个作为激励的测点计算一次,并将每次计算结果汇总后才能获取整个建筑物的振动响应;采用多点激励输入时则需要将建筑物底部划分为不同的激励输入范围,对同一范围的柱(墙)底部输入同一激励,全部激励输入后同时进行计算,一次得到整个建筑的振动响应。因而,如果仅需对建筑物的特定区域进行振动预测,采用原位激励进行计算更为简单快捷;如果需要得到建筑物整体振动响应时,则采用多点激励更为方便。

图9 住院楼实测结果与原位激励、多点激励输入计算结果对比Fig.9 Comparison of test results and calculated results with in situ excitation and multi-support excitation of inpatient building
3.3.2 自由场地与结构封顶后一层楼面实测时程分别作为输入激励的计算结果比较
采用B20、B35、B50与B65测点在场地平整后自由场地的实测时程作为输入激励,获得上部结构的振动响应,并与采用结构封顶后一层楼面实测时程作为输入激励的计算结果进行对比,结果如图10所示。从图中可看出,对于四层B20、B35与B50测点,采用自由场地时程作为输入激励的计算结果比采用一层实测时程时大1~4 dB,而在B65测点结果较为接近;对于九层与十三层,50 m以内测点自由场地结果仍大于一层楼面实测输入时结果,但楼层越高,差值越小,九层差值在1~1.5 dB,而十三层差值仅为0~1 dB;B65测点在九层有一定的差异,十三层计算结果基本相同。因而,从住院楼计算结果看,采用自由场地的实测作为输入激励计算拟建高层建筑物的振动响应时,在距离地铁中心小于50 m的范围,中低楼层(如8~9层及以下)可对计算结果进行-1~-2dB的修正,而对于建筑其他部位,可不做调整。

图10 住院楼采用自由场地与一层实测波作为输入激励时计算振级对比Fig.10 Comparison of calculated vibration level when free field and first floor wave used as input excitation of inpatient building
4 结 论
本文针对既有地铁运行区域新建建筑进行了全过程实测,同时建立建筑物三维模型进行数值模拟,并将数值分析结果与实测结果进行对比验证,得到以下结论:
(1)采用数值模拟方法对地铁运行引起的建筑物振动进行分析时,一致激励输入方式仅适用于建筑平面尺寸较小时,在方案设计阶段做初步振动预测;原位激励与多点激励的输入方式较一致激励复杂,但计算结果准确,适用于各个阶段。
(2)需要获取建筑物内某特定区域的振动响应时,采用原位激励输入方式计算过程简单,结果较为准确;需要得到建筑物完整的振动响应时,则采用多点激励输入方式结果准确,且操作上更为方便。
(3)采用自由场地实测时程作为输入激励进行振动预测时,对于多层建筑(如行政楼),可将上部楼层计算结果进行修正,修正值取-1~-2 dB;对于高层建筑(如住院楼),在距离地铁50 m的范围内,对于中低区(8~9层及以下)可对计算结果进行-1~-2 dB的修正。由于以上修正值仅为本案例的分析结果,该结论的普适性还需更多的实测案例进行验证。
[1] 辜小安. 城市轨道交通环境影响评价中地下线路振动源强取值存在的问题与建议[J]. 铁路节能环保与安全卫生,2013, 3(5): 211-216.
GU Xiao’an. The suggestions and the problems of the vibration source intensity data of the underground line in the environmental impact assessment of the urban rail transit[J]. Railway Occupational Safety Health & Environmental Protection, 2013, 3(5): 211-216.
[2] 夏禾. 交通环境振动[M]. 北京: 科学出版社, 2010.
[3] 环境影响评价技术导则——城市轨道交通:HJ 453—2008[S]. 北京: 中国环境科学出版社, 2009.
[4] Transit noise and vibration impact assessment: TA-VA-90-1003-06[S]. Washington DC: Office of Planning and Environment Federal Transit Administration, 2006.
[5] 王田友. 地铁运行所致环境振动与建筑物隔振方法研究[D]. 上海: 同济大学, 2008.
[6] HAO H, ANG T C, SHEN J. Building vibration to traffic-induced ground motion[J]. Building and Environment, 2001, 36(7): 321-336.
[7] 马蒙, 刘维宁, 丁德云. 地铁列车引起的振动对西安钟楼的影响[J]. 北京交通大学学报, 2010, 34(4): 88-92.
MA Meng, LIU Weining, DING Deyun. Influence of metro train-induced vibration on Xi’an bell tower[J]. Journal of Beijing Jiaotong University, 2010, 34(4): 88-92.
[8] Mechanical vibration and shock evaluation of human exposure to whole-body vibration—Part 1:General requirements:ISO2631-1—1997[S]. 1997.
[9] CHOPRA A K. 结构动力学理论及其在地震工程中的应用[M]. 北京: 高等教育出版社, 2007.
[10] 廖振鹏. 工程波动理论导论[M]. 北京: 科学出版社, 2002.
[11] 钟才敏. 既有地铁运行区域新建建筑振动特点与设计方法研究[D]. 上海: 同济大学, 2016.
[12] 楼梦麟, 李守继. 地铁引起建筑物振动评价研究[J]. 振动与冲击, 2007, 26(8): 68-71.
LOU Menglin, LI Shouji. Evaluation of buildings’ vibration induced by underground trains [J]. Journal of Vibration and Shock, 2007, 26(8): 68-71.
[13] 苏亮, 邵寿磊. 多点地震输入的反应谱法研究[J]. 工程力学, 2014, 31(12): 83-88.
SU Liang, SHAO Shoulei. Research on response spectrum method for multi-support seismic excitations[J]. Engineering Mechanics, 2014, 31(12): 83-88.
[14] 楼梦麟, 李守继, 丁洁民, 等. 基于多点输入的地铁引起房屋振动评价研究[J]. 振动与冲击, 2007, 26(12): 84-87.
LOU Menglin, LI Shouji, DING Jiemin, et al. Quantitative evaluation of underground train-induced vibrations of a frame structure under multi-supports excitation[J]. Journal of Vibration and Shock, 2007, 26(12): 84-87.
Wholeprocessfieldtestsandanumericalsimulationofnewbuildingsinmetrooperationarea
ZHONGCaimin1, 2,MARenle1,WUXueshu2
(1.DepartmentofBuildingEngineer,TongjiUniversity,Shanghai200092,China; 2.ChinaArchitectureDesignGroupShanghaiJohnsonArchitectural&EngineeringDesigningConsultantsCo.,Ltd.,Shanghai200120,China)
Based on a new building adjacent to metro line, whole process field tests were performed on free field before construction and floors of different construction phases. The finite models of the building were established and numerical calculations were carried out by adopting different excitation modes. The calculated results were compared with the field test results. In the process of analysis, the numerical analysis method of “in situ excitation” was put forward in view of the environmental vibration. The results show that the “uniform excitation” input is only suitable for the preliminary prediction of small size building; the results of “in-situ excitation” and “multi-support excitation” input are accurate and reliable which can be used to predict the demand of different design phases. Meanwhile, “in situ excitation” or “multi-support excitation” could be chosen according to different requirements. When the field test results of free field are used as excitation to predict vibration, the calculation results can be amended according to different building types.
metro vibration; numerical simulation; in situ excitation; multi-support excitation;vibration prediction
2016-10-08 修改稿收到日期: 2016-12-29
钟才敏 男,博士生,高级工程师,1975年生
马人乐 男,教授,博士生导师,1951年生
TU921; TB533.2
A
10.13465/j.cnki.jvs.2017.20.027

