中国棉花期货与现货价格关系的实证研究

周畅，鞠荣华，杨智玲，杨汭华

（中国农业大学经济管理学院，北京100083）

中国棉花期货与现货价格关系的实证研究

周畅，鞠荣华*，杨智玲，杨汭华

（中国农业大学经济管理学院，北京100083）

通过协整检验、误差修正模型、Granger因果关系检验、脉冲响应函数以及方差分解等方法，对棉花期货价格与现货价格之间的关系进行了实证研究。结果发现我国棉花期货市场有较强的价格发现和套期保值功能，棉花期货价格对现货价格的影响程度较大，但现货价格对期货价格的影响程度较小。现有结论表明棉花相关企业可以利用期货市场规避价格风险，同时保险公司可以考虑推出棉花价格保险。

棉花；现货价格；期货价格；Granger因果关系检验；脉冲响应函数

国外对农产品期货市场价格发现功能的研究较多，研究方法也较为成熟。Robert[3]证明了期货市场具有价格发现和套期保值的功能。Wakita[4]利用大阪堂岛谷物期货市场上1760―1864年的月度数据和对应的现货数据进行了协整检验，表明两者之间存在长期均衡关系。Andrew等[5]运用协整检验和误差修正模型（Error correction model，ECM）分析了玉米、大豆、牛以及猪的期货价格和现货价格，发现从长远来看，这4个市场都是无偏的，但是在短期内玉米、牛以及猪的期货市场表现出低效率以及价格偏差。Maruiwa等[6]以美国棉花期货市场为例，利用1976年6月15日至1982年4月30日的日收盘价研究了棉花期货价格和现货价格之间的动态关系，研究表明棉花期货市场居于主导地位，具有价格发现功能。Kumar等[7]利用格兰杰（Granger）因果检验、协整检验以及ECM等模型研究了印度部分农产品期货市场的价格发现功能。中国关于期货价格与现货价格关系的实证研究起步较晚，大多直接使用国外较为成熟的理论和方法，但是，现有的对棉花期货价格发现功能的研究不仅没有得出一致的结论，而且还存在一定的不足。首先，朱桂宾[8]与王俊等[9]的研究均发现棉花的期货价格和现货价格之间只存在单向引导的关系，即期货价格对现货价格具有很强的引导作用，而现货价格对期货价格并没有引导作用，但刘磊等[10]、陈雪飞等[11]则认为棉花的期货价格和现货价格之间存在双向引导关系；其次，王俊等[9]的研究发现棉花期货的价格发现功能在短期内并不明显，而师树兴等[12]却发现棉花期货对现货价格已经形成了较明显的短期预测作用；再次，李慧茹[13]、李天忠等[14]、曾屹然[15]对棉花价格发现功能的研究选取了临近交割日的期货合约收盘价来代表期货价格，而临近交割期的期货合约交易量较小，并不能真实地反映当日期货市场的供求状况；最后，2013年9月16日我国正式实施新修订的《棉花细绒棉》标准（GB 1103―2012），中国棉花价格指数相应调整，棉花期货合约的基准交割品有所改变，故样本区间若跨越2013年9月则需检验数据是否发生结构性变化，以上研究都没有涉及棉花期货和现货价格的断点检验问题。本研究拟选取主力合约的收盘价，对棉花的期货、现货价格关系进行研究，在弥补现有研究不足的基础上，对棉花期货的价格发现功能做进一步研究，进而对已有研究结论进行检验。

2 数据处理与研究方法

2.1 数据来源与处理

2.1.1数据来源。期货品种选取郑州商品交易所一号棉花期货合约，棉花期货价格来自于郑州商品交易所官方网站公布的每日行情。选取主力合约（即成交量最大的合约）的每日收盘价作为当日的期货价格。棉花现货价格选取中国棉花价格指数，该指数是国内最早代表棉花现货价格水平的综合指标，也是棉花现货价格的权威指标。棉花现货价格主要来自中国棉花协会官网 （www.china-cotton.org）上发布的每日数据。由于2013年9月16日发布了新标准下的中国棉花价格指数，郑州商品交易所的一号棉花期货合约的基准交割品也由328级锯齿加工细绒棉改为3128B级锯齿加工细绒棉，本研究在选取现货价格时，2005年1月至2013年9月的现货价格选用的是CC Index 328的价格指数，2013年10月至2016年12月的现货价格选用的是CC Index 3128B的价格指数。同样，根据棉花价格指数的变化，棉花期货交割品级也从CF311合约开始由CC Index 328级细绒棉改为CC Index 3128B级细绒棉，该合约从2013年6月开始成为主力合约，因此选取2013年6月为期货价格序列的分界点。

2.1.2数据处理方法。棉花期货与现货价格均根据去除节假日后的每日数据求得月度平均数。本研究首先采用虚拟变量法[16]和邹（Chow）检验法[17]进行断点检验，判断2013年9月前后的棉花现货价格和2013年6月前后的棉花期货价格数据有无结构性变化，若没有结构性变化，则可使用棉花期货上市以来至2017年8月的价格连续数据，若有结构性变化，则只能使用2013年10月至2017年8月的价格连续数据。其次，由于棉花期、现货价格有较大幅度的波动且受季节变化的影响，因此对原始时间序列取对数并使用X-11-ARIMA方法进行了季节调整处理[18]，得到期货价格、现货价格2组时间序列数据LNFPSA和LNSPSA。

2.2 研究方法及步骤

首先，设置虚拟变量0和1，对样本期间棉花期、现货价格数据进行断点检验；其次，用扩展的迪克―富勒（Augmented Dickey-Fuller，ADF）检验[19]分析棉花期货价格、现货价格序列是否平稳，并判断两者之间是否存在长期协整关系；再次，用误差修正模型[20]判断期货价格和现货价格在短期偏离均衡状态时是否存在修正机制，并用格兰杰因果关系[21]来检验棉花期货价格对现货价格以及现货价格对期货价格的影响；最后，用脉冲响应函数以及方差分解来判断棉花期货价格与现货价格的影响方式及贡献度[22]。本研究实证分析所使用的软件是Eviews 8.0。

3 实证分析

3.1 棉花现货价格、期货价格断点检验

先采用虚拟变量法对棉花期货和现货价格这2组时间序列分别进行检验。对于棉花现货价格，设2005年1月至2013年9月的虚拟变量X1=0，2013年10月至2017年8月的虚拟变量X1=1；对于棉花期货价格，设2005年1月至2013年5月的虚拟变量X2=0，2013年6月至2017年8月的虚拟变 量X2=1，建立如下方程 ：SP=α1+β1X1+μt，FP=α2+β2X2+μt.其中SP代表棉花现货价格，FP代表棉花期货价格，X1和X2代表虚拟变量。对上述2个方程进行普通最小二乘 （Ordinary least square，OLS）回归，分别得如表1和表2所示的结果。

表1 棉花现货价格与虚拟变量的OLS回归结果

表2 棉花期货价格与虚拟变量的OLS回归结果

在棉花现货价格与虚拟变量的OLS回归结果中，虚拟变量回归系数的t统计量为－1.61，未通过10%显著性水平上的检验，由此看出，虚拟变量不能解释因变量SP，即棉花现货价格序列在2013年10月这个分界点没有发生结构性变化。在棉花期货价格与虚拟变量的OLS回归结果中，虚拟变量的回归系数在1%的水平上显著，可以解释因变量FP的变动，即期货价格数据存在断点，因此使用2005年1月至2017年8月的连续数据会影响实证分析结果的可信度。

再用Chow检验法对棉花期货价格和现货价格这2组时间序列进行断点检验，结果见表3。Chow检验的F值和P值显示，棉花现货价格与期货价格分别在2013年10月和2013年6月发生了结构性变化，因此不宜使用2005年至2017年的连续数据进行后续分析。因为最近的数据能更好地预测以后的情况，因此，在以下的实证分析中将使用2013年10月至2017年8月棉花期货和现货价格的月度数据作为样本。

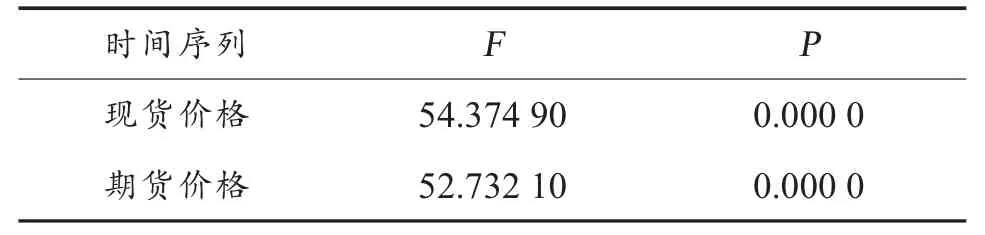
表3 棉花现货价格与期货价格Chow检验结果

3.2 相关性分析

从图1可以看出，2013年10月8日至2015年12月31日我国棉花期货与现货价格的变动趋势基本一致。

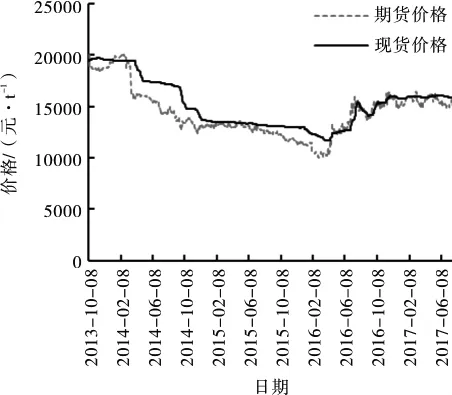
图1 我国棉花期货价格与现货价格走势

进一步计算我国棉花期、现货价格的相关系数为0.927 4。从统计分析标准来看，我国棉花期、现货价格的相关系数大于强相关指标（r=0.8），在一定程度上说明棉花期货价格对于棉花现货价格具有一定的发现作用。

3.3 ADF单位根检验

只有同阶单整的序列才能进行协整检验，需要分别对这2组数据序列进行ADF单位根检验，以判断这2组序列是否平稳。根据表4的结果，棉花期货价格、现货价格数据都是非平稳时间序列，但2个序列的一阶差分是平稳的，即序列LNFPSA和LNSPSA均为一阶单整序列。

表4 棉花期货和现货价格的ADF检验

3.4 协整检验

在时间序列LNFPSA和LNSPSA一阶单整的条件下，可以进一步判断它们之间是否存在协整关系。首先对LNFPSA和LNSPSA建立协整回归模型：LNSPSA=α+βLNFPSA+μt。 使用该模型进行OLS回归，得回归方程：LNSPSA=0.924 088+0.908 721LNFPSA.其中，LNFPSA回归系数的t统计量为17.80，在1%水平上显著；调整后的R2为0.872 773，拟合优度较好。该回归方程残差序列的ADF统计量为－2.402 467，小于5%显著性水平的临界值（－1.948 495），可以认为残差序列不存在单位根，为平稳序列。因此，序列LNFPSA和LNSPSA具有长期协整关系，可以建立误差修正模型。由上面的回归方程式可以定义现货价格误差修正项（ECM1）为：ECM1t－1=LNSPSAt－1－0.242 185LNFPSAt－1.同理，定义期货价格的误差修正项（ECM2）为：ECM2t－1=LNFPSAt－1－0.989 579LNSPSAt－1.

误差修正模型的估计结果见表5。棉花现货价格的ECM项系数是负值，在1%的水平上显著，说明现货市场价格具有反向修正机制，当棉花现货市场价格偏离均衡状态时，误差修正项会使其向均衡状态收敛。棉花期货价格的ECM项系数也是负值，在10%的水平上显著，说明期货价格也存在反向修正机制，当棉花期货价格偏离均衡状态时，误差修正项也会使其向均衡状态收敛。但因2个误差修正项系数绝对值较小，所以其均衡调整的力度并不大。

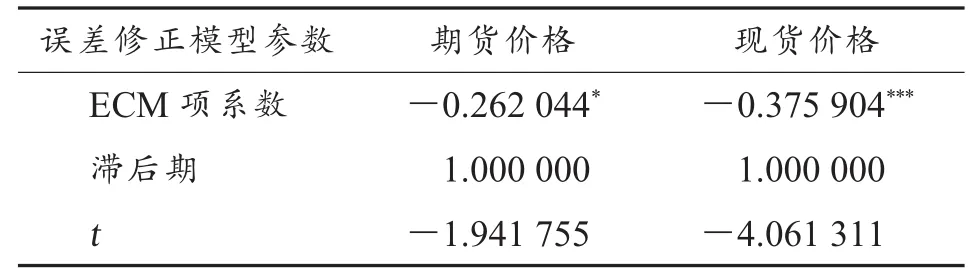
表5 误差修正模型检验结果

3.5 Granger因果关系检验

格兰杰因果关系检验对于变量是否平稳非常敏感，由于序列LNFPSA和LNSPSA都是非平稳序列，而一阶差分序列是平稳序列，所以使用一阶差分序列DLNFPSA和DLNSPSA来进行格兰杰因果关系检验[7]，检验结果见表6。可以看出，棉花现货价格与期货价格存在相互引导的关系。

表6 Granger因果关系检验结果

3.6 脉冲响应函数

得出棉花期货与现货价格相互引导的结论之后，用脉冲响应函数来分析棉花期货价格和现货价格这2个变量对其自身以及另一变量的扰动的响应，检验结果见图2（纵轴为单位冲击引起的波动，横轴为波动持续的期数）。

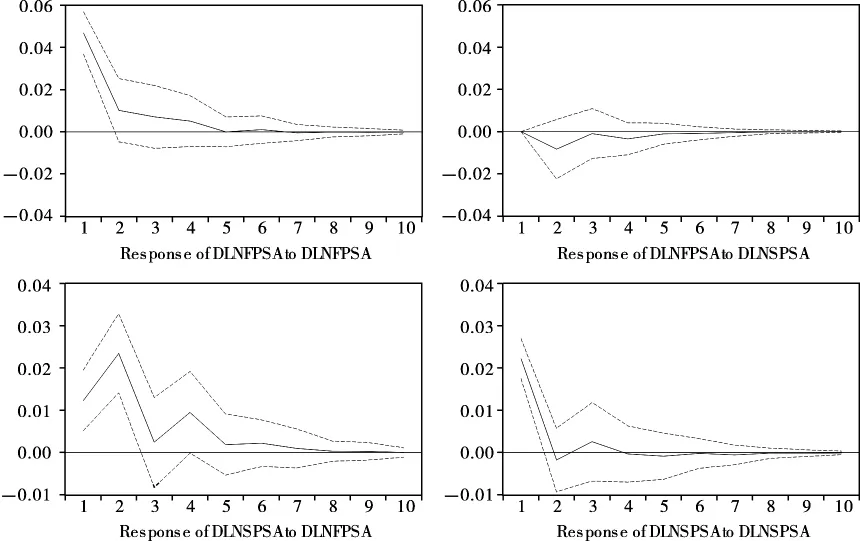
图2 棉花期货价格与现货价格脉冲响应函数分析

棉花期货价格对其自身1个标准差新息的冲击立即做出了响应，大约在0.05，之后逐步下降，并从第5期开始趋向于零。棉花现货价格对其自身的扰动也立即做出了响应，大约为0.02，之后逐步下降，第2期仅有0.002且为负向，第3期增加至0.003且为正向，之后逐步下降并于第4期开始趋向于零。棉花期货价格对现货价格的扰动并没有立即做出响应，第2期响应约为0.01且为负向，第3期逐步缩小为零，第4期稍有负向的波动，但于第5期开始趋向于零。棉花现货价格对期货价格的扰动立即做出了响应，第1期为0.01，第2期达到最大且为正向，第3期逐步下降，第4期又稍有上升，之后逐步下降并于第8期开始趋向于零。这表明棉花期货价格的变动会引起棉花现货价格的同向变动，而棉花现货价格的变动会引起期货价格反向变动，但是整体来看，棉花现货价格对期货价格的影响较小。

3.7 方差分解

利用方差分解方法对棉花期货价格对现货价格变化的贡献度以及现货价格对期货价格变化的贡献度进行分析，结果见表7。

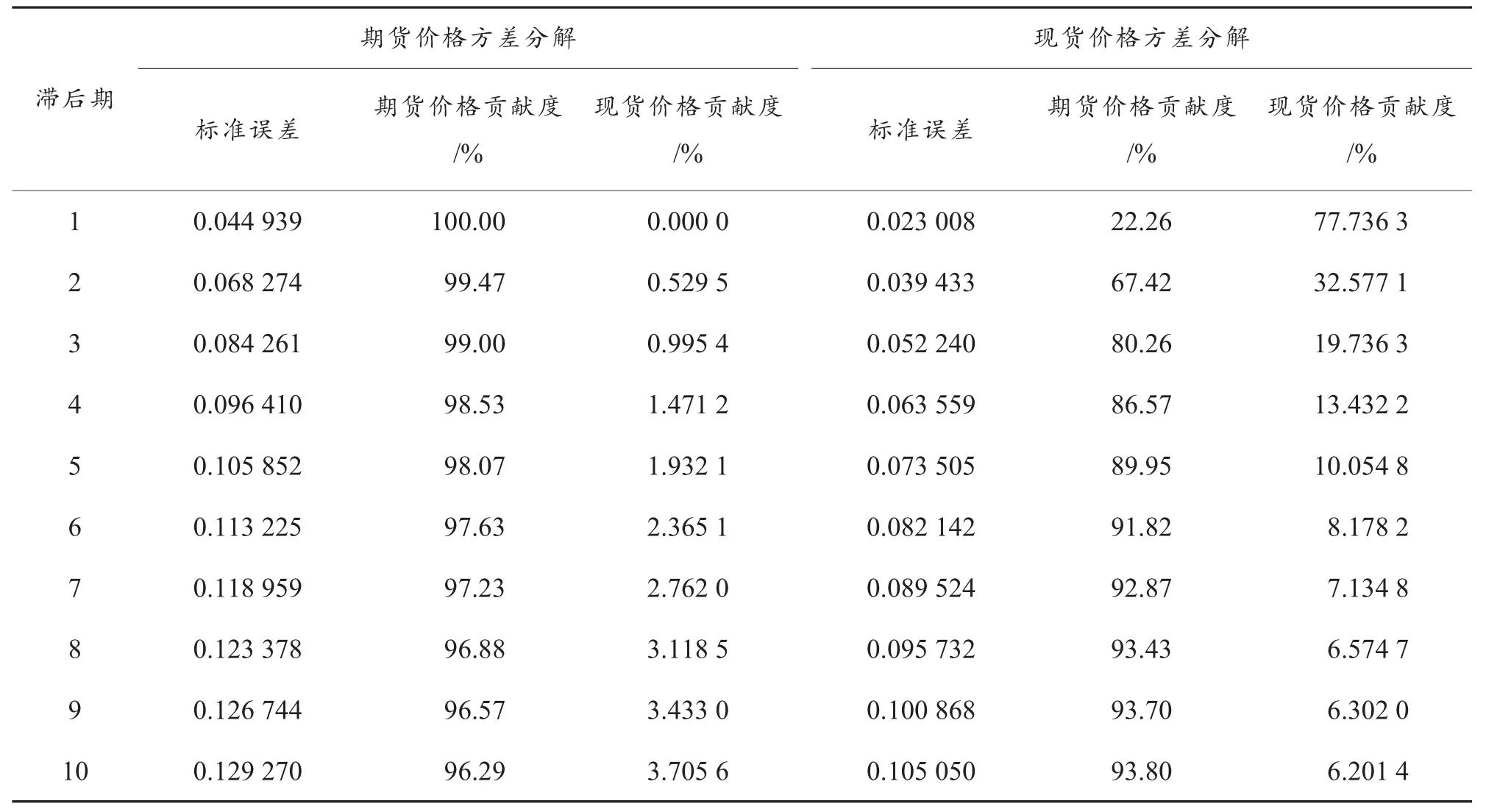
表7 棉花期货价格、现货价格方差分解结果

由表7可以看出，在第1期预测中，棉花期货价格自身占预测方差的100%，之后逐渐减小并于第8期开始稳定在96%左右，说明棉花期货价格预测方差约有96%是由期货价格自身的扰动所引起的，仅有约4%是由现货价格扰动引起的。棉花现货价格自身贡献度在第1期预测中占预测方差的77.7%，随着滞后期增加而逐渐减小，大约于第8期开始趋于稳定，棉花现货价格预测方差约有93%是由期货价格扰动引起的，约7%是由其自身的扰动引起的。由此推断，棉花期货价格变化对现货价格的影响非常大，而现货价格变化对期货价格的影响相对较小。

4 结论与建议

选取2013年10月至2017年8月棉花期货和现货的月度价格，对我国棉花期、现货价格之间的关系进行实证研究发现：（1）棉花期货、现货价格存在协整关系，并且棉花期货价格与现货价格相互引导，为棉花现货的套期保值提供了前提条件。（2）期货价格对现货价格有较大的影响，说明棉花期货市场有较强的定价功能；同时现货价格也能够在一定程度上影响期货价格的变动，说明期货市场定价有一定的现货基础。（3）期货与现货价格在短期偏离均衡状态时最终均可以调整至长期均衡状态。以上研究结论表明，我国棉花期货市场能够较好地发挥价格发现和套期保值两大功能。基于此，棉花相关企业可以利用棉花期货市场进行套期保值，规避价格风险；同时保险公司也可以通过在棉花期货市场上锁定棉花的未来价格，推出棉花价格保险或收入保险；棉农可以通过购买保险公司的棉花价格保险或收入保险而规避棉花生产的价格风险。但是，方差分解分析也发现，棉花期货价格对现货价格的影响程度较大，而现货价格对期货价格的影响程度较小，表明我国棉花的期货市场和现货市场有待进一步完善。

[1]蔡胜勋.新形势下我国农产品期货市场发展路径研究[J].金融理论与实践，2016(5)：87-90.

[2]庞贞燕，刘磊.期货市场能够稳定农产品价格波动吗——基于离散小波变换和GARCH模型的实证研究[J].金融研究，2013(11)：126-139.

[3]Robert W K.Futures,options and swaps[M].New York:Oxford,1999.

[4]Wakita S.Efficiency of the Dojima rice futures market in Tokugawa-period Japan[J].Journal of Banking&Finance,2001,25(3):535-554.

[5]Andrew M,Matthew T.Market efficiency in agricultural futures markets[J].Applied Economics,2002,34(12):1519-1532.

[6]Maruiwa H,Tokutomi T,Hirohata M,et al.Investigation of price discovery and efficiency for cash and futures cotton prices[J].Western Journal of Agricultural Economics,2009,9(1):172-177.

[7]Kumar B,Pandey A.Market efficiency in Indian commodity futures markets[J].Journal of Indian Business Research,2013,5(2):101-121.

[8]朱桂宾.基于G-S模型我国棉花期货市场和现货市场在价格发现功能中作用的实证分析[J].中国证券期货，2009(10)：32-33.

[9]王俊，梁朝晖.我国棉花期货价格发现功能的实证研究[J].金融经济，2014(20)：59-62.

[10]刘磊，张明辉.中国棉花期货价格发现功能：基于中美棉花期货的比较研究[J].金融理论与实践，2010(8)：21-24.

[11]陈雪飞，谢高强，沈淑娟.我国棉花期货价格发现功能研究[J].统计与决策，2013(20)：165-167.

[12]师树兴，唐惠明.我国棉花期货价格发现功能的实证分析[J].金融经济，2011(24)：89-91.

[13]李慧茹.中国棉花期货市场价格发现功能研究[J].运筹与管理，2006(6)：95-99.

[14]李天忠，丁涛.我国农产品期货价格对现货价格先行性的实证研究[J].金融理论与实践，2006(10)：16-19.

[15]曾屹然.我国棉花期货市场与现货市场关系研究[D].北京：首都经济贸易大学，2015.

[16]杨帆，韩传峰.中国交通基础设施与经济增长的关系实证[J].中国人口：资源与环境，2011，21(10)：147-152.

[17]易丹辉.数据分析与Eviews应用[M].北京：中国人民大学出版社，2014.

[18]王书平，李建平，高丽君，等.基于X-11-ARIMA方法的取暖油价格季节性波动分析[J].数理统计与管理，2007，26(1)：62-67.

[19]Bhargava A.On the theory of testing for unit roots in observed time series[J].The Review of Economic Studies,1986,53(3):369-384.

[20]Ghosh A.Cointegration and error correction models:Intertemporal causality between index and futures prices[J].Journal of Futures Markets,1993,13(2):193-198.

[21]Granger C W J.Testing for causality:A personal viewpoint[J].Journal of Economic Dynamics and Control,1980(2):329-352.

[22]张宗成，王骏.基于VAR模型的硬麦期货价格发现研究[J].华中科技大学学报(自然科学版)，2005(7)：103-106.

Empirical Study on the Relation between Cotton Spot and Futures Price in China

Zhou Chang,Ju Ronghua*,Yang Zhiling,Yang Ruihua

F326.12：S562

A

1000-632X（2017）10-0006-07

10.11963/1000-632X.zcjrh.20171012

1 引言

棉花价格的剧烈波动会对棉花生产者和经营者产生不利影响，甚至造成整个国民经济的损失：对于棉农而言，价格波动使其无法合理安排种植面积，棉花产量会大起大落；对于棉花企业而言，价格波动会使其无法估算成本和收益，进而承担较高的价格风险。棉花期货市场的价格发现和套期保值功能对棉花产业的健康发展具有至关重要的作用。如果棉花期货具有良好的价格发现功能，那么棉花企业就可以通过期货市场进行套期保值，从而规避价格风险；而保险公司就会具备推出棉花价格保险的条件，被期货市场拒之门外的棉农可以通过价格保险来稳定收入。此外，有学者也指出完善的期货市场可以调节农作物生产结构[1]，稳定农产品价格[2]。因此，对棉花期货市场价格发现功能的研究具有重要的意义。

2017-07-07

*通信作者：juronghua@cau.edu.cn

农业部软科学课题（201608-2）