不等式恒成立问题解法直通车

高金花

新课标下的高考越来越注重对考生的综合素质的考查，恒成立问题便是一个考查考生综合素质的很好途径，它常以函数、方程、不等式和数列等知识点为载体，渗透着换元、化归、分类讨论、数形结合、函数与方程等思想方法，在培养思维的灵活性、创造性等方面起到了积极的作用.近几年的数学高考中频频出现恒成立问题，其形式逐渐多样化，但都与函数、导数知识密不可分.解决高考数学中的恒成立问题常用以下几种方法：①函数性质法；②主参换位法；③分离参数法；④数形结合法；⑤消元转化法.下文举例说明.

一、函数性质法

二次不等式恒成立问题，往往采用这个方法.它主要有以下几种基本类型：

二、分离参数法

若所給的不等式能通过恒等变形使参数与主元分离于不等式两端，从而问题转化为求主元函数的最值，进而求出参数范围.利用分离参数法来确定不等式f（x，λ）≥0（x∈D，λ为实参数）恒成立中参数λ的取值范围的基本步骤：

（1）将参数与变量分离，即化为g（λ）≥f（x）（或g（λ）≤f（x））恒成立的形式；

（2）求f（x）在x∈D上的最大（或最小）值；

（3）解不等式g（λ）≥f（x）max（或g（λ）≤f（x）min），得λ的取值范围.

适用题型：（1）参数与变量能分离；（2）函数的最值易求出.

三、反客为主法

某些含参不等式恒成立问题，在分离参数会遇到讨论的麻烦或者即使能容易分离出参数与变量，但函数的最值却难以求出时，可考虑变换思维角度“反客为主”，即把习惯上的主元变量与参数变量的“地位”交换一下，换个视角重新审查恒成立问题，往往可避免不必要的分类讨论或使问题降次、简化，起到“山穷水尽疑无路，柳暗花明又一村”的效果.

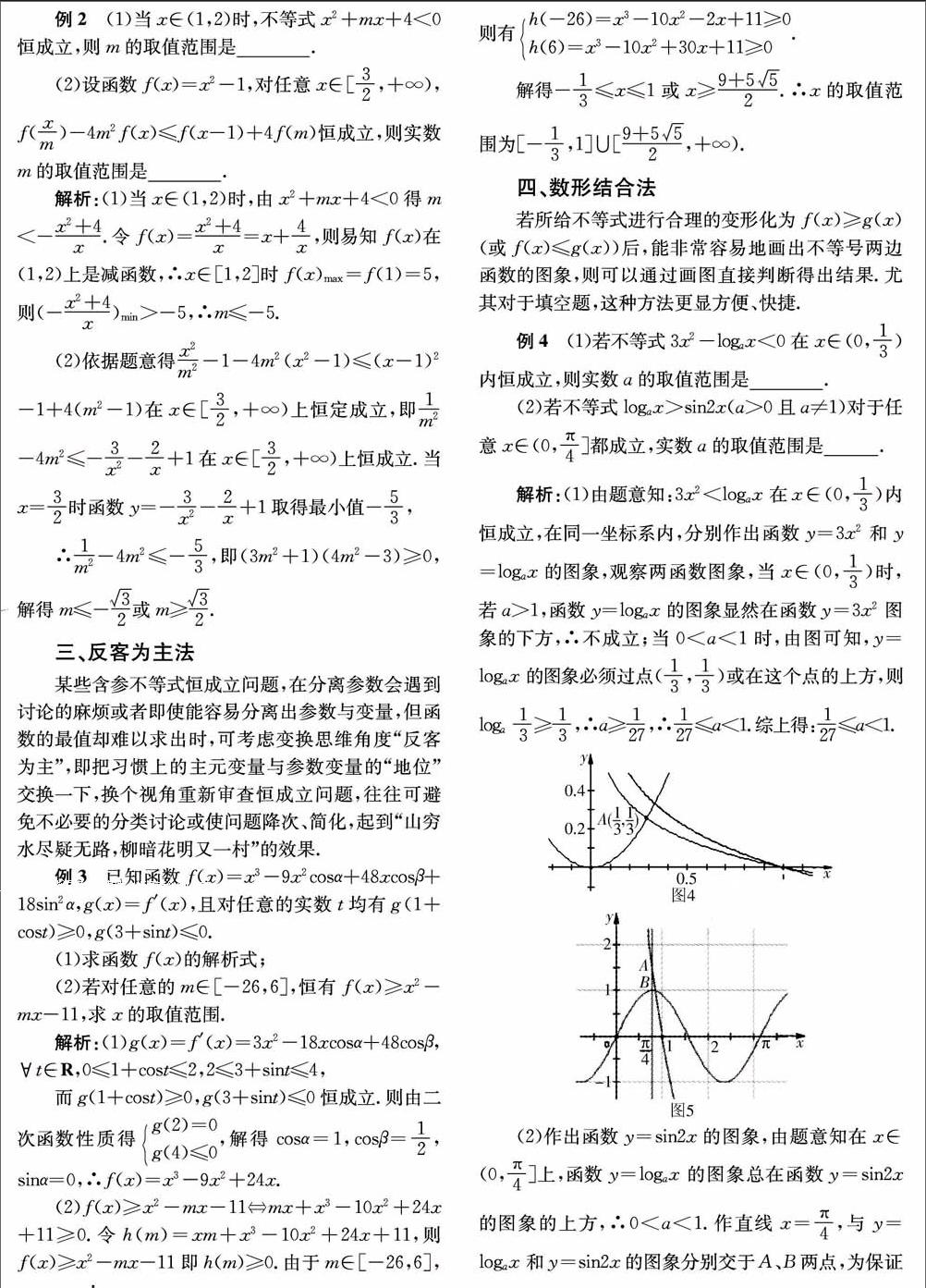
四、数形结合法

若所给不等式进行合理的变形化为f（x）≥g（x）（或f（x）≤g（x））后，能非常容易地画出不等号两边函数的图象，则可以通过画图直接判断得出结果.尤其对于填空题，这种方法更显方便、快捷.

五、消元转化法

对于含有两个以上变量的不等式恒成立问题，可以根据题意依次进行消元转化，从而转化为只含有两变量的不等式问题，使问题得到解决.

上述例子剖析了高考数学中恒成立问题的题型及解法，值得一提的是，各种类型各种方法并不是完全孤立的，虽然方法表现得不同，但其实质却都与求函数的最值是等价的，这也正体现了数学中的“统一美”.endprint