一种手持式MEMS磁力计的罗差校正方法*

李思民,蔡成林,王亚娜,曹振强

(桂林电子科技大学 信息与通信学院,广西桂林541004)

一种手持式MEMS磁力计的罗差校正方法*

李思民,蔡成林*,王亚娜,曹振强

(桂林电子科技大学 信息与通信学院,广西桂林541004)

针对手持式MEMS磁力计使用过程中航向精度低的问题,在分析磁力计误差的基础上,建立了罗差校正模型,推导了罗差系数的计算公式,采用椭圆假设、约束最小二乘法、解卷绕和滑动窗口滤波等方法降低磁力计航向误差。该校正过程简单方便,只需手持MEMS传感器组旋转一周。实验结果表明,该校正方法具有良好的抗噪声性能,校正后的磁力计航向精度优于1°。

MEMS传感器;罗差校正;椭圆拟合;磁力计;最小二乘法

随着微机电系统MEMS(Micro-Electro-Mechanical-System)传感器的应用日渐广泛,它在航天、导航、机器人等领域的重要性日益凸显[1]。其中,MEMS感器组最为常见,它主要包括三轴磁力计、三轴加速度计、三轴陀螺仪。

磁力计作为一种磁场测量仪器,通过测量周围磁场在三轴磁力计上的分量来计算航向角,具有体积小、功耗低、成本低,可靠性高、航向误差不随时间累积等优点[2]。但是,磁力计在使用过程中容易受到外界坏境的干扰,为了提高航向精度,在使用之前需要对磁力计进行校正。

目前磁力计误差补偿常用方法有泊松模型补偿法[3]、椭圆拟合补偿法[4-6]、椭球拟合补偿法[7-8]、基于外部航向基准辅助的罗差补偿法[9]等方法。泊松模型补偿法,可采用十二位置翻滚法或者借助外部姿态参考数据进行最小二乘递推等方法来确定12个参数,补偿过程操作复杂,计算量大[3]。文献[4-6]利用椭圆补偿法对磁力计进行校正,在无磁转台上进行实验,补偿效果较好,然而在实际使用中,用户通常是手持测量设备工作,所以研究手持式磁力计校正方法具有实际应用价值。椭球拟合补偿法是将二维拟合扩展至三维,其补偿精度比椭圆拟合效果好,但校正过程相对椭圆补偿较为复杂[7-8]。基于外部航向基准补偿方法,在校正过程中需要外部航向作为基准,补偿效果佳,但在实际应用中往往没有航向基准作为参考,故该方法的实用性较差[9]。

1 磁力计原理

地球磁场是弱磁场,强度大概为0.5 Gauss～0.6 Gauss。地磁强度水平分量的矢量和始终指向磁北,磁力计算出的航向角为前进方向和磁北的夹角α。在实际应用中所参考的北指的是地理北,磁北和地理北并不重合,它们之间的夹角称为磁偏角β。因此,在实际使用中,真实航向角ψ=α+β,当地磁偏角可以通过查表获得。地磁场示意图如图1所示,β为磁偏角,T为地磁强度,I为磁倾角。

图1 地磁场示意图

磁力计在水平放置且不受任何磁干扰的情况下,通过测量磁力计X、Y轴方向的地磁强度Hx、Hy,便可通过式(1)确定载体相对于磁北的航向角:

(1)

2 磁力计罗差分析

MEMS磁力计的误差是可以分为两类:第1类是由系统本身所产生的误差,包括制造误差、安装误差、罗差等,这类误差可以归结于对磁力计三轴原始输出的影响;第2类是由姿态引起的误差,这类误差是由平台倾斜产生。

(2)

在实际应用中,罗差是导致航向精度下降的主要原因,它分为硬磁干扰和软磁干扰。硬磁干扰主要是由于周围坏境中的永久磁铁物质引起,它们产生的磁场强度认为是恒定不变的,即硬磁材料所合成的磁场投影到磁力计3个轴上的分量是恒定的。软磁干扰主要是周围坏境中的铁磁物质引起,软磁材料本身不具有磁性,受到周围磁场影响后产生磁场,其影响程度和方向与磁力计的位置有关,干扰程度与方向有关。

在磁力计处于水平且无任何误差的情况下,将磁力计旋转一周并采集X、Y轴的数据,它们在坐标平面下的映射为圆心在原点上的正圆。受到硬磁干扰时,会使正圆偏离原点,干扰越大偏离越远。受到软磁干扰时,正圆会畸变成椭圆,干扰越大畸变越严重。磁力计校正过程就是把椭圆变成圆心在原点的正圆。

3 最佳椭圆假设

在平面坐标系中,可以采用圆锥曲线方程来表示任意位置的椭圆:

(3)

采用直接最小二乘法拟合得到的圆锥曲线不一定是椭圆,所以需要根据椭圆曲线的性质,在拟合椭圆的同时加上约束条件以保证拟合出的曲线为椭圆,选取4AB-C2=1作为椭圆拟合的约束条件,椭圆系数求解转化为约束条件下求极值问题[12]:

(4)

式中:

根据拉格朗日乘数法,引入参数λ,将式(4)转化为求解约束条件下的极值问题:

(5)

经过上述推导,可以得出约束条件下最小二乘法椭圆拟合最终是需要求出矩阵(DTD,C)的6个广义特征值和对应的特征向量,特征值中只有一个大于0,所求椭圆系数矩阵K为特征值大于0对应的特征向量。

罗差校正过程就是把偏离圆心的椭圆校正为正圆。从圆到椭圆的过程可以描述为:

(6)

由式(6)可以得出XY轴补偿后的磁场值为:

(7)

式中:椭圆系数矩阵K=(A,B,C,D,E,F)T与式(6)的关系为:

(8)

(9)

(10)

对于矩阵L,由于求解航向时只与Lx/Ly有关,而与它们的值无关,为了方便求解,假设Lx为1,则有

Ly=A/B

(11)

综上所述,磁力计罗差处理过程为:首先将采集到三轴地磁数据通过式(2)进行倾斜补偿,然后用约束条件下的最小二乘法对数据进行椭圆拟合,并求出的椭圆系数,再根据式(7)求出补偿后的XY轴磁场值。

4 系统设计与实验结果分析

罗差校正实验在室内进行验证,校正过程中手持MEMS传感器组进行实验。MEMS传感器组将加速度计、陀螺仪、磁力计对应轴同向组合成惯性传感器的3个轴向。

磁力计在实验过程中由于手部的抖动,会导致系统振动,所以磁力计在数据采集期间除了会受到硬磁材料和软磁材料干扰之外,还会因为手部的抖动产生噪声。手部抖动产生的噪声可以通过滑动窗口滤波得到改善,公式如下:

(12)

式中:2N+1为滑动窗口的长度,由磁力计的采样频率决定。

由于航向角在0～360°之间存在卷绕现象,在窗口平滑滤波之前还需对求解出的航向角解卷绕,即将航向角取值范围从0～360°变换至-N1×360或+N2×360范围内,其中顺时针旋转为正,逆时针旋转为负,N1、N2由旋转次数决定。

4.1 硬件电路框架

本文提出的罗差校正方法是基于MEMS传感器组。它包括三轴磁力计(HMC5883L)、三轴加速度计和三轴陀螺仪(MPU6050)、微控制器(STM32F103)。硬件电路框图如图2所示,首先将加速度计、陀螺仪和磁力计的原始数据通过A/D转换,然后对数据进行预处理,并通过微控制器对数据进行融合,解算出平台的姿态角[13]。

图2 硬件电路框图

4.2 软件部分设计

在实验过程中,首先获取加速度计、陀螺仪、磁力计的数据,用keil软件进行C语言编程,通过四元数姿态解算和卡尔曼滤波得出准确的横滚角、俯仰角、航向角和三轴原始磁数据,并通过串口输出至上位机并保存成Excel文件格式。

为了对校正前后的航向误差进行分析,罗差校正算法在MATLAB中实现,算法流程如图3所示,首先读取Excel表格中的数据,将横滚角、俯仰角作为倾斜偿的输入,航向角作为误差分析的参考航向。三轴磁力计数据在倾斜补偿之后进行椭圆补偿,再通过解卷绕、滑动窗口滤波剔除抖动噪声,最后输出校正后的航向角。

图3 罗差校正流程图

4.3 实验结果分析

实验以传感器组通过四元数姿态解算和卡尔曼滤波之后的航向角为基准分析磁力计的航向误差[14]。实验过程,首先手持MEMS传感器组旋转360°收集三轴地磁数据作为校正数据,然后再次旋转360°,每间隔90°停留一段时间,并收集三轴地磁作为实验数据。

校正数据经式(2)倾斜补偿之后,将XY轴的地磁数据进行最佳椭圆拟合,如图4所示。

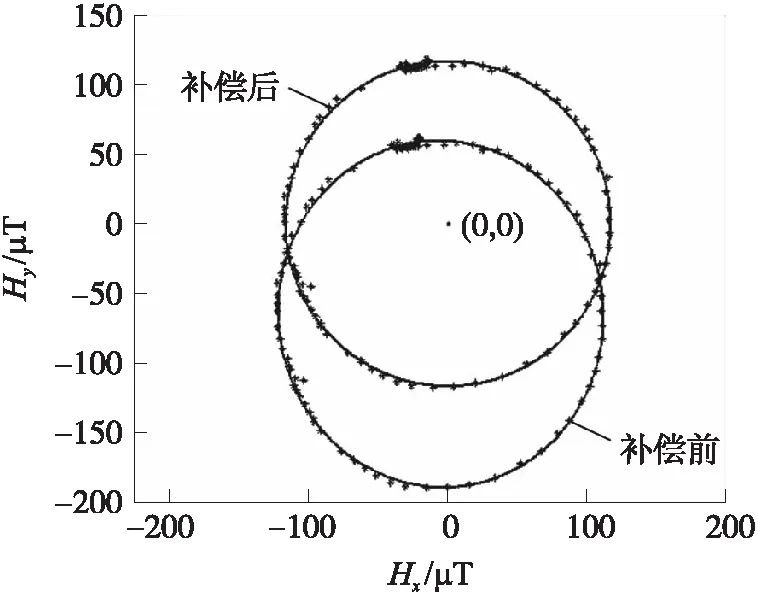
图4 椭圆补偿

从图4可以看出校正数据直接拟合出来的是偏离原点的椭圆,通过补偿之后椭圆变成圆心在原点的正圆。

图5对罗差校正前后的航向误差与滤波前后的航向误差进行了对比。从图中可以看出,使用未校正未滤波(虚线)的地磁数据求出的航向角,由于附近硬磁材料、软磁材料和手部抖动噪声的影响,其航向误差约为±31°;使用已校正未滤波(点虚线)的地磁数据求出的航向角,其航向误差相比前者有较大改善,但磁力计在旋转过程中,由于手部抖动噪声的存在,使航向精度在旋转过程产生较大的偏差,其航向误差约为±11°;使用已校正已滤波(粗实线)的地磁数据求出的航向角,由于抖动噪声被有效限制,其航向误差降低至±1°之内。

图5 航向误差

5 结束语

本文提出的手持式MEMS磁力计罗差校正方法,在周围存在软硬磁干扰的情况下,只需手持磁力计旋转一周即可对罗差进行校正。在使用过程中,由于平台倾斜和手部抖动引起的误差,通过倾斜补偿、解卷绕、滑动窗口滤波进行修正。实验结果表明,校正后的航向精度高,在对航向角有严格要求的室内导航中具有较高的应用价值。

[1] 李荣冰,刘建业,曾庆化,等. 基于MEMS技术的微型惯性导航系统的发展现状[J]. 中国惯性技术学报,2004,12(6):88-94.

[2] 陈洁,黄庆安,秦明.MEMS磁场传感器的研究进展[J]. 电子器件,2006,29(4):1384-1388.

[3] 郭鹏飞,任章,邱海韬,等. 一种十二位置不对北的磁罗盘标定方法[J]. 中国惯性技术学报,2007,15(5):598-601.

[4] 孙宏伟,房建成,李艳.椭圆拟合方法在磁罗盘罗差校准中的应用[J]. 光学精密工程,2009,17(12):3034-3039.

[5] 秦涛,马建仓,王彤,等. 电子罗盘最佳椭圆误差补偿方法[J]. 传感技术学报,2013,26(11):1499-1503.

[6] 秦勇,赵杰,王晓宇.基于椭圆拟合误差补偿算法的数字磁罗盘[J]. 吉林大学学报(工学版),2009,39(2):489-493.

[7] 李智,李翔.基于椭球假设的三轴电子罗盘罗差补偿研究[J]. 仪器仪表学报,2011,32(10):2210-2215.

[8] FANG J C,SUN H,CAO J J,et al. A Novel Calibration Method of Magnetic Compass Based on Ellipsoid Fitting[J]. IEEE Instrumentation and Measurement Society.2011,60(6):2053-2061.

[9] 曹平军,吕冰. 基于误差补偿的电子罗盘抗干扰设计[J]. 仪表技术与传感器,2013(3):22-24.

[10] 邵婷婷,马建仓,胡士峰,等. 电子罗盘的倾斜及罗差补偿算法研究[J]. 传感技术学报,2007,20(6):1335-1337.

[11] 闫蓓,王斌,李媛.基于最小二乘法的椭圆拟合改进算法[J]. 北京航空航天大学学报,2008,34(3):295-298.

[12] 邹益民,汪渤. 一种基于最小二乘的不完整椭圆拟合算法[J]. 仪器仪表学报,2006,27(7):808-812.

[13] 米刚,田增山,金悦,等. 基于MIMU和磁力计的姿态更新算法研究[J]. 传感技术学报,2015,28(1):43-48.

[14] 贾瑞才.基于四元数EKF的低成本MEMS姿态估计算法[J]. 传感技术学报,2014,27(1):90-95.

ErrorCalibrationMethodofMagneticDeviationforHand-HeldMEMSMagnetometer*

LISimin,CAIChenglin*,WANGYana,CAOZhenqiang

(Institute of Information and Communication,Guilin University of Electronic Technology,Guilin 541004,China)

Due to the limitation of heading accuracy in Hand-held MEMS magnetometer,a magnetometer error model was established to improve its accuracy,which is based on the analysis of magnetometer error,meanwhile,the formula of magnetic deviation coefficient was deduced. Some methods of dealing with the data,which included elliptic assumption,least square method,unwrapping and smoothing window filter,were adopted to reduce the heading error of magnetometer. The experiment shows that the operation is simple. Just holding a set of MEMS sensor and rotating it around the whole operation is completed. This method is of stronger anti-noise ability,whose corrected accuracy of heading angle is better than 1°.

Key words:MEMS sensor;magnetic deviation calibration;ellipse fitting method;magnetometer;least squares method

10.3969/j.issn.1005-9490.2017.05.027

项目来源:空天无源探测平台的差分定位体制研究项目(612630028)

2016-07-14修改日期2016-08-17

TP216.1

A

1005-9490(2017)05-1191-05

李思民(1991-),男,汉族,湖南祁东人,桂林电子科技大学信息与通信学院,硕士研究生。研究方向为室内外无缝导航,lisimin523@126.com;

蔡成林(1969-),男,汉族,湖南双峰人,教授,博士,硕士生导师,研究方向为卫星导航与无线通信、时空基准与位置服务、室内外无缝定位等,chengcailin@126.com。