无线传感器网络中基于无标度特性的拓扑控制算法*
刘洲洲,李文威
(西安航空学院传感器网络与智能计算实验室,西安 710077)
项目来源:国家自然科学基金项目(61601365);陕西省自然科学基础研究计划面上项目(2017JM6096);陕西省教育厅科研计划项目(16JK1395);西安市科技计划项目(2017076CG/RC039(XAHK001))
2017-02-15修改日期2017-07-05
无线传感器网络中基于无标度特性的拓扑控制算法*
刘洲洲*,李文威
(西安航空学院传感器网络与智能计算实验室,西安 710077)
针对无线传感器网络中的无标度特性中的抗毁和容错能力差问题进行了研究,提出了一种改进的无标度网络拓扑控制算法(BA Evolution Model,BAEM)。通过分析幂率指数对网络容错和拓扑抗毁性的影响,得出在兼顾拓扑容错性的同时最大化网络抗毁性的最优网络拓扑。仿真实验结果表明:改进后的容错拓扑可以保持无标度网络模型对随机故障较强的鲁棒性,同时可以改善无标度网络对蓄意攻击的脆弱性,并延长了网络生命周期。
无线传感器网络;无标度;抗毁;容错
无线传感器网络WSNs(Wireless Sensor Networks)节点经常部署在恶劣的环境中,拓扑构建主要考虑电池能源无法更新的情况[1],因此,所得WSNs拓扑必须具有很强的容错性,以应对频繁出现的节点失效现象[2]。此外,无人值守的WSNs可能因遭受目的性的攻击直接或间接的导致整个网络的瓦解。所以,如何提高整个网络的抗毁性即抗毁性也成为构建WSNs的重要课题。
近期对于无线传感器网络容错拓扑的研究,主要是通过功率控制生成能量最小的k-连通网络拓扑[3-5],基本思想是把容错拓扑问题等价为寻找多连通图,然而,寻找能量最优的多连通图问题被证明是NP难的。无标度特性(少数的节点往往拥有大量的连接,而大部分节点却拥有很少的连接)的发现作为复杂网络研究中的一大突破,其具有的强容错性可以解决WSNs中的容错问题。文献[5]设计了一种基于势博弈的拓扑控制模型,并证明了该模型纳什均衡的存在性。通过构造兼顾节点连通性和能耗均衡性的收益函数,以确保降低节点功耗的同时维持网络的连通性。而当经典BA模型BA(Barabsi-Albert Model)提出以后,文献[6]将随机网络和BA无标度网络中某些关键节点去除后两种网络的鲁棒性进行了对比,由于无标度网络的幂率特性,使其具有较强的容错性,但是在面对蓄意攻击时却比较脆弱。因此如何设计和优化一个网络,使其具有较强的容错能力和抗攻击能力显得尤为重要并且迫切,文献[7]重点分析了EAEM(Energy-Aware Evolution Model)算法[8-9]研究如何构建能量有效的无标度拓扑结构,它在择优连接时考虑节点的剩余能量,促使网络向节能的方向转变。Qi等人[10]将随机连接改进为基于节点适应度的优先连接,并将适应度的计算与节点能量直接关联。Wang[11-12]等人采用优化度分布熵的方法,优化网络的度分布指数,增加网络的异质性,达到提高网络容错能力的目的。Wu等人[13]对无标度拓扑结构非均匀性的研究发现标度指数越大,网络越均匀。受此启发,可以使用新的网络模型,使网络尽量均匀,并继承无标度网络的强容错性,最终实现提高网络的抗攻击性和延长生命期的目的。
基于上述分析,为了在兼顾拓扑容错能力的同时增强网络的抗攻击能力,需要构造满足不同网络需求的容错拓扑结构。本文提出了一种新的无标度网络演化模型BAEM(BA Evolution Model),通过分析幂率指数对网络抗毁性和拓扑容错性的影响,得出一种满足特定网络需求的强容错无标度拓扑。
1 问题模型
1.1 无标度网络抗毁和容错建模
由文献[10]的分析可知,当无标度的幂率指数λ>2时,网络的抗毁性随着幂率指数的增大而减小。传统BA无标度网络模型中节点的最大度随着网络规模无限增大,使得网络中存在少数度非常大的hub节点,这使得无标度网络在选择性攻击度大的节点时异常脆弱。对于无标度网络的最大节点度计算如下:
设无标度网络度分布为p(k)=Ck-λ,系数C可归一化估计如下
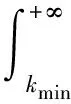
(1)

C=(λ-1)mλ-1
(2)
网络的最大节点度kmax可用下式进行估计:

(3)
结合式(2)和式(3)可得
kmax=mN1/(λ-1)
(4)
由式(4)可知,kmax与网络增长规模m、节点数N和幂率指数λ有关,通常情况下网络的增长规模m=1,在不同节点数N的情况下画出kmax与幂率指数λ的函数关系图如图1所示。

图1 最大节点度与幂率指数关系函数图
由图1可知,kmax随着幂率指数的增大而减小,这说明幂率指数越小,最大节点度越大,网络的抗毁性就越差。以提高无标度网络的抗攻击能力为目的,优化网络结构,可以用kmax来度量无标度网络整体的非均匀性。在网络节点数N和网络增长规模m给定的情况下,kmax越小,标度指数越大λ越大,网络越均匀,抗毁性就越好,但容错性较差,如随机网络;而kmax越大,标度指数λ越小,网络越不均匀,网络抗毁性越差,但容错性能较好,如星型网络。所以要构造强抗毁性的无标度拓扑就要minkmax。
其中Cohen等人[11]对无标度网络的相变性质进行了深入研究,他们得到了一个网络存在最大连通集团的判定标准:k≡〈k2〉/〈k〉=2,其中〈k〉代表平均节点度。
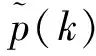
(5)
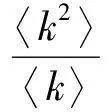
(6)
所以可以由pc来衡量拓扑的容错性,当m为定值时,拓扑的容错性随着幂率指数λ的增大而减小,所以要构造强容错性的拓扑就要maxpc。
1.2 问题分析
WSNs拓扑控制的主要目标就是在确保网络容错特性的前提下,兼顾抗毁性、网络生命期、负载均衡等性能,形成优化的网络拓扑[14],这样本文要解决的问题可以概括为:①最小化kmax,使得网络拥有较好的抵御蓄意攻击的能力,即minkmax。②最大化拓扑的容错能力,使得网络拓扑有较好的容忍节点失败的能力,即maxpc。
所以可以将本文的研究问题归结于建立一个兼顾minkmax和maxpc的WSNs无标度拓扑结构,由式(7)来描述
maxf=pc/kmax
(7)
2 BAEM算法
为了演化出对随机节点移除和选择性节点移除有综合容错性的WSNs无标度容错拓扑结构,可以借助文献[15-16]构建的无标度网络模型,此模型介于BA模型和随机网络之间,所以存在最优的无标度拓扑结构具有较好的容错性并能够提高选择性节点移除的能力。
2.1BAEM算法
①增长性:以少量个m0节点开始,在每一时间步长,向存在网络中加入一个新节点n,同时加上从此节点出发的m条边;
②择优连接:在择优增长时,新节点n仅在其传输范围内选择连接节点i,且此时的择优连接概率为
(8)
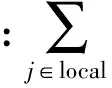
2.2BAEM拓扑算法动态特性分析
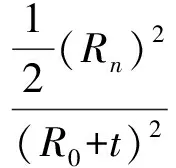
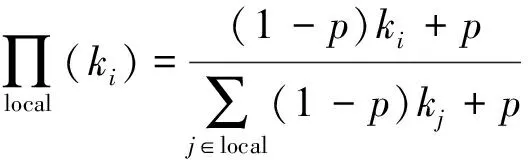
(9)

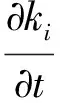
(10)
采用分离变量法并结合初始条件ki(ti)=m解上述微分方程可得
(11)
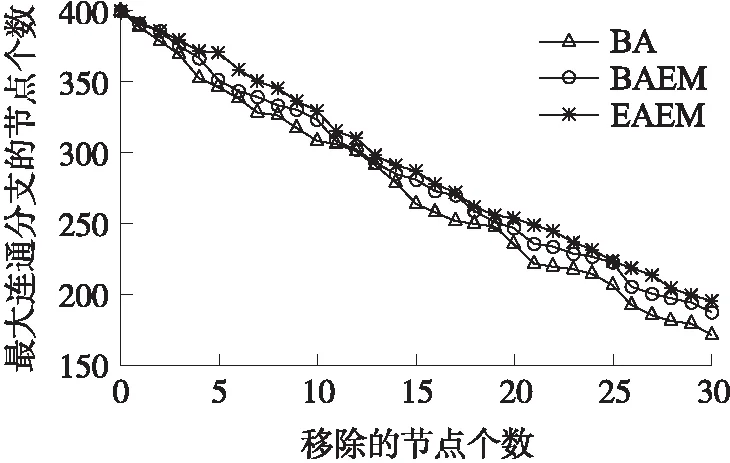
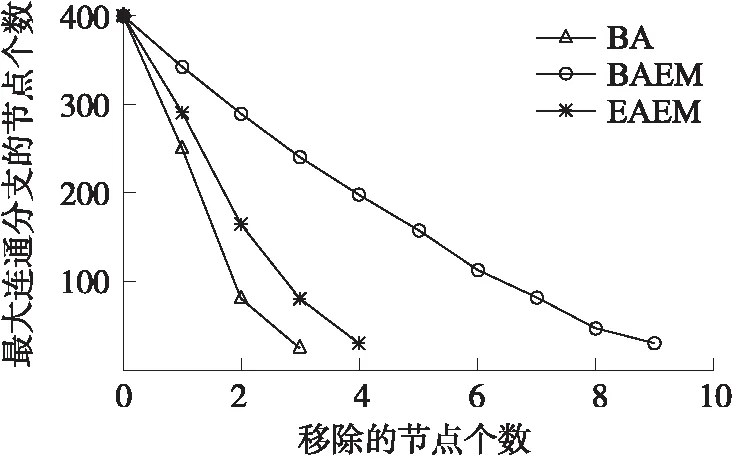
从而,节点i的度小于k的概率p(ki(t) (12) (13) 考虑到在改进的择优增长过程中,每一个时间步长仅有一个新节点加入到网络中,因此,ti服从均匀分布,其概率密度满足如下条件 (14) 结合式(14)和式(15)可得,经改进的择优增长过程演化出的容错拓扑BAEM的度分布表达式,如式(16)所示 (15) 由式(15)可见,在增长规模m给定后,演化拓扑BAEM近似为标度指数为λ=3+b的无标度网络,通过调节参数p可以使标度指数在[3,+∞)内变化。当p=0时,BAEM的度分布近似于p(k)~k-3,为标准的BA无标度网络模型,对随机节点移除行为有强容错性;当p=1时,BAEM的度分布近似为p(k)~e-k/m,网络无偏好倾向,为随机网络模型,可有效抵御选择性节点移除现象。 由于目前对于WSNs无标度拓扑容错算法的研究多集中于能源效率的优化,同时考虑网络容错和抗攻击抗毁能力的算法还不常见,为此,本文针对具有节能代表性的EAEM算法和经典的BA算法进行MATLAB2012a仿真实验对比。在仿真实验中,3种算法采用了相同的初始网络规模和节点总数,其中,每一次实验都是50次实验的平均值,如表1所示。 表1 实验环境参数 3.1 拓扑容错性和抗毁性对比 为了衡量BAEM优化拓扑的容错能力和抗毁能力,将BA模型、EAEM算法拓扑模型和BAEM优化算法拓扑模型进行仿真对比,分别按随机删除和按节点度从大到小的顺序删除节点,然后分别统计网络中最大连通片分支上的节点数目,得到的容错抗毁对比图如图2和图3所示。 图2 容错对比图 图2为拓扑对随机失效的容忍能力比较图,有仿真图可知,BAEM算法拥有BA算法和EAEM算法几乎相同的容错性,这表明,BAEM算法继承了无标度网络强容错性的特点。图3为拓扑对恶意攻击的容忍能力比较图,由图中可以看出BAEM优化算法对恶意攻击的容忍能力明显高于EAEM算法和BA算法,BA算法和EAEM算法在选择性移除3到4个节点时,网络就处于瘫痪状态,而BAEM能承受将近9个节点的攻击。综上所述,BAEM算法生成的网络拓扑,不仅对节点随机失效有较好的容忍能力,而且对拓扑的蓄意攻击有较好的容忍性。 图3 抗毁对比图 3.2 网络生命期对比 由于传感器节点能量受限,最大限度的延长网络生命期成为构造WSNs拓扑的另一目标。分别运行上述3种算法,并记录不同节点失效比例下的网络生命期。每一轮试验中,各个节点与其邻居节点进行数据交换,依据低功耗无线通信能量消耗模型[13],运行BAEM优化算法、EAEM算法和BA算法,图4显示了在不同失效节点比例下(首节点,10%,30%,50%,70%,80%)网络生命期的对比情况。 图4 生命周期对比 从图4中可以看出,EAEM算法和BAEM优化算法所得拓扑在出现首节点失效时就相差较大,随着节点失效比例的增加,BAEM算法的网络生命期提升幅度越来越大,这主要是由于BAEM算法在构建拓扑时综合考虑了最大节点度和拓扑的容错性,限制了最大节点度,从而使节点的能耗更加均衡,提高了网络的生命期。 本文提出了一种新的无标度拓扑演化算法BAEM,并通过优化指标计算出最优拓扑参数。对BAEM优化算法与BA算法和EAEM算法进行仿真对比分析,BAEM算法具有强容错性,并能提高网络的抗毁能力,而且能够延长网络的生命期。利用BAEM优化算法,仅通过改变算法参数信息就可以产生满足特定网络性能需求的容错拓扑结构,为综合性能优化的无线传感器网络容错拓扑设计奠定了良好的基础。 [1] Li X Y,Wan P J,Wang Y,et al. Fault Tolerant Deployment and Topology Control in Wireless Ad Hoc Networks[J]. Wireless Communications and Mobile Computing,2004,4(1):109-125. [2] 王宁,周圆,刘敬浩. 一种基于改进粒子群的无线传感器网络层次化聚类协议[J]. 传感技术学报,2017,30(1):120-125. [3] Thallner B,Moser H,Schrnid U. Topology Control for Fault-Tolerant Communication in Wireless Ad Hoc Networks[J]. Wireless Networks,2010,16(2):387-404. [4] Jia Xiaohua,Dongsoo Kim,Sam Makki,et al. Power Assignment fork-Connectivity in Wireless Ad Hoc Networks[J]. Journal of Combinatorial Optimization 9.2,2005:213-222. [5] Li X L Feng D L,Peng C C. A Potential Game Based Topology Control Algorithm for Wireless Sensor Networks[J]. Acta Physica Sinica,2016,65(2):028401. [6] Jiang Lurong,Jin Xinyu,Xia Yongxiang,et al. A Scale-Free Topology Construction Model for Wireless Sensor Networks[J]. International Journal of Distributed Sensor Networks,2014,Article ID 764698. [7] Yao Hongxing,Tang Yu. Topology Evolving Model with Scale-Free Property for Wireless Sensor Networks[J]. International Journal of Nonlinear Science,2013,16(1):82-86. [8] 杜巍,蔡萌,杜海峰. 网络结构鲁棒性指标及应用研究[J]. 西安交通大学学报,2010,44(4):93-97. [9] Zhu H L,Luo H,Peng H P,et al. Complex Networks-Based Energy-Efficient Evolution Model for Wireless Sensor Networks[J]. Chaos,Solitons and Fractals,2009,41(4):1828-1835. [10] Qi X Q,Ma S Q,Zheng G Z. Topology Evolution of Wireless Sensor Networks Based on Adaptive Free-Scale Network[J]. Journal of Information and Computational Science,2011,8(3):467-475. [11] Solé Ricard V,Sergi V. Information Theory of Complex Networks:On Evolution and Architectural Constraints[J]. Complex Networks,2004:189-207. [12] Wang Bing,Huanwen Tang,Chonghui Guo,et al. Optimization of Network Structure to Random Failures[J]. Physica A:Statistical Mechanics and its Applications 2006,368(2):607-614. [13] 吴俊,谭跃进,邓宏钟,等. 标度指数不大于2的无标度网络的若干性质[J]. 系统科学与数学,2008,28(7):6. [14] Cohen,Reuven,DBen-Avraham,et al. Breakdown of the Internet Under Intentional Attack[J]. Physical Review Letters,2001,86(16):3682-3685. [15] Liu Zonghua,Ying Chenglai,Nong Ye,et al. Connectivity Distribution and Attack Tolerance of General Networks with Both Preferential and Random Attachments[J]. Physics Letters,2002,A303(5):337-344. [16] Xi W B,Xian E M,Chen Y G. Load Balancing for Wireless Sensor Networks Based on an Equiprobable Routing Model[J]. Journal of Electronics and Information Technology,2010,32:1205-1211. TopologyControlAlgorithmBasedonScale-FreePropertyinWirelessSensorNetworks* LIUZhouzhou*,LIWenwei (Xi’an Aeronautical University Sensor network and Intelligent Computing Lab,Xi’an 710077,China) The issue that the WSNs are vulnerable with deliberate attacks is studied,and a new scale-free network evolution model(BAEM)is proposed. And then through analyzing the effect of the power-law exponent on network intrusion-tolerance and topology fault-tolerance,the optimal topology is derived which can assure the topology fault-tolerance and maximize topology intrusion-tolerance. The simulation results show that new fault-tolerant topology can keep the character that the scale-free network model has stronger robustness to random failures,and it also can reduce their fragility against intentional attacks and provide longer network lifetime. wireless sensor networks;scale-free;intrusion-tolerance;fault-tolerance A 1004-1699(2017)10-1578-05 10.3969/j.issn.1004-1699.2017.10.021 刘洲洲(1981-)男,汉族,陕西延安人,博士,副教授,主要研究方向为无线传感器网络,liuzhouzhou8192@126.com。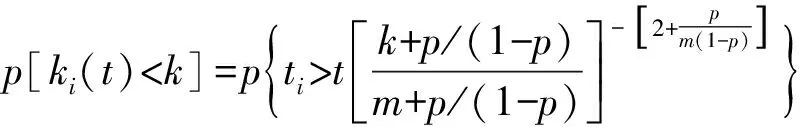

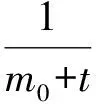
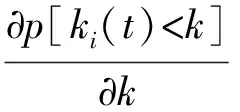
3 仿真分析

4 结论


