HERTZ型与非HERTZ型接触理论计算方法
杨咸启,钱胜,褚园,刘胜荣
(黄山学院机电工程学院,安徽黄山245041)
HERTZ型与非HERTZ型接触理论计算方法
杨咸启,钱胜,褚园,刘胜荣
(黄山学院机电工程学院,安徽黄山245041)
Hertz型接触和非Hertz型接触理论涉及的计算过程比较繁杂,因此,针对一般的Hertz接触问题,通过理论分析,给出了接触曲率比函数与接触椭圆偏心率以及椭圆积分之间的关系。利用接触曲率比函数直接计算出接触参数率,使得接触计算变得相对简化。同时,建立了非Hertz接触参数的近似模型。
Hertz型接触;非Hertz型接触;曲率比函数;椭圆偏心率;计算方法
1 概述
工程中经常会遇到两个构件相互接触,并且承受比较大的载荷。例如,火车轮轨接触、齿轮啮合接触、轴承零件内部接触,等等。因此,需要计算接触部位的应力。这些接触问题多数是属于弹性Hertz接触问题,也即是在微小接触区域上的微小弹性变形接触问题。计算接触应力时需要采用Hertz接触理论。首先要利用接触表面的曲率系数,再计算椭圆积分函数,这个过程往往比较复杂。
从初始接触状态的不同,接触类型通常分为点接触和线接触。如果两个物体开始接触时只有一点的情况称为点接触,如果两个物体开始接触时是一条线的情况称为线接触。这些接触通常都作为Hertz型接触问题,Hertz问题的求解的前提假设为:
1.接触体的材料处于弹性状态;
2.接触区域表面是理想光滑的二次曲面,不考虑摩擦;
3.接触面尺寸与弹性体表面的曲率半径尺寸相比是很小的量;
4.接触压力分布模式与接触区域形状与接触表面相适应。
在这些假设条件下,可以求解出接触问题的理论解。下面分别介绍点接触和线接触的计算方法[1-7]。
2 Hertz型点接触参数
2.1 球面体点接触
当两个光滑的球面体在外力Q作用下相互接触,如图1所示。
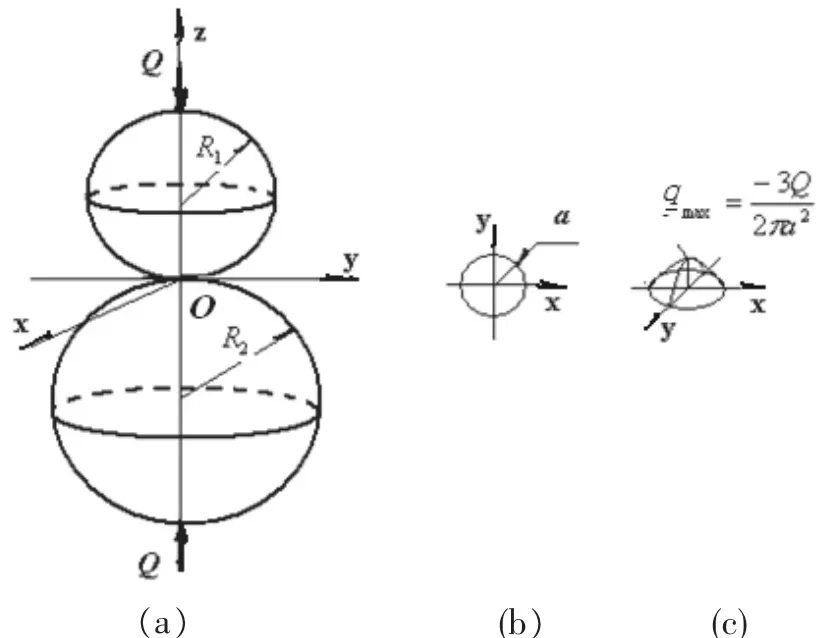
图1 球体点接触模型
这是一种典型的点接触情况,由于球体的对称性,明显的,接触区域为半径为a的圆(如图1(b)为接触区域放大图)。圆的方程可以写为r2=x2+y2=a2。接触区上的接触压力分布与接触区域点的位置有关,在接触区域中心点接触压力最大,在边缘点上接触压力为零。因此,为了与接触表面相适应,Hertz解假定接触压力分布为半椭球面分布

式中,qmax为最大接触力,a为接触区半径,r为极径坐标。求解接触问题关键就是确定接触区半径a和最大接触压qmax。
由外力与接触力的平衡条件,并且利用半椭球体的体积积分得到
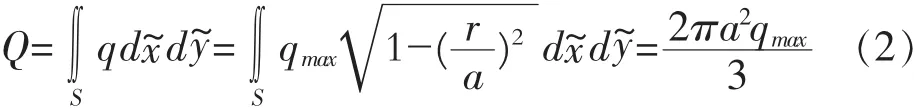
所以,最大接触压力为

由于接触发生在很小的区域,外力分布在接触区上,可以将这样的问题当作为半无限大体上作用一个很小的分布力问题的Boussinesq解来处理。因此,经过推导得到接触区的参数为

式中,R1、R2为球面半径,δ为接触原点上两个球体的变形之和(也称为两球体的弹性变形趋近量δ)。称为当量弹性模量。
2.2 二次曲面体点接触
对于任意光滑曲面体,在外力Q作用下相互对中接触在一起,如图2(a)所示。在满足Hertz假设条件情况下,这个问题可以得到完整的理论解。实际上,在微小的接触面上,任意曲面总可以近似表达为二次曲面而具有足够的精确性。下面来求解一般的曲面体的Hertz型接触问题。
同前面一样,建立接触区域坐标系,选择初始接触点为坐标系原点。以接触点的切平面为xy平面,z轴指向体内部。
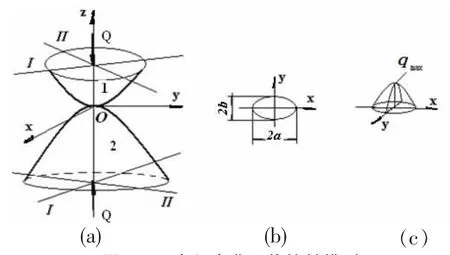
图2 两个任意曲面体接触模型
Hertz解认为接触区域应该是椭圆形区域(图2(b)为接触区域放大图)。椭圆的方程可以写为(x/a)2+(y/b)2=1,a、b为椭圆半轴长。椭圆形区域为

接触区上的接触压力分布与接触区域点的位置有关,在接触区域中心点压力最大,在边缘点上压力为零。因此,为了与接触表面相适应,Hertz解假定接触压力分布是一种半椭球的形状(图2(c)),即
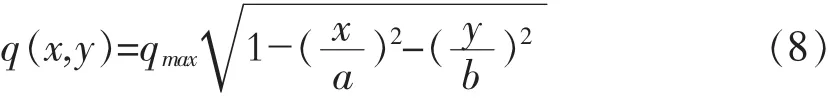
其中,qmax为最大接触压力。这是一种半椭球方程。求解接触问题就是确定接触区半径a、b和最大接触压qmax。
由接触压力与外力的平衡关系,并且利用半椭球体的体积积分得到
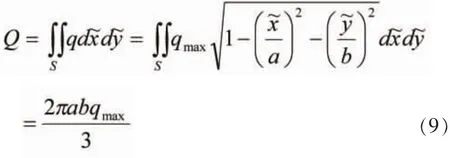
所以,最大接触压应力为

利用半无限大体上作用一个很小的分布力问题的Boussinesq解,经过积分简化计算后得到接触区域参数为

到此,一般的Hertz型接触问题的理论解就确定出来了。但是具体的计算还需要求椭圆积分,其过程还是比较复杂的。
接触区域各量的计算过程是已知接触表面的主曲率后,首先计算出接触表面曲率比函数
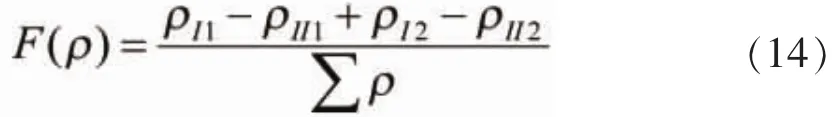
再定出接触椭圆偏心率e

进一步,计算出第一、二类完全椭圆积分Γ(e)、Π(e)以及计算a*、b*、δ*。但这个过程比较复杂。实际中是先给定参数e计算出Γ(e)、Π(e),再计算F(p),将计算结果制成图表。在工程问题计算时,反过来利用已经计算好的参数表,利用直接查和插补计算方法来快速近似计算[7-9]。
上面给出的接触参数计算公式比较复杂,实际应用中不太方便。下面介绍新的近似计算方法,根据接触表面曲率函数F(p)与来确定椭圆参数e和椭圆积分。
在式(15)中,关系比较复杂,对参数e趋近于零时是一种不定式。为了避免这种不定式计算,本文利用接触体的表面曲率比函数F(p)来近似计算接触参数的方法如下。


3 二维弹性体线接触参数
当两个光滑的圆柱体长度相同为l,或为无限长,轴线平行,在外力Q作用下对中接触,如图3(a)所示。这是一种理想的线接触情况,这时接触区域为矩形(如图3(b)所示接触区域放大图)。沿轴线的接触压力分布为均匀分布。这样,它可以转化为平面接触问题。对无限长线接触对应于平面应变问题,对相同长度的线接触对应于平面应力问题。
在Hertz假设条件下也可以获得二维弹性体接触压力分布等结果。

图3 两个长度相同圆柱体线接触模型
设接触圆柱体的半径为R1、R2,材料弹性模量和泊松比分别为E1、ν1;E2、ν2。类似于点接触的分析方法,为了与接触表面相适应,Hertz解假定接触压力分布为半椭圆柱体(图3(b)所示接触压力示意图,接触区域为矩形,2bXl)

由外力与接触力的平衡条件,并且利用半椭圆柱体的体积积分得到

因此,得到接触表面的最大压力为

但是,线接触不能严格导出弹性体的趋近量。而K.L.Johson利用平面应力与应变状态积分,得出两个圆柱体接触区中心弹性趋近量近似公式为[1]

式中,Q为作用外力,l为接触圆柱体长度,R1、R2分别为接触圆柱体的半径,b为接触区域半宽度,E1、ν1;E2、ν2分别为材料弹性模量和泊松比。
而A.Palmgren通过试验给出带凸度的圆柱体接触中心弹性趋近量的近似公式为[3]


文献[11,12]中提出一种近似的线接触变形趋近量计算公式为

4 非Hertz型接触参数计算
如果在接触分析中放弃Hertz假设,则称为非Hertz接触问题。通常分为两类情况,一类是接触表面为非光滑曲面,另外一类为大接触表面。由于非Hertz接触问题要复杂很多,很多问题还没有理论解。下面介绍几个典型的非Hertz接触问题模型[10-13]。
4.1 有限长线接触
当两个圆柱体长度不相同,而轴线平行地相接触,或一个有限长的圆柱与无限大平面接触,这样就称为有限长线接触。如图4所示。他们在工程问题中经常会遇到。

图4 有限长线接触模型
有限长线接触没有理论解,在圆柱体端部边界会出现应力集中现象。求解有限长线接触问题通常采用数值方法[10]。在接触区域,划分微小单元,利用数值积分求出下面的接触变形

再利用接触变形协调条件和平衡方程
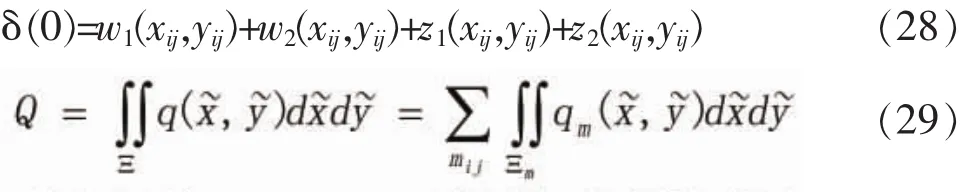
可以建立一组方程。求解方程组(26)-(28)得到接触区域上的压力分布。在求解过程中,首先假定接触区域的大小,同时,必须保证接触压力为非负值(qm≥0)。
图5(a)为有限长线接触示意图。图5(b)、(c)为有限长线接触的变形和接触应力分布情况,在圆柱的端部出现了明显的应力集中[3]。
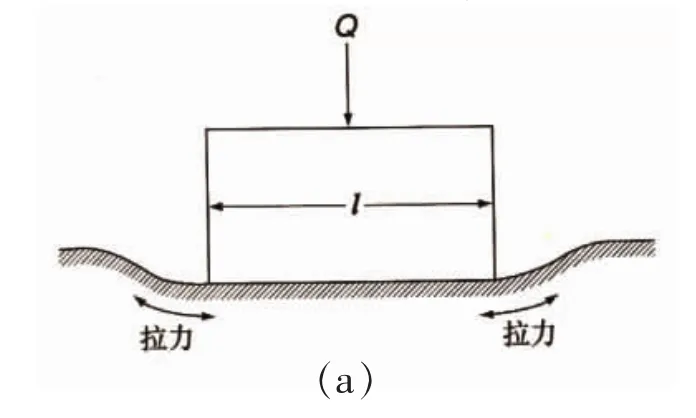
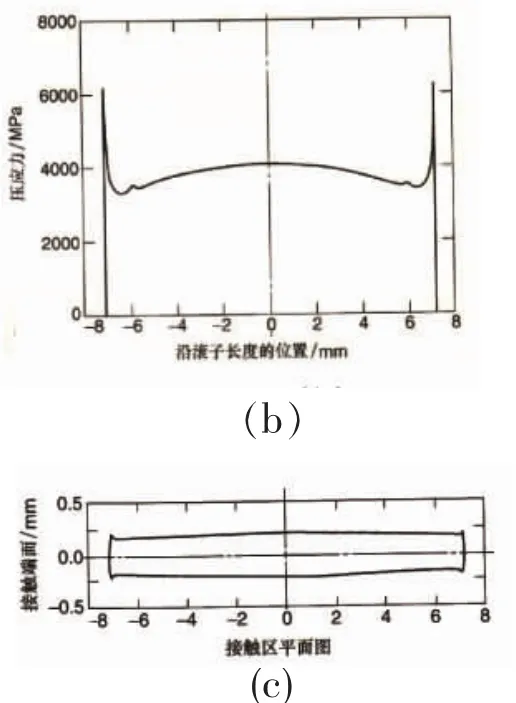
图5 有限长圆柱线接触
4.2 曲面非对中接触与非主曲率平面接触
对于光滑曲面体非对中接触问题,如图6(a)所示。或非主曲率平面的接触问题,如图6(b)所示。他们在工程问题中有时也会遇到。

图6 接触模型
在弹性状态下,本文假设这种接触问题产生的接触区域为

根据接触压力分布必须与接触区域相适应的原则,假设接触区域上的压力分布为

其中,q0为接触压力特征值,通过选择不同的指数α来反映曲面的特点。
接触力的平衡条件为

而接触变形的协调条件可以写成
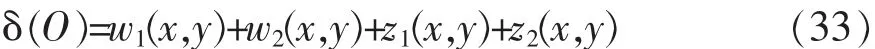
上式中,δ(O)代表接触原点上两个球体的变形之和(也称为两体的弹性变形趋近量δ),w1,w2为两个接触表面的变形,且

在小变形的情况下,接触变形的协调条件也可以写成
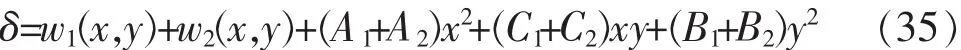
同样也可以利用半无限大平面上受分布力作用的变形计算方法(Boussinesq解),

上面的积分需要在已知压力分布函数的情况下才可以进行。多数情况下需要利用数值积分方法求解,如同有限长线接触的计算过程。
4.3 非光滑曲面接触
两个非光滑表面受压力作用而接触形式如图7所示。假设接触区域边界方程为


图7 非光滑表面接触模型
本文假设接触区域上的压力分布为

其中,q0为特征接触压力,β为指数,C为常数,Z1、Z2为接触体非光滑表面坐标。
对于非光滑表面,K1(H1,H2)、K2(H1,H2)为与接触体材料硬度H1,H2有关的接触变形分配系数,

材料硬度越大,接触变形越小,因此,假设变形分配系数与硬度之间存在反比的关系

由接触压力与外载荷的平衡关系
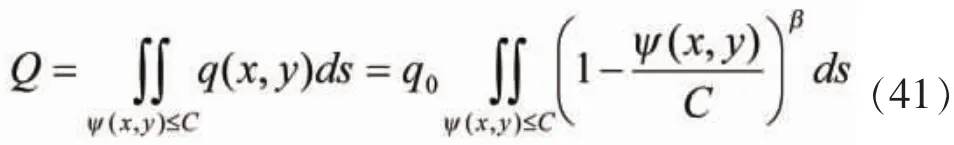
考虑到非光滑表面的材料特性,上面的积分中
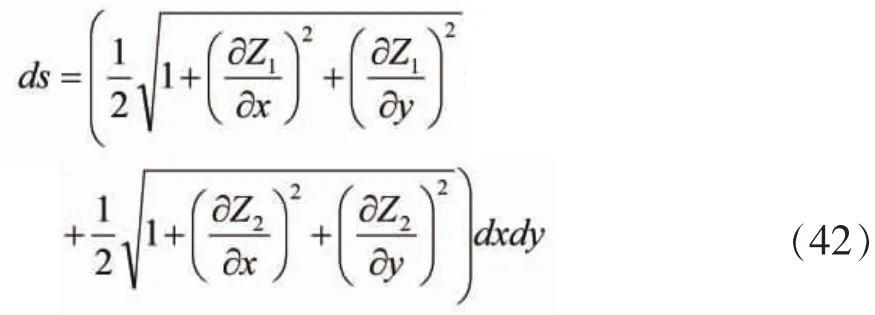
如果接触表面的变化是平缓的,则有
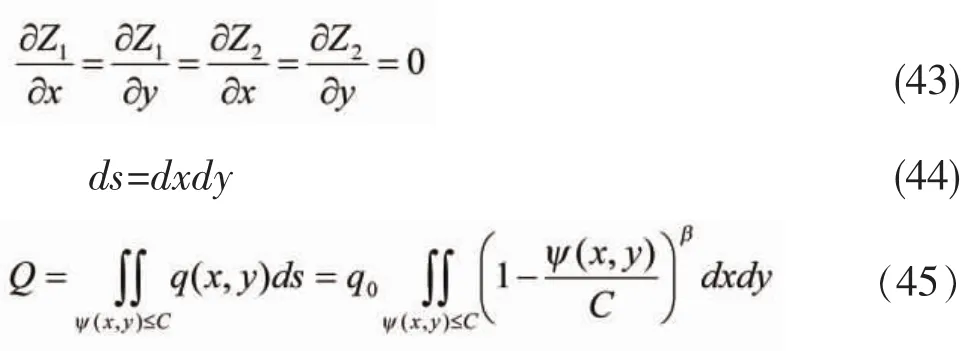
以上的公式是非光滑表面的接触压力的简化计算方法。
而非光滑表面的接触变形大多数会出现塑性变形,计算这种塑性变形非常复杂,需要建立更复杂的模型。这方面已经有不少的研究者给出了有意义的结果。
5 总结
本文介绍了Hertz型点接触理论的分析结果,将接触参数的计算过程进行了简化,满足工程设计中应用要求。同时,对非Hertz型接触的典型问题进行了理论分析。得到的主要结果为
1.拟合出点接触曲率比函数与接触椭圆率e、椭圆积分的关系函数,省去了复杂的计算过程,使得接触计算变得相对简化。
2.建立了非Hertz型接触模型参数的近似计算方法。
[1]K.L.Johnson Contac Mechanics[M].Cambridge University Press,1985:5-150.
[2]L.C.Wrobei,C.C.A.Brebbia,AxisymmetricPotential Problems,New Development in Boundary Element Method[M].Cml Publications Limited 125 High Street Southampton SO10AA,1980:201-230.
[3]T.A.Harris Rolling Bearing Analysis(3rd)[M].John Wiley&Sons Inc.,1991:30-98.
[4]钱伟长,叶开沅.弹性力学[M].北京:科学出版社,1956:297-326.
[5]加林.弹性理论的接触问题[M].北京:科学出版社,1958:262-265.
[6]皮萨连科,亚科符列夫,马特维也夫.材料力学手册[M].北京:中国建筑工业出版社,1981:630-650.
[7](德)瓦伦丁L.波波夫.接触力学与摩擦学的原理及其应用[M].北京:清华大学出版社,2011:1-30.
[8]杨咸启,刘胜荣,褚园.轴承接触应力计算与塑性屈服安定[J].轴承,2015,(3):7-10.
[9]杨咸启,刘胜荣,曹建华.HERTZ接触应力强度问题研究[J].机械强度,2016,38(3):580-584.
[10]马家驹,三维有限长弹性接触问题的数值解[C].洛阳:洛阳轴承研究所,1984:1-9.
[11]丁长安,等.线接触弹性接触变形的解析算法[J].摩擦学学报,2001,21(2):135-138.
[12]丁长安,等,滚子轴承受载变形计算的修正[J].轴承,2007(8):1-4.
[13]刘法炎,接触应力计算的改进方法[J].河南城专学报,1992(1):28-42.
The Calculation Method of Hertzian and Non-Hertzian Contact Theory
Yang Xianqi,Qian Sheng,Chu Yuan,Liu Shengrong
(School of Mechanical and Electrical Engineering,Huangshan University,Huangshan 245041,China)
The calculation process involved in Hertzian contact and non-Hertzian contact theory is very com plicated.In this paper,for the general Hertzian contact problem,the relation between the contact curvature ratio function and the contact ellipse eccentricity as well as the elliptic integral is given by theoretical analysis.The contact parameters are calculated directly by the contact curvature ratio function,which relatively simplifies con tact calculation.And an approximate model for non-Hertzian contact parameters is also established.
Hertzian contact;non-Hertzian contact;curvature ratio function;elliptic eccentricity;calcula ion method
TH114
A
1672-447X(2017)05-0013-006
2017-08-29
安徽省教育厅质量工程项目(2014zdjy122)
杨咸启(1957-),安徽枞阳人,黄山学院教授,研究方向为机械工程设计、轴承理论、摩擦学。
责任编辑:胡德明

