安徽省人口发展趋势预测——单一模型与组合模型的模拟仿真比较

杨世娟，李胜

（1.黄山学院数学与统计学院，安徽黄山245041；2.六安市第九中学，安徽六安237000）

安徽省人口发展趋势预测
——单一模型与组合模型的模拟仿真比较

杨世娟1，李胜2

（1.黄山学院数学与统计学院，安徽黄山245041；2.六安市第九中学，安徽六安237000）

选取安徽省2000-2015年户籍人口数年度数据作为样本，利用单一模型（Malthus模型、Logistic模型和灰色DGM(2,1)模型）及组合模型对安徽省人口发展趋势进行预测、比较与分析，结果表明基于组合模型的人口规模预测精度比单一模型的预测精度高，预测性能最好。利用组合预测模型预测了安徽省未来的人口数量，以期对安徽省未来的人口规模以及发展趋势做出合理的分析与判断。

人口预测；组合模型；Logistic模型；灰色DGM(2,1)

1 引言

预测指的是对先验信息进行分析，并通过建立相应模型，推测未来某事件是否会发生或事件的发展趋势。随着学术界不断的推陈出新，新的预测方法层出不穷，预测技术也变得越来越成熟，在将各种预测技术应用到具体的实践过程中时，往往会由于针对的问题迥异和先验信息的多寡，所适应的模型并不相同，且这些模型并非预测精度都高，需各方面综合考虑选取“最优”的模型，但这简单依靠一种模型往往难以达到。如果能综合这些模型，充分利用各模型优势，用适当的方法加以重组，便可得到一个精度更高的模型[1]。组合预测模型就是从这一角度出发的，它充分利用各个单一模型的信息，降低各个单一模型受到的随机影响，因此组合预测模型能汲取各个模型的优点，提高模型整体的预测精度[2]。

人口问题既是一个社会问题，也是一个经济发展问题，历来都受到各个国家和地区的关注。相对于其他经济大省，安徽省的经济欠发达，而人口众多，且人口的发展具有显明的地方特点[3]。在现代化及城镇化进程中，要实现人口与经济、社会、环境的协调发展，有效地分析与科学地预测安徽省人口的发展变化趋势显得既紧迫又重要。

2 基于组合预测模型的安徽省人口发展趋势模拟

2.1 组合预测模型构建

假设安徽省人口规模的历史数据为Y=（y1,y2,…yn）T，n为时间跨度，现采用m种预测方法建立安徽省人口发展趋势的预测模型，并根据所建立的模型对历史数据进行模拟，设m种预测模型在时期t的模拟值为{f1（t），f2（t）,…，fm（t）}。组合预测模型采用加权的方式综合m种预测模型的优点，将综合值作为安徽省人口数量的最终模拟值，最终值为：

其中W={w1，w2，…，wm}为权重，且满足

2.2 权重的确定

在构建安徽省人口发展趋势组合预测模型的过程中，最关键的一步是确定权重向量W=（w1，w2，…，wm），依据模拟值与实际值之间的偏差尽可能小的原则来确定组合权重向量，即通过建立如下方程，利用多元函数极值原理求解得出权重向量[4]：

对（2）式关于自变量wj（j=1,2,…，m）求偏导，并令偏导为零，则可得到偏导数方程：

将（3）式进行变换与整理，可得如下方程组：

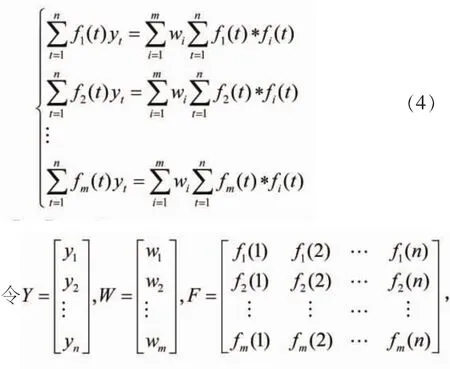
则（4）式可表示为：FY=FFTW

利用矩阵方程求解，即可得出组合预测模型中权重公式：

3 单一模型与组合模型的模拟仿真比较

以下实证分析所采用的预测技术涉及到的原始数据来自于2001-2016年的《安徽省统计年鉴》，表征人口发展规模的变量选取为安徽省户籍人口数，单位为万人，数据序列的时间跨度为2000-2015年。

综合考虑安徽省人口发展的典型特点以及实际预测需要，文中选取3种预测技术构建安徽省人口发展趋势预测的单一模型：Malthus模型、Logistic模型和灰色DGM(2,1)模型，并采用上述组合权重确定方法选取组合权重向量，整合单一模型的各自优势构建组合预测模型，以便充分利用各单一模型的信息，降低各单一模型受到的随机影响，提高整体的预测精度。

3.1 Malthus模型

英国统计学家Malthus在《人口原理》一书中首次提出了Malthus人口模型，模型的基本思想是在人口自然增长过程中，净相对增长是常数，即单位时间内人口的增长量与人口成正比，并设定比例系数设为r，在此假设下，推导并求解人口随时间变化的数学模型。Malthus人口模型认为人口以几何级数增长，故采用指数函数来拟合、预测人口增长[5]。具体建模步骤如下。

令y（t）表示t（t=0,1,2,…）时刻人口数量，y0表示初始时刻的人口数量，人口出生率为b，人口死亡率为c，假设人口自然增长率为r，则在t到t+△t时间段内人口的增量为：

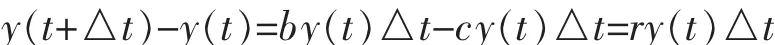
当△t→0时，满足如下微分方程：

模型的最终表达公式为：

利用Malthus预测模型对安徽省人口发展趋势进行建模，并利用所建立模型对2000-2015年人口规模进行拟合，将计算结果与实际数据做比较[6]。记Malthus模型估计的安徽省历年人口数量模拟值为y1，估计的相对误差为e1，具体数值见表1。估计的最终模型如下：

3.2 Logistic模型

Logistic模型也叫做阻滞增长模型，该模型考虑到自然资源与环境条件对人口数量有限制作用，认为一定环境所容纳的人口数量是一定的，人口不会无限制的增加，而是最终趋近于某个常数[7]。阻滞作用体现在对人口增长率的影响上，即r为关于y的减函数r（y）。一个最简单的假定是令r（y）为y的线性函数：

其中，r为人口的固有增长率，s=r/ym，ym为一定自然资源和环境条件下所能容纳的最大人口数量。于是可以建立如下微分方程：

解该方程，得到模型的最终表达形式为：

利用Logistic预测模型对安徽省人口发展趋势进行建模，并利用所建立模型对各年人口规模进行拟合，将计算结果与实际数据做比较。记Logistic预测模型估计的安徽省历年人口数量模拟值为y2，估计的相对误差记为e2，具体数值见表1。最终模型如下：

3.3 DGM(2,1)模型

灰色预测就是通过对原始数据的处理来发现并掌握系统发展的规律，并对系统的未来状态做出定量预测。它主要用于时间跨度短，历史数据少，波动性不大的预测问题，且对于序列较短而有规律的数据来说，灰色预测的精度较高[8]。人口数量的影响因素较多，包括确定因素与不确定的因素，适合于用灰色预测模型进行趋势估计。但GM(1,1)模型的应用前提是序列具有较强指数规律，对于非单调的摆动发展序列或饱和的S型序列并不适用，在这种情况下可以建立GM(2,1)或DGM模型代替之[9]。以下对安徽省2000-2015年的人口数据拟合灰色DGM(2,1)模型。

记安徽省人口规模的历史数据序列为

y（0）=（y（0）（1），y（0）（2），…，y（0）（n）），其1-AGO序列y（1）和1-IAGO序列α（1）y（0）分别为y（1）=（y（1）（1），y（1）（2），…，y（1）（n））和α（1）y（0）=（α（1）y（0）（2），α（1）y（0）（3），…，α（1）y（0）（n）），则DGM(2,1)模型为：

其白化方程为：

表1 安徽省历年人口规模及4种预测方法的模拟数值

DGM(2,1)模型的时间响应序列为：

经过一阶累减还原后的还原值为：

利用DGM(2,1)预测模型对安徽省人口发展趋势进行建模，并利用所建立模型对各年人口规模进行拟合。估计的结果如下：

DGM(2,1)时间响应函数为

做1-IAGO还原，得原序列的预测方程

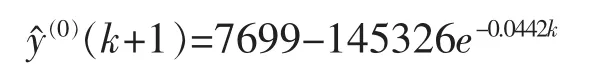
记DGM(2,1)模型下安徽省历年人口数量的模拟值为y3，估计的相对误差记为e3，具体数值见表1。

3.4 组合预测

利用前述组合预测模型模拟安徽省人口发展趋势，关键在组合权重的确定。首先利用前文推导出的组合权重确定公式W=（FFT）-1FY计算组合权重向量，计算结果为：

然后，通过组合预测模型计算人口数量的模拟值以及估计的误差，记安徽省历年人口数量的模拟值为y4，估计的相对误差记为e4，具体数值见表1。

表1给出了4种预测方法得到的模拟值和估计的相对误差，并与安徽省历年的人口数量原始数据进行了对比，较清晰的展示了各个方法的预测效果。为了更直观的展现对比效果，将真实值与4种预测方法的模拟值作图，并且对4种预测方法估计的相对误差进行图示，如图1与图2所示。

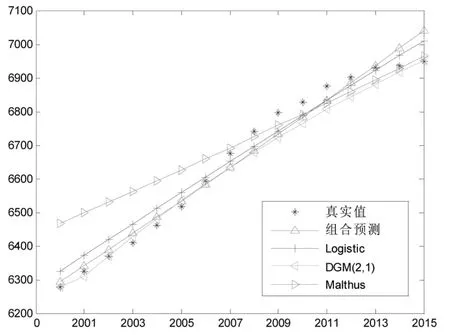
图1 真实值与4种预测方法拟合值

图2 4种人口预测方法的相对误差

通过对比与分析可以看出，4种人口发展趋势的预测模型中，组合预测模型估计的相对误差较其余3种单一模型的相对误差要小，表明组合预测方法能一定程度上提高模型的预测精度，体现出其在短期预测上的高效性。

鉴于组合预测模型的在短期预测上的高效性，现利用该模型对安徽省2016-2020年的人口数量进行预测，预测结果如表2所示。

表2 2016-2020年安徽省户籍人口数量预测值

4 结束语

人口问题关系到社会、经济、环境等各个方面的协调与可持续发展，对现在及未来人口的发展变化趋势做出合理、准确的分析与判断，对安徽省乃至整个国家来说都具有非常重要的意义。文章主要对安徽省的人口发展与变化趋势的预测做了更加精确的研究，以往的预测方法主要是采用单一的模型进行预测，虽然具有一定的预测精度，但考虑到安徽省人口发展的典型特点以及非线性的影响因素，所以不应该只限于某个单一的模型进行预测，而应该从不同的角度选用不同的预测技术构建模型，再运用适当的方法确定组合权重对各个预测结果进行综合加权，以便更好地利用各种预测技术的优势，进一步提高预测精度。文中采用了Malthus模型、Logistic模型、灰色DGM(2,1)模型构建了安徽省人口发展趋势预测的单一模型，并通过选取适当权重整合单一模型的各自优势构建组合模型。通过实例分析验证了基于组合预测模型的安徽省人口发展趋势预测的效果要优于单一模型的预测效果。

[1]蔚春杰.组合预测模型在CPI预测中的应用[D].大连：东北财经大学，2012：106-118.

[2]王淑花.基于时间序列模型的组合预测模型研究[D].河北：燕山大学，2011：45-78.

[3]黄立山.安徽省人口中长期发展战略[C].全国统计科学讨论会，2005:484-491.

[4]余路.电信客户流失的组合预测模型[J].华侨大学学报:自然科学版，2016(5)：637-640.

[5]刘志佳,黄河清.土地资源对珠三角地区人口增长的约束分析[J].生态环境学报，2014，23(12)：2003-2009.

[6]潘黎霞.基于微分方程模型的我国出口贸易实证研究[J].统计与决策，2011(20)：120-122.

[7]李勇胜.人口预测中的模型选择与参数的认定[J].财经科学，2004(2)：68-72.

[8]杨世娟,卢维学,方辉平.灰色系统与BP神经网络组合模型及其应用[J].统计与决策，2016(24)：82-84.

[9]邓聚龙.灰理论基础[M].武汉：华中科技大学出版社，2002:21-36.

The Prediction of Population Development Trend in Anhui Province——A Comparison of the Single Models and Combined Model

Yang Shijuan1,Li Sheng2
(1.School of Mathematics and Statistics,Huangshan University,Huangshan245041,China;2.Mathematics Group,Lu'an Ninth Middle School,Lu’an237000,China)

Selecting the annual data of the registered population in Anhui Province from 2000 to 2015 as the sample,the population development trend is forecasted,compared and analyzed based on the single models(Malthus model,Logistic model and DGM(2,1)model)and the combined model.Result of the research reveals that the accuracy of the prediction based on the combined model is higher than that of the single models,and the prediction performance is the best.Finally,the future population of Anhui Province is forecasted by using the combined forecasting model,so as to make a reasonable analysis and judgment on the future population size and development trend of Anhui Province.

population prediction;combined model;Logistic model;DGM(2,1)

F222；C812

A

1672-447X(2017)05-0001-005

2017-06-03

安徽省教育厅自然科学研究项目（KJHS2016B04；KJHS2017B09）；安徽省大学生创新创业训练计划项目（201510375019）；黄山学院自然科学研究项目（2015xkj004；2015xkj005）

杨世娟(1988-)，安徽安庆人，硕士，黄山学院数学与统计学院助教，研究方向为应用统计；李胜(1964-)，安徽六安人，六安市第九中学高级教师，研究方向为数学教育。

责任编辑：胡德明