稻谷堆的修正莱特-邓肯模型参数研究

杜小翠 程绪铎 高梦瑶 冯家畅(南京财经大学食品科学与工程学院/江苏省现代粮食流通与安全协同创新中心,南京 210046)

稻谷堆的修正莱特-邓肯模型参数研究

杜小翠 程绪铎 高梦瑶 冯家畅
(南京财经大学食品科学与工程学院/江苏省现代粮食流通与安全协同创新中心,南京 210046)

使用TSZ-6A应变控制式三轴仪对4个不同含水率的稻谷堆进行轴向压缩试验和各向等压压缩试验，由试验数据计算出稻谷堆的修正莱特-邓肯模型的14个参数。试验结果表明：含水率为12.35%、13.68%、15.09%、16.52% w.b.稻谷堆的弹性模量数K分别为167.65、182.98、196.79、199.66，弹性模量指数n分别为0.80、1.17、1.10、0.96，泊松比ν分别为0.204、0.214、0.221、0.268；塑性塌落模量C分别为0.001 2、0.002 7、0.001 0、0.002 3，塑性塌落指数p分别为1.53、1.37、1.64、1.30；塑性剪切屈服常数η1分别为223.31、382.82、207.59、494.54，塑性剪切屈服指数m分别为0.58、0.93、0.76、1.14，势参数S分别为0.334、0.398、0.351、0.306，势参数R分别为1.447、8.330、0.811、-2.016，势参数t分别为2.26、1.07、1.79、2.74，硬化功参数θ分别为0.53、0.48、0.45、0.47，硬化功参数l分别为0.67、0.55、0.63、0.49，硬化功参数α分别为0.30、0.09、0.09、0.12，硬化功参数β分别为0.08、0.28、0.25、0.16。且K、ν随含水率的增大而增大，ν随围压增大而减小，其他参数与含水率无显著性关系。

稻谷堆 修正莱特-邓肯模型 模型参数

自20世纪70年代以来，人们开始用有限元法研究筒仓中物料的应力应变分布问题[1]。Jofriet等[1]采用线弹性模型，用有限元方法研究了直筒仓内物料静态时的应力分布问题。Bishara[2]使用非线性弹性模型，用有限元方法估算了混凝土仓的静态仓壁压力。Ooi等[3]将散体假定为弹性体，使用有限元方法研究了柔性筒仓内散体的应力分布。一些国内的研究者采用多种本构方程使用有限元方法研究了筒仓中物料的应力应变分布问题[4-7]。这些研究很好地给出了储藏在筒仓中压缩性很小的沙子、碎石、工业物料的应力分布，以上研究所使用的本构方程假定物料的体积变化很小且发生在弹性变形阶段，形状变化发生在塑性变形阶段，在塑性变形阶段无体积变化。稻谷与土壤、沙子、工业物料的力学特性有很大的差异，稻谷籽粒松软，稻谷堆的孔隙率大。稻谷堆受压时体积变化大且体积变化发生在弹性变形和塑性变形阶段，稻谷的弹性变形和塑性变形是分不开的[8-11]。因此，以上采用的本构方程不能用来研究筒仓中稻谷的应力应变分布问题。

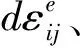
1 修正莱特-邓肯模型

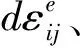
(1)

1.1 弹性应变分量

弹性应变分量可按三维胡克定律得到，即

(2)

弹性模量矩阵为：

(3)

式中：μ为泊松比；Eur为粮堆的加卸载弹性模量/kPa,即

Eur=K·Pa·(σ3/Pa)n

(4)

式中：K为弹性模量数,无量纲；n为弹性模量指数,无量纲；Pa为大气压/kPa；σ3为最小主应力/kPa。

1.2 塑性塌落应变分量

塑性塌落应变是由平均正应力引起的,卸载时,此应变不恢复,塌落特性由屈服函数控制。

Fc=fc-Kc

(5)

(6)

(7)

式中：I1=σ1+σ2+σ3；I2=-σ1σ2-σ2σ3-σ3σ1；Fc为塑性塌落屈服函数,量纲为F2/L4；fc为塑性塌落加载函数，量纲为F2/L4；Kc为塑性塌落功硬化函数，量纲为F2/L4；Wc为单位体积塑性塌落功,量纲为F/L2；C为塌落模量，无量纲；p为塌落指数，无量纲。

屈服面fc扩大，粮堆体积压缩，fc屈服面不会导致粮堆破坏。如果Fc=0，即fc=Kc，且dFc>0，产生塑性塌落应变，应变按相关联流动法则来计算：

(8)

gc=fc

(9)

式中：gc为塑性塌落势；dλc为微分正算子,按式(10)计算：

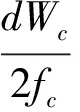
(10)

(11)

1.3 塑性剪切应变分量

塑性剪切应变是剪切应力引起的，是不可恢复的，塑性剪切特性由屈服函数控制：

Fp=fp-Kp

(12)

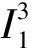
(13)

Kp=a·e-bWp(Wp/Pa)1/q

(14)

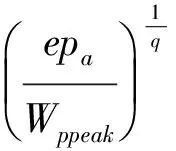
(15)

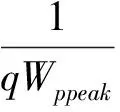
(16)

(17)

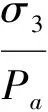
(18)

式中：Fp为塑性剪切屈服函数，无量纲；fp为塑性剪切加载函数，无量纲；Kp为塑性剪切功硬化函数，无量纲；η1为屈服常数，无量纲；α,β,θ,l为功硬化常数，无量纲；I3为第三应力不变量，I3=σ1σ2σ3，量纲为F3/L6；Wp为单位体积剪切功，量纲为F/L2；Wppeak为在点fp=η1的剪切功，量纲为F/L2；a,b,q为中间变量。

在任何加载和卸载阶段，如果Fp=0，即fp=Kp，且dFp>0，产生塑性剪切应变，应变按非相关联流动法则计算：

(19)

dλp，gp按公式计算

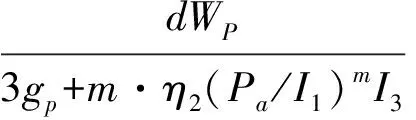
(20)

(21)

(22)

式中：dλp为微分正算子；gp为塑性剪切势；S,R,t为塑性剪切势常数。

粮堆破坏由fp控制，在fp=η1时，粮堆破坏。

1.4 本构方程

结合式(1)、式(2)、式(8)、式(19)，粮堆的应力与应变本构方程：

dσij=[Eep]dεij

(23)

(24)

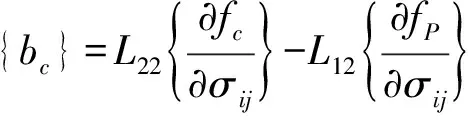
修正莱特-邓肯模型的本构方程中有14个参数，分别为弹性模量数K、弹性模量指数n、泊松比ν、塑性塌落模量C、塑性塌落指数p、塑性剪切屈服常数η1、塑性剪切屈服指数m、势参数S、R、t、硬化功参数θ、l、α和β。

2 本构方程参数测定

2.1 试验材料

淮稻5号稻谷，产地江苏淮安，原始含水率为13.68% w.b.，将稻谷含水率调节为：12.35%、13.68%、15.09%、16.52% w.b.。

2.2 试验仪器

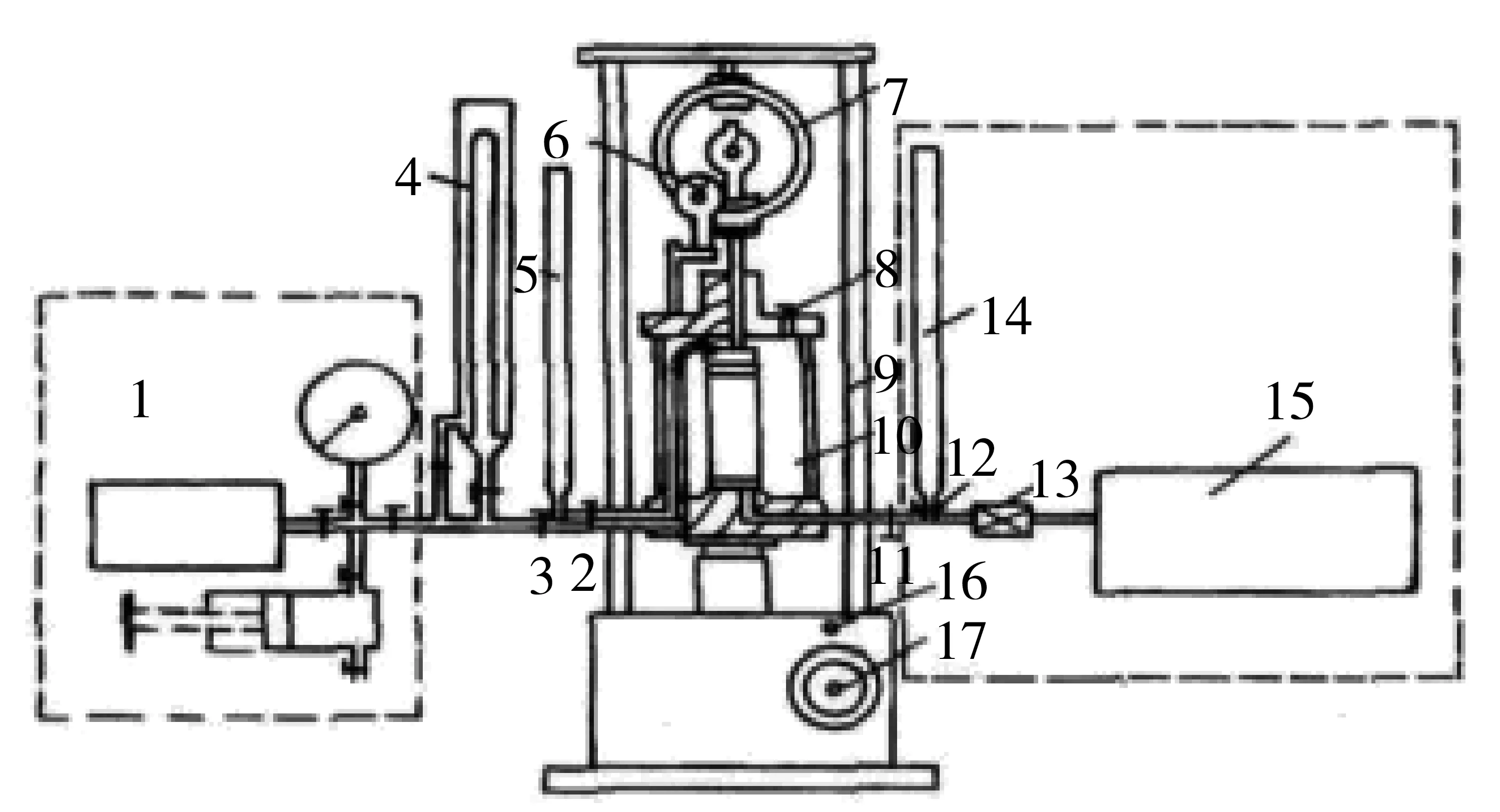
注:1-周围压力系统;2-周围压力阀;3-排水阀;4-体变管;5-排水管;6-轴向位移表;7-测力计;8-排气孔;9-轴向加压设备;10-压力室;11-孔压阀;12-量管阀;13-孔压传感器;14-量管;15-孔压测量系统;16-离合器;17-手轮。图1 TSZ-6A应变控制式三轴仪

TSZ-6A应变控制式三轴仪：南京土壤仪器厂有限公司，如图1所示；HG202-2(2A/2AD)电热干燥箱：南京盈鑫实验仪器有限公司；JSFD-粉碎机：上海嘉定粮油仪器有限公司。

2.3 试验方法

修正莱特-邓肯模型中的参数由轴向压缩和各向等压压缩试验确定。

2.3.1 轴向压缩试验

在TSZ-6A应变控制式三轴仪中，装好圆柱形样品，固定围压后启动电机对试样进行剪切，粮堆的变形有时间延迟，所以采用较慢的剪切应变速率：1.000 mm/min，记录轴向力与位移，并做出轴向力与位移关系曲线，稻谷压缩过程中测力计不会出现峰值，因此选取样品高度发生20%塑性形变时对应的轴向压力为最大主压力差[10]。在本试验中，选定5个围压：30、50、70、90、110 kPa，每1个围压试验重复3次。

2.3.2 等向压缩试验

在TSZ-6A应变控制式三轴仪中，装好圆柱形样品，对样品施加一定的压应力，此时σ1=σ2=σ3(即三主应力相等)。在本试验中，压力变化范围为：5～270 kPa；每步压力增量为5 kPa，记录稻谷的体积变化。试验重复3次。

2.4 弹性参数的确定

2.4.1 加卸载弹性模量Eur的确定

在轴向压缩试验确定了最大主压力差后，选取最大主应力差的1/10逐级加压和卸压,施加第1级压力，同时开动秒表，记录加压后1 min时位移计的读数，每隔1 min施加一级压力，测记位移计读数，施加到第4级压力为止；随后逐级卸压，每隔1 min卸去一级，并测记卸压后1 min时位移计的读数，直至施加的轴向压力全部卸去；重复加卸荷4遍后，继续加压直至破坏。然后按式(25)计算出粮堆的弹性模量。

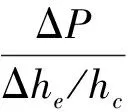
(25)

式中：Eur为粮堆的弹性模量/kPa；ΔP为轴向荷载/kPa；Δhe为粮堆的弹性变形量/mm；hc为试样固结后的高度/mm。

本试验测定并计算出的弹性模量Eur见表1。

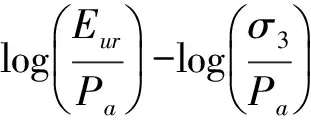
(26)

表1 不同含水率稻谷在不同围压下的弹性模量、体变模量和泊松比

不同含水率稻谷的log(Eur/Pa)-log(σ3/Pa)直线图见图2。

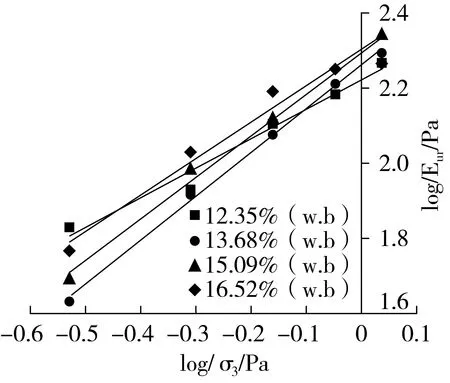
图2 不同含水率稻谷的弹性模量数K和弹性模量指数n

淮稻5号在含水率为12.35%、13.68%、15.09%、16.52% w.b.时拟合出的直线分别为y=0.796 4x+2.224 4、y=1.168 9x+2.262 4、y=1.103 1x+2.294、y=0.956 8x+2.300 3，由截距为log(K)，斜率为n，可知，弹性模量数K分别为167.65、182.98、196.79、199.66，随着含水率的增大而增大，弹性模量指数n分别为0.80、1.17、1.10、0.96，与含水率无关。

2.4.2 泊松比ν的确定

由等向压缩试验的卸载曲线可得到体变弹性模量,体变弹性模量按式(27)计算：

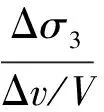
(27)

式中：Bur为稻谷堆的体变弹性模量/kPa。由试验数据计算得到的不同含水率稻谷在不同围压下的体变弹性模量见表1。

泊松比ν按公式计算：

ν=(3Bur-Eur)/6Bur

(28)

由式(28)计算的不同含水率稻谷在不同围压下泊松比见表1。可知，淮稻5号在含水率为12.35%、13.68%、15.09%、16.52% w.b.时的泊松比ν分别为0.204、0.214、0.221、0.268，随含水率的增大而减小；在同一含水率时，稻谷堆的泊松比随围压的增大而减小。

2.5 塑性塌落参数的确定

塑性塌落屈服时，式(5)、式(6)、式(7)整理为：

(29)

各向等压加载三轴试验，加载函数为：

(30)

塑性塌落功按式(31)计算：

(31)

(32)

不同含水率稻谷的log(Wc/Pa)-log(fc/Pa2)直线图见图3。

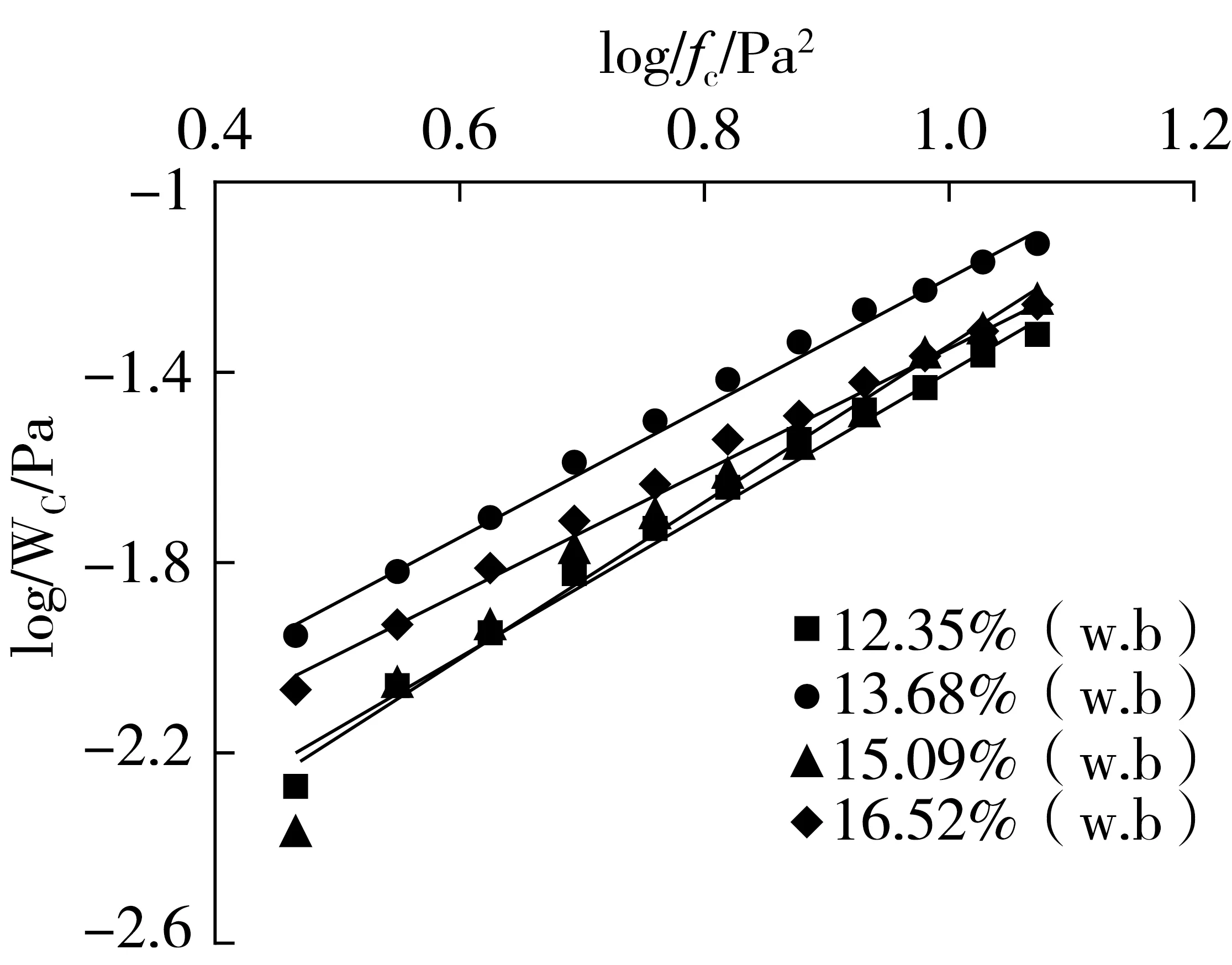
图3 不同含水率稻谷的塑性塌落模量C和塑性塌落指数p

淮稻5号在含水率为12.35%、13.68%、15.09%、16.52% w.b.时拟合出的直线分别为y=1.531 2x-2.922 9、y=1.374 8x-2.569、y=1.639 1x-2.984 6、y=1.304 4x-2.645 1，由直线截距为log(C)，斜率为p，可知，塑性塌落模量C分别为0.001 2、0.002 7、0.001 0、0.002 3，塑性塌落指数p分别为1.53、1.37、1.64、1.30，均与含水率无关。

2.6 塑性剪切参数的确定

2.6.1 破坏参数

粮堆破坏由fp控制，粮堆破坏时,

fp=η1

(33)

将式(13)代入式(33)有：

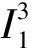
(34)

式(34)中，I1、I3是在轴向压缩试验破坏时计算得到的，不同含水率稻谷在不同围压下的最大破坏力及I1、I3见表2，做出log(I13-27)与log(Pa/I1)关系线性回归直线，由直线的斜率与截距可得到塑性剪切屈服常数η1与塑性剪切屈服指数m。线性回归直线方程为：

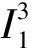
(35)

表2 不同含水率稻谷在不同围压下的最大破坏力及I1,I3

不同含水率稻谷的log(I13-27)与log(Pa/I1)关系线性回归直线见图4。

淮稻5号在含水率为12.35%、13.68%、15.09%、16.52%w.b.时拟合的直线分别为y=0.576 9x+2.348 9、y=0.932 3x+2.583、y=0.764 2x+2.317 2、y=1.138 8x+2.694 2，由此可知，塑性剪切屈服常数η1分别为223.31、382.82、207.59、494.54，塑性剪切屈服指数m分别为0.58、0.93、0.76、1.14，均与含水率无关。

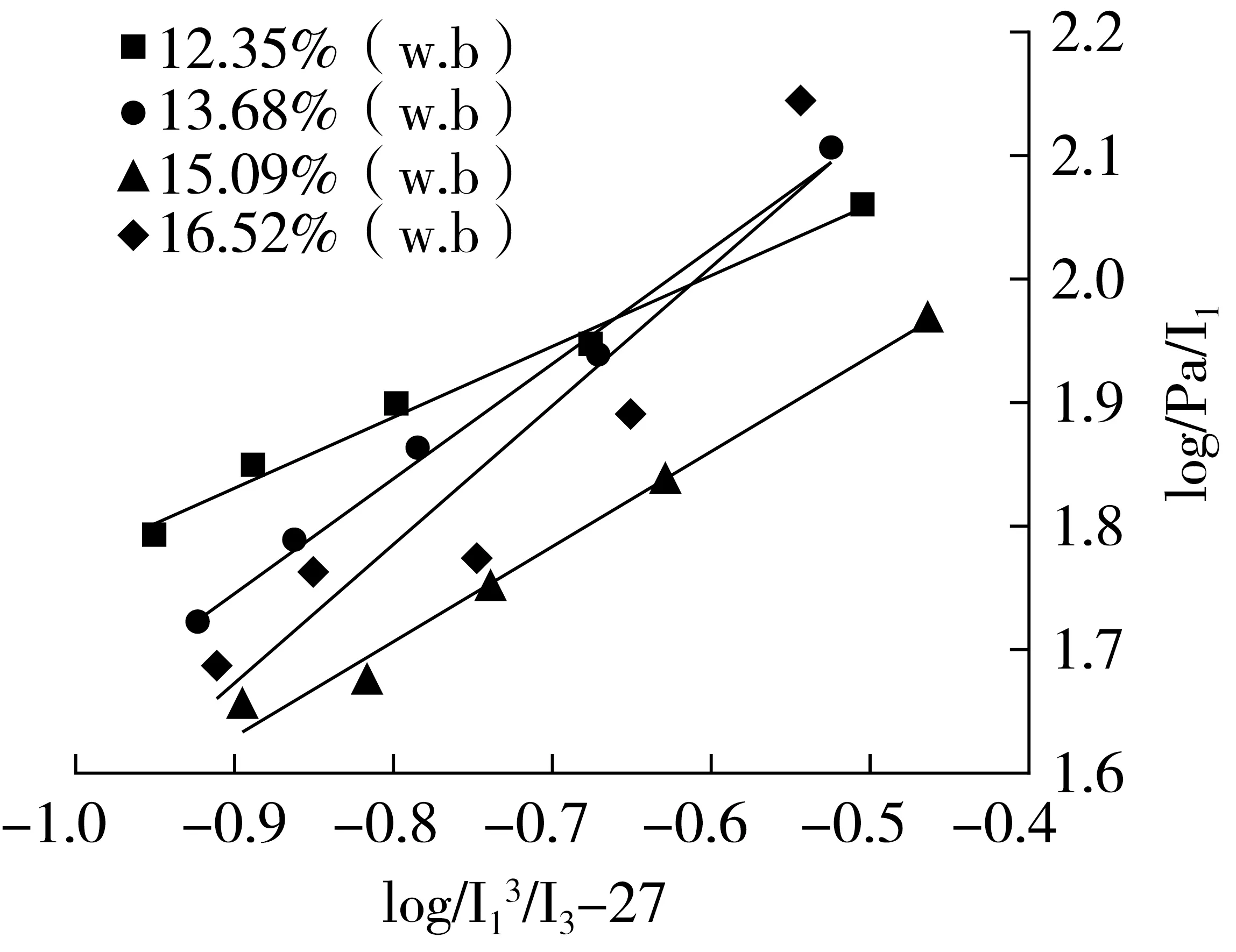
图4 不同含水率稻谷的塑性剪切屈服常数η1与塑性剪切屈服指数m

2.6.2 势参数

为了计算势参数S、R、t，将方程(22)分为2部分：

η2=S·fp+Y

(36)

(37)

式中：

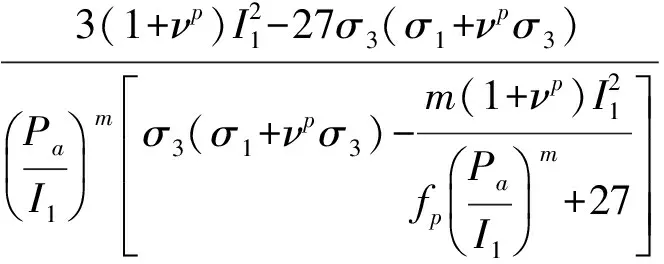
(38)

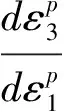
(39)

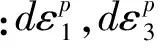
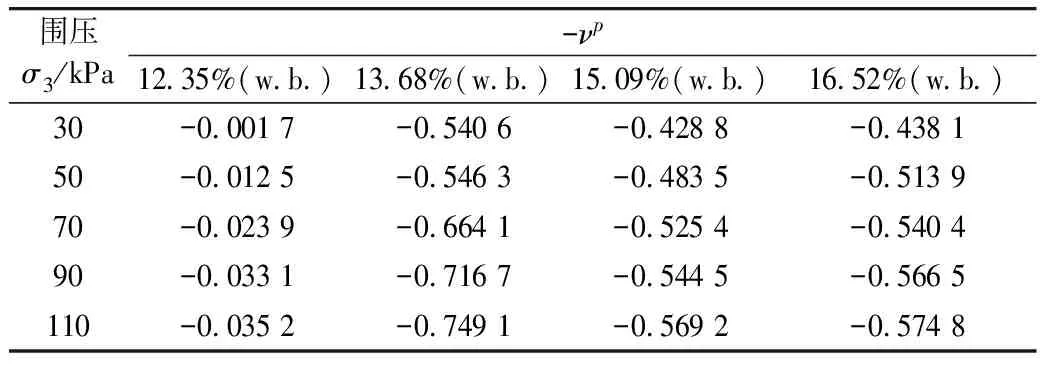
表3 不同含水率稻谷在不同围压下的-νp

计算这3个参数需要分2步，第1步,对于同一含水率不同围压σ3的稻谷,做出η2对fp的曲线图(淮稻5号含水率为12.35%(w.b.)，围压为30 kPa的η2-fp的曲线图见图5),每一个围压对应一个斜率S和一个截距Y,5个围压对应五组斜率S和截距Y。不同含水率不同围压下的S、Y值见表4。

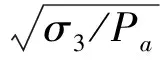
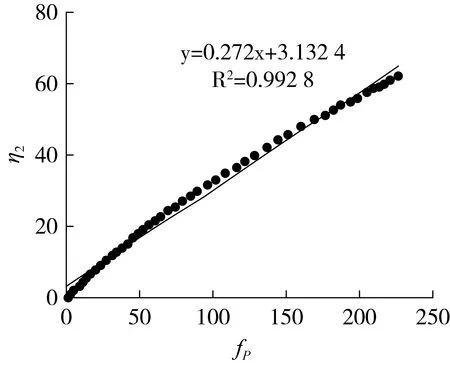
图5 含水率为12.35% w.b稻谷在30 kPa下的η2-fp曲线

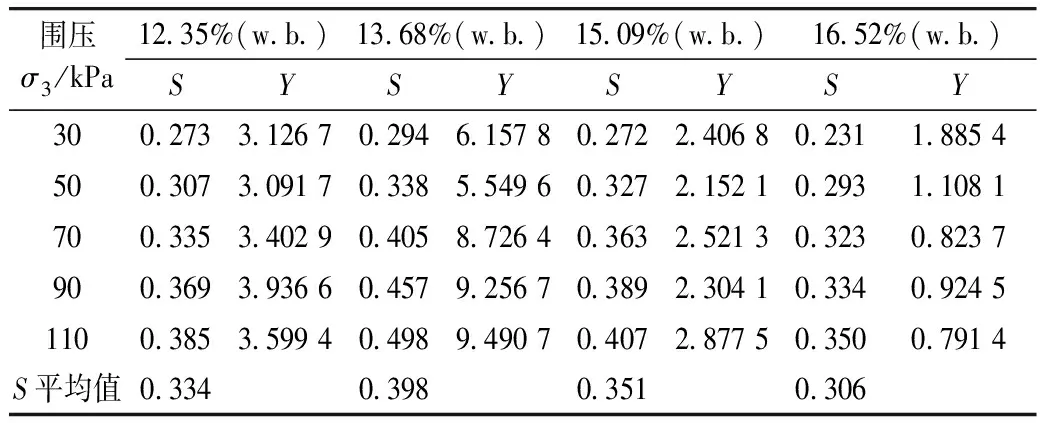
表4 不同含水率不同围压下稻谷的塑性剪切势参数S和Y

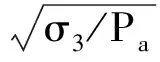
图6 不同含水率稻谷的Y-曲线图

淮稻5号在含水率为12.35%、13.68%、15.09%、16.52% w.b.时拟合的直线分别为y=1.446 7x+2.256 1、y=8.329 9x+1.068 8、y=0.810 5x+1.793 9、y=-2.015 7x+2.744 3，由此可知，塑性剪切势参数R分别为1.447、8.330、0.811、-2.016，t值分别为2.26、1.07、1.79、2.74，均与含水率无关。

2.6.3 功硬化参数

对于塑性剪切屈服条件，fp=Kp必须满足，有式(13)、式(14)即可得到：

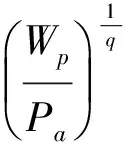
(40)

式中：a,b,q均为与σ3有关，见式(15)、(16)、(18)，另外，q值见如式(41)：

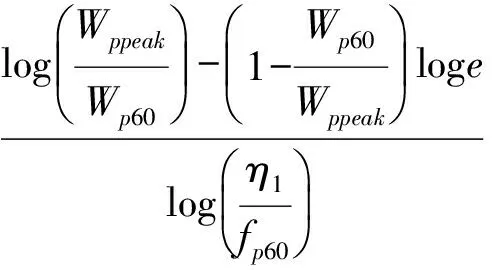
(41)

式中：(Wppeak,η1)为fp-Wp曲线的峰值点(淮稻5号水分1(12.35% w.b.)在30 kPa下的fp-Wp的曲线图见图7)，fp60=0.6η1，Wp60为与fp60相对应的剪切塑性功。依此计算，不同含水率不同围压下稻谷的Wppeak,η1，fp60，Wp60见表5。

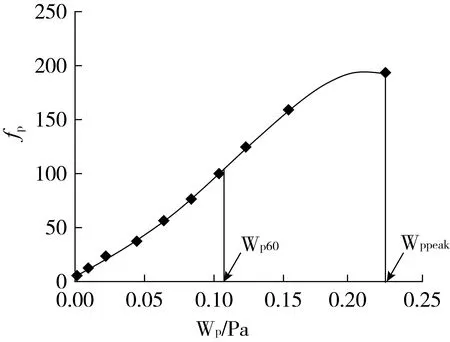
图7 水分1(12.35%(w.b.))稻谷在30 kPa下的fp-Wp曲线

表5 不同含水率不同围压下稻谷的Wppeak、η1、fp60、Wp60

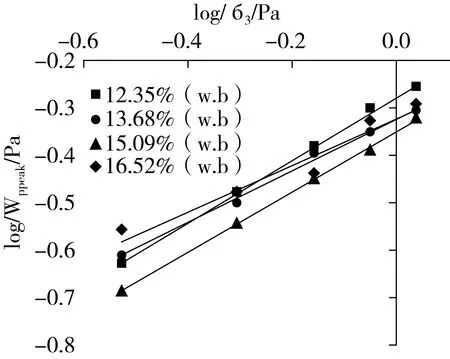
图8 不同含水率稻谷的硬化功参数θ和l

淮稻5号在含水率为12.35%、13.68%、15.09%、16.52% w.b.时拟合的直线分别为y=0.671 1x-0.273 2、y=0.546 8x-0.322 7、y=0.634 8x-0.349 4、y=0.488 4x-0.324 4，可知，硬化功参数θ分别为0.53、0.48、0.45、0.47，l分别为0.67、0.55、0.63、0.49，均与含水率无关。

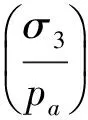
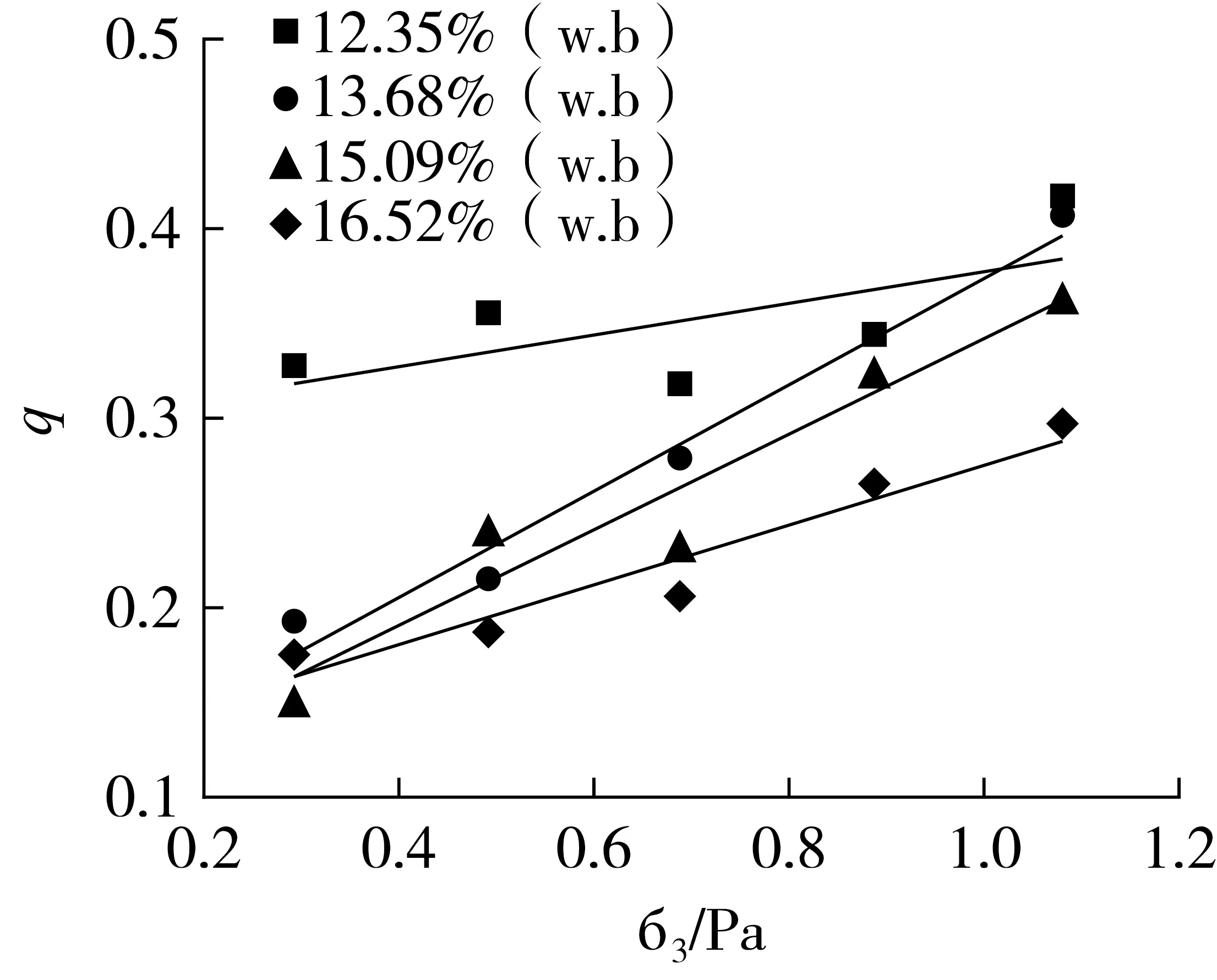
图9 不同含水率稻谷的硬化功参数α和β

淮稻5号在含水率为12.35%、13.68%、15.09%、16.52% w.b.时拟合的曲线分别为y=0.081 7x+0.295 5、y=0.279 7x+0.092 8、y=0.253 6x+0.087 2、y=0.158 5x+0.117，可知，硬化功参数α分别为0.30、0.09、0.09、0.12，β分别为0.08、0.28、0.25、0.16，均与含水率无关。

3 结论

3.1 修正莱特-邓肯模型特别适用于描述塑性变形大的稻谷堆的应力应变行为。在该模型中，稻谷堆的模型参数均可以通过三轴压缩试验数据来确定，所确定的参数是应用修正莱特-邓肯模型计算稻谷堆在筒仓中的应力、应变、密度、孔隙率分布的必要参数。该参数的计算，对修正莱特-邓肯模型的使用，以及研究筒仓中稻谷堆的密度分布、孔隙率分布、粮堆变形程度、总重量计算、对仓壁的侧压力以及粮仓的设计具有重要意义。

3.2 各不同含水率稻谷的修正莱特-邓肯模型参数见表6。

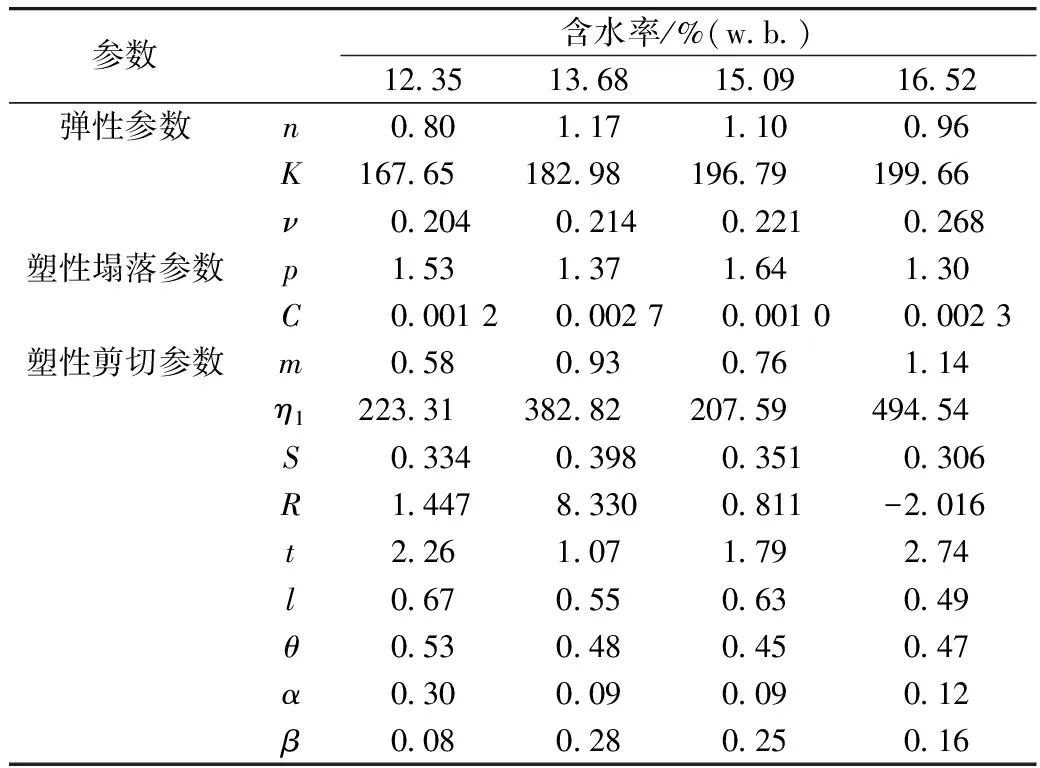
表6 不同含水率稻谷的修正莱特-邓肯模型参数

3.3 所有的弹塑性参数中只有K、ν随含水率的增大而增大，其它参数均与含水率无显著性关系。

[1]Jofriet J C,Lievre B L,Fwa T F.Friction model for finite element analyses of silos[J].Trans of the ASAE,1977,20:735-740

[2]Bishara A G.Static pressure in concrete circular silos storing granular materials[J].ACI Jnl,1983,55-62

[3]Ooi,Botter.Wall pressure in squat steel silos from simple finite element analysis[J].Computers& Structures,1990,37(4):361-374

[4]曾丁,黄文彬,华云龙.筒仓壁压的有限元分析[J].农业工程学报,1998,14(2):44-48

Zeng D,Huang W B,Hua Y L.Finite element analysis of silo wall pressure[J].Transactions of the CSAE,1998,14(2):44-48

[5]李兴照,王录民,黄茂松.大直径粮食浅圆仓仓壁压力有限元分析及验证[J].特种结构.2005,22(1):97-99

Li X Z,Wang L M,Huang M S.Finite element analysis and verification of the wall pressure of large diameter grain silo[J],Special Strucyures,2005,22(1):97-99

[6]陆新征,陈勇.某特大型筒仓侧壁压力有限元分析[J],山西建筑,2006,32(2)：1-2

Lu X Z,Chen Y.Finite element analysis of wall pressure in a large silo[J].Shanxi Architecture,2006,32(2)：1-2

[7]张炎圣,杨晓蒙,陆新征.钢板筒仓侧壁压力的非线性有限元分析[J].工业建筑,2008,38：447-451

Zhang Y S,Yang X M,Lu X Z.Nonlinera finite element analysis of the wallpressure in a steel silo[J].Industrial Construction,2008,38：447-451

[8]安蓉蓉.粮食的内摩擦角、弹性模量及体变模量的实验研究[D].南京：南京财经大学,2010：28-32

An R R.Experiment study of angle of internal friction,elastic modulus and bulk strain modulus of grain[D].Nanjing：Nanjing University of Finance and Economics,2010：28-32

[9]程绪铎,石翠霞，陆琳琳，等.小麦粮堆体变模量的实验测定与研究[J].粮食储藏,2010,39(5)：13-16

Cheng X D,Shi C X,Lu L L,et al.Measurement and experiment on bulk strain modulus of wheat[J].Grain Storage,2010,39(5)：13-16

[10]陆琳琳,石翠霞,程绪铎.稻谷堆弹性模量的实验测定与研究[J].粮食储藏,2011,40(3)：31-35

Lu L L,Shi C X,Cheng X D.Determination and research on elastic modulus of paddy pile[J].Grain Storage,2011,40(3)：31-35

[11]石翠霞,陆琳琳,程绪铎.小麦粮压缩特性的实验研究[J].粮食储藏,2011,40(4)：33-37

Shi C X,Lu L L,Cheng X D.Exprerimental research on compressuion properties of wheat pile[J].Grain Storage,2011,40(4):33-37

[12]Zhang Q.Determination of elastoplastic constitutive parameters for wheat en masse[J].Trans of the ASAE,1986,29(6):1739-1746

[13]Zhang Q.Static and thermal loads in full size grain bins predicted by vectorized FEM on supercomputer[J].Trans of the ASAE,1989,32(2):685-691

[14]陈晓平,杨光华,杨雪强.土的本构关系[M].北京：中国水利水电出版社,2011：93-103

Chen X P,Yang G H,Yang X H.Soil constitutive models[M].Beijing：China Water & Power Press,2011：93-103.

Parameters of Modified Lade-Duncan Model for Grain

Du Xiaocui Cheng Xuduo Gao Mengyao Feng Jiachang
(College of Food Science and Engineering/Collaborative Innovation Center for Modern Grain Circulation and Safety,Nanjing University of Finance and Economics,Nanjing 210046)

A constitutive stress-strain equation,formulated from Modified Lade-Duncan Model,can be used to model behavior of grain.In this paper,the 14 parameters of the theory were calculated by using TSZ-6A type of controlled triaxial apparatus on four different moisture content of grain heap in axial compression test and the isotropic compression test.The test results show that the elastic parameterKof the moisture content of 12.35%,13.68%,15.09%,16.52%(w.b.)of paddy were 167.65，182.98，196.79，199.66，nwere 0.80，1.17，1.10，0.96，νwere 0.204、0.214、0.221、0.268；the plastic collapse parameterCwere 0.001 2，0.002 7，0.001 0，0.002 3,pwere 1.53，1.37，1.64，1.30 respectively;plastic expansive parameterη1were 223.31，382.82，207.59，494.54,mwere 0.58，0.93，0.76，1.14,Swere 0.334，0.398，0.35，0.306,Rwere 1.447，8.330，0.811，-2.016，twere 2.26，1.07，1.79，2.74，θwere 0.53，0.48，0.45，0.47，lwere 0.67，0.55，0.63，0.49，αwere 0.30，0.09，0.09，0.12，βwere 0.08，0.28，0.25，0.16 respectively.And theKandνincrease with the water content,νwith the confining pressure decreases,there was no significant relationship between moisture and other parameters.

grain，Modified Lade-Duncan Model，model parameter

TS210.4

A

1003-0174(2017)09-0131-08

国家自然科学基金(31371856)，江苏高校优势学科建设工程(苏政办(2014)37号)

2016-07-04

杜小翠，女，1991年出生，硕士，食品科学工程

程绪铎，男，1957年出生，教授，粮食储藏工程