关于一类双单叶函数的系数估计
敖 恩,汤 获,杨静宇
(1.赤峰学院 数学与统计学院;2.赤峰学院 应用数学研究所,内蒙古 赤峰 024000)
关于一类双单叶函数的系数估计
敖 恩,汤 获,杨静宇
(1.赤峰学院 数学与统计学院;2.赤峰学院 应用数学研究所,内蒙古 赤峰 024000)
在本文中,引进一类由拟从属关系定义的双单叶函数新子类,结合正实部解析函数的系数估计和分析技巧,研究函数类的起始项a2和a3的边界估计问题及Fekete-SzegÖ问题,得到准确结果,并推广及改进一些已有的结论.
解析函数;双单叶函数;系数估计
1 引言
用A表示所有在单位圆盘U={z∈C:|z|<1}内解析且具有形式

的函数族.记S表示A内在单位圆盘U={z∈C:|z|<1}内单叶解析函数的全体.
著名的Koebe one-quarter Theorem[1]表明每一个函数都存在一个逆函数f-1,满足

和

若一个函数f∈A在U内称为是双单叶的当且仅当f和f-1在U内都是单叶的.用σ表示在单位圆盘U内双单叶的函数的全体.若则

1970年,在文献[2]中,Robertson引入了拟从属的概念.设函数f(z)和h(z)在单位圆盘U内解析,若存在一个解析函数φ(z),使得在U内解析且

满足

则称函数f(z)在U内拟从属于h(z),记为f(z)≺qh(z).特别地,当φ(z)=1 时,f(z)=h(ω(z)),z∈U,此时称函数 f(z)在 U 内从属于函数 h(z),记为 f(z)≺h(z);
当 ω(z)=z时,f(z)=φ(z)h(ω(z)),z∈U,此时称函数 f(z)在 U内优于函数h(z),记为f(z)≪h(z).因此从属关系和优化关系是拟从属关系的两种特殊情形.
在文献[3]中,Lewin首先引入双单叶函数族σ,并对系数进行估计,得到了若 f∈σ,则 |a2|≤1.51.在文献[4]中,Branan 和Clunie推测若 f∈σ,则在文献[5]中,Netanyahuz 证明了若 f∈σ,则由此开始,许多学者开始引入与双单叶函数族相关的一些重要子类,并研究其系数估计问题[6-11].
1976年,在文献[12]中,Noonan和Thomas研究了函数f∈A系数的q阶Hankel多项式Hq(n)(q≥1,n≥1)如下:

特别地,H2(1)=|a3-a22|为Fekete-SzegÖ问题的特殊情况.近来许多学者也对于Hankel多项式产生了极大的兴趣 (如[13],[14]).受以上工作的启发,本文利用拟从属关系引入一类双单叶函数类,定义如下:

则称 f(z)∈Nq,σ(γ,λ,δ;ø),其中 γ∈C{0},λ≥1,δ≥0,g(ω)=f-1(ω).
当参数取特殊值时,可得到一些特殊的函数子类,例如:
(1)Nq,σ(1,λ,0;ø)=(λ,ø)(见文献[12]);
q,σ
(3)Nq,σ(γ,1,0;ø)=(ø)满足

(4)Nq,σ(γ,1,1;ø)=(ø)满足

在本文中,利用正实部解析函数的系数估计和分析技巧,研究了函数类 Nq,σ(γ,λ,δ;ø)中函数起始项 a2和 a3的边界估计问题及Fekete-SzegÖ问题的特殊情况.
为了得到本文的主要结果,需要引进下面的引理.
引理[15]设则 |pk|≤2,k=1,2,…,其中P表示正实部函数族,即P表示在单叶圆盘U内解析且满足p(0)=1,Re{p(z)}>0 的函数的全体.
2 主要结果
为了得到本文的主要结果,在U内定义函数p1(z),p2(ω)为

则函数 p1(z),p2(ω)在 U 内解析,且 p1(0)=p2(0)=1.于是

由解析函数u,v:U→U可得到函数p1(z),p2(ω)有正实部,则 |pi|≤2,|qi|≤2.
除特别声明,本文规定

定理 1 设 f(z)∈Nq,σ(γ,λ,δ;ø),则

和

证明 设 f(z)∈Nq,σ(γ,λ,δ;ø),则根据定义存在解析函数 u,v:U→U 满足
及解析函数 ψ(z),φ(z)满足 |ψ(z)|<1,|φ(z)|<1使得
将 f(z)=z+a2z2+a3z3+…和 g(ω)=ω+b2ω2+b3ω3+…分别代入(2.8)式和(2.9)式左侧,通过简单计算可得


又将(2.1),(2.3)和(2.5)代人(2.8)式右侧, 整理可得

同理将(2.2),(2.4)和(2.5)代人(2.9)式右侧,整理可得

于是将(2.10)和(2.12)代入到(2.8)式,比较两边同次幂的系数可得

由于 b2=-a2,b3=2a22-a3,则将(2.11)和(2.13)代入到(2.9)式,比较两边同次幂的系数可得

由(2.14)和(2.16)得

由(2.15)和(2.17)得

在(2.18)和(2.19)中利用引理,便可得出(2.4)式中给出的|a2|的上界.
下面再讨论 |a3|的上界.由(2.15)和(2.17)得

将(2.18)代入到(2.20)式,有
由引理可得
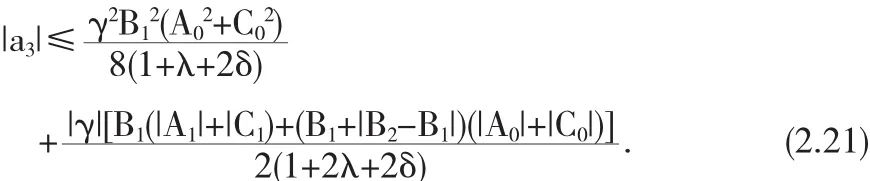
另一方面,将(2.19)代入到(2.20)式,有


结合(2.21)和(2.22)式,即可得(2.7)式成立.因此,定理 1 证毕.
在定理1中,分别令γ=1,δ=0和λ=1,得到下面两个推论:
推论 1 设



推论 2 设
和

注明 推论1和推论2改进了文献[16]和[17]中的相应结果.
在推论2中,分别令δ=0和δ=1,得到下面两个推论:

和


和

另外,在(2.20)式中利用引理可以得到下面定理2.定理2中结果是Fekete-SzegÖ问题的一个特殊情况,即二阶Hankel多项式H2(1)=|a3-a22|的上界估计.
定理 2 设 f(z)∈Nq,σ(γ,λ,δ;ø),则

〔1〕Duren P L.UnivalentFunctions[M].New York:Springer-Verlag,1983.
〔2〕M.S.Robertson.Quasi-subordination and coefficient conjectures[J].Bulletin of the American Mathematical Society.1970,76:1-9.
〔3〕Lewin M.On a coefficient problem for bi-univalent functions[J].Proc Amer Math Soc,1967,18:63–68.
〔4〕Brannan D A,Clunie J G.Aspects of Contemporary Complex Analysis(Proceedings of the NATO Ad-vanced Study Instute Held at the University of Durham,Durham:July 1-20,1979).New York:Academic Press,1980.
〔5〕Netanyahu E.The minimaldistance ofthe image boundary from the origin and the second coefficient of a univalent function in|z|<1[J].Arch Rational Mech Anal,1969,32:100–112.
〔6〕Srivastava H M,Mishra A K,Gochhayat P.Certain subclasses of analytic and bi-univalent functions[J].Appl Math Lett,2010,23:1188–1192.
〔7〕Frasin B A.,Aouf M K.New subclasses of bi-univalent functions[J].Appl Math Lett,2011,24:1569–1573.
〔8〕Xu Q H,Xiao H G,Srivastava H M.A certain general subclass of analytic and bi-univalent functions and associated coefficientestimateproblems[J].ApplMath Comput,2012,218(23):1461-1465.
〔9〕Srivastava H M.,Bulut S,Caglar M,et al.Cofficient estimats for a general subclass of analytic and bi-univalent functions[J].Filomat,2013,27(5):831-842.
〔10〕Peng Z G,Han Q Q.On the coefficients of several classes of bi-univalent funcions.Acta Math.Scientia,2014,34B(1):228–240.
〔11〕石磊,王智刚.两类双单叶非Bazilevic函数族的系数估计[J].安徽大学学报,2016,40(3):17-21.
〔12〕Noonan J W,Thomas D K.On the second Hankel determinantofareally mean p-valentfunctions[J].Trans.Amer.Math.Soc..1976,223:337-346.
〔13〕ArifM,NoorK I,RazaM.Hankeldeterminant problem of a subclass of analytic functions[J].J.Inequal.Appl.2012,22.
〔14〕Babalola K O.On Hankel determinant for some classes of univalent functions[J].Inequality Theorey and Applications.2007,6:1-7.
〔15〕C.Pommerenke,Univalent Functions[M],Vandenhoeck&Ruprecht,G¨ottingen,1975.
〔16〕Amol B.Patil,Uday H.Naik.Estimates on Initial Coefficients of Certain Subclasses of Bi-Univalent Functions Associated with Quasi-Subordination[J].Global Journal of Mathematical Analysis,2017,5(1):6-10.
〔17〕S.P.Goyal,Onkar Singh and Rohit Mukherjee.Certain results on a subclass of analytic and bi-univalent functions associate with coefficient estimates and quasisubordination[J].Palestine Journal of Mathematics.Vol.5(1)(2016),79–85.
O174.51
A
1673-260X(2017)10-013-03
2017-08-03
国家自然科学基金(11561001);内蒙古自然科学基金项目(2014MS0101);内蒙古高等学校科学研究项目(2015NJZY240)

