半主动浮筏隔振系统的模糊PID控制
赵 成
(苏州市职业大学 自动化系,江苏 苏州 215104)
半主动浮筏隔振系统的模糊PID控制
赵 成
(苏州市职业大学 自动化系,江苏 苏州 215104)
对带有电流变液智能阻尼器的半主动双层浮筏隔振系统设计了一种模糊PID控制器。将半主动浮筏隔振系统中间质量的位移及其导数作为模糊控制器的输入,PID控制器的三个增益参数作为其输出,利用电流变液智能阻尼器的阻尼力可随电压变化的特性来降低中间质量的振动。仿真分析了多种激励下浮筏隔振系统的输出力响应。仿真结果表明:与最优被动阻尼和电流变液阻尼器最大阻尼系统相比,模糊PID控制下的半主动浮筏隔振系统的减振效果最好。
半主动;浮筏;模糊PID
0 引 言
浮筏是应用于船舰上的一种新型隔振降噪装置,它是把船舰中的马达、风机等多台动力设备弹性地安装在一个公共的筏架上,再将筏架弹性地安装在船身基础上。实际上,浮筏就是一种特殊的双层隔振系统,其机理是利用浮筏装置中弹性元件的阻尼和中间质量的设计来控制并衰减振动能量,使船舰表壳的振动减小。
从六十年代起,国内外许多学者在船舰的减振降噪方面进行了大量研究,提出了许多种方法并发表了相关论文[1-4]。近三十多年来,越来越多从事船舰设计的专家认为,船舰的减振降噪是一个急需解决的重要问题。降低舱室的振动和噪声不仅可以改善船舰上人员的居住和工作环境,重要的是能够保障船舰上精密仪器设备的正常运行,保证船舰的正常行使,特别是对于军用舰艇来说,能够增加其航行的稳定性和隐蔽性,提高战斗力。因此,改善船舰上浮筏隔振系统的减振性能是一个十分重要的问题。
PID控制算法简单、稳态性能好,但动态性能差;而模糊控制,作为一种语言型智能控制,方法简单灵活,采用手动控制规则或由专家经验建立的模糊控制规则,模拟人脑的逻辑推理和决策过程,可以处理系统的非线性和不确定性问题,且不依赖于受控对象的模型,动态性能好。对于本文研究的双层浮筏隔振系统,电流变阻尼器存在强非线性特性,由此本文将模糊控制方法与PID控制方法相结合来控制半主动浮筏隔振系统[5-6],将半主动浮筏隔振系统中间质量的位移及其导数作为模糊控制器的输入,PID控制器的三个增益参数作为其输出。然后由PID控制器求出所应施加的可控力并生成相应的电压加到电流变智能阻尼器上,完成控制作用,达到期望的减振效果。
1 带有电流变智能阻尼器的浮筏隔振系统模型
1.1 浮筏隔振系统模型
图1为基于电流变智能阻尼器的双层浮筏隔振系统模型。其中:m1、m2分别为上层质量、中间质量;k1、k2为弹簧刚度;c0为零电场粘性阻尼系数;u为可控屈服阻尼力;z1、z2为位移;fin为竖直方向的激振力;fout=k2z2为基座受到的振动力;力传递率为:T=fout/fin。
浮筏系统动力学方程为:
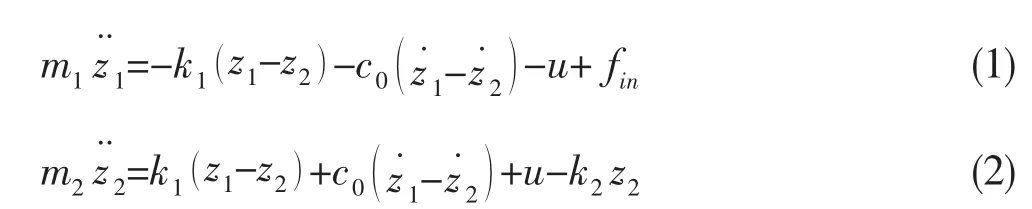
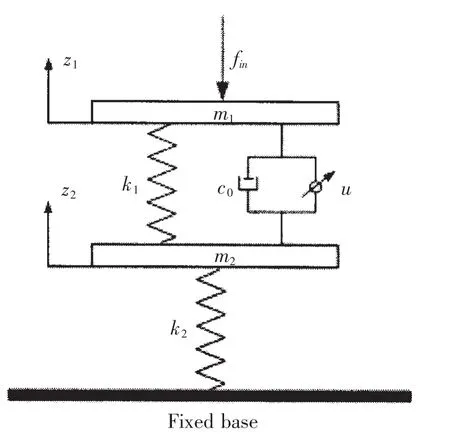
图1 双层浮筏隔振系统模型Fig.1 The model of two-stage floating raft isolation system
1.2 浮筏隔振台架
本文设计了如图2所示的力隔振台架。
力隔振台架由激振器A1、上层板A5、初级隔振弹簧A6、中层板A7和次级隔振弹簧A8构成,并通过4个限位杆A3竖直地安装在基础之上,如图2所示。
力隔振台架上安装了多种传感器,可以测量各种物理量。
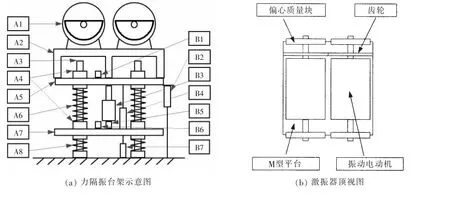

图2 力隔振台架Fig.2 Diagram of force isolation
1.3 激振力分析
如图3中所示,m0为单个偏心质量块的质量。假设变频器控制电动机做匀速转动,角速度为ω。由图3可知,在t时刻,m0与m1竖直方向的相对速度关系为:

经过Δt之后,m0与m1的相对速度如下:
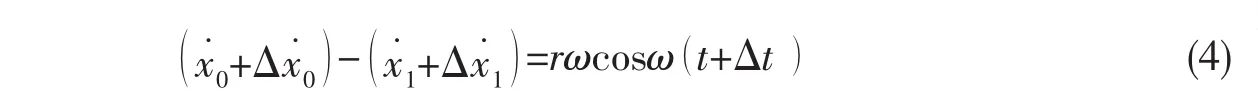
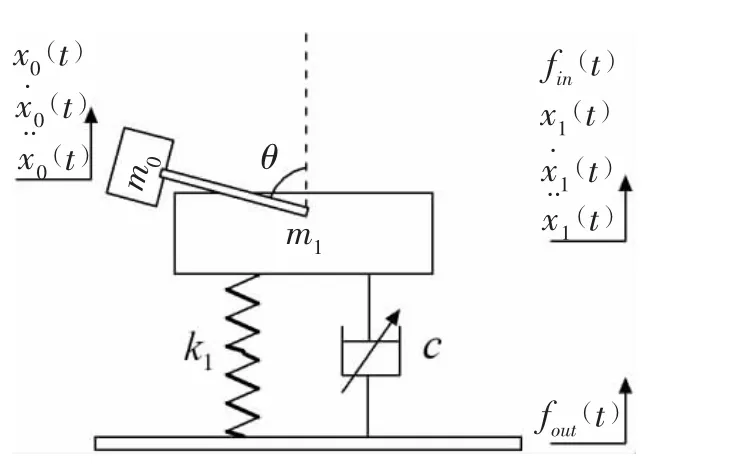
图3 力隔振台架激振力模型Fig.3 Mechanical model of exciting force
而

把(3)、(5)、(6)式代入(4)式,有
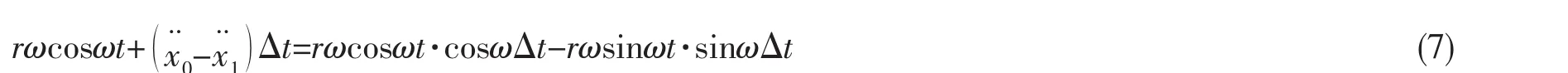
当 Δt→0 时,cosωΔt→1,sinωΔt→ωΔt,于是(7)式可化简为:

忽略偏振质量块的重量影响,由牛顿第三运动定律,m1在竖直方向所受到的激振力如下:

1.4 电流变阻尼器模型
由实验数据,拟合出u与电压U的关系式:

经试验确定的常数为:c0=1 013.4 N s/m,a0=10.23 N,a1=6.38 N·kV,a2=2.59 N·kV2。
图4为不同电压作用下阻尼力-活塞速度关系曲线。由图可见,仿真与试验结果非常接近,表明阻尼器力学模型是合理的。
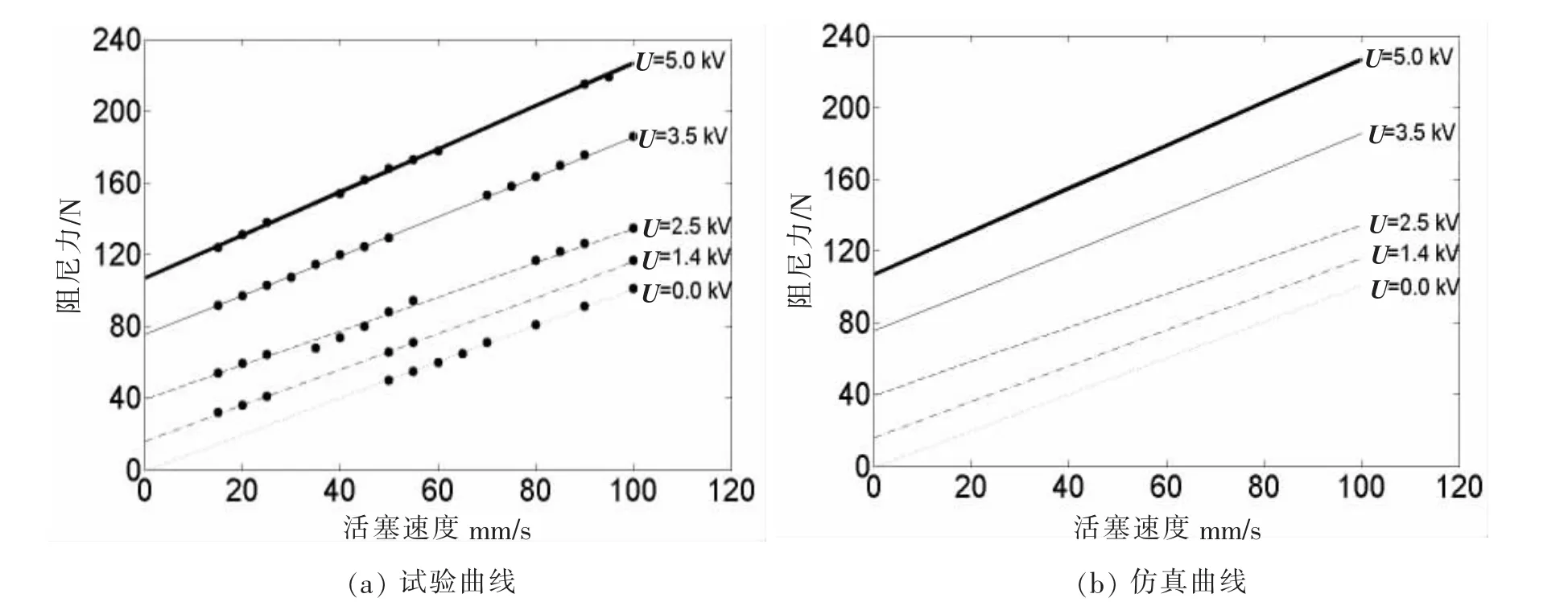
图4 不同电压作用下阻尼力-活塞速度关系曲线Fig.4 Damping force versus piston velocity at various voltages
2 半主动模糊PID控制器设计
图5显示了模糊PID控制系统的工作原理。当有外界激励输入时,中间质量将会偏离平衡位置0而上下摆动,利用位移传感器测量中间质量的绝对位移z2,此时的偏差记作e=0-z2,将此偏差e及偏差的导数e˙按照大小和方向分类,然后针对不同的分类情况根据人们的经验知识给出不同的PID参数并将其输出给PID控制器得到所应施加的可控阻尼力,最后根据高压发生器给出相应的电压加到电流变阻尼器上,完成控制过程。
2.1 PID 初始参数的设置
PID控制就是将系统偏差的比例—积分—微分进行线性组合构成的控制作用,其控制算法为:

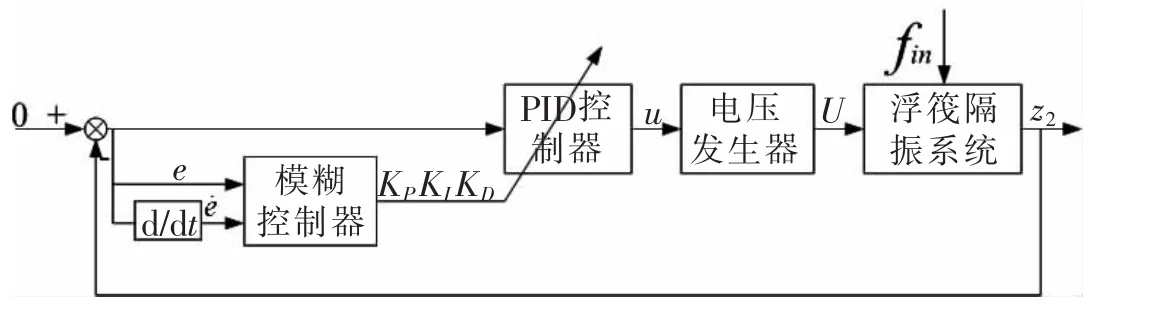
图5 模糊PID控制策略框图Fig.5 Fuzzy-PID control block diagram of semi-active floating raft isolation system
(11)式中:u(t)为PID控制器的输出信号;e(t)为偏差信号;KP为比例增益;TI=KP/KI为积分时间常数;TD=KD/KP为微分时间常数;KI为积分增益;KD为微分增益。
PID控制器的初始参数KP0、KI0和KD0用齐格勒—尼柯尔斯规则来确定。
在(11)式中,设TI=∞、TD=0,即此时的控制器仅为比例控制作用。将比例增益KP由0逐渐增加至临界值KL,此时系统的单位阶跃响应曲线第一次出现固定的等幅振荡。记录出此时的比例增益KL和相应的振荡周期TL,然后可根据如下关系式得出PID控制器的各个初始参数,

由(12)式得出的参数再根据实际系统进一步的微调,即可得到较好的PID控制器的初始参数KP0、KI0和KD0。
2.2 模糊控制器设计
将中间质量的位移偏差e及偏差的导数e˙和输出PID参数KP、KI和KD的物理论域量化到整数论域 {-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6}中,在其论域上均设有7个档次的语言变量值,它们为:负大(NB),负中(NM),负小(NS),零(ZE),正小(PS),正中(PM),正大(PB)。 其量化因子分别为 Ke、Ke˙、Kup、Kui和 Kud。 可以根据偏差e及偏差的导数e˙的实际大小来调整各个量化因子的大小。
输入、输出变量的隶属函数均选为高斯型隶属函数,均如图6所示。
根据中间质量的位移偏差e及偏差的导数
e˙的大小和方向的不同,可以对PID参数进行不同的调节。模糊控制规则表如表1~3所示。
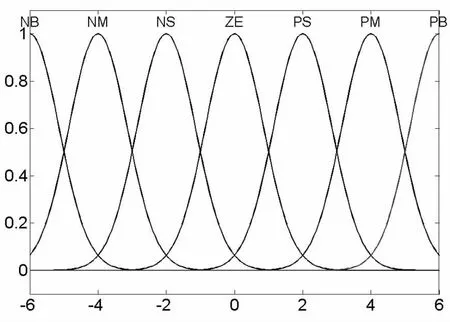
图6 模糊语言变量的隶属度函数Fig.6 Membership function of input and output linguistic variables
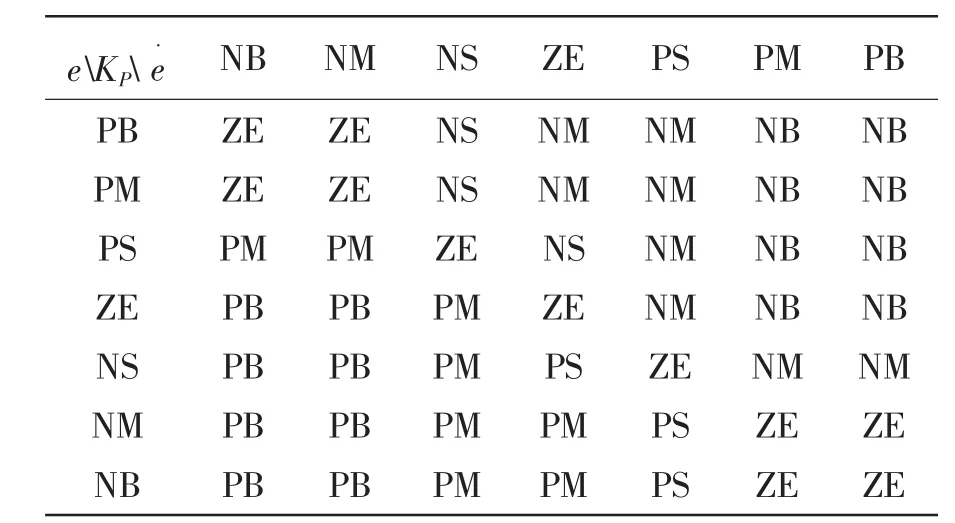
表1 KP模糊规则Tab.1 Fuzzy rules of KP
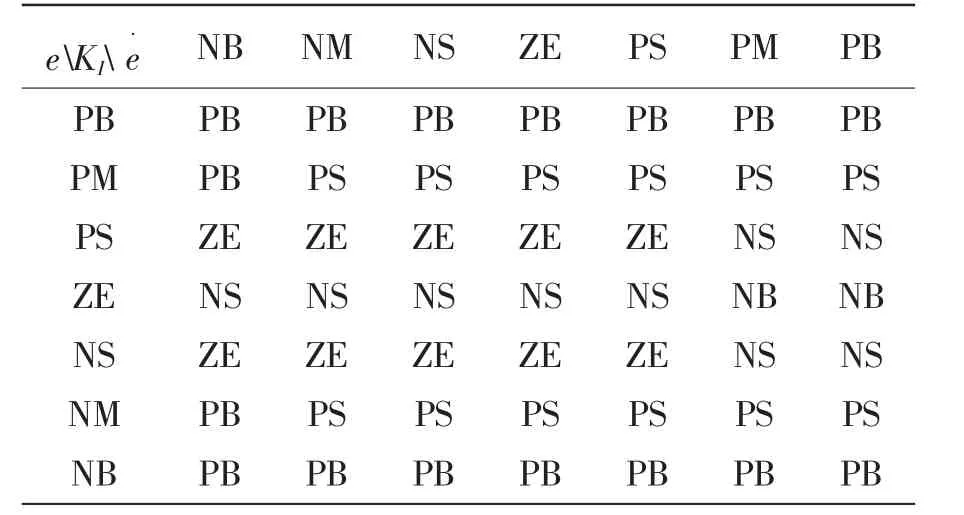
表2 KI模糊规则Tab.2 Fuzzy rules of KI
采用加权平均法对输出变量进行解模糊化,然后乘以相应的量化因子Kup、Kui及Kud就可得到PID控制器的参数 KP、KI和 KD。
2.3 半主动约束条件
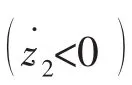
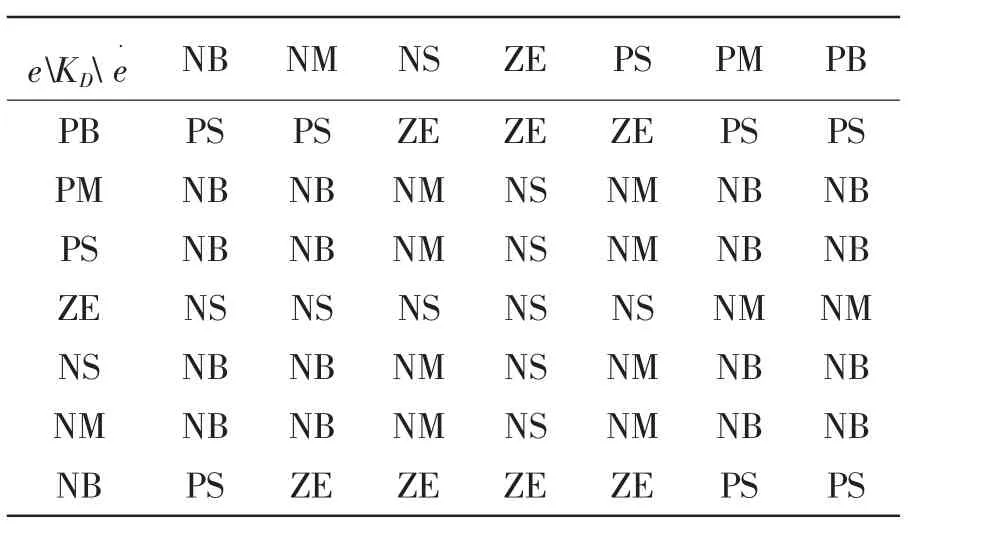
表3 KD模糊规则Tab.3 Fuzzy rules of KD

在确定了可控阻尼力后,由(10)式就得到施加在电流变阻尼器上的电压:

3 仿真实验
运用Matlab/Simulink对系统进行仿真,仿真参数为:
m0=3.2 kg,m1=32 kg,m2=8 kg,r=0.002 m,k1=33 000 N/m,k2=120 000 N/m,copt=1 685.3 N s/m,c0=1 013.4 N s/m,Umax=5 kV,a0=10.23 N,a1=6.38 N·kV,a2=2.59 N·kV2,cmax=2 055 N s/m。其中:copt为最优被动阻尼,cmax为电流变液阻尼器最大阻尼。
3.1 扫频激励输入
输入为幅值为100 N、频率为0~30 Hz的扫频激励力,扫频时间为30 s。
图7为单个正弦扫频激励下浮筏隔振系统的输出力响应曲线。从图7中可以看出,与最优被动阻尼和电流变液阻尼器最大阻尼隔振系统相比,半主动模糊PID控制下的双层浮筏隔振系统的减振效果最好,使基座受力得到有效的降低,提高了船舰行使的安全性。
3.2 一阶共振频率正弦激励
输入幅值为200 N、频率为一阶共振频率5 Hz的正弦激励力。
图8为一阶共振频率正弦激励下浮筏隔振系统的输出力响应。图8说明了半主动模糊PID控制下的双层浮筏隔振系统能有效地抑制一阶共振。
3.3 半波正弦激励
输入为半波正弦激励力,表达式如下:
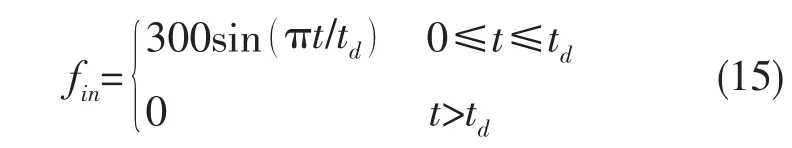
冲击持续时间td=0.1 s。
图9为半波正弦激励下浮筏隔振系统的输出力响应。从图9可以看出,最优被动阻尼隔振系统与最大阻尼隔振系统在冲击的最高峰的响应明显要高于半主动模糊PID控制下的双层浮筏隔振系统的响应,在冲击激励过后,半主动模糊PID控制作用下浮筏隔振系统的输出力瞬态响应衰减最快。
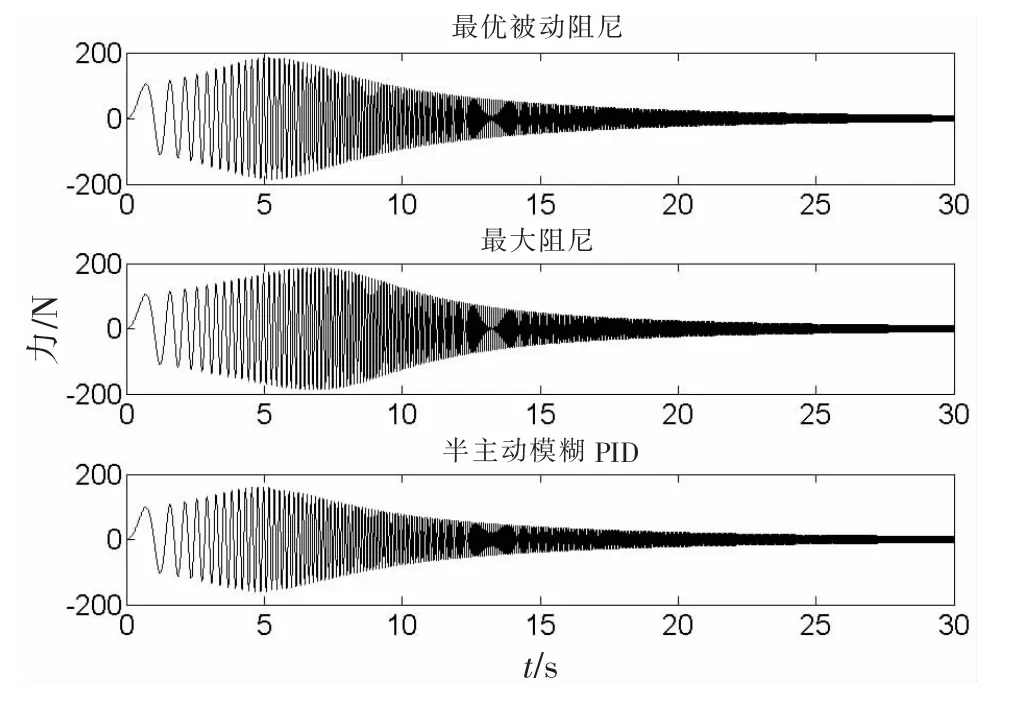
图7 扫频激励下浮筏隔振系统的输出力响应曲线Fig.7 Output force response of floating raft isolation system to one chirp signal
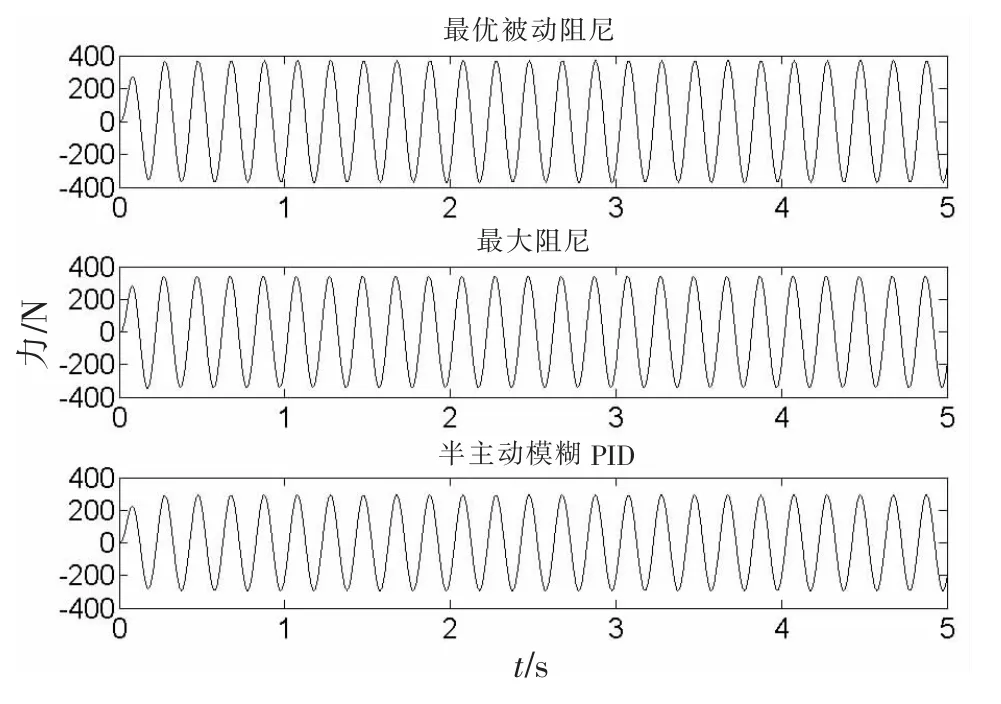
图8 一阶共振频率正弦激励下浮筏隔振系统的输出力响应曲线Fig.8 Output force response of floating raft isolation system to harmonic excitation
3.4 双频信号激励
激励信号由两个单频信号合成得到,信号的形式为:
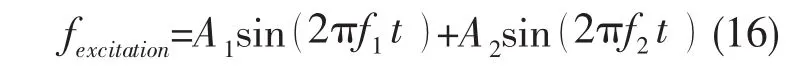
上式中fexcitation是激励信号而不是激励力。本文研究的双层浮筏隔振系统的一阶共振频率与二阶共振频率约为5Hz和19Hz。本文选取的激励信号为:
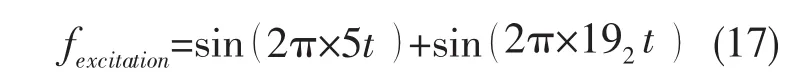
从(9)式可以看出,在同一个输入激励信号作用下,对无控制作用的最优被动阻尼系统与半主动模糊PID控制下的浮筏隔振系统来说,由于所产生的上层质量的加速度是不同的,所以对两个系统所产生的输入激励力是不同的,因而不能单独以两个不同系统在同一个输入激励信号作用下的输出力响应曲线来判断各个系统的隔振效果。为此,当输入为激励信号而不是直接为激励力的情况下,下面的仿真给出了无控制作用的最优被动阻尼系统与半主动模糊PID控制下的隔振系统在(17)式所示的双频激励信号下的输入力及输出力曲线,持续时间都为2 s。
图10与图11分别为双频信号激励下最优被动阻尼系统与半主动模糊PID控制下的隔振系统的输入力及输出力曲线。从图10-11中可以看出,相对于最优被动阻尼系统的输出力比输入力幅度的降低,半主动模糊PID控制下的隔振系统的输出力比输入力有更大幅度的减小,为此说明半主动模糊PID控制下的隔振系统减振效果要明显好于最优被动隔振系统。
4 结 语
对带有电流变液智能阻尼器的双层浮筏隔振系统设计了半主动模糊PID控制控制器。仿真分析了多种激励下浮筏隔振系统的输出力响应。仿真结果表明:与最优被动阻尼和电流变液阻尼器最大阻尼相比,模糊PID控制下的半主动浮筏隔振系统的减振效果最好。
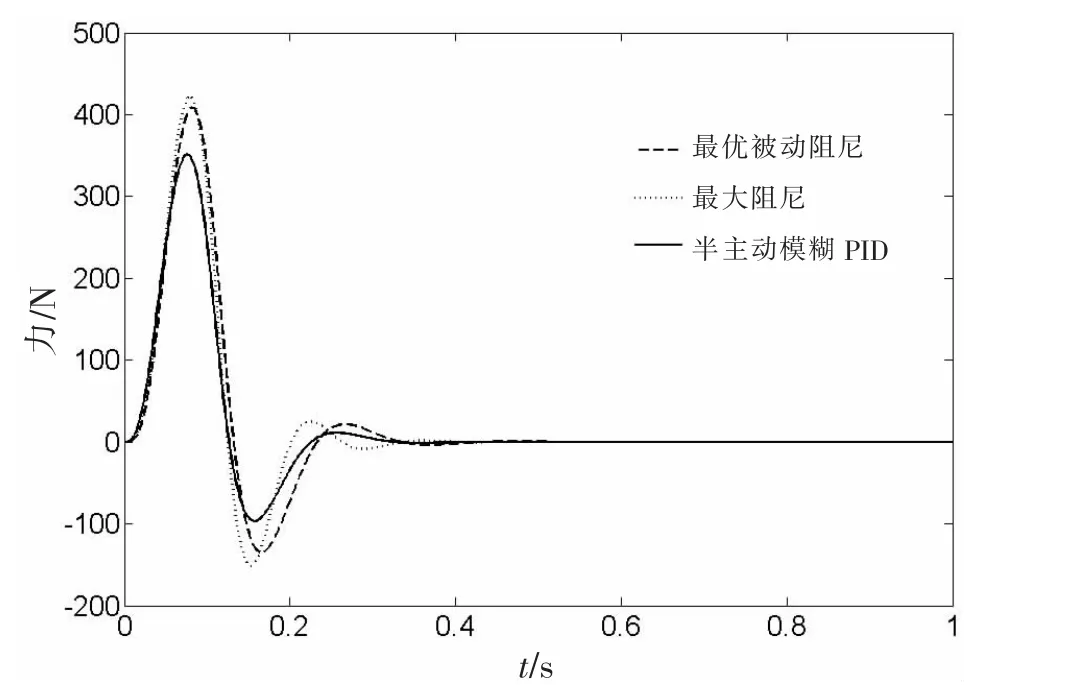
图9 半波正弦激励下浮筏隔振系统的输出力响应曲线Fig.9 Output force response of floating raft isolation system to a single bump excitation
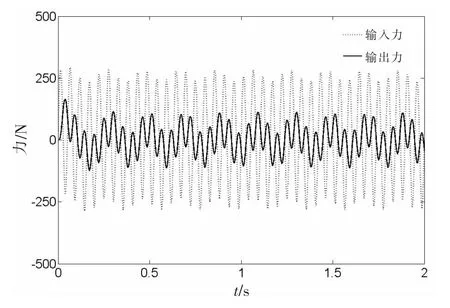
图10 双频信号激励下最优被动浮筏隔振系统的输入力及输出力曲线Fig.10 Input force and output force response of optimal damping floating raft isolation system to dualfrequency signal excitation
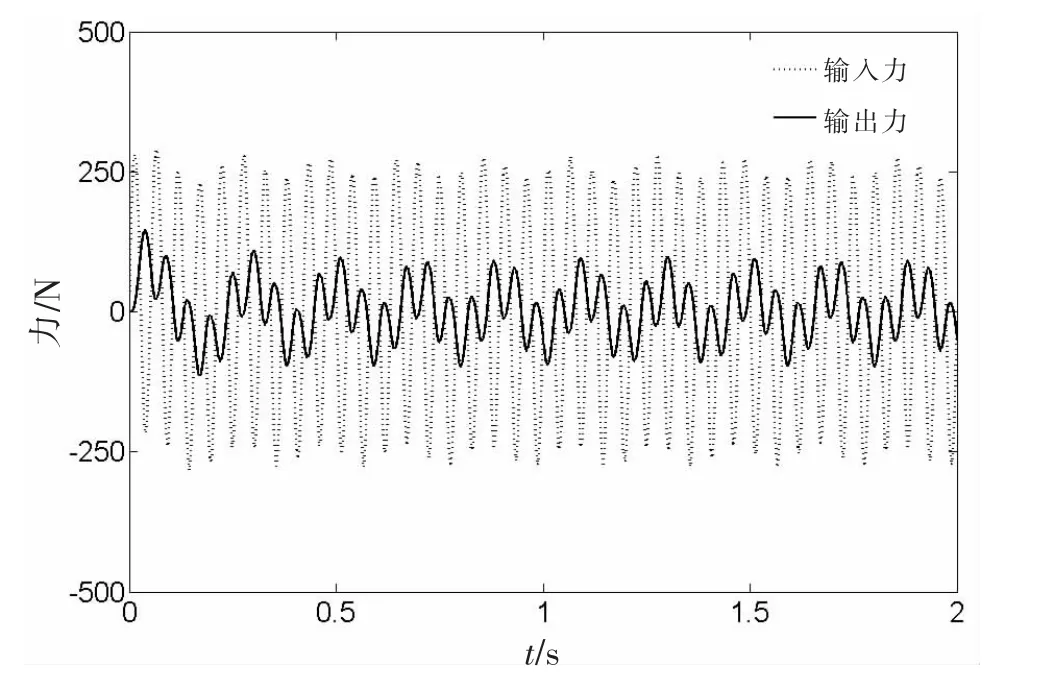
图11 双频信号激励下半主动模糊PID控制浮筏隔振系统的输入力及输出力曲线Fig.11 Input force and output force response of semi-active fuzzy-pid floating raft isolation system to dualfrequency signal excitation
[1]许树浩,桂洪斌.浮筏系统隔振性能的功率流评价指标[J].船舶力学,2012,16(5):567-572.Xü Shuhao,Gui Hongbin.Power flow estimation of float raft isolation system[J].Journal of Ship Mechanics,2012,16(5):567-572.
[2]张树桢,陈 前.柔性浮筏隔振系统的理论建模与仿真研究[J].船舶力学,2012,16(10):1187-1198.Zhang Shuzhen,Chen Qian.Modeling and simulation research on flexible floating raft isolation system[J].Journal of Ship Mechanics,2012,16(10):1187-1198.
[3]Choi S B,Kim W K.Vibration control of a semi-active suspension featuring electrorheological fluid dampers[J].Journal of Sound and Vibration,2000,234(3):537-546.
[4]朱石坚,何 琳.双层隔振系统隔振效果研究[J].海军工程大学报,2002,14(6):6-9.Zhu Shijian,He Lin.Study on the vibration-isolation effect of double-stage vibration-isolation systems[J].Journal of Naval University of Engineering,2002,14(6):6-9.
[5]Lin Y J,Lu Y Q,Padovan J.Fuzzy logic control of vehicle suspension systems[J].International Journal of Vehicle Design,1993,14(5/6):457-470.
[6]Zhao Z Y,Satoru I.Fuzzy gain scheduling of PID controllers[J].IEEE Transactions on Systems,Man,and Cyberntics,1993,23(5):1392-1398.
[7]汪建晓,孟 光.磁流变液阻尼器用于振动控制的理论及实验研究[J].振动与冲击,2001,20(2):39-45.Wang Jianxiao,Meng Guang.Theoretical and experimental study on the vibration control by magneto-rheological fluid dampers[J].Journal of Vibration and Shock,2001,20(2):39-45.
Fuzzy-PID control for semi-active floating raft isolation system
ZHAO Cheng
(Dept of Automation,Suzhou Vocational University,Suzhou 215104,China)
A fuzzy-PID controller is designed for semi-active floating raft isolation system featuring electro-rheological(ER)damper.The inputs of the fuzzy controller are the deviation of the intermediate mass displacement and its derivative,while its outputs are proportional,integral,and derivative gains of PID controller.The vibration of the intermediate mass is reduced because of the damping force varying with different voltage.The output force responses of floating raft isolation system acted by many kinds of excitations are simulated.The simulation results indicate that the performance of semi-active floating raft isolation system designed with fuzzy-PID method is remarkably better than that of optimally passive damping and maximal damping.
semi-active;floating raft;fuzzy-PID
O328 TB535
A
10.3969/j.issn.1007-7294.2017.10.013
1007-7294(2017)10-1291-08
2017-05-19
江苏高校哲学社会科学研究项目(2015SJD575);江苏高校品牌专业建设工程资助项目(PPZY2015A089);苏州市职业大学校级课题(2014SZDCC07)
赵 成(1974-),男,博士,E-mail:zhaoc@jssvc.edu.cn。

