一种基于兴趣挖掘的机会网络内容分发策略

孙立奋, 潘达儒

(华南师范大学物理与电信工程学院， 广州 510006)

一种基于兴趣挖掘的机会网络内容分发策略

孙立奋, 潘达儒*

(华南师范大学物理与电信工程学院， 广州 510006)

提出了一种新的基于兴趣挖掘的机会网络内容分发策略(Interest Mining Based Scheme,IMBS),通过贝叶斯理论分析节点的兴趣以及节点基于兴趣的相遇频率,挖掘移动节点随机运动背后所蕴含的人类社交特征和情感特征. 此外,IMBS采用发布/订阅机制,收集节点的订阅信息,以获取消息在整个网络中的需求量. 在转发消息的时候,IMBS把消息的需求总量和节点的情感特征以及社交特征结合起来选择下一跳节点. 仿真实验及算法复杂度分析表明,在不提高算法复杂度的情况下，IMBS可显著减少消息的传输延时和网络开销,并提高消息传输的成功率.

机会网络； 内容分发； 兴趣挖掘； 贝叶斯理论； 订阅/发布机制

Keywords： opportunistic networks; content dissemination; interests mining; Bayesian theory; publish/subscribe

随着大数据时代的到来,无线资源紧缺的问题日益显著,机会网络下的内容分发备受关注. 机会网络不要求源节点与目的节点之间存在着完整路径,通过节点移动带来的相遇机会实现网络通信[1-5]. 在这种动态拓扑的网络中，如何高效转发消息是亟待解决的问题. 针对该问题,相关的研究主要基于节点间的相遇频率和节点的兴趣.

基于节点间相遇频率的研究已经比较成熟,常见的有经典路由算法[6-9]以及基于社区理论的算法[10-13]. 例如,Epidemic算法[6]利用节点的相遇将消息泛洪,SprayAndWait算法[7]选取前n个相遇的节点转发消息，控制消息的副本数,Prophet算法[8]利用节点间的相遇概率转发消息；Maxprop[9]算法也是基于相遇概率.

基于节点兴趣的研究主要根据节点的兴趣推送消息[14-15]，如：PrefCast算法基于节点的兴趣转发消息,以便满足更多节点的兴趣需求[14].

为了吸取这2类算法的优点,学者们试图结合节点的相遇频率和兴趣选取下一跳节点[16-17]. 其基本思路是：把节点分成兴趣组和本地组，在转发消息的时候,优先选取和目的节点存在共同兴趣和社区的节点作为消息的携带者. 然而，即便是同属于一个社区又有共同兴趣爱好,这些节点也有概率处于该社区不同的地方,从而导致消息无法传递到目的节点. 所有的这些研究方法,仅仅是利用节点兴趣或者节点所处的地理社区,并没有根据这些兴趣以及地理社区深入挖掘其中所蕴含的人类活动特征和情感特征，难以有效分发内容.

基于此，本文提出了一种新的基于兴趣挖掘的机会网络内容分发策略(Interest Mining Based Scheme,IMBS)，充分考虑了节点兴趣、节点活动以及消息需求量等因素,通过贝叶斯理论对节点的活动以及节点的兴趣进行分析,挖掘节点活动的人类社交特征和情感特，并以此选择出一个合适的节点进行消息转发；通过仿真实验比较IMBS与Epidemic、SprayAndWait、Prophet、Maxprop路由算法在网络延迟、网络消耗以及消息传输成功率等方面的性能,并分析这些算法的复杂度，从而验证了IMBS的有效性.

1 内容分发策略的设计与实现

在介绍IMBS策略之前,先给出IMBS所使用的新概念、内容分发网络模型、相关假设及标注和相关计算.

1.1 相关概念的定义

(1)朋友圈：存在共同兴趣的两节点相遇时,节点此时所处的活动圈子称作朋友圈,用F表示. 一般而言，朋友间最大的特点就是存在共同兴趣，本文以共同兴趣这个特征表示朋友关系. 此外，本文研究的是节点活动的社交圈子,则相遇的朋友才有研究价值.

(2)熟人圈：不存在共同兴趣的两节点经常相遇时,节点此时所处的活动圈子称作熟人圈,用A表示. 一般而言，不管是否存在共同兴趣,熟人间经常会相遇. 因此本文把经常相遇抽取为熟人之间最大的特征. 同时为了与朋友圈区分,本文假设熟人之间不存在共同兴趣.

(3)陌生圈：不存在共同兴趣的两节点偶然相遇时,节点此时所处的活动圈子称作陌生圈,用S表示. 一般而言,偶然相遇是陌生人之间最大的特征.为了与朋友圈区分,本文假设所有的陌生人都不存在共同兴趣.

1.2 内容分发网络模型

基于大学校园构建机会网络内容分发网络模型，主要由网关、静止节点及移动节点等3类节点组成(图1). 移动节点代表网络用户,随机分布在网络的各个地方；静止节点分布在各个社区中,如图书馆、教学楼等.

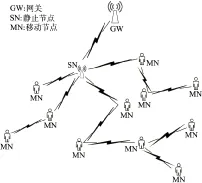
图1 网络模型

不同类型的节点负责网络不同的任务. 简而言之,网关负责接受来自静止节点的订阅消息,并且根据订阅产生相应的消息,满足用户的需求. 静止节点分散在整个网络的各处：一是为了收集来自移动节点的订阅消息,使得节点在不同的地方都可以提交自己的订阅消息；二是为了更好地把消息转发出去,满足更多移动节点的需求. 移动节点则根据自己的兴趣设置订阅消息. 在移动的过程中,每当遇到其他移动节点,移动节点将会相互协助转发订阅信息,以便更快地向网络提交或获取订阅消息.

1.3 假设及标注

(1)X表示移动节点当前的活动状态.

(2)假设节点在开始时处于3个圈子的概率相等,即1/3.

(3)每个节点都维护1个兴趣列表和2个普通列表,分别用I、O1、O2来表示.I用来存储当前移动节点订阅的消息，O1用来存储首次遇到的其他节点的订阅消息,O2用来存储多次遇到的其他节点的订阅消息.

(4)用MIi表示遇到其他移动节点的数量,且这些移动节点都对兴趣列表I中第i个消息感兴趣；同理,用MO1i表示遇到其他移动节点的数量,且这些移动节点都对普通列表O1中第i个消息感兴趣；用MO2i表示遇到其他移动节点的数量,而且这些移动节点都对普通列表O2中第i个消息感兴趣.

(5)用RIi表示兴趣列表I中第i个消息在整个网络中的需求量,用RO1i表示普通列表O1中第i个消息在整个网络中的需求量,用RO2i表示普通列表O2中第i个消息在整个网络中的需求量.

(6)每个节点维护一个消息列表,记为Mes,存储其他节点所感兴趣的消息,以帮助其他节点转发消息.

(7)每一个消息都维护一个订阅列表,记为P,用以记录对该消息订阅的移动节点.

(8)对于一个连接,把连接发起者的兴趣列表和2个普通列表分别记作SI、SO1和SO2；把连接接受者的兴趣列表和2个普通列表分别记作RI、RO1和RO2.

1.4 概率计算

由于移动节点在网络中移动,不同时刻可能处于不同的活动圈子. 而节点的3个活动圈子是相互独立的,本文根据贝叶斯定理实时计算节点在各个活动圈子的概率,以此实时判断节点所处的活动圈子,从而选取出适合转发消息的节点.

当移动节点处于活动状态X时,由贝叶斯定理可知,该移动节点处于朋友圈的概率为

(1)

该节点处于熟人圈的概率为

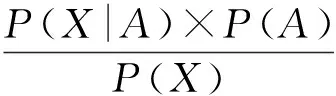
(2)

该节点处于陌生圈的概率为

(3)

由式(1)～(3)可知,状态X出现的概率P(X)对于所有类别都一样. 而本文所研究的活动圈子是单属性的,由此可得

P(X|F)=P(X|A)=P(X|S)=1.

(4)

由式(1)～(4)可得,节点在状态X的条件下处于各个圈子的概率的相对大小可以通过节点在各个圈子的概率来比较,即P(F)、P(A)和P(S). 下面,本文根据节点的历史活动估算节点在各圈子的概率.

假设兴趣列表I中存在NI个消息,普通列表O1中存在NO1个消息,O2中存在NO2个消息,则该节点在朋友圈中遇到的节点总数为

(5)

该移动节点在熟人圈中遇到的节点总数为

(6)

该移动节点在陌生圈中遇到的节点总数为

(7)

由式(5)～(7)可知,该移动节点在朋友圈中出现的概率为

(8)

该移动节点在熟人圈中出现的概率为

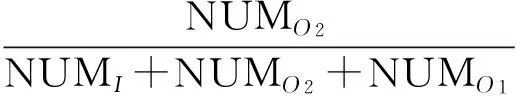
(9)

该移动节点在陌生圈中出现的概率为

(10)

因此,通过比较P(F)、P(A)及P(S)的大小就可判断节点此时所处的社交圈子.

1.5 效用值函数

在实际的网络中,一个移动节点可携带多个消息,一个消息可被多个节点所订阅,而处于朋友圈、熟人圈和陌生圈的节点可能有多个. 为了选择出一个更适合转发消息的节点,本文基于消息在整个网络的需求以及节点所处的社交圈子提出效用函数.

1.5.1 朋友圈效用函数 当邻居节点中存在多个节点对源节点所携带的消息感兴趣,而且都处于朋友圈，则朋友圈效用函数G=RIi×P(F). 可知,当节点在它的朋友圈的活跃度P(F)越大,消息的需求量RIi越大,则该节点可以更短的时间满足更多节点的订阅需求,因此朋友圈效用也就越高.

1.5.2 熟人圈效用函数 当邻居节点中不存在任何节点对中间节点所携带的消息感兴趣,但是邻居节点熟人圈中存在对中间节点所携带的消息感兴趣的节点,则熟人圈效用函数H=RO2i×P(A). 可知,当节点在熟人圈中的活跃度P(A)越高,消息的网络需求量RO2i越大,则该节点可以更短的时间满足更多节点的需求,因此该节点所处的熟人圈的效用也越高.

1.5.3 陌生圈效用函数 当接受者的朋友圈和熟人圈都不存在节点对中间节点所携带的消息感兴趣,则陌生圈效用函数J=RO1i×P(S). 可知,当节点在陌生圈中越活跃,即遇到的陌生节点越多,消息的需求量越大,则有更大的概率成功转发消息，因此,陌生圈的效用也就越大.

1.6 内容分发策略

本文所提出的IMBS是基于发布/订阅机制的,包含消息的订阅过程和分发过程.

1.6.1 订阅过程 主要完成移动节点对消息的订阅,实现过程如下：

if (发起连接)

if (发起者是移动节点) //移动节点

if (接受者是移动节点)

fo r (SI中的每一个消息id)

i f (RI中包含id)

把接受者添加到该id的P列表；

MIi++；

els e if (RO2中包含id)

MO2i++；

else if (RO1中包含id)

MO2i++；

把id添加到RO2中；

RO1列表删除该id；

else

MO1i++；

把id添加到Ro1中；

end if

end for

else if (接受者是静止节点)

向静止节点订阅消息.

end if

else if(发起者是静止节点)//静止节点

if (收到移动节点新的订阅信息)

向网关订阅信息;

end if

else if(发起者是网关)//网关

if (收到静止节点新的订阅信息)

根据订阅产生新的消息；

删除订阅列表中相应的id；

end if

end if

end if

节点在订阅的过程中,算法也会收集一些网络信息,比如消息的需求量、节点与节点之间的兴趣以及相遇情况等,并利用这些信息动态识别移动节点的活动圈子,以便更好地为内容分发做准备.

1.6.2 分发过程 主要把各个消息分发到各个订阅者,其实现过程如下：

for(每一个连接)//获取有效的连接

for(发起者缓存列表每一个消息)

//缓存列表存储别人订阅的消息

if(接受者缓存列表Mes有该消息)

Continue；

else if(接受者接受列表有该消息)

//接受列表存储自己订阅的消息

Continue；

end if

把消息及连接添加到Sending列表；

//Sending 列表为待转发列表

end for

end for

Sending列表按消息效用值降序排序；

for (Sending列表中的每一个值)

if (传输完毕)

消息传输成功;

else if (掉包)

存储空间不足,需要缓存管理.

下一个待转发的连接；

end if

if (缓存不足) //缓存管理

按消息效用值对Mes排序；

删除Mes中效用值最低的消息;

end if

end for

在分发消息时,按照节点的兴趣以及节点所处的社交圈子转发消息. 简而言之,如果邻居节点都对消息感兴趣,优先把消息分发给处于朋友圈的节点,然后是处于熟人圈的节点,最后是处于陌生圈的节点. 对于处于同一个圈子的节点,将按照效用值的大小先后转发. 但如果不存在对消息感兴趣的节点,则只把消息转发给处于熟人圈和陌生圈的节点,因为处于朋友圈的节点很难遇到与自己不存在共同兴趣的节点,从而难以将消息转发给订阅者. 这样就避免了无效消息的产生,减少网络开销. 为了进一步管理缓存,本文限制每个消息的生命周期,并且假定缓存容量有限,只有效用值较大的消息才能缓存到消息列表.

2 仿真实验

在机会网络仿真平台ONE中对IMBS、Epidemic、SprayAndWait、Prophet和Maxprop路由算法进行了仿真实验，并从传输延迟、网络消耗量以及传输成功率等3个方面进行比较. 仿真测试环境如下：网关1个,静止节点8个,移动节点176个,移动节点运动速度0.7～4 m/s,节点缓存容量大小为50 M.

2.1 传输延迟

图2显示了IMBS与其他路由算法在消息传输延迟方面的比较. 在整个仿真过程中,IMBS算法的传输延迟低且稳定,比传统最优的MaxProp算法平均还要低71.9%. 这主要有两方面的原因：(1)IMBS算法根据消息的网络需求量、节点的兴趣以及节点的活动圈子转发消息,能够迅速地把消息分发给订阅者；(2)IMBS算法根据用户的兴趣分发消息,因此一个消息可以满足多个用户的需求,从而大大减少网络延迟.

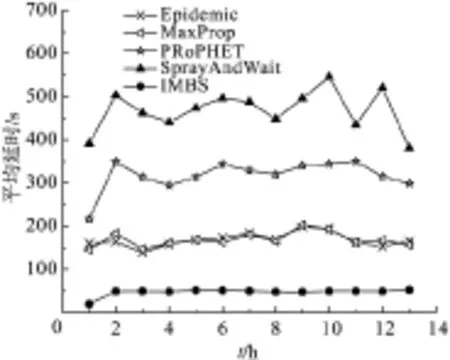
图2 各种路由算法的平均延迟

2.2 网络开销

图3显示了IMBS算法与其他路由算法在网络开销方面的比较. 在整个仿真过程中,IMBS的网络开销与MaxProp算法的相似,但远低于Epidemic算法和Prophet算法. 这主要是因为IMBS算法设定了每个消息的生命周期以及缓存容量,并根据节点的活动圈子避免无效的消息转发以及及时清理缓存列表中的无效消息. 而SprayAndWait算法的网络开销最低,这主要是因为该算法强制控制消息副本的数量,防止消息泛洪.

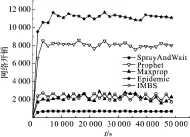
图3 各种路由算法的网络开销

2.3 传输成功率

如图4所示,与MaxProp算法和Prophet算法相比,IMBS算法在仿真开始时消息转发成功率波动比较大. 这主要有两方面的原因:(1)移动节点在网络中动态订阅消息,消息订阅不稳定；(2)消息达到生命周期就会消失. 但是随着时间的转移,IMBS算法在传输成功率方面趋于稳定,而且远远优于Epidemic算法和SprayAndWait算法,并且接近MaxProp算法和Prophet算法.

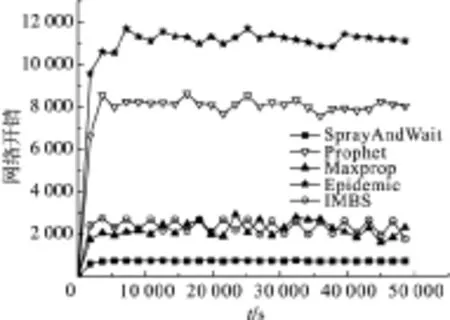
图4 各路由算法的传输成功率

3 算法复杂度分析

本文所设计的IMBS算法与其他4种经典路由算法都是在ONE平台上实现的,因此只讨论路由算法方面的算法复杂度. IMBS算法主要分为信息收集的订阅过程和转发消息的分发过程. 因此，也将从这2个方面分析算法的时间复杂度和空间复杂度.

3.1 时间复杂度

在信息收集方面,IMBS算法、MaxProp算法及Prophet算法需要收集节点的历史数据信息,而SprayAndWait算法和Epidemic算法不需要收集历史数据. 因此，SprayAndWait算法和Epidemic算法在信息收集方面的时间复杂度为Ο(1). 对于本文所提出的IMBS算法,如第1.6.1节订阅过程的伪代码,算法的时间复杂度主要由一个for循环和一个查询语句决定,for循环是遍历节点的兴趣列表,由于IMBS算法限定移动节点每次最多可以订阅的消息数,因此该for循环的复杂度为Ο(1). 而查询语句是Java内置的List列表中的contain函数,属于线性查询,最坏时间复杂度为Ο(n)，最好时间复杂度为Ο(1). 由于每个节点设置订阅消息是随机的，假设节点订阅每个消息的概率相等,则该查询的平均复杂度为Ο(n(n+1)/(2n))=Ο(n). 因此,IMBS算法订阅过程在最坏的情况下,时间复杂度为Ο(n),平均复杂度为Ο(n)，最好的情况下是Ο(1). 通过分析MaxProp算法以及Prophet算法的源代码可知,MaxProp算法以及Prophet算法的时间复杂度由一个for循环决定,遍历整个列表,因此MaxProp算法以及Prophet算法在收集信息方面的时间复杂度在最好、最坏及平均的情况皆为Ο(n)(表1).

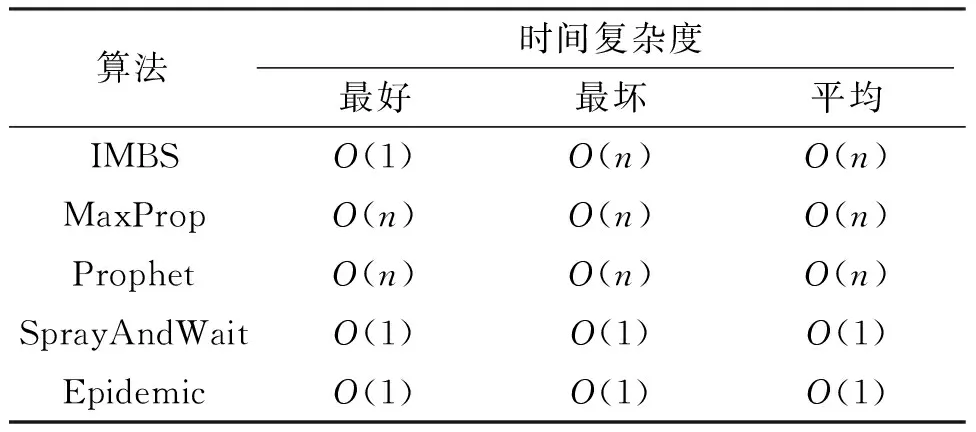
表1 各算法订阅过程的时间复杂度Table 1 Time complexities of algorithms in subscription process

在分发过程,IMBS算法与MaxProp算法、Prophet算法相似,只是在对Sending列表的排序以及缓存管理策略有所不同. 在获取待转发连接中,涉及2个for循环以及一个线性查询(分发过程第1、2、4行代码),因此，时间复杂程度在最坏的情况下为Ο(n3)，最好的情况下为Ο(n2). 假设每次要查询的消息出现的概率相等，则平均情况下也为Ο(n3). Sending列表的排序时间复杂度远低于Ο(n3)，缓存管理策略只需遍历一次缓存列表即可. SprayAndWait算法和Epidemic算法的分发过程也类似. 通过分析这2种算法在消息分发部分的源代码,虽然不存在对Sending列表的排序,但是发现其存在3个嵌套型for循环进行遍历,因此在最好、最坏及平均情况下，时间复杂度都为Ο(n3)(表2).

表2 各算法分发过程的时间复杂度Table 2 Time complexities of algorithms in publishing process

3.2 空间复杂度

空间复杂程度是对一个算法在运行过程中占用存储空间大小的量度，也是问题规模n的函数,其中所占用的存储空间包括固定空间与可变空间. 但是由于机会网络路由算法研究的是消息的传输，需要缓存消息，可变部分远远大于固定部分，因此，本文主要分析可变部分，而可变部分表现在信息收集过程和消息缓存过程.

在信息收集过程，通过分析算法源代码可知，SprayAndWait算法和Epidemic算法在信息收集过程没有收集任何信息，不存在空间复杂程度问题. IMBS算法只需要遍历有限的兴趣列表，空间复杂程度为Ο(1).而MaxProp算法和Prophet算法不存在for循环，空间复杂程度为Ο(1).

在消息分发过程，IMBS算法与MaxProp算法、Prophet算法相似，空间复杂度主要由获取待转发连接过程和存储消息过程决定. 在对Sending队列进行添加操作时经历了2个for循环，如分发过程中的第1、2、14行所示，因此空间复杂度为Ο(n2). 消息传输完毕需要存储消息，如分发过程的第18、20行所示，这个存储过程的空间复杂度为Ο(n). 而SprayAndWait算法与Epidemic算法的空间复杂程度主要由存储过程决定，也是Ο(n). 在存储过程中，由于存储的是消息,占用空间资源量比较大,超过了Sending队列的添加操作，故存储过程决定了整个算法的存储空间的消耗. 因此，各算法的缓存管理策略决定了该算法的空间资源开销. 各算法在分发过程的空间复杂度见表3.

表3 各算法分发过程空间复杂度Table 3 Space complexities of algorithms in publishing process

4 结论

本文通过节点的兴趣与节点运动分析出节点的活动圈子,在看似毫无规律的运动中找出移动节点的人类活动特征和情感特征,进而为选择一个合适的节点进行内容分发提供了一种方法. 仿真实验表明,与传统路由算法相比,IMBS算法显著降低了消息传输的平均延迟,并且把网络开销和消息传输成功率控制在一定范围内,具有一定的可行性和有效性.

[1] 潘达儒,麦立峰,齐小宇. 机会计算研究综述[J]. 华南师范大学学报(自然科学版),2016,48(5):116-122.

PAN D R,MAI L F,QI X Y. Survey on opportunistic computing[J]. Journal of South China Normal University(Natural Science Edition),2016,48(5):116-122.

[2] PELUSI L,PASSARELLA A,CONTI M. Opportunistic networking:data forwarding in disconnected mobile ad hoc networks[J]. IEEE Communications Magazine,2006,44(11):134-141.

[3] WANG Y,JAIN S,MARTONOSI M,et al. Erasure-coding based routing for opportunistic networks[C]//Proceedings of the 2005 ACM SIGCOMM Workshop on Delay-tolerant Networking. New York:ACM,2005:229-236.

[4] RAMANATHAN R,HANSEN R,BASU P,et al. Prioritized epidemic routing for opportunistic networks[C]//Proceedings of the 1st International MobiSys Workshop on Mobile Opportunistic Networking. New York:ACM,2007:62-66.

[5] YOUNIS O,FAHMY S. HEED:a hybrid,energy-efficient,distributed clustering approach for ad hoc sensor networks[J]. IEEE Transactions on Mobile Computing,2004,3(4):366-379.

[6] VAHDAT A,BECKER D. Epidemic routing for partially-connected ad hoc networks[D]. Durham:Duke University,2000.

[7] SPYROPOULOS T,PSOUNIS K,RAGHAVENDRA C S. Spray and wait:an efficient routing scheme for intermittently connected mobile networks[C]//Proceedings of the 2005 ACM SIGCOMM Workshop on Delay-Tolerant Networking. New York:ACM,2005:252-259.

[8] LINDGREN A,DORIA A,SCHELÉN O. Probabilistic routing in intermittently connected networks[J]. ACM SIGMOBILE Mobile Computing and Communications Review,2003,7(3):19-20.

[9] BURGESS J,GALLAGHER B,JENSEN D,et al. MaxProp:routing for vehicle-based disruption-tolerant networks[C]// Proceedings of 25th IEEE International Conference on Computer Communications. Barcelona:IEEE,2006:1-11.

[10] XIAO M,WU J,HUANG L. Community-aware opportu-nistic routing in mobile social networks[J]. IEEE Transactions on Computers,2014,63(7):1682-1695.

[11] NIU J,ZHOU X,WANG K,et al. A data transmission scheme for community-based opportunistic networks[C]// Proceedings of the 5th International Conference on Wireless Communications,Networking and Mobile Computing. Beijing:IEEE,2009:1-5.

[12] LI F,ZHAO L,ZHANG C,et al. Routing with multi-level cross-community social groups in mobile opportunistic networks[J]. Personal and Ubiquitous Computing,2014,18(2):385-396.

[13] NIU J W,WU F F,HUO D,et al. Message publish/subscribe scheme based on opportunistic networks[C]// Proceedings of the 2010 Symposia and Workshops on Ubiquitous,Autonomic and Trusted Computing. Xi’an:IEEE,2010:180-184.

[14] LIN C J,CHEN C W,CHOU C F. Preference-aware content dissemination in opportunistic mobile social networks[C]∥Proceedings of the 31st Annual IEEE International Conference on Computer Communications. Orlando:IEEE,2012,131(5):1960-1968.

[15] GREIFENBERG J,KUTSCHER D. Efficient publish/subscribe-based multicast for opportunistic networking with self-organized resource utilization[C]// Proceedings of the 22nd International Conference on Advanced Information Networking and Applications-Workshops. Okinawa:IEEE,2008:1708-1714.

[16] PATEL J A,RIVIERE E,GUPTA I,et al. Rappel:exploiting interest and network locality to improve fairness in publish-subscribe systems [J]. Computer Networks,2009,53(13):2304-2320.

[17] JAHO E,STAVRAKAKIS I. Joint interest- and locality-aware content dissemination in social networks[C]//Proceedings of the Sixth International Conference on Wireless On-Demand Network Systems and Services. Snowbird:IEEE,2009:161-168.

An Opportunistic Network Content Distribution Strategy Based on Interest Mining

SUN Lifen, PAN Daru*

(School of Physics and Telecommunication Engineering, South China Normal University, Guangzhou 510006, China)

A new interest mining based scheme(IMBS) is proposed. In IMBS, the interest and meeting frequency are analyzed based on interest of mobile nodes according to Bayesian theory, to find out the human social and emotional characteristics behind the random movement of the mobile nodes. In addition, the publish/subscribe mechanism is adopted to collect the node’s subscription information, in order to obtain the total demand of messages in the whole networks. When forwarding a message, the total demand of messages with the emotional characteristics and the social characteristics of the nodes are combined to select the next-hop node. The results of simulation experiment and the analysis of complexities of algorithms show that IMBS can significantly reduce the message delivery delay and network overhead, and improve the delivery ratio of message transmission without increasing the complexity of the algorithm.

2017-01-22 《华南师范大学学报(自然科学版)》网址：http://journal.scnu.edu.cn/n

国家自然科学基金项目(61471175)；教育部新世纪优秀人才支持计划项目(NCET-13-0805)

*通讯作者:潘达儒,教授,Email:pandr@scnu.edu.cn.

TP393

A

1000-5463(2017)05-0108-07

【中文责编：庄晓琼 英文审校：肖菁】