指数律参数选取对指数和廓线精度的影响

齐宏纲， 孙 武*， 李庆祥， 黄启明， 黄 盛， 江云峰， 梁幸怡

(1. 华南师范大学地理科学学院， 广州 510631； 2. 广东省建筑科学研究院集团股份有限公司风工程研究中心， 广州 510500)

指数律参数选取对指数和廓线精度的影响

齐宏纲1， 孙 武1*， 李庆祥2， 黄启明2， 黄 盛1， 江云峰1， 梁幸怡1

(1. 华南师范大学地理科学学院， 广州 510631； 2. 广东省建筑科学研究院集团股份有限公司风工程研究中心， 广州 510500)

基于广州市主城区水平比例尺为1∶7 000和垂直比例尺分别为1∶500、1∶1 000、1∶2 000的三维建筑模型，在B类边界层中性流条件下进行风洞模拟. 利用26个测点、15个高度的西北和东南盛行风况下的风速数据，分析指数律参考高度zref、零平面位移d和采样厚度t等3个参数对指数α和拟合精度的不确定性影响，并为指数律应用中精度的提高提供了相应的建议. 实验结果表明：参考测点最高高度α的均值和离散度相对较小，且拟合较为理想；d的引入能提高拟合精度，且与α呈负相关；不考虑零平面位移d的指数律对下垫面非均质、测点众多的研究更为实际；不同粗糙程度的下垫面，α在0.25～1 H廓线厚度段内收敛，0.25～1 H是理想的采样厚度.

指数律； 指数； 零平面位移； 采样厚度； 拟合精度

Keywords： power law; exponent; zero-plane displacement height; sampling thickness; fitting precision

低层大气边界层风的特性对于建筑设计规划、污染物扩散和风能发电等具有重要意义[1]，大气指数风速剖面是研究典型地区风场特性及反映近地表下垫面动力属性的重要参考之一. 多年以来指数律因精度高、简单实用，在风速预报[2]、风能开发[3]和数值模拟等领域得到广泛应用. 大气层结稳定度[4]、雷诺系数[5]和热力属性等流场特性差异，粗糙元高度和宽高比等下垫面形态区别[4]，以及分析时段、土地特征和高度等测量条件[6]不同均会导致风速剖面指数值的波动变化.

指数律的实际应用中，对于参考高度zref、零平面位移d以及数据采样厚度t等3个参数的使用规范尚未达成学术共识：(1)参考高度zref的选取差异较大，缺少从指数值合理性及拟合精度视角确定参考高度zref的研究探讨，野外近地层实测由于气象站观测高度相对统一，多选用10 m作为参考高度[7-8]，也有参考测量最高高度分析指数廓线规律[9]. 风洞模拟参考高度的选择趋于边界层厚度，主要包括试验边界层厚度[10]，以及由同类下垫面野外边界层厚度(梯度风高度)按几何缩尺类推转化[11-12]，此外也有结合试验下垫面模型和粗糙元高度主观确定参考高度[13-14]，与试验边界层厚度、类型及几何缩尺比例等并无几何关系. (2)零平面位移d取值，及对指数值和拟合精度的影响尚不确定. 一方面，d与粗糙元高度存在一定的数量关系[15]；另一方面，d可等同于动力粗糙度z0[16]，代表下垫面对气流的阻滞作用. 指数律中d的增加会降低风速标准差和指数α[17]，但不影响拟合精度中的相关系数R[15],零平面位移d使用复杂性使得更多指数律应用并未考虑d[18-20]. (3)采样厚度t指测量剖面最高高度与最低高度的差，为获得理想廓线，在风洞和野外实测中常需增加测管高度或风速采样高度，采样厚度t常按粗糙元高度h或下垫面最高高度hmax无量纲化. 受技术和经济条件制约，采样厚度t更是薄厚不同，从低于粗糙元高度(0.35倍)[21]到高达其43倍[22]，鲜有分析指数值与采样厚度t间的变化关系、是否存在随厚度变化α不再变化的采样厚度.

针对指数律参考高度zref、零平面位移d与采样厚度t选取上的不确定性，本文基于水平比例尺为1∶7 000和垂直比例尺分别为1∶500、1∶1 000、1∶2 000概括的忽略地形的广州市主建成区三维建筑模型在B类中性流边界层进行风洞模拟，利用26个测点和15个测孔高度的西北和东南2种盛行风况下的风速数据，分析不同参考高度zref、零平面位移d与采样厚度t对指数α取值与拟合精度的影响，为指数律的规范化应用和提高拟合精度提供相应建议.

1 风洞模拟与数据处理

1.1 风洞选择与测量方法

风洞试验在广东省建筑科学研究院集团股份有限公司建筑风洞试验室进行，该风洞为串联双试验段回流式风洞，其试验段最大截面为3 m×2 m，风速最高可达46 m/s. 采用《建筑结构荷载规范》(GB 50009-2001)中规定的B类地貌大气边界层气流，风剖面指数α=0.16，边界层形成厚度δ为350 m. 根据广州的盛行风，确定2个模拟风向:西北与东南，且在不加建筑模型的情况下，在靠近来流位置测量了西北风向的标准风速剖面并与B类边界层风剖面对比验证，试验采用皮托管量测u分量风速. 26个试验测点的布置以纵横各5个并等距分布于平原、台地、峡谷和高原等建筑形成的城市地形之上，较好地代表了下垫面粗糙度的差异.

1.2 试验模型与数据处理

试验模型基于GoogleEarth影像，通过建筑物阴影长度与高度的线性相关，获取了2万多座建筑物的高度数据，并结合广州市土地利用图，以2 435个500 m×500 m的网格区域构建了2010年广州市不考虑地形条件下主体建筑的立体形态模型，模型代表广州市主城区南北22 404 m、东西21 228 m的空间范围.

试验模型有3个，水平比例尺均为1∶7 000，垂直比例尺分别为1∶500、1∶1 000与1∶2 000，模型最高高度分别为33、15、7.5 cm(图1)，对应实际模型的最高高度150 m. 广州市城市立体形态的历史演变体现在建成区平面的扩展[23]以及建筑高度的抬升两方面. 3个垂向比例尺的设定本质上反映了粗糙元宽高比的变化，反映了指数廓线对于不同时代、不同宽高比的城市地形的适用性. 参照以往风洞试验50个测点模拟结果，本次试验在提高模型概括精度基础上，选取了其中具有下垫面几何形态代表性的26个测点，具体编号详见图1.

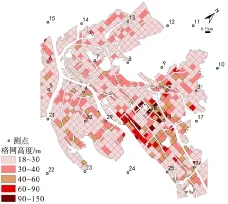
图1 风洞试验建筑模型测点分布

Figure 1 Distribution of measuring points of building model in wild tunnel test

指数律用来描述边界层垂向平均风速随高度变化的特征规律，1960年，DAVENPORT[24]依据多次观测资料整理出不同场地下的指数风剖面：

(1)

其中：zref和uref分别代表参考高度和参考高度处的平均风速，z和u(z)分别代表任一高度及该高度的平均风速，α为风速剖面指数.

类似对数律[25]，指数律可考虑零平面位移d，从而派生出以下2种变形指数律：

(2)

(3)

所用风速数据均不考虑回流段，1∶500模型由于粗糙元较高及测管厚度限制，在背风涡流区的一些测点回流厚度较厚，使得拟合正常流测孔数目较少(3个)，α均超过0.6，如西北风向25号和东南风向8号、13号测点，认为是无效数据，不进行分析，并且3个模型东南风向10号测点由于实验设备限制，未能测量其风速.

本文利用最小二乘法(LES)[26]拟合了不同垂向比例尺、不同风向的风剖面指数. 参数选取对α的影响通过α均值和α标准差来体现，精度用标准误差e的均值及相关系数R表示：

(4)

(5)

其中，vi(z)为i测孔z高度处LES计算所得风速理论值，ui(z)为i测孔z高度处实测风速值，n为测孔个数,zi为i测孔实测高度. 指数廓线精度筛选标准里，标准误差e、相关系数R和判定系数R2分别规定为e≤0.5、R≥0.95和R2≥0.902 5.

2 结果与分析

本节从确定4类参考高度和零平面位移d、推算收敛厚度并与全厚度进行比较等3个方面着手，分析参考高度zref、零平面位移d和采样厚度t的变化对α测量值(α标准差、α均值)和拟合精度(e均值和相关系数R)的具体影响.

2.1 参考高度

由式(5)知R只与zi和ui(z)有关，与zref和uref无关，故zref对α和拟合精度的影响不考虑精度标准中的R. 选取B类边界层标准剖面最高高度zref-sta及各模型测点剖面最高、中间、较低测孔所对应的最高高度zref-max、中间高度zref-mid、较低高度zref-min，利用式(1)，对比不同参考高度的α和拟合精度.

B类边界层标准剖面的最高高度zref-sta为60 cm，测点剖面的3个参考高度见表1. 梯度风高度(350 m)按垂直比例尺转化，梯度风参考高度zref-gra分别为70、35、17.5 cm. 故1∶1 000模型的zref-mid和1∶2 000模型的zref-min分别近似为各自的zref-gra. 结果表明，测点剖面的3个参考高度中，zref-max的α标准差、α均值相对较小，指数值更符合边界层规范(图2)，1∶500模型的α均值介于C类与D类边界层之间(0.22～0.30)，1∶1 000和1∶2 000模型的α均值处于B类与C类之间(0.16～0.22)，且随着垂直比例尺变大，α均值、α标准差逐渐减小，1∶1 000和1∶2 000模型的α标准差低于1∶500模型，都符合下垫面粗糙度逐渐减小的规律. 而西北风向的α标准差、α均值均低于东南风向，原因是东南风向下珠江新城(模型最高区域)更靠近来流风向，所形成的背风回流区域更大. 同时zref-max的e均值最小(图2)，拟合精度最高，其他2个参考高度的e均值偏大. 1∶1 000模型的zref-mid(zref-gra)和1∶2 000模型的zref-min(zref-gra)的α标准差、α均值和e均值均大于测点剖面zref-max，参考高度zref越高，风剖面特征属性越接近背景风，uref差异越小；测点剖面的zref-max与标准剖面的zref-sta相比，虽高度较接近，但后者的α标准差、α均值和e均值大于前者，拟合精度较差，α波动性大，两者的区别主要是参考风速值的差异，标准测点代表了B类边界层来流，而模型测点则反映了测点下垫面发育的边界层流场. 故选用测点最高高度zref-max为参考高度时，α均值和α标准差相对较小，且拟合精度最高.

表1不同模型测点剖面参考高度的取值范围

Table 1 Range of reference height of test points in different models cm

2.2 零平面位移

依据1∶500模型西北、东南风向各17个和18个测点的风速数据，分别赋值d=0、1.5、3、5、7、9.5、12 cm等7组来比较式(1)～(3)的α和拟合精度. 按1∶500模型最高粗糙元高度(30 cm)无量纲化后，d分别为0、0.05、0.10、0.17、0.23、0.32、0.40 H.d均满足低于廓线起始高度的条件，为增加1∶500模型可用分析测点廓线数量，把精度标准R调整为：R≥0.8，e保持不变.

图2 不同参考高度下的α标准差、α均值和e均值

Figure 2 The standard deviation ofα,the mean ofαand the mean ofein different reference heights

注：500 nw、500 se分别为西北和东南盛行风向下的1∶500垂直比例尺模型，其他类同.

测点廓线d与α的皮尔逊相关系数分别为-0.535 0和-0.370 1(表2)，负相关性显著，随着d的增大，式(3)和式(2)的α均值均减小，但相同试验条件下式(2)的α均值和α标准差要低于式(3)，并且随着d值的变大，两者的α均值和α标准差的差值也逐渐增加(图3)；随着d的增大，会提高式(3)和式(2)的精度标准中的相关性R(图4)，测点廓线d与R的皮尔逊相关系数均为0.253 1. 但两式表现有别，随着d增大，式(3)的标准误差e均值逐渐减小，但式(2)的e均值变化不大(图4). 总体上，含d的式(3)和式(2)精度要优于传统的指数律，特别是式(3)精度最高，且d也应该具有物理意义，近似等于建筑高度+回流厚度的高度面，在此高度面上发育的风廓线更能反映下垫面特征.

表2 1∶500模型不同指数律测点d与α、e、R相关性

Table 2 Each correlation betweendande,R,αin different power law at 1∶500 vertical scale

参数指数律式(2)指数律式(3)相关系数Rsig相关系数Rsigd与α-0.53500.0000-0.37010.0000d与e0.02550.7830-0.21880.0168d与R0.25310.00550.25310.0055

注：2种指数律廓线样本数量均为119条.

图3 1∶500模型不同指数律d与α均值、α标准差的关系

Figure 3 The relationship betweendand the mean ofα, the standard deviation ofαin different power law at 1∶500 vertical scale

图4 1∶500模型不同指数律d与R、e均值关系

Figure 4 The relationship betweendandR,emean in different power law at 1∶500 vertical scale

2.3 采样厚度

通过逐个去掉廓线顶部测孔来减小廓线厚度，利用式(1)来分析α随厚度的变化规律，确定两风向各模型测点的收敛厚度，所用廓线均满足精度筛选标准. 从上往下，随着采样厚度t变薄，存在指数逐渐收敛所对应的厚度，本文定义为收敛厚度，即指数变化在±0.01内的厚度. 全厚度指剔除掉回流测孔后，最高测孔与最低测孔的高度之差，反映的是测点一定范围内的下垫面特征. 收敛厚度廓线意味着可以用最小拟合高度段来代替全厚度廓线的拟合，表征了测点附近下垫面的属性. 研究发现：α随厚度减小呈微弱增加趋势，3个模型各风向收敛厚度廓线的α均值大于全厚度，且α增幅均小于0.01(表3)，底部厚度越薄，下垫面粗糙元对气流的阻滞作用越强，α越趋于增大. 测点全厚度与收敛厚度廓线的α十分接近(图5)，两风向各模型的收敛厚度廓线占全厚度廓线数量比均超过0.5(表3)，1∶2 000东南风向模型则达到0.96，基本能反映出整个下垫面的风廓线总体特征；随着模型垂向比例尺变小，按3个模型的hmax无量纲化后，廓线全厚度分别处于1～2、3～4、5～6 H的变化范围之内(图6). 不同粗糙程度的下垫面，收敛厚度基本小于2 H，且大部分处于0.25～1 H之间(图7)，占全厚度比最低40%，最高62%(表3). 因此，0.25～1 H可认为是理想的推荐采样厚度，收敛厚度除体现指数数学规律外，更反映了测点附近下垫面对廓线作用的高度范围.

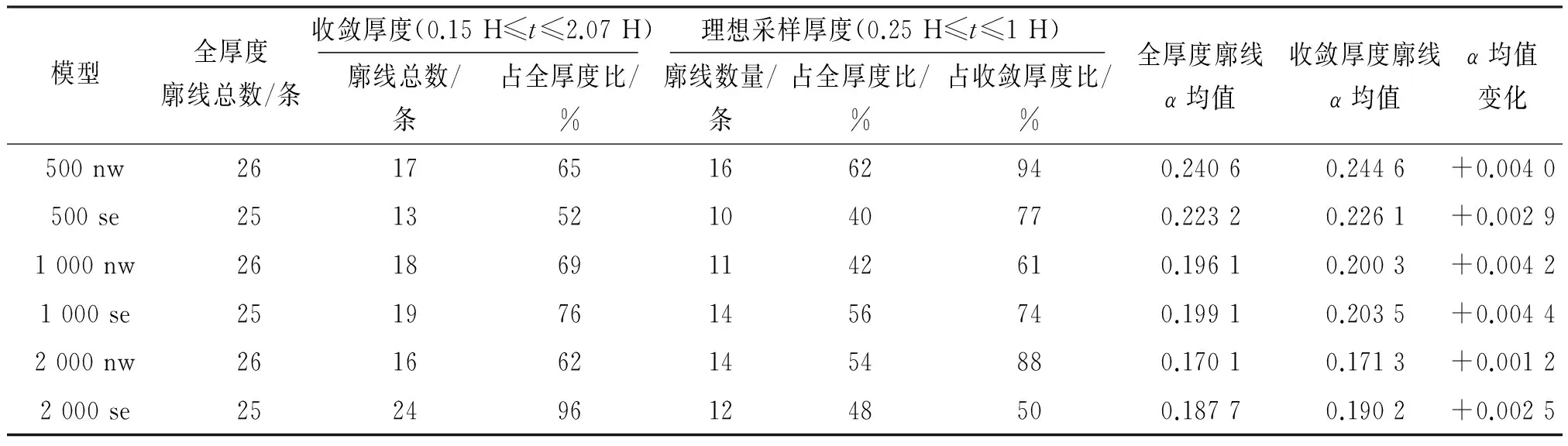
表3 全厚度、收敛厚度与推荐的采样厚度的廓线数量与α均值Table 3 The number of profiles and the mean value of α in full, convergent and recommended sampling thickness

注∶500 nw、500 se分别为西北和东南盛行风向下的1∶500垂直比例尺模型，其他类同. “+”代表指数α增加.

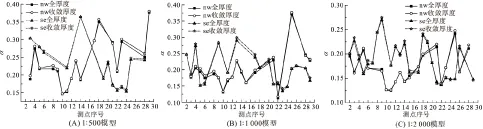
图5 全厚度与收敛厚度廓线α对比

图6 测点全厚度廓线厚度分布范围

Figure 6 The thickness range of full thickness profiles of test points

图7 测点收敛厚度廓线厚度分布范围

Figure 7 The thickness range of convergent thickness profiles of test points

3 结论与讨论

本文基于不考虑下垫面地形的水平比例尺为1∶7 000，垂直比例尺分别为1∶500、1∶1 000、1∶2 000概括的广州市主建成区三维建筑模型，利用26个测点和15个测孔高度的西北和东南2种盛行风况下的风速数据，分析不同参考高度zref、零平面位移d与采样厚度t对指数α与拟合精度的影响，主要结论有：

(1)参考高度zref的不同对指数α有一定影响，野外实测多采用气象站10 m高度风速数据，而风洞试验包括来流边界层厚度、梯度风高度按几何缩尺转化高度、测点高度等多种参考高度，研究发现参考高度为测点最高高度zref-max时，拟合精度最高，α的均值和离散度相对较小，而以梯度风高度转化高度zref-gra和标准剖面最高高度zref-sta为参考高度时，拟合不太理想. 提高测点的参考高度，利于提高预测精度.

(2)考虑零平面位移d的式(3)拟合精度最高，但限于d确定得较为主观且α与d的负相关性，不考虑d的式(1)在粗糙元非均质且测点众多的研究中更具实际意义. 理想d值的不确定对α的结果影响很大，不同测点对应着不同粗糙度的下垫面，d有很大差异性.

(3)采样厚度(廓线厚度)与α关系的理论探讨相对较少，研究发现α与底部廓线厚度呈一种收敛关系，且不同粗糙程度的下垫面的α基本稳定在0.25～1 H厚度段内上，而0.25～1 H也是本文推荐的理想采样厚度.

风洞测量结果的准确性依赖于下垫面三维模型刻画的精细程度和数据量测手段的改进，本实验建筑模型为500 m×500 m的网格概括，概括精度还有一定提升空间，数据获取仍为较为传统的皮托管定点量测，未来可通过红外三维扫描、增加测量截面范围和耦合热力边界等技术方法提高数据源的准确性. 风指数剖面模拟应重点关注具有物理属性的零平面位移d，实际上除了提高拟合精度，零平面位移d更代表了城市冠层下垫面发育风廓线的高度范围，零平面位移以上高度范围更容易发育指数风廓线，本文所发现的α与d的负相关性的物理数学涵义也更需着重解释. 由于3个模型尤其是1∶500模型的粗糙元形态较为复杂，且构建α与粗糙元密度、高度、迎风面密度等形态学参数关系的下垫面空间范围确定尚未达成共识，本文只分析参数选取对指数廓线α和拟合精度的影响，并未深入探讨α与下垫面粗糙元之间的联系机制，未来二者关系的探究可通过规定下垫面空间范围或尝试数值模拟等多样化方法来实现突破. 分析α沿风程方向的空间分异规律并确定风程序列上的增减速区分布，也是未来值得挖缺的研究内容. 因此，改进风洞试验测量技术条件，拓展指数α研究内容和领域，还需要进一步的努力探索.

[1] 丁国安,朱瑞兆. 关于低层大气风速廓线的讨论[J]. 气象,1982(8):18-20.

[2] TAHBAZ M. The estimation of the wind speed in urban areas[J]. International Journal of Ventilation,2009,8(1):75-84.

[3] LU L,SUN K. Wind power evaluation and utilization over a reference high-rise building in urban area[J]. Energy and Buildings,2014,68:339-350.

[4] BAILEY B H. Predicting vertical wind profiles as a function of time of the day and surface wind speed[C]//Proceedings of an international colloquium on wind energy. Brighton:BWEA,1981.

[5] WANG Z Y,PLATE E J,RAU M,et al. Scale effects in wind tunnel modelling[J]. Journal of Wind Engineering and Industrial Aerodynamics,1996,61(2):113-130.

[6] BANUELOS-RUEDAS F,ANGELES-CAMACHO C,RIOS-MARCUELLO S. Methodologies used in the extrapolation of wind speed data at different heights and its impact in the wind energy resource assessment in a region[M]. Vienna:INTECH Open Access Publisher,2011:97-114.

[7] ANSLEY R M,MELBOURNE W,VICKERY B J. Architectural aerodynamics[M]. London:Applied Science Publishers,1977:1-276.

[8] 申华羽,吴息. 近地层风能参数随高度分布的推算方法研究[J]. 气象,2009,35(7):55-60.

SHEN H Y,WU X. Research on algorithm of wind energy parameters in surface layer with height[J]. Meteorological Monthly,2009,35(7):55-60.

[9] 方平治,赵兵科,鲁小琴,等. 台风影响下福州地区的风廓线特征[J]. 自然灾害学报,2013,22(2):92-97.

FANG P Z,ZHAO B K,LU X Q,et al. Study on characteristics of wind profiles affected by landed typhoons in Fuzhou area[J]. Journal of Natural Disasters,2013,22(2):92-97.

[10] COUNEHAN J. Wind tunnel determination of the roughness length as a function of the fetch and the roughness density of three-dimensional roughness elements[J]. Atmospheric Environment,1971,5(8):637-642.

[11] PENWARDEN A D,WISE A F E. Wind environment around buildings[R]. London:Her Majesty’s Stationary 0ffice,1975．

[12] 黄鹏,全涌,顾明. TJ—2 风洞大气边界层被动模拟方法的研究[J]. 同济大学学报(自然科学版),1999,27(2):136-140；144.

HUANG P,QUAN Y,GU M. Research of passive simulation method of atmospheric boundary layer in TJ -2 wind tunnel[J]. Journal of Tongji University,1999,27(2):136-140；144.

[13] ISHIHARA T,HIBI K,OIKAWA S. A wind tunnel study of turbulent flow over a three-dimensional steep hill[J]. Journal of Wind Engineering and Industrial Aerodyna-mics,1999,83(1):95-107.

[14] 徐洪涛,廖海黎,李明水,等. 利用尖劈和粗糙元技术模拟大气边界层的研究[J]. 公路交通科技,2009,26(9):76-79.

XU H T,LIAO H L,LI M S,et al. Simulation of atmosphere boundary layer by using wedge and roughness element technique[J]. Journal of Highway and Transportation Research and Development,2009,26(9):76-79.

[15] KARLSSON S. The applicability of wind profile formulas to an urban-rural interface site[J]. Boundary-Layer Meteorology,1986,34(4):333-355.

[16] KAWATANI T,CERMAK J E. Characteristics of the mean flow over a simulated urban area[C]//Proceedings of the Third International Conference on Wind Effects on Buildings and Structures. Tokyo：[s.n.],1971.

[17] 李秋胜,郅伦海. 沙尘暴天气下城市中心边界层风剖面观测及分析[J]. 土木工程学报,2009,42(12):83-90.

LI Q S,ZHI L H. Observation of wind profile and analysis of atmosphere boundary layer in urban areas[J]. China Civil Engineering Journal,2009,42(12):83-90.

[18] MACDONALD R W,GRIFFITHS R F,HALL D J. A comparison of results from scaled field and wind tunnel modelling of dispersion in arrays of obstacles[J]. Atmospheric Environment,1998,32(22):3845-3862.

[19] AHMAD K,KHARE M,CHAUDHRY K K. Model vehicle movement system in wind tunnels for exhaust dispersion studies under various urban street configurations[J]. Journal of Wind Engineering and Industrial Aerodyna-mics,2002,90(9):1051-1064.

[20] HSU S A,MEINDL E A,GILHOUSEN D B. Determining the power-law wind-profile exponent under near-neutral stability conditions at sea[J]. Journal of Applied Meteoro-logy,1994,33(6):757-765.

[21] BERNEISER A,KÖNIG G. Full scale measurements of wind velocity on different high-rise buildings in Frankfurt /Main[C]//Leipzig Annual Civil Engineering Report. Leipzig:Institut für Massivbau und Baustofftechnologoe,1996:303-318.

[22] FARELL C,IYENGAR A K S. Experiments on the wind tunnel simulation of atmospheric boundary layers[J]. Journal of Wind Engineering and Industrial Aerodyna-mics,1999,79(1):11-35.

[23] 纪芸,孙武,李国,等. 1907～1968年广州建成区土地利用/覆被变化时空特征分析[J]. 华南师范大学学报(自然科学版),2009(1):121-126.

JI Y,SUN W,LI G,et al. Space-time features analysis of land use/cover change in Guangzhou urban built-up area from 1907-1968[J]. Journal of South China Normal University (Natural Science Edition),2009(1):121-126.

[24] DAVENPORT A G. Rationale for determining design wind velocities[J]. ASCE Journal of the Structural Division,1960,86(5):39-68.

[25] JACKSON P S. On the displacement height in the logarithmic velocity profile[J]. Journal of Fluid Mechanics,1981,111:15-25.

[26] 李会知,樊友景,庞涛,等. 在4m×3m风洞中模拟大气边界层[J]. 郑州大学学报(工学版),2003,24(4):90-92.

LI H Z,FAN Y J,PANG T,et al. Atmospheric boundary layer simulation in 4m×3m aeronautical wind tunnel[J]. Journal of Zhengzhou University(Engineering Science),2003,24(4):90-92.

Influence of Exponential Parameters Selection on Exponent and Profiles Precision

QI Honggang1, SUN Wu1*, LI Qingxiang2, HUANG Qiming2, HUANG Sheng1, JIANG Yunfeng1, LIANG Xingyi1

(1. School of Geography, South China Normal University, Guangzhou 510631, China;2. The Wind Engineering Research Center of Guangdong Provincial Academy of Building Research, Guangzhou 510500, China)

Based on the 3D model of Guangzhou main built-up area at 1∶7 000 horizontal scale, 1∶500,1∶1 000,1∶2 000 vertical scale respectively, a wind tunnel simulation is carried out on the neutral flow of B atmospheric boundary layer. With wind velocities in more than 26 test points,15 heights of each prevailed wind of the northwest and southeast, the uncertainties generated by reference heightzref, zero-plane displacement heightdand sample thicknesstto exponentαand fitting precision are all discussed, which provide some guidance to raise fitting precision on power law applications later. It is found that a reference height equal to maximum height of test points has a relatively smaller mean value and dispersion ofα, and a better fitting precision than otherzref;dcan improve fitting precision and is correlated withαnegatively. The exponential law of d in the zero plane displacement is not considered; it is more practical especially for the researches of inhomogeneous terrain and numerous test points. In differently rough terrain,αconverges at 0.25～1 H of the thickness of wind profiles and 0.25～1 H is the ideal sampling thickness.

2016-04-01 《华南师范大学学报(自然科学版)》网址：http://journal.scnu.edu.cn/n

国家自然科学基金项目(41771001);广州市科技计划项目(201704020136)

*通讯作者:孙武，教授，Email:sunwu@scnu.edu.cn.

K903

A

1000-5463(2017)05-0072-07

【中文责编：庄晓琼 英文审校：肖菁】