心理学可重复性危机两种根源的评估

骆大森

(美国宾夕法尼亚印第安纳大学，美国)

心理学可重复性危机两种根源的评估

骆大森

(美国宾夕法尼亚印第安纳大学，美国)

心理学的可重复性危机有两大已知的根源：传统统计学中虚无假设显著性检验体系的局限，和心理学的学术传统中的弊端，本文以开放科学协作组2015年报告的数据为依据，试对这两个根源的影响作一粗略的估算。采用Goodman（1992）和Cumming（2008）提出的方法对传统统计体系所加诸于可重复性的限制加以分析后，估算的结果表明传统统计学体系的制约，虽然有举足轻重的影响，却远不能完全解释该报告中低至36%的可重复率，该报告所反映的状况，显然还另有重大的非统计学的根源。本文进一步用Ioannidis（2005）提出的模型对这类非统计学因素的影响加以分析。分析后得到的若干组人为偏差率和Ha真实概率的估算，表明在原来研究所获得的几乎清一色的阳性结果中，大约只有不到三分之一或更低的比例是真阳性，而且相当部分的阳性结果，可能由人为偏差所造成。这样的分析可比较具体地描述该类因素对当前可重复性危机的可能影响。

心理学可重复性危机，传统统计检验的局限，心理学学术传统中的弊端，备择假设真实概率，人为偏差，危机根源的评估。

1 引言

近期来一些大规模调查的结果，使心理科学研究的可重复性成了人们议论的焦点，这些议论，不但见诸于影响因子最高的科学期刊上（Open Science Collaboration, 2015; Baker, 2015, 2016;Gilbert, King, Pettigrew, & Wilson, 2016; Anderson et al., 2016），也出现在享有很高声誉的大众媒体上（如Carroll, 2017），在中国国内的心理学同行中，也引起了相当的关注（胡传鹏等, 2016; 焦璨,张敏强, 2014; 朱滢, 2016）。特别值得注意的是，这一问题并不仅仅困扰着心理学科学工作者，也在其它重要科学领域中掀起不小的波澜。比如最近经过严格验证发现，在五篇有影响的癌症研究文章中，只有两篇的结果被重复验证所肯定（Kaiser, 2017），引起了生物医学界中的一场轩然大波。这一系列的情况，使得当前对科学研究可重复性的反思，在一个前所未有的深度和广度上展开，而积极关注和参与这一反思，是广大心理工作者，包括中国心理工作者无可推脱的职责。

若干年来，人们对心理学研究的可重复性一直存在着种种疑问，这些疑问中，最引人关切的是心理学在研究的可重复性上是否存在着可称作危机的严重问题。虽然对于危机与否的确定，难免受各人主观成见的影响，但最近的发展，至少使得人们对问题的严重性有了比较清醒的认识。本文采用危机的提法，主要为了强调解决这一问题的紧迫性，如听任流弊相沿，不全面改变心理学研究的现状，其后果对心理科学的发展可能是灾难性的。当前的分歧其实主要是如何对危机的严重程度作一个客观的评价，例如不少人并不认为局面已经到了令人十分悲观的地步，觉得目前的一些严厉评批有言过其实之虞（Gilbert et al.,2016）。对这一危机的严重程度作一恰如其分的估价，难度颇大，但有一定的必要性，因为做出一个较准确的估价，将帮助人们提出更有效更有针对性的措施。

正像不少人在讨论中所指出的那样，当前的可重复性危机，既有学术传统上的根源，也有统计学上的根源（Goodman, 1992; Cumming, 2008;Ioannidis, 2005, 2012; John, Loewenstein, & Prelec,2012; Joober, Schmitz, Annable, & Boksa, 2012; Nosek,Spies, & Motyl, 2012; Wagenmakers, Wetzels,Borsboom, van de Maas, & Kievit, 2012; 胡传鹏等,2016; 焦璨, 张敏强, 2014），而从这两个根源各作一些分析，得出某种虽然粗略但合理的估价，可帮助人们在对这一危机的反思中较好地把握分寸。本文拟以尽可能浅显的方式，提供一点这样的分析，期能对广大心理学者的反思有所助益。

2 对现状的调查

2015年，以开放科学协作组名义发表的一份报告（OpenScience Collaboration，下文简称OSC，2015），在已经议论丛生的心理学界引起了巨大地反响。OSC选取了2008年在三家心理学重要期刊上发表的100个研究结果，对每个选取的结果在新的被试样本中按原研究程序作了重复观察，并将重复的结果与原来的结果加以比较。经过比较，OSC的总的结论是：原来的结果只有一小部分经过重复得到验证。例如在原来的100个结果中，有百分之九十七达到了0.05水平上的统计显著性，而在重复观察的结果中，只有百分之三十六达到了0.05水平上的统计显著性。原来结果的平均实验效应值（mean effect size）为0.403（SD=0.188），而重复研究的平均实验效应值仅为0.197（SD=0.257）。只有47%的原来结果的效应量（effect size）落入重复研究的95%置信区间（confidence interval），也即意味有一半以上（53%）的原结果在统计上显著不同于重复结果。OSC认为如此不尽人意的可重复性，反映出心理学在学术传统上过于强调研究成果的创新意义，而过于轻视研究成果的可重复性。

OSC的一些主要成员此前还进行过另一个有关心理学研究可重复性的协作项目（Klein et al.,2014, 以下简称Many Labs，2014），该项目的重点是调查心理学以往一些研究的效应量的可重复性，及几个可能影响其可重复性的因素。该项目选取了13项以往发表的结果，由参加该协作的每家研究机构（共36家）对其中每项结果均做重复实验，从而可提供每项选取结果的三十多个重复研究结果。在选取的结果中，有些是著名的实验成果（如若贝尔奖得主Kahneman的两个经典的成果），也有些是比较近期发表的成果。有些成果已知有优良的可重复性，有些成果的可重复性则尚待验证。最终的数据显示：在13项结果中，有10项的统计显著性被重复实验所证实。但这些显著性被证实的结果，它们的效应量多和重复实验的效应量不相吻合，例如仅有百分之三十强的重复实验的效应量中值落入了原来效应量的95%置信区间（confidence interval）中，其它的重复实验的效应量中值都较远地偏离了原效应量。

Many Labs研究组最近又完成了另一项由二十家机构协作的重复性研究（Ebersolea et al., 2016; 以下简称Many Labs 2016）。这次在选取重复对象时，该研究组避开了公认的具有优良可重复性的对象，仅选取社会心理学和人格心理学领域里可重复性性质不明的一些研究成果作为重复的对象，最后选中的九项都属于比较引人注意但在可重复性上存在某些疑问的研究成果。这二十家机构对九项中的每项结果都进行了重复研究，从而取得了每项结果的二十个重复样本。这些重复样本的数据在统计显著性上只验证了原来九个结果中的三个，而且其中有一个的原效应量与重复结果的效应量相去较远。

科学讲究严密，而这些报告所反映的状况，难免令人对心理科学的严密性打一个不小的问号。如上文所述，如果人们将关注的眼光，延展到超越心理学疆界的更广大的科研领域中去，就会发现在研究可重复性方面存在的问题，有着更为普遍深远的根源，而这些根源，既有统计学上的，又有非统计学的学术传统上的，亟待人们追本寻源，逐一厘清。本文拟以OSC（2015）的报告为样本，对这两大类根源作一区分，并分别提供对于二者的粗略估价。

3 传统虚无假设显著性检验体系对可重复性的制约

3.1 制约的根源

传统虚无假设显著性检验（null hypothesis significance testing, NHST）体系中最关键的部分，第一是提出所谓的虚无假设（null hypothesis,H0），第二是根据现有的数据对H0做出保留或拒斥的二元决策。更具体来说，虚无假设可表达为H0=0，或效应量为0，而如果拒斥H0, 则接受H0≠0（也可以是＞0或＜0）的备择假设（alternative hypothesis, Ha）。从现有数据中所获得的统计量如果达到事先预定的显著性标准，则拒斥H0=0并接受Ha, 否则便保留H0=0的虚无假设。这一二元决策的任一结果，都会有错误的可能，即一类错误（type 1 error）和二类错误（type 2 error）。一类错误指真实效应量（true effect size）等于0时（H0=0）统计检验却呈显著的错误，而二类错误则指真实效应量不等于0（或大于/小于0）时统计检验却呈不显著的错误。

举例来说，如果有人要比较男女儿童在智商上可能的差异，他/她首先必须阐述H0，也即首先假定男女儿童在智商上的差异为0（效应量=0，或H0=0）。假设检验的结果，如果是拒斥了H0，则意味着必须接受Ha，认为男女儿童有智商差异。由于假设检验是一种统计的检验，检验的结论都会有或大或小的错误概率。如果最终的决定是拒斥虚无假设（拒斥男女儿童智商差异为0的假设），而实际上虚无假设倒是正确的（男女儿童在智商上差异确实为0），则结论的错误属一类错误。倒过来，如结论是肯定男女儿童智商差异差异为0这一H0假设，而Ha却偏是对的，亦即男女儿童的智商差异实际并不为0，则结论的错误属二类错误。

在拒斥虚无假设时，须预先划定一类错误概率的容忍范围，一般该范围选择在0.05（或0.01）以下。如果从现有数据获得的统计量在一类错误水平上低于0.05或0.01，通常的说法就是研究的结果在统计上显著，也即认为这样小的一类错误可以容忍，因而拒斥H0=0，接受Ha。对于这样的结果有一种误解，是认为既然现有的数据表明H0=0（真实效应量=0）成立的概率低于0.05，那么Ha（H0≠0，或真实效应量≠0，即例子中所述的男女儿童的真实智商差异不为0）成立的概率应大于0.95，也即误以为在重复研究时发现男女儿童智商有显著差异的概率应大于0.95，但实际上，这个概率会远小于0.95。

Goodman（1992）指出，比较理想的情况下，当真实效应量等于原来研究所报告的效应量时，原来0.05水平的显著成果，只有约0.50的概率在重复时也呈0.05水平上的显著，原来0.01水平的显著成果，只有约0.73的概率在0.05水平上呈显著（见图1）。

图1a取之Goodman（1992, Figure 1），但做了改动。原图中首次检验的统计值的显著水平由0.01改为0.05。图1b也据Goodman（1992, Figure 1）做了部分改动。对于双向（2-tailed）检验，Ha的分布曲线在左侧尚有小于–zα/2=–1.96的竖条阴影部分，在图1a和图1b中该阴影部分因太微小而无法显示。

Goodman以简单的z检验说明以上的结论，但同样的结论也适用于更复杂的t检验和F检验。仍以男女儿童智商差异为例，根据H0=0的假设，男女儿童的总体平均差别应等于0。在首次取样时，女童的样本平均（sample mean）比男童的样本平均高出3.0，且由该3.0的差异得出的检验统计量z=1.96正好位于双向（2-tailed）0.05水平显著的分界点上。假定事先拟定的一类错误水平是0.05，那么检验的结论就应是男女儿童在智商水平上有显著差异，从而拒斥H0=0。做出这一结论的依据是，如果H0=0成立的话，再在男女儿童总体中以同样的方式反复取样，将会有95%的男女样本平均差落在–3.0和3.0之间，而仅有5%的样本平均差会超出±3.0，如此微小的几率，使得H0=0难以成立，因此拒斥H0。但这样的结果并不意味着Ha成立的概率将大于或等于95%。

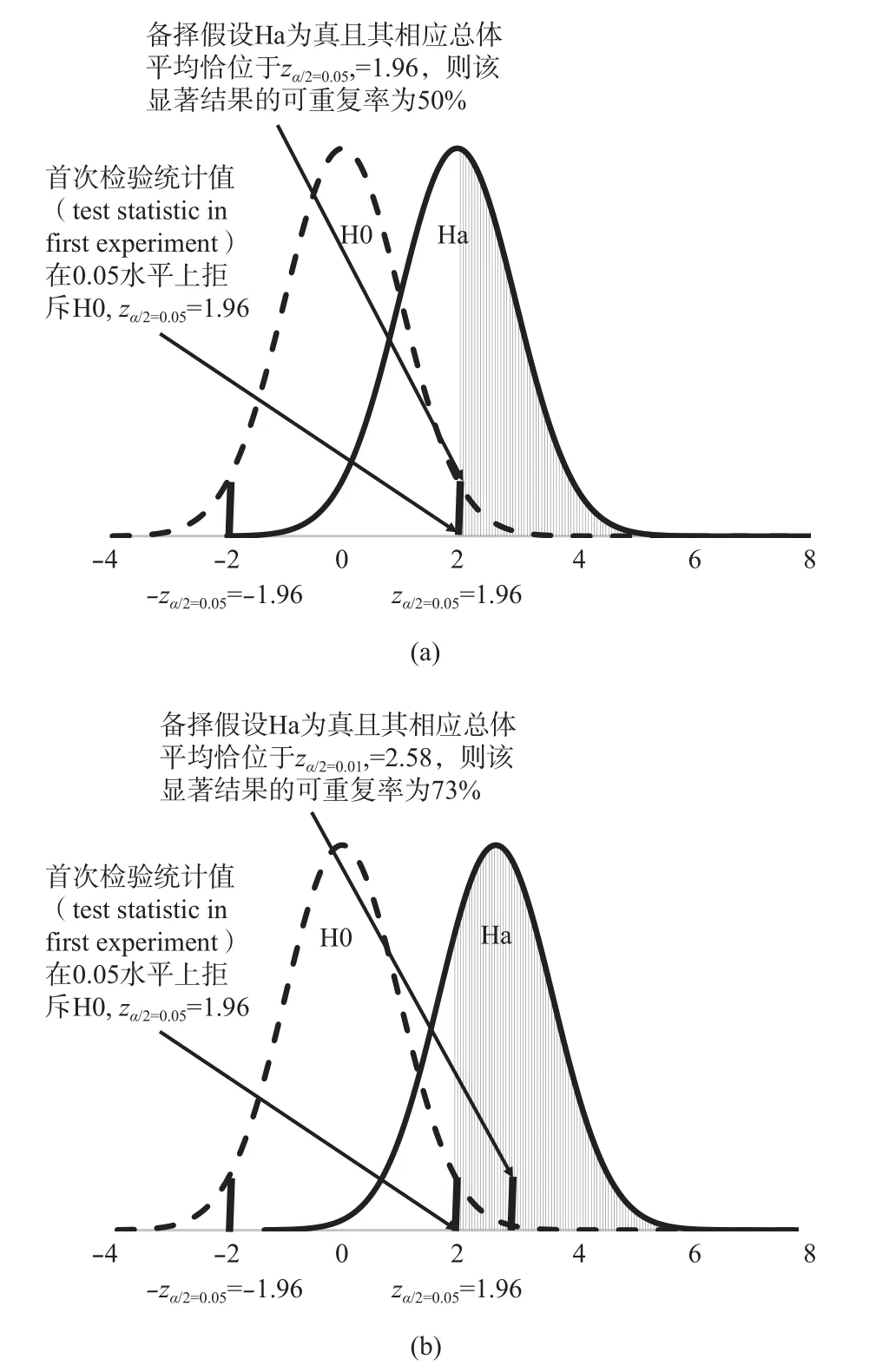
图 1 首次检验显著水平为0.05或0.01，假定真实效应量已知，重复验证时获0.05水平显著结果的概率分布

为了便于说明，先假定男女儿童智商的总体平均差异（population mean difference）确实不为0，且该差异恰好是3.0，也即Ha=3.0在儿童总体中成立。这样的情境，并不意味着在未来的研究中有95%的概率重复女童显著高于男童的结果，因为男女儿童的样本平均差（sample mean difference）是一个随机变量，在未来的研究中也会随机地在3.0上下浮动，实际女童的样本平均比男童的样本平均高3.0或更多的概率在未来的重复实验中仅有50%（见图1a）。

以上假设的情境会使人产生一个疑问：在实际的研究中，所获得的显著结果极少有可能正好落在0.05的临界点上，绝大部分的显著结果会是低于0.05的临界点，如果这样的话，显著结果的可重复性是否会大大提高了呢？图1b表明即使首次研究的结果明显地低于0.05的水平，而达到了0.01的水平，在未来的重复实验中，仍然只有73%的结果会在0.05水平上显著。以男女儿童智商差异为例，假如在首次实验中男女儿童的样本平均差是3.87，样本统计量z=2.58，显著水平为0.01。再假定男女儿童的总体平均差确为3.87，但由于男女儿童的样本平均差是一个随机变量，在重复取样时，仍会有27%的样本平均差会小于3.0而达不到0.05的显著水平。

以上Goodman（1992）所设想的这些情境都假定真实的效应量是已知的（如男女儿童智商的总体平均差异为已知的3.00或3.87），但在绝大多数的实际研究中，真实的效应量是无法确定的。Goodman指出，在真实的效应量未知的情境中，显著结果的可重复率将会更低。

Cumming（2008）进一步分析了真实的效应量未知的情况。如果真实的效应量未知（例如男女儿童智商的总体平均差异未知），已知的仅是在某次实验中样本平均差的显著水平，诸如0.030，0.008之类的低于0.05临界点的一类错误概率水平，人们仍可以据此推算以后在同类实验中得到显著结果的概率，只是由于有关真实的效应量的不确定性，显著结果的可重复率将会低于上述Goodman所列出的水平。图2是Cumming的分析的一个图解。该图据Cumming（2008, Figure A3）做了改动。原图中首次检验的统计值的显著水平由p获得=0.11改为p获得=0.01。对于双向（2-tailed）检验，Ha的分布曲线在左侧尚有小于–zα/2=–1.96的竖条阴影部分，但因其过于微小而无法显示。图中左面的钟型曲线代表了H0=0的分布，横轴上z=–1.96和z=1.96是双向0.05显著水平的临界点。假定某次实验中获得的结果是样本平均差的显著水平为0.01，由于该水平低于预先划定的0.05水平，实验的结论是拒斥H0=0，接受Ha。图中右面的曲线代表了获得0.01显著水平时Ha的分布，这一曲线并不假设真实的效应量已知，它所依据的只是获得的显著水平p获得=0.01。这个分布曲线的特点是它的方差要大于左面的曲线，反映出由于真实效应量未知所造成的更大的不确定性。如图所示，右面曲线覆盖下的右侧竖条阴影区域代表了在将来类似实验中可重复0.05水平显著结果的概率。这一概率是0.67，低于图1b中的0.73。

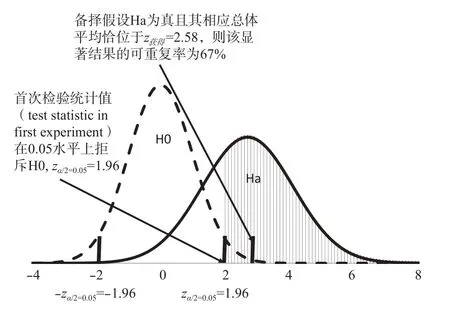
图 2 首次检验显著水平为0.01，假定真实效应量未知，重复验证时获0.05水平显著结果的概率分布

3.2 依据NHST的制约对心理学的可重复性危机作一估算

上述Goodman和Cumming的分析表明，传统H0=0的假设检验体系无形中为该体系中产生的成果的可重复性设置了一个上限，心理科学研究的可重复性也受这一无形上限的羁绊而难臻理想的水平。这样的分析同时也演示了合理的分析方法，可用来帮助估算心理学的可重复性危机的程度。

根据OSC（2015）的报告，在全部原来研究的0.05水平的显著结果中，有36%得到了重复验证。这些原报告的结果，可以在线获得（https://osf.io/5wup8） 。原报告的结果中列出了所选取的97个达到显著结果的统计量（F, t, z, χ2, r）以及有关的自由度（df）或样本量。根据这些信息可得到这些结果的显著性水平。为统一起见，所有的t，z和r的显著水平均根据双向（2-tailed）检验确定。这样得出的显著水平的中值（median）=0.0069，也即原结果的显著水平在0.0069上下。用Goodman和Cumming的分析方法，可进一步粗略估算OSC报告的研究的可重复率。这样估算的可重复率，代表了按照NHST体系严格操作，排除任何非统计学因素所应当得到的可重复率。图3a和图3b显示了原结果的显著水平在0.0069上下时，用Goodman和Cumming的分析方法所得出的可重复率。二图在原则上和图1b和图2一致，但图中首次检验的统计值的显著水平为OSC报告所得的显著水平的中值0.0069。对于双向（2-tailed）检验，Ha的分布曲线在左侧尚有小于–zα/2=–1.96的竖条阴影部分，但因其太过微小而无法在二图中显示。

按照Goodman（1992）的分析方法，假设真实效应量（true effect size）已知并等于原研究的效应量，从0.0069的显著水平可推算出0.77的可重复率（见图3a和附录A）。按照Cumming（2008）的分析方法，不假定真实效应量已知，当p获得=0.0069时，可推出可重复率为0.70（见图3b和附录A），二者均大大高于OSC报告的0.36的可重复率。这一比较的结果颇发人深省，这意味着统计学的NHST的制约，只是造成心理学可重复性危机的原因之一，另外还有不能归咎于统计学的重要因素。

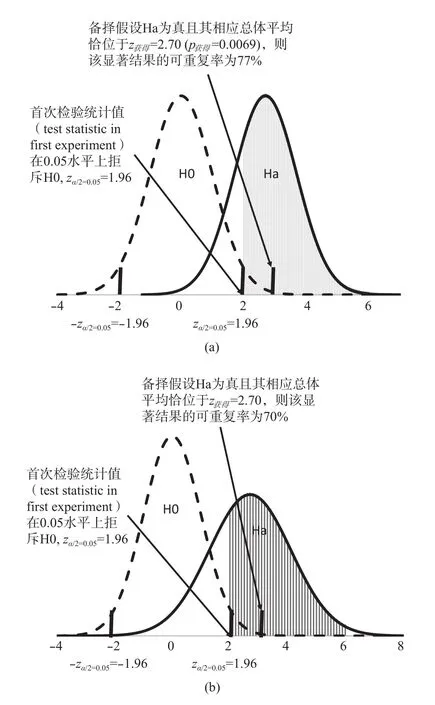
图 3 首次检验显著水平为0.0069，假定真实效应量未知或未知，重复验证时获0.05水平显著结果的概率分布

4 估测非统计学根源对重复性危机的影响

4.1 统计学和非统计学因素对可重复性的综合影响

Goodman和Cumming所分析的仍然是不受人为偏差干扰的规范操作，在现实世界里，自选题至发表结果的整个过程中，尚有种种偏离规范的人为因素，能进一步削弱研究的可重复性，且这些因素的影响可以逐步累加，最终导致结果的可重复性下降到科学上难以容忍的水平。

更具体地来说，Goodman和Cumming的分析方法，都依据于一个关键的假定，也即假定备择假设（Ha）为真，而将无法重复显著结果的根源全部归咎于二类错误，但实际研究的状况，往往与该假定大相径庭。首次实验时获统计显著的结果，导致接受备择假设（Ha），并不就意味着所接受的备择假设（Ha）就是真实的。而如果接受的备择假设（Ha）有不真实的可能，则结果的不可重复概率将可能大大高于二类错误。如以HTP代表备择假设（Ha）的真实性概率，以β代表二类错误概率，则备择假设（Ha）为真且得重复的概率是（1–β）HTP, 而不是研究强度（Power）=1–β。例如当HTP=0.5，β=0.30时，真实的备择假设（Ha）得到重复验证的概率是（1–0.30）×0.5 =0.35，而不是0.70。

当Ha真实概率（HTP）小于1.0时，还有所谓的假阳性的问题，也即虚假的备择假设因一类错误或其它的原因而呈显著（也即呈阳性）的可能，如以α代表一类错误概率，则因一类错误而呈假阳性的概率为α（1–HTP）。例如在OSC（2015）所报告的统计显著的原结果中，也许只有40%的备择假设为真，这样的话，在进行这一系列实验时，假阳性的概率就会是0.05×（1–0.40）=0.030。假阳性的概率并不仅受一类错误的影响，它的另一个影响因子是人为偏误（bias），诸如办公桌抽屉效应（desk drawer effect,也即只投送显著的结果以求发表, 而将不显著的结果留在办公桌抽屉里按下不表）, 发表偏见（publication bias，即只有显著的结果才得发表的机会），和可疑研究操作（questionable research practice）之类。如以μ代表人为偏误（bias）的总概率，则其对假阳性概率的影响可表达为μ（1–α）（1–HTP）。例如当一类错误（α）为0.05，Ha真实概率（HTP）为0.40时，虚无假设H0成立的概率是1–HTP =0.60, 避免一类错误的概率是1–0.05 =0.95，而如果人为偏差的概率是μ=0.30，那么由于人为偏差造成假阳性的概率是0.30×0.95×0.60=0.171。如以比较通俗的语言来解释这种情况，则可说在这一批研究中，尽管有60%的虚无假设（H0=0）是实际成立的，尽管一类错误（α）为0.05的临界值使得绝大部分（95%）H0=0分布总体中的样本不呈阳性（不呈统计显著性），但由于0.30的人为偏差率，使得这部分（0.95×0.60=0.57）本不应呈阳性的结果中有17.1%呈了阳性！

由于人为偏差是追逐阳性的倾向，它也可造成真阳性。当备择假设为真时，有部分结果因为二类错误而不呈阳性，这部分结果的概率是β×HTP，但由于人为的对于阳性的趋鹜，使得这些结果中的一些由阴转阳，其概率是μ×β×HTP。设二类错误β=0.30，Ha真实概率是HTP=0.50，人为偏差率μ=0.30，这一部分真阳性的概率则为0.30×0.30×0.40=0.036。

表1列出了以上诸项真假阳性概率。如用真阳性总概率除以真阳性总概率与假阳性总概率之和，就得到了所谓的阳性预测值（positive,predicted value, PPV），代表了在所有报告的阳性结果中真阳性的比例。

表 1 真阳性，假阳性和一类错误（α），二类错误（β），Ha真实概率（HTP），及人为偏差（μ）的关系

Ioannidis（2005）用统计模型对上述这类因素的影响作了系统分析。图4为Ioannidis模型的一个图解。该模型为：

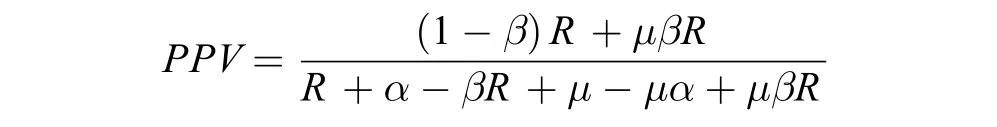
其中：

PPV=阳性预测值，

α=一类错误，

β=二类错误，

μ=人为偏差，

R=Ha真实概率/H0真实概率（在图中换算成Ha真实概率HTP=R/（1+R））。

Ioannidis的模型参数包括一类错误的概率（如以0.05或0.01作为显著性检验的标准），二类错误的可能水平（0.80, 0.60, 0.40, 0.20, 等等），某特定研究领域中所提出和检验的备择假设有多大的比例是真正成立的（例如在各种食品原料和配料中被怀疑为致癌物质中究竟有多大的比例是真实致癌的），以及研究过程中种种人为偏向的（如选择性报告结果，发表偏见，和可疑研究操作）总概率。Ioannidis发现，当下依赖传统统计方法的研究领域中，如果把典型的参数值范围（例如0.05的一类错误，0.40或更高的二类错误，低于0.10的Ha真实概率，0.10，0.20或更高的人为偏差概率）代入该模型，得出的结论是大部分的显著结果实际上并不真实。该模型还可进一步引出一些值得注意的结论，例如在一个探索性的领域中，Ha真实概率（HTP）往往很低，而如果Ha真实概率低于0.09（心理学的某些探索性领域是否能有超出这一水平的Ha真实概率，尚有待认真调查），即使研究的强度较高（例如低于0.20的二类错误），且无非常严重的人为偏差（如约为0.20的偏差概率），所报告的显著成果也仅有低于20%的真实率，使得人为偏差率竟超出了显著结果的真实概率，令人难免对研究结果的可靠性缺乏信心（见图4）。又譬如在一个很热门的领域中，有许多研究团队在追逐类似的显著性成果，而任何某团队所得到的显著性成果，就其自身而言，仅有很低的真实率。可以想见，在一个既热门又是探索性的领域中，显著性成果的真实率将会非常低，如果还存在较明显的人为偏差的话，则所报道的显著性成果的真实率，将低于人为偏差的概率。

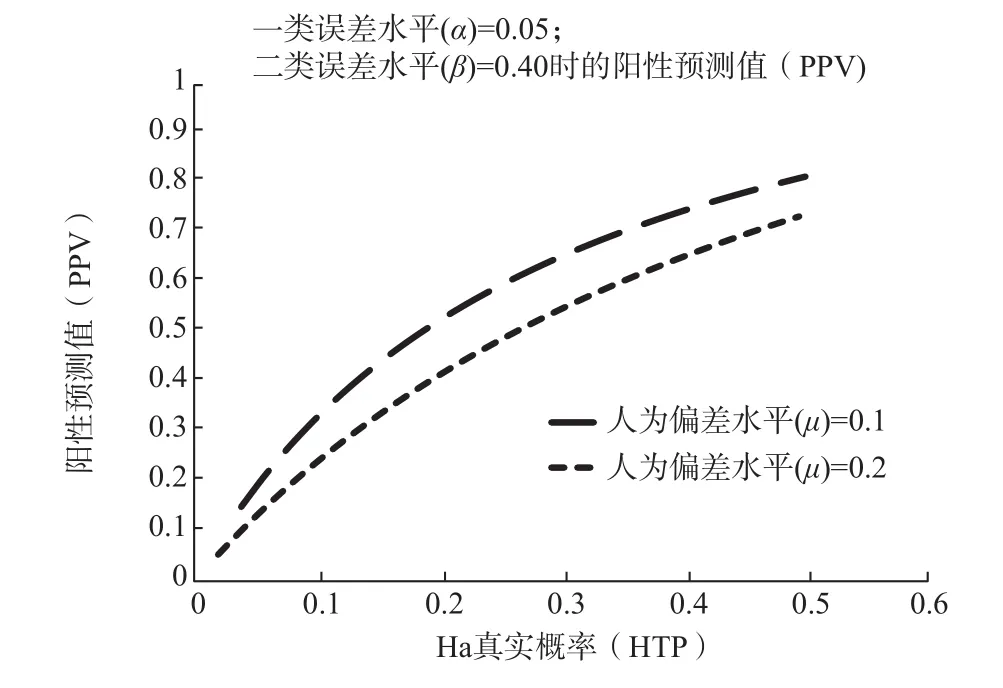
图 4 Ioannidis（2005）模型的图解

4.2 对影响心理学可重复性危机的非统计学因素的粗略估算

OSC和Many Labs所报告的研究结果的重复率在30%多的范围内。如以阳性预测值（positive predictive value，即阳性的报告结果实际上确为阳性的概率）作为研究结果得到重复验证的指标，这30%多的范围可作为阳性预测值的样本估算值（sample estimate）。这样的估算值，如代入Ioannidis（2005）的模型可用以推算心理学中人为偏差（bias, 以符号μ代表）和Ha真实概率（HTP）。图5显示了按照Ioannidis（2005）模型所作的推算。本图根据Ioannidis（2005）模型，先假定阳性预测值（PPV）已知，再将设定的一类错误值（α），二类错误值（β），和Ha真实概率HTP=R/（1+R）代入模型，求出人为偏差率（μ）的方程解。按照OSC（2015）的报告，已知阳性预测值（PPV）=0.36，一类错误（α）=0.0069, 取三个不同二类错误水平（0.30，0.40，0.50），分别在0.09到0.35的Ha真实概率（HTP）区间（也即0.10到0.54的R区间）内得出人为偏差率（μ）轨迹。轨迹方程见附录B。图中列出了三种可能的研究的二类错误水平：0.30（这在心理学中应算相当理想的水平），0.40（在心理学总体中仍然是很不错的水平）和0.50（可能是心理学研究总体的中上水平）。假设一类错误水平为OSC（2015）重复验证报告中採用的临界值0.05，则有一系列人为偏差概率（μ）和Ha真实概率（HTP）的组合值可令阳性预测值恰处OSC（2015）报告的36%的水平。

在OSC所选中的100个重复验证项目中，相对应的原研究均发表于心理学的一流期刊，从前文采用Goodman（2015）和Cumming（2008）方法分析的结果来看，大部分原研究至少在理论上都达到了二类错误（β）=0.30或研究强度（Power）=1 – 0.30 =0.70或更高的水平，故当一类错误值为0.05时，强度（Power）=0.70大体代表了这批研究的强度水平。设强度=0.70或二类错误β=0.30，在图5中可选取五种有代表性的Ha真实概率水平：HTP=0.33, HTP=0.25, HTP=0.20,HTP=0.15和HTP=0.09。在这五种水平中，HTP=0.33使得人为偏差率（μ）接近1.0的上限，未免太过极端。第五个水平HTP=0.09对应于Ioannidis所指出的Ha真实概率的下限，倘真反映了心理学的实际，则不免令人沮丧，但对应的μ=0.08左右的人为偏差概率显然低估了实际的人为偏差程度。HTP=0.25，HTP=0.20，和HTP=0.15这三个对应的组合可能更贴近实际一些。这三组估算值，分别对应于μ=0.48，μ=0.33，μ=0.20的人为偏差率，意味着在OSC所调查的原结果中，约有不到五分之一到将近一半的显著结果（包括假阳性和真阳性，但主要是假阳性）乃由非统计学的人为偏差因素（如选择性的报告和发表以及可疑研究操作）所造成，同时在原来研究所接受的全部备择假设（97个）中，可能仅有15%到25%为真。这几个组合所反映的状况，自然不免令人蹙额，但仍可说是好于最坏的估计。心理学总体的状况，可能会比OSC（2015）所报告的一流期刊上发表的结果更有不如。

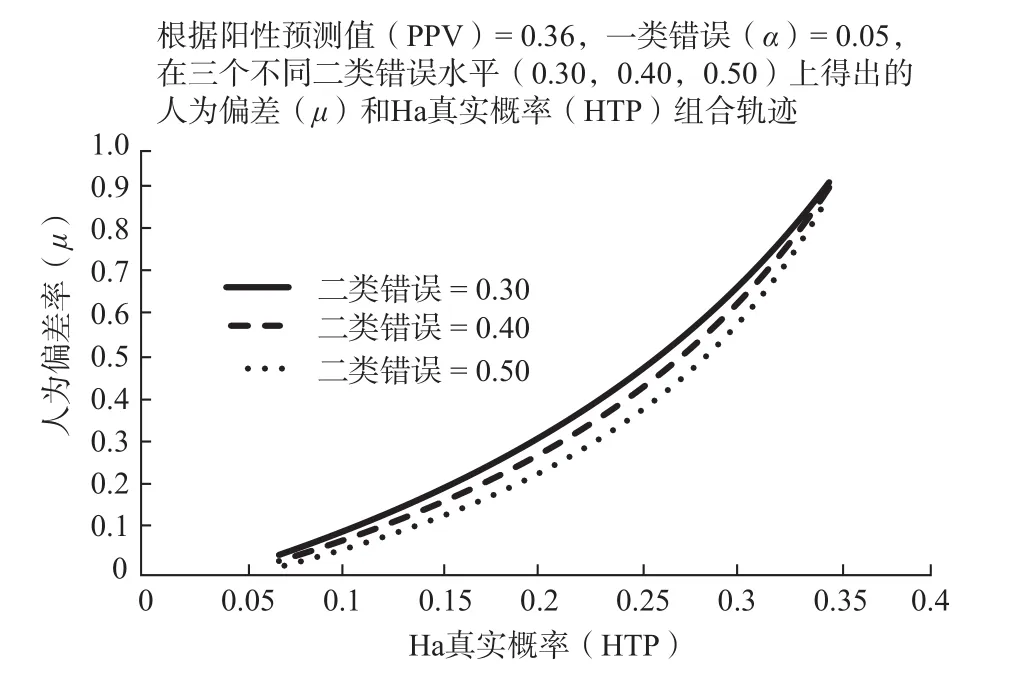
图 5 根据Ioannidis（2005）模型，已知阳性预测值（PPV） =0.36，一类错误（α）=0.0069，在三个二类错误水平水平上的Ha真实概率（HTP）和人为偏差率（μ）变化轨迹

从另一个角度来说，这样比较严重的非统计学的学术传统上的弊端，表明即使基于当前这个有缺陷的统计检验体系，心理学家们仍然是颇有可为的。在当前的体系中，如欲超越0.50的阳性预测值，心理学家们需要进一步以增大样本，选择研究较大的效应量等方式提高研究的强度，大力降低人为偏差，并在选题上更注重研究假设的真实性而不过于耽溺所谓的“创新探索”。例如在强度（Power）=0.80, 一类错误=0.05, 人为偏差μ=0.10,Ha真实概率HTP =0.15的水平上，阳性预测值可达0.50。如进一步降低一类错误标准到0.01，则阳性预测值可达0.58。倘再提高HTP到0.20的水平，可将阳性预测值增至0.65。这样的阳性预测率，如若再结合比NHST体系更有效的统计分析方法，可望使心理学研究的可重复性水平更上一个层次。

5 结语

本文以OSC（2015）报告的结果为依据，采用Goodman（1992）, Cumming（2008）, 和Ioannidis（2005）提出的分析方法，分别对传统NHST统计体系加诸于研究的可重复性的影响和心理科学中非统计学因素造成的有关困扰作了尝试性的定量评估。这样的评估当然有其局限。首先，OSC（2015）的结果只是一个不太大的样本。其次，某个研究未能通过该调查的重复检验，并不必然意味着这个研究的结果就是所谓的假阳性，而被该调查所支持的那些研究结果，也不一定就都是真阳性的结果，本文中将OSC（2015）所报告的36%的重复率作为所有阳性结果中真阳性的比例（PPV），只是一种粗略的样本估算。这些分析方法所基于的假设，也都难免对现实世界做了一些也许是过分的简化，由此而得的分析结果，至多只能算是某种大体的评估，不能替代进一步的大规模的如OSC（2015）和Many Labs（2014, 2016）一类的调查研究。但这些粗略的评估，仍可能帮助人们进一步认识心理学所面对的可重复性危机。

传统H0=0的假设检验体系无形中使研究成果的高度可重复性成了一个难以企及的目标，这一统计学上的制约是心理科学研究的可重复性危机的一个重要肇因。虽然统计学界已经在开始重估传统H0=0的假设检验体系，一个全新体系的形成，仍需时日，这对统计学的教育改革造成了不小的困难，但认真总结传统统计教育中的问题，并引用一些难度并不太高的方法和技术，如强调对结果的置信区间（confidence interval）的分析, 可以在一定程度上克服传统体系的障碍（Cumming，2008; 胡竹菁, 董圣鸿, 张阔, 2013），心理学家们应尽快地调整自己的知识结构以适应这样的变化。

从心理学家本身来说，长期以来对学科中种种忽视研究可重复性的做法，常采取一种视而不见的态度，也是一个难以否认的事实。这种长期的忽视，造成了学术传统上的种种流弊，其后果正如本文的评估所显示的那样，严重地损害了心理学的科学性。本文的分析也显示，如果鼎力革除这些弊端，即使在传统的统计学体系中，也可望长足地提高心理学研究的可重复性。

胡传鹏, 王非, 过继成思, 宋梦迪, 隋洁, 彭凯平.(2016). 心理学研究中的可重复性问题: 从危机到契机. 心理科学进展, 24(9), 1504–1518.

胡竹菁, 董圣鸿, 张阔.(2013). 《心理统计学》教学内容的新探索. 心理学探新, 33(5), 402–408.

焦璨, 张敏强.(2014). 迷失的边界: 心理学虚无假设检验方法探究. 中国社会科学, (2), 148–163.

朱滢.(2016). “开放科学 数据共享 软件共享”, 你准备好了吗?. 心理科学进展, 24(6), 995–996.

Anderson, C. J., Bahník, Š., Barnett-Cowan, M., Bosco, F. A., Chandler, J.,Chartier, C. R., …, Zuni, K.(2016). Response to comment on“Estimating the reproducibility of psychological science.”. Science,351, 1037.

Baker, M. (2015). Over half of psychology studies fail reproducibility test.Nature. http://dx.doi.org/10.1038/nature.2015.182.

Baker, M. (2016). Psychology’s reproducibility problem is exaggerated –say psychologists. Nature. http://dx.doi.org/10.1038/nature.2016.19498.

Carroll, A. E. (2017, May). Science needs a solution for the temptation of positive results. The New York Times. Retrieved from http://www.nytimes.com/.

Cumming, G.(2008). Replication and p intervals: P values predict the future only vaguely, but confidence intervals do much better. Perspectives on Psychological Science, 3(4), 286–300.

Ebersole, C. R., Atherton, O. E., Belanger, A. L., Skulborstad, H. M., Allen,J. M., Banks, J. B., …, Nosek, B. A.(2016). Many Labs 3: Evaluating participant pool quality across the academic semester via replication.Journal of Experimental Social Psychology, 67, 68–82.

Gilbert, D. T., King, G., Pettigrew, S., & Wilson, T. D.(2016). Comment on“Estimating the reproducibility of psychological science ”. Science,351, 1037.

Goodman, S. N.(1992). A comment on replication, P-values and evidence.Statistics in Medicine, 11(7), 875–879.

Ioannidis, J. P. A.(2005). Why most published research findings are false.PLoS Medicine, 2, e124.

Ioannidis, J. P. A.(2012). Why science is not necessarily self-correcting.Perspectives on Psychological Science, 7, 645–654.

John, L. K., Loewenstein, G., & Prelec, D.(2012). Measuring the prevalence of questionable research practices with incentives for truth telling.Psychological Science, 23(5), 524–532.

Joober, R., Schmitz, N., Annable, L., & Boksa, P.(2012). Publication bias:What are the challenges and can they be overcome?. Journal of Psychiatry & Neuroscience, 37(3), 149–152.

Kaiser, J.(2017). Rigorous replication effort succeeds for just two of five cancer papers. Science, , doi: 10.1126/science.aal0628.

Klein, R. A., Ratliff, K. A., Vianello, M., Adams, R. B., Jr., Bahník, Š.,Bernstein, M. J., …, Nosek, B. A.(2014). Investigating variation in replicability: A “many labs” replication project. Social Psychology, 45,142–152.

Nosek, B. A., Spies, J. R., & Motyl, M.(2012). Scientific utopia: II.Restructuring incentives and practices to promote truth over publishability. Perspectives on Psychological Science, 7, 615–631.

Open Science Collaboration.(2015). Estimating the reproducibility of psychological science. Science, 349, aac4716.

Wagenmakers, E. J., Wetzels, R., Borsboom, D., van der Maas, H. L. J., &Kievit, R. A.(2012). An agenda for purely confirmatory research.Perspectives on Psychological Science, 7(6), 632–638.

附录A

图3a所说明的是总体效应量已知情况下的可重复率。设φ（z）为标准常态累计分布函数方程（cumulative distribution function of the standard normal distribution），在图3a中，右侧竖条阴影部分和左侧竖条阴影因太微小而无法呈示的总面积为P = 1–φ（z+zα/2）+ φ（z–zα/2），此面积即重复验证时结果仍然显著的概率。其中zα指首次检验时显著性的临界值，如在双向（2-tailed）检验时z0.05/2= 1.96，z是首次检验时实际获得的z统计量。用Microsoft Excel函数可表达为：

P=1–NORMSDIST（z+NORMSINV（α/2））+NORMSDIST（z-NORMSINV（α/2）。

例如当首次检验时显著水平是0.0069，可得z=NORMSINV（1–0.0069/2）=2.7016, P=1–NORMSDIST（2.7016+1.96）+NORMSDIST（2.7016–1.96）=0.7709。

图3b说明的是总体效应量未知时的可重复率。和图3a不同的是，图3b右面的代表Ha的钟形曲线有较大的方差（2倍于左面代表H0的曲线的方差，也即约1.414倍于左面曲线的标准差）。在图3b中，重复验证时结果仍然显著的概率是P=1–φ（（z获得+zα/2）/√2）+ φ（（z获得–zα/2）/√2）。其中z获得指在首次检验时所获得的z统计量，可从首次验证时的显著水平p获得得出。该方程的Microsoft Excel函数表达为：

P=1–NORMSDIST（（z获得+NORMSINV（α/2））×SQRT（2）+NORMSDIST（z获得–NORMSINV（α/2））×SQRT（2））。

例如当首次检验时α/2 = 0.025，实际获得显著水平是p获得= 0.0069，可得z获得=NORMSINV（1–0.0069/2）=2.7016, P=1–NORMSDIST（2.7016+NORMSINV（α/2））×SQRT（2）+NORMSDIST（2.7016-NORMSINV（α/2））×SQRT（2））=0.7005。

附录B

根据Ioannidis（2005）的模型：

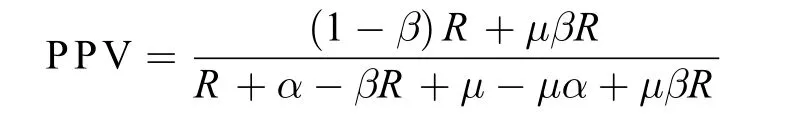
经过代数的换项整理可得人为偏差率（μ）的方程如下：

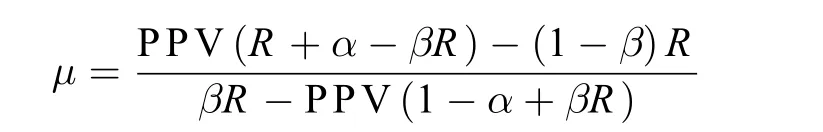
例如PPV = 0.36, α = 0.05, 设β = 0.30, HTP取其区间下限HTP = 0.09也即R = 0.10，将这些数值代入该方程得人为偏差率：

μ =（0.36×（0.10 + 0.05 – 0.30×0.10）–（1 – 0.30） × 0.10）/（0.30×0.10 – 0.36× （1 – 0.05 +0.30×0.10 ））= 0.08。

A Crude Evaluation on the Two Roots of the Reproducibility Crisis in Psychology

LUO Dasen
(Indiana University of Pennsylvania, USA)

The reproducibility crisis in psychology is known to have two roots, the root in the traditional statistical system of null hypothesis significance testing, and that in the academic tradition of psychology. This article was an attempt to crudely estimate the respective impacts of the two roots on the reproducibility crisis in psychology. The results reported by Open Science Collaboration(2015) were analyzed using the methods suggested by Goodman (1992) and by Cumming (2008) to roughly estimate the limiting influence on reproducibility imposed by the traditional system of statistics. The estimated limiting influence, although quite notable,appears to be far short of being able to account for the reproducibility rate as low as 36% indicated by the report, suggesting that factors other than the traditional system of statistics have played a tremendous role in the crisis. The model proposed by Ioannidis(2005) was adopted to analyze the possible impacts of factors other than the traditional system of statistics, and possible ranges of the joint impact of bias and the probability of true alternative hypotheses were extrapolated。 The analysis led to estimates indicating that, of all original positive results, only no more than one third, and probably even less, was true positive, and a considerable portion of these positive results was caused by bias. These results may help explicate how these factors are likely to contribute to the current crisis.

the reproducibility crisis in psychology, limitations of traditional system of statistical testing, flaws in the academic tradition of psychology, the probability of true alternative hypotheses, bias, evaluation on the roots of the reproducibility crisis.

B841

2017–8–10

骆大森，E-mail: dluo@iup.edu。