出租车载客热点精细提取的改进DBSCAN算法
江慧娟,余 洋
(1.武汉大学 遥感信息工程学院,湖北 武汉 430079)
出租车载客热点精细提取的改进DBSCAN算法
江慧娟1*,余 洋1
(1.武汉大学 遥感信息工程学院,湖北 武汉 430079)

随着城市化水平的提高和居民公共交通出行的需求增长,要求有更精细化的聚类方法提取出租车载客的热点区域。针对基于密度聚类在出租车数据聚类中存在的问题,设计一种基于路网约束的改进DBSCAN算法。该算法通过将行程距离引入DBSCAN算法中,改进原有DBSCAN算法在出租车数据聚类中存在的精细尺度聚类参数选择和设置困难问题,弥补现有聚类算法在出租车载客热点区域提取方面的不足。利用武汉市出租车GPS轨迹数据进行的实验结果表明,在加入道路约束后,算法在出租车载客热点区域的精确提取方面具有较好的效果。
载客热点;密度聚类; DBSCAN算法;路网约束;出租车数据
当前研究中,基于出租车数据进行载客热点的提取主要包括两种方法[1,2]:一种是通过划分统计单元的方式,将研究空间划分为有限数目的单元以形成网格结构,然后统计每个网格中载客点的数量,对载客数量超过阈值的网格按照空间邻近进行合并,从而形成大小不同的相似特征区域,实现热点区域的提取[3-5]。另一种方式采用无监督聚类方式“自下而上”地发现出租车载客点的聚集情况[6-8],通过遍历一定时间内的所有载客点,在计算载客点之间距离的基础上,通过设置点的数量阈值和搜索半径,计算点所在区域的密度,进而得到聚类,形成聚类热点区域[9-11]。但这两种方法都有一定的局限性。
本文提出一种顾及路网约束的改进DBSCAN算法(Road Limitation DBSCAN,简称RL-DBSCAN),该算法针对现有算法在出租车载客热点区域提取结果的不足,将道路拓扑关系、路段长度信息作为约束条件加入聚类算法的相似性度量中,并利用武汉市出租车GPS轨迹数据进行了实验。实验结果表明,RLDBSCAN算法对出租车载客热点区域的精确提取方面具有较好的效果,可为细粒度的城市载客热点提取、居民出行时空特征分析、辅助居民生活进行智慧行为决策提供更精准的信息支持。
1 基于路网约束的改进DBSCAN算法
1.1 基于DBSCAN算法的载客热点提取
DBSCAN算法是基于密度聚类算法中的一种简单有效且比较典型的算法。算法主要通过调整Eps和MinPts两个参数进行热点和热度的提取。由于这些出租车载客点一般沿道路分布,所以聚类结果容易产生条带状的类簇,而一般方法均以簇的质心作为载客热点,这样就容易导致所提取的载客热点难以准确反映实际的乘车热点位置。如图1所示,用不同的颜色表示聚类形成的类簇,可以发现红色载客点形成的类簇,能反映这条道路上的乘车热度较大,由于道路较长,若以这一类簇的质心作为热点,则难以真实反映这条道路上不同地段的热点聚类情况。

图1 DBSCAN算法形成的载客聚类结果
分析DBSCAN算法的基本原理,可以发现由于该算法主要只考虑了载客点之间的距离和每个类簇包含的点数目,因此,算法容易将处于道路交叉点(图2a)或同一路段不同方向的载客点聚为一类(图2b)。

图2 DBSCAN算法在不考虑道路拓扑关系时产生的聚类结果
城市道路上存在大量交通标识的限制,例如红绿灯、转向、限行等。如果需要能更加精确地分辨出道路载客热点,必须考虑道路拓扑关系对载客点间距离计算的影响,即载客点间是否密度可达需要考虑二者之间的行程距离,如图3所示。

图3 道路网络中载客点间的距离
因此,在道路网络中,p与q之间的行程距离计算可写成:

一方面,城市道路中两点的距离一般是两点间的网络距离,可以通过计算两载客点之间的道路最短距离得到,可记为distsp(p,q);另一方面,在城市系统中由p至q如果经过路口,需要减速或停留,因此p与q之间的道路交叉口停驻时间distTime(p,q)同样应计算在可达性中,distTime(p,q)可通过计算道路交叉口数量N得到:

其中,WaitTimeavg为城市路口的平均停留时间,Speedavg为城市车辆的平均行程速度。在对点p查找邻近载客点时,可以用行程距离替代欧氏距离,从而实现这一目标。
1.3 顾及路网约束的载客点聚类算法流程
基于以上分析,本文设计了RL-DBSCAN算法,在计算两点间距离时,用行程距离dist(p,q)进一步判断,将欧氏距离邻近但是网络距离较远的载客点进行区分。具体算法如表1所示。
算法1 RL-DBSCAN主算法
输入: D — 全部载客点集合,eps — 邻域半径,mPts—最少载客点个数

10. ExpandCluster(p, NeighborPts, C, eps, mPts)
其中, ExpandCluster函数用于将邻近载客聚类簇进行合并。
算法2 生成聚类簇ExpandCluster
输入: p — 载客点,NeighborPts— 某点p的所有邻近载客点集合,C—新聚类载客数据集,eps — 邻域半径,mPts—最少载客点个数
1. add p to cluster C
2. for each point p' in NeighborPts
3. if p' is not visited
4. mark p' as visited
5. NeighborPts' = regionQuery(p', eps)
6. if Density (NeighborPts) < mPts
7. NeighborPts = NeighborPts joined with NeighborPts'
8. if p' is not yet member of any cluster
9. add P' to cluster C
2 系统实验与分析
本文的实验运行环境是Windows操作系统,实验的硬件配置是Intel(R) Core(TM)i5-4509 CPU@3.30 GHz八核CPU,内存为8 GB,算法采用python语言编写。
2.1 算法实验数据集
本文采用武汉市的出租车轨迹数据作为算法实验测试数据集,数据中包含有出租车编号、时间、出租车经纬度、方向(正N 0°,正E 180°)、速度(km)、ACC状态 (开:车是发动的,关:停车熄火) 、载客状态(0表示出租车空驶,1表示出租车载客)。
实验采用的数据集采用2014-05-01出租车轨迹数据,数据集覆盖地理空间的经度范围为[113°41',115°05'],维度范围为 [29°58',31°22'],区域面积约为1 171.70 km2,覆盖武汉市主城区及周边区域。包含了9 700辆车共1 130万条出租车定位数据。
2.2 数据预处理
原始数据以TXT文本形式保存,在进行载客点聚类之前,需要对原始数据进行预处理主要包括属性值异常数据剔除、数据空间化、坐标偏移数据剔除等。
GPS数据本身存在精度误差,在与武汉市基础地图数据叠加的时候会出现一定的偏离,导致载客点不在对应的出行路径上,影响GPS点提取道路信息的准确性,因此需要进行道路匹配。其基本原理是将待匹配的GPS点数据与路网数据进行对比,搜索出对应的道路线作为待匹配的样本。通过道路匹配算法,计算匹配样本与匹配点的匹配相似度,选取匹配相似度最高的匹配样本最为GPS点的最终匹配道路,获取浮动车轨迹点的准确定位点。
2.3 聚类结果统计
为了比较两种算法在不同参数条件下的聚类稳定性,本文分别选择了聚类簇中包含点的最小阈值分别为3、4、6、8,聚类半径eps在50 m、100 m、200 m、300 m、400 m、500 m时的类簇数量变化情况进行实验分析,结果如图4所示。可以发现,在加入道路约束后,聚类结果对聚类半径的阈值不敏感,当阈值增大到一定程度后聚类结果变化较小。聚类结果对聚类簇包含点的数量阈值较为敏感,不同的点数阈值得到的聚类结果差异较大。同时,在考虑道路约束的情况下,当聚类簇包含的最小点阈值不变时,聚类半径达到200 m后RL-DASCAN得到的聚类簇数量基本趋于稳定,不再随半径的变化而变化,而DBSCAN算法得到的类簇数量则根据聚类半径的变化而快速下降,这是因为当半径变大后,DBCSAN算法将更多邻近的类簇合并到了一起,而RL-DBSCAN算法中由于欧氏距离邻近的簇在行程距离下并不能形成合并,去除了部分聚类中的噪音。

图4 DBSCAN与RL-DBSCAN算法不同参数聚类数量统计
图5是比较在不同条件下两种算法生成的聚类簇所包含的平均载客点数。可以看出DBSCAN算法得到的聚类簇中平均载客点数量随着聚类半径的增加而不断增加,而RL-DBSCAN算法得到聚类簇包含的载客点数则始终变化较小。RL-DBSCAN算法得到的聚类簇大小受聚类半径和最小簇内点数量的参数影响较小,对于载客区域的精细提取与分析而言,这种结果可以更好地为分析某个微观区域的载客热度变化情况提供数据支持。
2.4 聚类效果实验分析
为了对比RL-DBSCAN和DBSCAN算法的差异,提取出一些典型区域(交叉路口,双向道路)的浮动车轨迹,对算法进行实验分析。实验结果表明,DBSCAN算法通常将处于道路交叉口处且密度比较大的轨迹点都归为一类(图6a),而RL-DBSCAN算法在处理交叉路口轨迹点时,对各个不同方向的轨迹点都能进行有效的聚类(图6b)。

图5 DBSCAN与RL-DBSCAN簇内平均载客点数量统计

图6 十字路口聚类结果
在处理对向道路上的轨迹点时,DBSCAN算法会笼统地将同一段路单方向不通的轨迹点聚类成簇(图 7a),这并不符合实际情况,RL-DBSCAN算法对于轨迹点之间距离的处理中加入了路网的限制,因此能有效处理双向道路的轨迹点聚类(图7b),不同方向的轨迹点即被归类成不同的簇,聚类结果更符合其空间数据的分布规律。
同时,选取武汉市几个具体的区域,将类别平均中心点作为热点,分别用DBSCAN和RL-DBSCAN算法提取同一时段的热点区域进行对比分析(图8)。提取的热点分别用绿色点和红色点表示,点的大小表示热点所在类别所包含的载客点数目的多少。

图7 双向道路聚类结果
从街道口附近热点图来看(图8a),RL-DBSCAN算法在武珞路上提取到鹏程蕙园小区路口及其马路对面、新世界百货、未来城小区门口以及未来城大酒店附近的热点,而DBSCAN算法提取出的热点偏离了道路,并不符合实际。汉口火车站附近(图8b),DBSCAN算法忽略了公交站牌处和车站南广场附近以及路边的多个热点,其显示的热点在地铁出口,而地铁附近并没有提取到上客点。改进算法不仅对载客热点区域进行了细致的提取,而且道路两边的热点信息也没有忽略。所以,对比DBSCAN算法,改进算法在提取热点时更加准确,更加符合实际情况。
2.5 聚类性能评价
由于载客点数据大多为历史数据,实地检验较为困难,本文从内部指标对两种聚类算法的结果进行比较。主 要 引 入 了 Dunn[12],Davies-Bouldin[13],Silhouette[14],I[15]等4种常见的聚类算法内部评价指标。它们都是通过计算各类中对象之间的距离以及类别之间对象的距离来衡量聚类质量的,即在类内紧密度和类间分离度之间寻找一个平衡点,其中Dunn、 Silhouette、I指标最大化时聚类效果最优,Davies-Bouldin是指标最小化时聚类效果最优。

图8 DBSCAN与RL-DBSCAN算法提取热点区域对比图
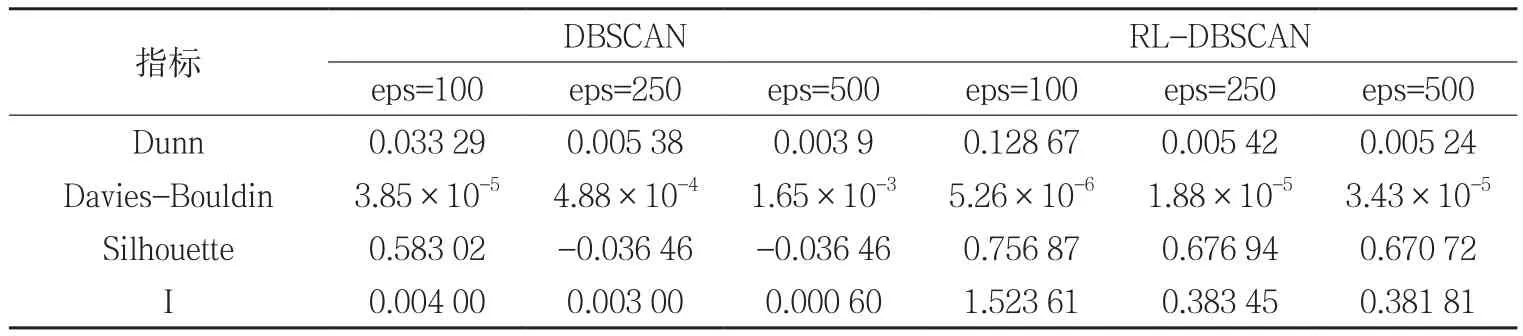
表1 两种算法的聚类评价指标比较
表1是两种算法在不同参数下各指标的计算情况,不论是DBSCAN还是RL-DBSCAN算法,各指标在eps=100时的值都优于其他情况,说明该参数下的聚类质量比其他参数下要好。对比在参数相同情况下两种算法的各个指标可发现,RL-DBSCAN算法的各个指标值普遍优于DBSCAN算法,进一步说明了RLDBSCAN算法在提取精细热点区域上的优势。
为了测试该算法的性能,抽取同一数据集分别采用DBSCAN算法、RL-DBSCAN算法进行试验并进行横向对比,结果如表1所示。从实验测试可知,虽然改进算法提取效果较好,由于算法在进行路网距离计算时花费时间较多,导致整个算法运行时间较长,所需内存也较大。所以算法在优化程度上有待进一步提高。

表2 算法性能测试
3 结 语
本文利用武汉市的出租车GPS轨迹数据,采用基于密度的DBSCAN算法对提取出的载客点进行聚类分析,提取载客热点区域。鉴于传统DBSCAN算法提取范围分布广的特点,根据出租车数据与道路数据的分布特征,将路网约束引入到传统的DBSCAN算法中,提出一种基于RL-DBSCAN算法的出租车载客数据聚类方法。该算法针对现有算法在出租车载客热点区域提取结果的不足,将道路拓扑关系及路段长度信息作为约束条件加入DBSCAN算法的点相似性判断中,并利用武汉市出租车GPS轨迹数据进行实验。实验结果表明,RL-DBSCAN算法对出租车载客热点区域的精确提取方面具有较好的效果,能更好地反映道路的载客热度。通过传统算法和改进算法的比较,证明改进算法对于道路两边或者十字路口处的载客点在提取效果上有一定的优势,但算法运行速度较慢,优化程度有待提高,在后期的研究中计划加入并行处理的方法,以提高计算速度。
[1] 柴彦威, 张文佳, 张艳,等. 微观个体行为时空数据的生产过程与质量管理:以北京居民活动日志调查为例[J].人文地理, 2009(6):1-9
[2] 吴志峰,柴彦威,党安荣,等. 地理学碰上“大数据”:热反应与冷思考[J].地理研究, 2015, 34(12): 2 207-2 221
[3] Qi G, Li X, Li S, et al. Measuring Social Functions of City Regions from Large-scale Taxi Behaviors[C].IEEE International Conference on Pervasive Computing & Communications, IEEE,2011:384-388
[4] Zheng Y, Liu Y, Yuan J, et al. Urban Computing with Taxicabs[C].International Conference on Ubiquitous Computing,ACM,2011:89-98
[5] Liu Y, Kang C,Gao S, et al. Understanding Intra-urban Trip Patterns from Taxi Trajectory Data[J]. Journal of Geographical Systems, 2012, 14(4):1-21
[6] Zheng Y, Capra L, Wolfson O, Yang H. Urban Computing:Concepts, Methodologies, and Applications[J]. ACM Transactions on Intelligent Systems & Technology, 2014, 5(3):222–235
[7] Tang J, Liu F, Wang Y, et al. Uncovering Urban Human Mobility from Large Scale Taxi GPS Data[J]. Physica A Statistical Mechanics & Its Applications,2015, 438(15):140-153
[8] Yuan J,Zheng Y, Xie X. Discovering Regions of Different Functions in a City Using Human Mobility and POIs[C].Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,ACM,2012. 186-194
[9] 廖律超, 蒋新华, 邹复民,等. 浮动车轨迹数据聚类的有向密度方法[J].地球信息科学学报, 2015(10):1 152-1 161
[10] Ester M, Kriegel H P, Sander J, et al. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise[C].KDD,1996, 96(34): 226-231
[11] 庄立坚,何兆成,杨文臣,等.基于大规模浮动车数据的交叉口转向规则自动提取算法[J].武汉理工大学学报(交通科学与工程版),2013, 37(5): 1 084-1 088
[12] Dunn J C. Well-Separated Clusters and Optimal Fuzzy Partitions[J]. Journal of Cybernetics, 2008, 4(1):95-104
[13] Hubert L J, Arabie P. Comparing Partitions[J]. J Classification,1985(2):193-218
[14] Rousseeuw P J. Silhouettes: A Graphical Aid to the Interpretation and Validation of Cluster Analysis[J]. Journal of Computational& Applied Mathematics, 1987, 20(20):53-65
[15] Maulik U, Bandyopadhyay S. Performance Evaluation of Some Clustering Algorithms and Validity Indices.[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2002, 24(12):1 650-1 654
P208
B
1672-4623(2017)10-0016-05
10.3969/j.issn.1672-4623.2017.10.005
2016-09-29。
项目来源:国家自然科学基金资助项目(41471326);中央高校基本科研业务费专项资金资助项目(204216kf0190)。(*为通讯作者)
江慧娟,硕士,研究方向为轨迹数据挖掘。

