浅析建筑排水用硬聚氯乙烯管材拉伸屈服强度测量不确定度

■ 许 静

(1.福建省交通科学技术研究所;2.福建省公路水运工程重点实验室，福州 350001)

浅析建筑排水用硬聚氯乙烯管材拉伸屈服强度测量不确定度

■ 许 静1，2

(1.福建省交通科学技术研究所;2.福建省公路水运工程重点实验室，福州 350001)

硬聚氯乙烯管材拉伸屈服强度是衡量建筑排水用硬聚氯乙烯管材质量的一个关键性指标。本文通过剖析拉伸屈服强度试验方法，并对试验结果的测量不确定度进行分析评定，最后，找出了影响拉伸屈服强度测量结果的主要因素，从而提高建筑排水用硬聚氯乙烯管材的质量。

硬聚氯乙烯管材 拉伸屈服强度 不确定度 评定

建筑排水用硬聚氯乙烯管材简称为UPVC或PVCU排水管，是以PVC树脂为主要原料，加入适量填充料及适宜的助剂，如稳定剂、改性剂、润滑剂等，经挤出机挤出成型而成。其拉伸屈服强度是评价PVC-U管材承受纵向外力特性的一项关键性指标。本文通过剖析拉伸屈服强度试验方法，并对试验结果的测量不确定度进行分析评定，最后，找出了影响拉伸屈服强度测量结果的主要因素。

1 试样制备及试验方法

按GB/T5836.1-2006《建筑排水用硬聚氯乙烯(PVCU)管材》标准(以下简称GB/T5836.1)规定，拉伸屈服强度按标准GB/T8804.2-2003《热塑性塑料管材 拉伸性能测定 第2部分：硬聚氯乙烯(PVC-U)、氯化聚氯乙烯(PVCC)和高抗冲聚氯乙烯 (PVC-HI)管材》(以下简称GB/T8804.2)和标准GB/T8804.1-2003《热塑性塑料管材拉伸性能测定 第1部分：试验方法总则》(以下简称GB/T8804.1)要求进行试验。

所用试验设备有：微机控制电子式万能试验机CMT4304(0.5级)和数显游标卡尺(精度0.01mm)。

本文选用白色、公称外径为110mm的建筑排水用硬聚氯乙烯(PVC-U)管材，按GB/T5836.1及GB/T8804.2进行试验，试样采用冲裁试样 (类型2)数量5个，按GB/T2918-1998《塑料试样状态调节和试验的标准环境》标准规定，在 (23±2)℃环境中进行状态调节，用精度为0.01mm的数显游标卡尺测量试样的宽度及最小厚度，计算试样原始截面积，调节试验机试验速度为 (5±0.5)mm/min；夹持试样尽量使其轴线与拉伸应力方向一致，对其施加轴向拉力，记录其达到屈服时的应力，通过计算得到拉伸屈服强度。试验结果以5个试样的算术平均值表示，结果保留三位有效数字，小数点后第1位有效数字按四舍五入处理。

2 数学模型

根据GB/T8804.2，拉伸屈服强度：

式中，σ——拉伸屈服强度，(MPa)；

F——屈服点的拉力，(N)；

A——试样的原始截面积，(mm2)；

b——试样平行部分宽度，(mm)；

h——试样最小厚度，(mm)；

m——试样个数。

根据JJF1059-1999《测量不确定度评定与表示》，测量不确定度主要来源有：

(1)重复性测量及样品不均性所引入的不确定度分量urel(rep)；

(2)屈服点拉力F测量误差所引入的不确定度分量urel(F)，包括试验机示值误差引入的不确定度urel1(F)、标准测力仪校准试验机引入的标准不确定度urel2(F)、计算机数据采集力值引入的标准不确定度urel3(F)；

(3)试样平行部分宽度b测量所引入的不确定度分量urel1(b)；

(4)试样最小厚度h测量所引入的不确定度分量urel1(h)；

(5)其他如试验速率的偏差、试验机的分辨力、试验环境条件引起的不确定度。因使用的微机控制试验机以一固定速率加载变化较小，分辨力较高，其引入的不确定度可忽略不计，同时测量时环境温度、湿度波动在标准要求范围波动较小，则其产生的不确定度亦忽略不计。

3 标准不确定度分量及其评定

3.1 重复性测量及样品不均性所引入的不确定度分量urel1(rep)

重复性引起的相对不确定度主要来源于拉力测量的重复性、试样平行部分宽度b测量的重复性和试样最小厚度测量的重复性。

试样采用白色、公称外径为110mm的建筑排水用硬聚氯乙烯(PVC-U)管材，壁厚为3.2mm，冲裁10个试样(类型2)进行试验，试验结果如表1所示。

表1 拉伸屈服强度试验结果

拉伸屈服强度σ平均值：

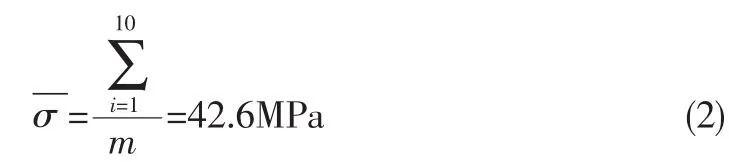
拉伸屈服强度σ标准偏差：

重复性引起的相对不确定度分量：

实际测量情况是在重复条件下连续测量5个，以5个试样的拉伸屈服强度试验结果的平均值为最终测量结果，得到拉伸屈服强度σ的标准不确定度：

3.2 屈服点拉力测量误差所引入的不确定度分量urel(F)

3.2.1 试验机最大允许示值误差引入的不确定度urel1(Fmax)

根据GB/T8804.1要求，材料试验机应能以恒定速率加载，示值相对误差不大于±0.5%，试验的最大荷载应在试验机示值的15%～90%之间。因此，本次试验采用微机控制电子式万能试验机CMT4304(配1kN的拉压力传感器，精度0.5级)，其最大允许示值误差为±0.5%，误差范围区间的半宽度为0.5%，示值误差出现在区间 [-0.5%，+0.5%]的概率是均匀的，并满足矩形分布，所以包含因子

3.2.2 标准测力仪校准试验机引入的标准不确定度urel2(F)

0.5级试验机是借助于0.2级标准测力仪进行校准的，则其最大允许误差为0.2%，包含因子为 。因此引入的B类评定相对标准不确定度为：。由此引入的B类评定相对标准不确定度为：

3.2.3 计算机数据采集力值引入的标准不确定度urel3(F)

由JJF1103-2003计量技术规范附录B.3可知，该不确定度与采样速率及系统的分辨率有关，一个合格的计算机数据采集系统所引入的B类相对标准不确定度为：

3.2.4 屈服点拉力F测量误差所引入的不确定度分量urel(F)

从上述三个方面的因素所引入的测量不确定度彼此独立不相关，所以屈服点拉力F测量误差所引入的不确定度分量urel(F)可合成为：

3.3 试样平行部分宽度b测量所引入的不确定度分量urel(b)

试样平行部分宽度b测量所引入的不确定度分量urel(b)由两部分组成：数显游标卡尺的示值误差导致的不确定度分量urel(b1)和操作者所引入的不确定度分量urel(b2)。按GB/T8804.1要求，建筑排水用硬聚氯乙烯(PVC-U)管材的拉伸屈服强度试验采用冲裁类型2试样，其试样平行部分宽度标准规定为6mm[0，+0.4mm]，其出现在此区间的概率是均匀的，为固定分量。

3.3.1 示值误差导致的不确定度分量urel(b1)

采用数显游标卡尺测量，精度为0.01mm，以均匀分布估计，。则示值误差所引入的不确定度为：

3.3.2 操作者所引入的不确定度分量urel(b2)

本次试验采用10件试样，各测3次，urel(b2)按合并样本标准差Sp(xk)贝塞尔公式计算：

其中，取m=1,n=3。

由测量数据计算得：

两者合成后，得到试样平行部分宽度b测量所引入的不确定度分量urel(b)：

3.4 试样最小厚度h测量所引入的不确定度分量urel(h)

试样最小厚度h测量所引入的不确定度分量urel(h)由两部分组成：数显游标卡尺的示值误差导致的不确定度分量urel(h1)和操作者所引入的不确定度分量urel(h2)。

按GB/T8804.1要求，建筑排水用硬聚氯乙烯(PVCU)管材的拉伸屈服强度试验采用冲裁类型2试样，试样的厚度为3.2mm，为固定分量。

3.4.1 示值误差导致的不确定度分量urel(h1)

采用数显游标卡尺测量，精度为0.01mm，以均匀分布估计，。则示值误差所引入的不确定度为：

3.4.2 操作者所引入的不确定度分量urel(h2)

本次试验采用10件试样，各测3次，urel(h2)按合并样本标准差Sp(xk)贝塞尔公式计算：

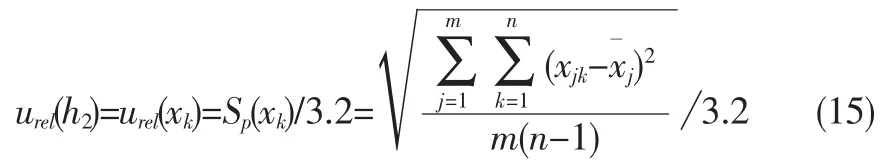
其中，取m=10,n=3。

由测量数据计算得：

两者合成后，得到试样平行部分宽度h测量所引入的不确定度分量urel(h)：

3.5 合成标准不确定度评定

由于各分量之间彼此独立，相对合成标准不确定度为：

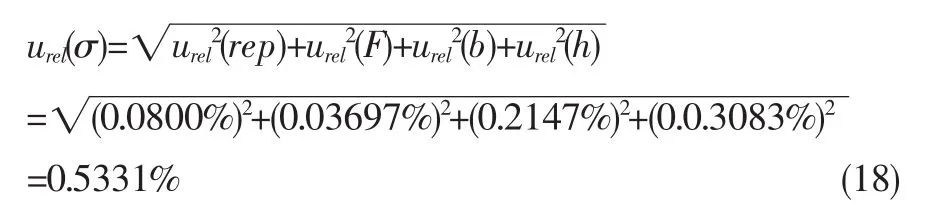
3.6 扩展不确定度评定

本例在报告合成标准不确定度时，缺少有关自由度的信息，这在使用计量仪器进行常规测量时是经常遇到的。实际上，估算B类标准不确定度时，都隐含地假设标准不确定度是确切知道的，这就暗示它们相应的自由度都趋近∞(亦即标准不确定度的相对不确定度趋近于零)。因此根据韦尔奇—萨特思韦特公式，合成标准不确定度Urel(TS)的有效自由度也趋近于∞。这就意味着，在相对合成标准不确定度Urel(TS)确定后，乘以一个包含因子k，即可得扩展不确定度Urel(TS)。根据JJF1059-1999《测量不确定度评定与表示》第7章可知，在大多数情况下包含因子k=2，区间的置信概率约为95%，故拉伸强度的相对扩展不确定度urel(TS)为：

绝对扩展不确定度为：

于是，本例试验检测测量结果可表示为：

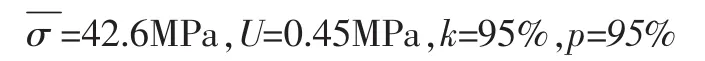
3.7 不确定度评定分析

相对标准不确定度分量汇总如表2。从表2可看出，重复性引起的不确定度分量对总的不确定度占的比例最大，需控制其影响因素。

对于选用的材料，拉伸屈服强度显然是高一些好，因此在设计标准或试验规范中通常希望σ大于某值 (下限)，而不会对其上限提出要求，本例标准规定σ≥40MPa，测量结果为σ=(42.6±0.45)MPa。k=2,p=95%如果标准要求σ＞43.05MPa，则结果评定不合格。但当标准要求为42.15MPa＜σ＜43.05MPa时，材料合格与否的判定就会处于可疑区、模糊区或不确定区。从这个讨论可看出，不确定度评定对产品质量的判定和试验数据的判断的重要性。

表2 相对标准不确定度一览表

4 结论

通过对硬聚氯乙烯管材拉伸屈服强度测量不确定度的评定，知道影响拉伸屈服强度检测结果的主要因素是试样制备和试验机最大允许示值误差，因此，试验实际操作时，应注意取样的均匀性，应考虑试样制备的方法、试样截面积的测量等对检测结果的影响，同时，试样的制备应尽量采用锋利的裁刀加工，以保证测量的准确性。

[1]GB/T 5836.1-2006，建筑排水用硬聚氯乙烯(PVC-U)管材[S]．

[2]GB/T 8804-2003，热塑性塑料管材 拉伸性能测定[S]．

[3]GB/T2918-1998，塑料试样状态调节和试验的标准环境[S]．

[4]JJF 1059.1-2012，测量不确定度评定与表示技术规范[S]．

[5]国家质量技术监督局计量司.测量不确定度评定与表示指南[M]．北京：中国计量出版社，2000：76-79.

[6]JJF 1103-2003，万能试验机计算机数据采集系统评定[S]．