Banach格上的b-Dunford-Pettis算子

李娇娇, 陈金喜, 陈滋利

(西南交通大学数学学院,四川 成都 611756)

Banach格上的b-Dunford-Pettis算子

李娇娇, 陈金喜, 陈滋利

(西南交通大学数学学院,四川 成都 611756)

为了进一步研究 Banach格上算子的性质,受b-序有界集和Dunford-Pettis集定义的启发,给出了b-Dunford-Pettis算子的定义,研究了该算子与b-AM-紧算子（Dunford-Pettis全连续算子,弱极限算子,序Dunford-Pettis算子）间的关系;利用b-Dunford-Pettis算子与Dunford-Pettis算子的共轭关系,证明了b-Dunford-Pettis算子满足控制性.

b-Dunford-Pettis算子;b-AM-紧算子;弱极限算子;相对紧Dunford-Pettis性质

1 引言和预备知识

近年来,关于 Banach格及其上的算子理论的研究中,主要讨论算子所在的空间性质和算子本身的性质.2003年，Alpay等[1]提出了 b-序有界集和空间具有 b-性质的概念,引入了Banach格上一类b-弱紧算子并讨论了其相关性质；2010年程娜[2]引入并讨论了一类 b-AM-紧算子；2016年，El Kaddouri等[3]根据 b-序有界集和极限集的定义引入 b-极限算子的概念并对其相关性质进行了研究.本文介绍一类定义在 Banach格上的新算子b-Dunford-Pettis算子,并研究该算子与b-AM-紧算子（Dunford-Pettis全连续算子,弱极限算子,序Dunford-Pettis算子）间的关系以及它的控制性.

本文中算子T:E→F代表全体有界线性算子.

在介绍主要结果之前,先介绍一些基本概念和已知结果.

定义 1.1[1]Banach格E中的一个子集A如果在E的拓扑二次共轭E′′中是序有界的,则称该集合为E中的b-序有界集.

定义 1.2[1]如果Banach格E中的b-序有界集均为序有界集,则称该空间具有b-性质.

序有界集一定是b-序有界的,反之不一定成立.例如:集合A={en:n∈N}在Banach格c0上是b-序有界的但不是序有界的[1].

定义1.3[2]设E和F为Banach格,如果算子T:E→F将E中b-序有界集映为F中的相对紧集,则称T为b-AM-紧算子.

引理 1.1[2]设E,F是Banach格,下列命题是等价的:

(1)算子S,T:E→F满足0≤S≤T.如果T是b-AM-紧的,则S是b-AM-紧的;

(2)下列条件至少有一个是成立的:

(a)E′是离散的;

(b)F有序连续范数.

定义 1.4[4]Banach格E中的范数有界子集A是Dunford-Pettis集,如果E′上的每一个弱零列(fn)在A上是一致收敛的,即

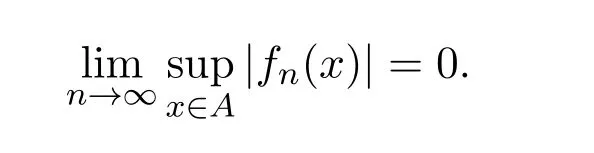
定义 1.5[5]如果Banach格E中的每一个Dunford-Pettis集是相对紧的,则称E有相对紧Dunford-Pettis性质.

例如,Schur空间和离散的KB空间有相对紧Dunford-Pettis性质[3].

定义 1.6[6]设E和F为Banach格,如果算子T:E→F将E中序有界集映为F中的Dunford-Pettis集，则称T为序Dunford-Pettis算子.

定义1.7[7]设E和F为Banach格,如果算子T:E→F将E中闭单位映为F中的Dunford-Pettis集,则称T为弱极限算子.等价地,T是弱极限算子如果对每一个弱零列

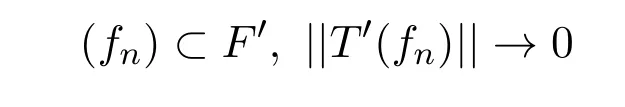
成立.

定义1.8[8]设E和F为Banach格,如果算子T:E→F将E中Dunford-Pettis集映为F中的相对紧集，则称T为Dunford-Pettis全连续算子.

其它未解释的有关Banach格和算子理论的一些概念、术语及符号详见文献[9,10].

2 b-Dunford-Pettis算子及与相关算子间的关系

定义2.1设E和F为Banach格,如果算子T:E→F将E中b-序有界集映为F中的Dunford-Pettis集,则称T为b-Dunford-Pettis算子.

下面给出关于b-Dunford-Pettis算子的一些主要结果.

定理2.1设E和F为Banach格,T:E→F是一个算子.则下列命题是等价的:

(1)T:E→F是b-Dunford-Pettis算子;

(2)对任意从F到Banach空间Z的Dunford-Pettis全连续算子S,S◦T是b-AM-紧算子;

(3)对任意Dunford-Pettis全连续算子S:F→c0,S◦T是b-AM-紧算子;

(4)对E中任意b-序有界列(xn)和F′中任意弱零列(fn),有fn(T(xn))→0成立.

证明(1)推出(2).令S:F→Z是一个Dunford-Pettis全连续算子,A是E中b-序有界集.因为T:E→F是b-Dunford-Pettis算子,则T(A)是F中的Dunford-Pettis集,从而S(T(A))是相对紧集.即证明了S◦T是b-AM-紧算子.

(2)推出(3).显然.

(3)推出(4).令A是E中b-序有界集,序列(xn)⊂A且(fn)是F′中任意弱零列.定义算子

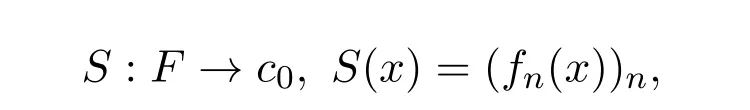
对任意x∈F.由文献[9]中定理5.26知,S是弱紧算子,再由文献[8]中推论1.1得到S是Dunford-Pettis全连续算子.

根据假设,S(T(A))是c0中的相对紧子集,由文献[9]3.2中练习14知,

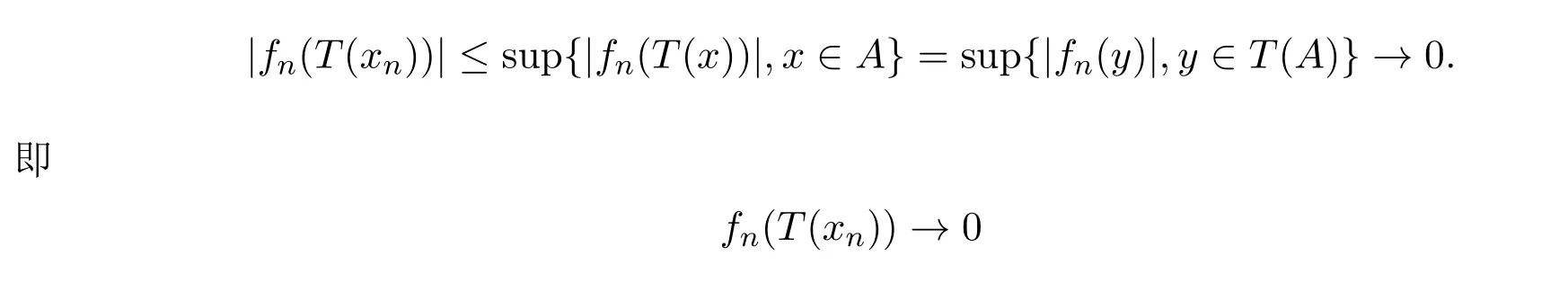
成立.

(4)推出 (1).令 A是 E中 b-序有界集.要证明 T(A)是 Dunford-Pettis集,根据Dunford-Pettis集的定义,只需证明F′中任意弱零列(fn),有

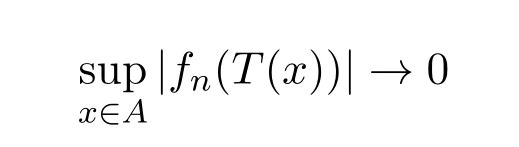
成立.假设不成立,则存在ε＞0和弱零列(fn)使得

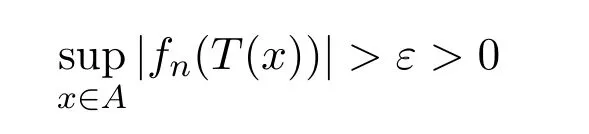
对所有n都成立.从而存在序列(xn)⊂A使得

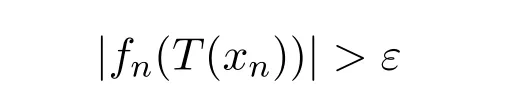
对所有n都成立,矛盾.因此,T(A)是Dunford-Pettis集,即T:E→F是b-Dunford-Pettis算子.

由定理2.1可以得到如下结论:

推论2.1设E是Banach格,下列命题是等价的:

(1)恒等算子IdE:E→E是b-Dunford-Pettis算子;

(2)对任意从E到Banach空间Z的Dunford-Pettis全连续算子S,S◦T是b-AM-紧算子;

(3)对任意Dunford-Pettis全连续算子S:E→c0,S◦T是b-AM-紧算子;

(4)对E中任意b-序有界列(xn)和F′中任意弱零列(fn),有fn(xn)→0成立.

如果一个算子T:E→F将E中b-序有界映为F中b-序有界,则称T是b-序有界算子.

记L(E,F)为从E到F的所有有界线性算子所构成的空间,Lb−DP(E,F)为所有从E到F的b-Dunford-Pettis算子构成的空间.那么可得到b-Dunford-Pettis算子构成空间的性质.

命题2.1设E,F,G是Banach格,则

(1)Lb−DP(E,F)是L(E,F)的一个范闭子空间;

(2)如果 T:E→ F是 b-Dunford-Pettis算子,则对任意算子 S:F→ G,S◦T是b-Dunford-Pettis算子;

(3)如果T:E→F是b-序有界算子,则对任意b-Dunford-Pettis算子S:F→G,S◦T是b-Dunford-Pettis算子.

证明(1)显然 Lb−DP(E,F)是 L(E,F)的向量子空间.只需证明 Lb−DP(E,F)是范数拓扑下的闭子空间.设S在Lb−DP(E,F)的范数闭包中,A为E中任一b-序有界集.对任意ε＞0,选择 T∈Lb−DP(E,F)使得

成立.因为 T是 b-Dunford-Pettis算子,所以 T(A)是 Dunford-Pettis集,由文献 [6]中引理 3.1知,S(A)也是 Dunford-Pettis集.即证明了 S是 b-Dunford-Pettis算子,由此说明Lb−DP(E,F)是L(E,F)的一个范闭子空间.

(2)设 T:E→F是b-Dunford-Pettis算子,A是 E中任一 b-序有界集,则 T(A)是Dunford-Pettis集,从而S(T(A))是Dunford-Pettis集.即 S◦T是 b-Dunford-Pettis算子.

(3)设 T:E→ F是 b-序有界算子,A是 E中任一 b-序有界集,则 T(A)是 b-序有界集.因为 S是 b-Dunford-Pettis算子,故 S(T(A))是 Dunford-Pettis集.即 S◦T是b-Dunford-Pettis算子.

下面结论给出空间或算子在满足什么条件时,该算子是b-Dunford-Pettis算子.

定理 2.2设T:E→F是从Banach格E到Banach格F的一个算子.如果下列任一条件成立,则T是b-Dunford-Pettis算子:

(1)E是离散的KB空间;

(2)T是b-序有界算子,F是离散的KB空间.

证明(1)设A是E中任一b-序有界集.因为E是离散的KB空间,由文献[11]中推论2.4知,A是范数相对紧的,则T(A)是相对紧的.从而T(A)是Dunford-Pettis集,即T是b-Dunford-Pettis算子.

(2)首先证明当F是离散的KB空间时,恒等算子IdF:F→F是b-Dunford-Pettis算子.设A是F中任一b-序有界集.因为F是KB空间,根据文献[1]中命题2.1,F有b-性质,从而A是序有界的.故A是几乎序有界的,即存在u∈F+使得A⊂[−u,u]+εBF.因为F离散且有序连续范数,由文献[12]定理 6.1得到[−u,u]是范数紧集.由文献[9]中定理 3.1知A是范数相对紧集,故A是Dunford-Pettis集,即IdF:F→F是b-Dunford-Pettis算子.由命题2.1,

是b-Dunford-Pettis算子.

注意到 b-Dunford-Pettis算子一定是序 Dunford-Pettis算子,弱极限算子一定是 b-Dunford-Pettis算子;反过来不一定成立.如果 Banach格 E是一个有序单位元的 AM 空间,那么E上的每一个范数有界集是序有界的,此时,每一个序Dunford-Pettis算子一定是弱极限的.

下面命题给出了b-Dunford-Pettis算子,序Dunford-Pettis算子,弱极限算子三者等价的充分条件.

命题 2.2设E是一个有序单位的AM 空间,F是Banach格,则下列命题等价:

(1)T:E→F是弱极限算子;

(2)T:E→F是b-Dunford-Pettis算子;

(3)T:E→F是序Dunford-Pettis算子.

下面定理给出了当任意b-Dunford-Pettis算子是弱极限算子时的必要条件.

定理 2.3设E和F是Banach格.如果每一个正的b-Dunford-Pettis算子T:E→F是弱极限的,则下列条件至少有一个是成立的:

(1)F′有正的 Shur性质;

(2)E′的范数是序连续的.

证明(用反证法)假设F′没有正的Shur性质且E′的范数不是序连续的.需要构造一个正的b-Dunford-Pettis算子但不是弱极限的.事实上,如果E′的范数不是序连续的,由文献[10]中定理2.4.14和命题2.3.11可知,E中存在与ℓ1同构的闭子格,且存在正投影P:E→ℓ1;另一方面,因为F′没有正的Shur性质,则存在正的弱零列(fn)⊂F′使得||fn||=1对所有n成立.进而存在序列满足||yn||≤1且存在ε＞0使得

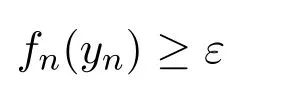
对所有n成立.

现在,考虑正算子

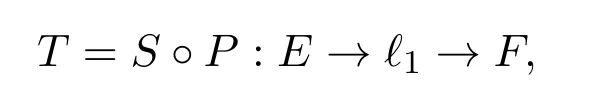
其中算子S定义为:

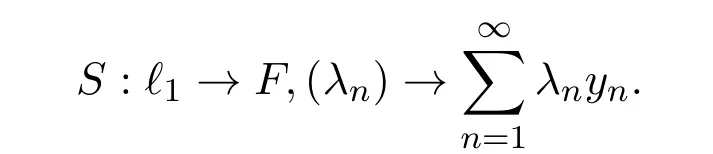
因为ℓ1是离散的KB空间,由定理2.2知,S是b-Dunford-Pettis算子.另一方面,P是正算子,从而是b-序有界算子.根据命题2.1可得到T是b-Dunford-Pettis算子.

但不是弱极限的.事实上,因为映射P:E→ℓ1是满的,则存在δ＞0使得δ·Bℓ1⊂P(BE).因此,

对所有n成立.但由于(fn)是F′中的弱零列,有

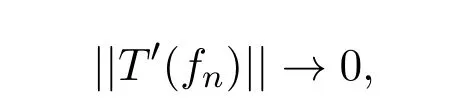
矛盾.即T不是弱极限算子.

很显然每一个b-AM-紧算子是b-Dunford-Pettis算子,但反之不一定成立.事实上,算子T:c0→ℓ∞是极限算子[9](从而是弱极限算子),故为b-Dunford-Pettis算子.但不是b-AM-紧的(因为c0不是KB空间)[11].然而,下面结论给出了b-Dunford-Pettis算子是b-AM-紧算子时空间所满足的条件.

命题2.3设E,F是两个Banach格,F有相对紧Dunford-Pettis性质.则下列条件是等价的:

(1)T:E→F是b-AM-紧算子;

(2)T:E→F是b-Dunford-Pettis算子.

证明(1)推出(2).显然.

(2)推出(1).如果T:E→F是b-Dunford-Pettis算子.因为F有相对紧Dunford-Pettis性质,则恒等算子IdF:F→F是Dunford-Pettis全连续算子.由定理2.1可知,

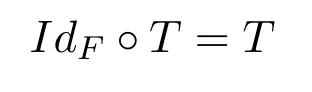
是b-AM-紧算子.

3 b-Dunford-Pettis算子的控制性

b-Dunford-Pettis算子是否满足控制性?即如果S,T:E→F是两个正算子满足0≤S≤T且T是b-Dunford-Pettis算子,那么S是不是b-Dunford-Pettis算子?答案是肯定的.

由文献 [9]中定理 4.21 知,对任意 0 ≤ x′′∈ E′′,在范数 ||·||∞下由 x′′生成的主理想 Ix′′定义为:

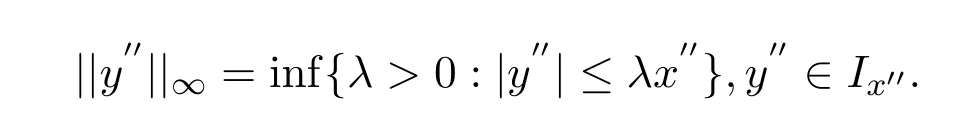
则 Ix′′是一个有序单位的 AM 空间,且其闭单位球是序区间 [−x′′,x′′].

命题 3.1设E和F是Banach格,T:E→F是一个算子.则下列条件是等价的:

(1)T是b-Dunford-Pettis算子;

(2)对任意 0≤x′′∈E′′,T|Y:Y →F 是弱极限算子,其中

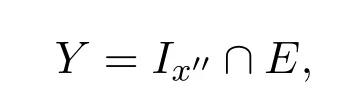
T|Y是将T限制在Y上.

证明(1)推出 (2). 任取 0≤x′′∈E′′,令 Y=Ix′′∩E.因为 Y 的闭单位球

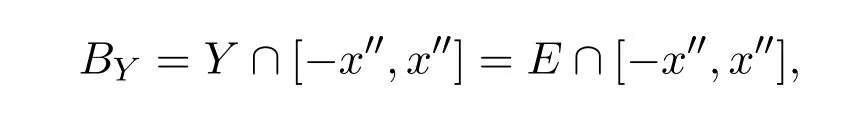
BY是E中b-序有界集.T是b-Dunford-Pettis算子,

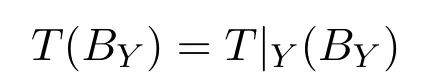
是Dunford-Pettis集,即T|Y:Y→F是弱极限算子.

(2)推出(1).设A是E中任一b-序有界集,要证明T(A)是F中的Dunford-Pettis集.选取 0 ≤ x′′∈ E′′使得 A ⊂ [−x′′,x′′]且 Y 和 Ix′′同上述定义,T|Y:Y → F 是弱极限算子.因为 A⊂BY,则有T|Y(A)是Dunford-Pettis集，即T(A)是 Dunford-Pettis集.如此就证明了T是b-Dunford-Pettis算子.

注 3.1设T:E→F是一个算子,(fn)是F′中的弱零列,由等式

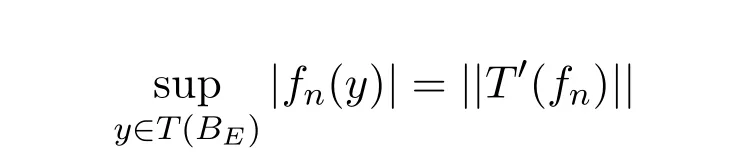
知,T是弱极限算子当且仅当T′是Dunford-Pettis算子.

结合命题3.1和注3.1可以得出下面的引理；

引理 3.1设E,F是Banach格,T:E→F是一个算子.T是b-Dunford-Pettis算子当且仅当对任意 0 ≤ x′′∈ E′′,算子

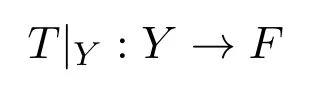
的共轭算子是Dunford-Pettis算子.

下面结果证明了b-Dunford-Pettis算子满足控制性质.

定理 3.1设E,F是Banach格,S,T:E→F是两个算子满足0≤S≤T.如果T是b-Dunford-Pettis算子,则S也是b-Dunford-Pettis算子.

证明设S,T:E→F是两个算子满足0≤S≤T且T是b-Dunford-Pettis算子.对任意 0 ≤ x′′∈ E′′,

因为T是b-Dunford-Pettis算子,由引理3.1知,

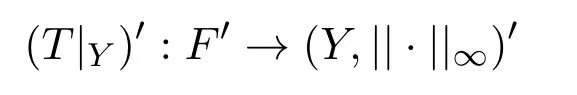
是Dunford-Pettis算子.又因Y′有序连续范数,根据文献[13]定理4.4,

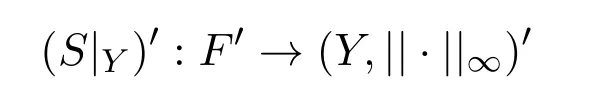
是Dunford-Pettis算子.再由引理3.1可知,S是b-Dunford-Pettis算子.

下面给出当每一个b-Dunford-Pettis算子是b-AM-紧算子时的必要条件.

定理3.2设E,F是Banach格.如果每一个正的b-Dunford-Pettis算子是b-AM-紧的,则下列条件至少有一个成立:

(a)E′是离散的;

(b)F有序连续范数.

证明设算子S,T:E→F满足0≤S≤T且T是b-AM-紧的,那么T是b-Dunford-Pettis算子.由定理 3.1知,S是b-Dunford-Pettis算子,由假设知S是 b-AM-紧算子,最后,由引理1.1得出结论.

[1]Alpay S,Altin B,Tonyali C.On property(b)of vector lattices[J].Positivity,2003,7(1):135-139.

[2]Cheng N,Chen Z L.b-AM-compact operators on Banach lattices[J].Chinese J.Eng.Math.,2010,27(4):753-756.

[3]El Kaddouri A,El Fahri K,Moussa M.The class of b-limited operators[J].Acta Sci.Math.(Szeged),2016,82:165-173.

[4]Aqzzouz B,Bouras K.Dunford-Pettis sets in Banach lattices[J].Acta Math.Univ.Comenianae,2012,81(2):185-196.

[5]Emmanuele G.Banach spaces in which Dunford–Pettis sets are relatively compact[J].Arch.Math.,1992,58(5):477-485.

[6]Bouras K,El Kaddouri A,H′michane J,et al.On the class of order Dunford-Pettis operators[J].Mathematica Bohemica,2013,138(3):289-297.

[7]林鸿钊.Banach空间中极限集与极限算子的弱化[J].纯粹数学与应用数学,2011,27(5):650-655.

[8]Wen Y M,Chen J X.Characterizations of banach spaces with relatively compact Dunford-Pettis sets[J].Adv.in Math.(China),2016,45:122-132.

[9]Aliprantis C D,Burkinshaw O.Positive Operators[M].Dordrecht:Springer-Verlag,2006.

[10]Meyer-Nieberg P.Banach Lattices[M].Berlin:Springer-Verlag,1991.

[11]Aqzzouz B,H’Michane J.The class of b-AM-compact operators[J].Quaestiones Mathematica,2013,36(3):309-319.

[12]Wnuk W.Banach Lattices with Order Continuous Norms[M].Warszawa:Polish Scienti fi c Publishers PWN,1999.

[13]Kalton N J,Saab P.Ideal properties of regular operators between Banach lattices[J].Illinois J.Math.,1985,29(3):382-400.

B-Dunford-Pettis operators on Banach lattices

Li Jiaojiao,Chen Jinxi,Chen Zili
(College of Mathematics,Southwest Jiaotong University,Chengdu 611756,China)

For the further study of the property of operators on Banach lattices,we give the de fi niton of b-Dunford-Pettis operator in light of the de fi nition of b-order bounded set and Dunford-Pettis set,and study the relationship between b-Dunford-Pettis operator and b-AM-compact operator(Dunford-Pettis completely continuous operator,weakly limited operator,order Dunford-Pettis operator)in this paper;By means of the conjugate relation between b-Dunford-Pettis operator and Dunford-Pettis operator,it was proved that b-Dunford-Pettis operator has the dominated property.

b-Dunford-Pettis operator,b-AM-compact operator,weakly limited operator,relatively compact Dunford-Pettis property

O177

A

1008-5513(2017)05-0513-09

10.3969/j.issn.1008-5513.2017.05.009

2017-08-30.

国家自然科学基金(11301285).

李娇娇(1993-),硕士生,研究方向：泛函分析.

2010 MSC:46B42