电容式降雨传感器及其特性曲线拟合方法*
张 龙, 杨长业, 王晓蕾, 叶 松
(解放军理工大学 气象海洋学院,江苏 南京 211101)
电容式降雨传感器及其特性曲线拟合方法*
张 龙, 杨长业, 王晓蕾, 叶 松
(解放军理工大学气象海洋学院,江苏南京211101)
针对将电容式传感器应用于降雨测量时,特性曲线的非线性误差较大问题,分别采用最小二乘曲线拟合法和径向基函数(RBF)神经网络对其输出特性曲线进行拟合。结果表明:RBF神经网络模型具有更强的非线性映射能力,其拟合精度明显高于最小二乘多项式模型。
电容式降雨传感器; 曲线拟合; 最小二乘法; 径向基函数神经网络; 均方误差
0 引 言
准确测量降雨已成为气象、水文、环境等多个领域的研究重点。降雨测量仪器多种多样,20世纪70年代以来,国外相继出现了基于光学法、振动法、摄像法等多种原理的降雨测量仪器[1,2]。受技术水平限制,国内降雨测量仪器发展较慢,气象观测业务中采用的雨量筒、翻斗式雨量计等观测设备仍存在较大测量误差。将电容式传感器应用于降雨测量,选用同轴圆柱型电容传感器作为感应原件,通过二极管双T型电路将降雨量转换为电压信号。因受边缘效应和寄生电容的影响,传感器输出特性曲线存在较大的非线性误差,采用传统的线性拟合方法无法准确描述传感器的输入输出关系。为减小传感器的非线性误差,文献[3~5]分别运用最小二乘多项式曲线拟合法、三次样条函数模型以及非线性反函数法对传感器的非线性特性进行补偿,均取得了一定的补偿效果。但是,三次样条函数模型和非线性反函数模型的补偿误差较大;最小二乘多项式曲线拟合法应用受到拟合数据量的限制,当数据量较大时容易出现振荡现象,无法获得多项式系数。径向基函数(radial basis function,RBF)神经网络结构简单且学习收敛速度快,能够以任意精度逼近非线性函数,适用于传感器特性曲线的拟合[6]。
本文分别选用最小二乘多项式模型和RBF神经网络模型对传感器输出特性曲线进行拟合,并对拟合结果进行比较。结果表明:RBF神经网络模型具有更强的非线性映射能力,其拟合精度明显优于最小二乘多项式模型。
1 传感器工作原理
1.1 传感器结构
采用同轴圆柱型结构,如图1所示。根据变介电常数型电容传感器的工作原理,在忽略边缘效应的前提下,传感器电容值C的计算公式为
C=+
(1)
式中r1和r2分别为内电极外半径和外电极内半径;ε和ε0分别为雨水和空气的介电常数;h和hx分别为电极高度和降雨高度。

图1 传感器结构
1.2 信号调理电路
信号调理电路主要包括电桥电路、二极管双T型网络、差动脉冲调宽电路以及CAV444电容电压线性转换集成电路等[7]。相比于其他电路,二极管双T型网络具有以下优点:线路简单,有效缩短了电容引线,减小了分布电容的影响;输出阻抗与电容大小无关,克服了电容式传感器高内阻的缺点;输出电压与传感器电容值满足线性关系,适用于具有线性特性的电容式传感器。基于此,本文选取了二极管双T型网络作为传感器的信号调理电路。
电路原理如图2所示。电源为幅值为±UE、占空比为50 %、周期为T的方波。
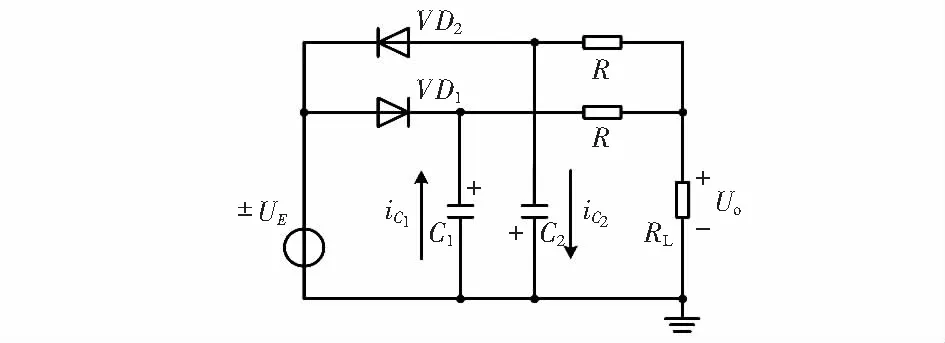
图2 信号调理电路
当电源幅值为正时,二极管VD2开路,VD1短路,电容C1以极短的时间充电,其影响可忽略,电容C2的初始电压值为UE。根据一阶电路时域分析的三要素法,得出通过电容C2的电流平均值IC2为
IC2=UEC2
(2)
同理,当电源电压幅值为负时,通过电容C1的平均电流IC1为
IC1=UEC1
(3)
则在负载RL上产生的电压为
Uo=(C1-C2)
(4)
设C1为传感器电容,C2为与C1初值相同的固定电容,令=K,将式(1)代入式(4),可得输出电压Uo与降雨高度hx的关系为
(5)
由上述理论分析可知,当传感器与信号调理电路参数确定时,输出电压Uo与降雨高度hx满足线性关系。然而在传感器的实际研制过程中,因极间寄生电容和边缘效应的影响,传感器的输出特性难以满足线性关系。
2 RBF神经网络
RBF是一种结构简单、收敛速度快、能够任意逼近非线性函数的网络[8]。
2.1 RBF网络模型[9]
实际应用中,为使网络的实现更加方便,习惯选用广义RBF网络,其结构如图3所示。

图3 广义RBF神经网络结构
2.2 RBF网络学习算法
假设训练样本有N个,广义RBF网络的输入层有M个神经元,隐含层有I(I 在RBF网络中最为常用RBF为高斯函数[10,11],其函数表达式为 (6) 式中 ‖Xk-Ci‖为欧几里得范数;Xk为第k个输入样本;Ci为高斯函数中心;σi为高斯函数标准差。 设对网络进行训练的样本集为X=[X1,X2…Xk…XN]T,输入任一训练样本Xk=[Xk1,Xk2…Xkm…XkM],k=1,2,…,N,网络第j个输出层神经元的实际输出为 (7) 当基函数为高斯函数时,其标准差为 σi= (8) 式中dmax为所选取的中心之间的最大距离;I为隐含层节点个数。 隐含层至输出层的权值可由最小二乘法直接求得,其计算公式为 (9) 对传感器进行静态标定,获得传感器3个循环过程的正、反行程标定数据。计算各个标定点处传感器输出电压的平均值,作为传感器的标定数据。采用最小二乘法对传感器标定数据进行一阶线性拟合,拟合结果如图4所示。 图4 一阶线性拟合结果 在采用直线拟合线性化时,传感器的实际特性曲线与拟合直线之间的最大偏差称为非线性误差,通常用相对误差γL表示,其计算方法为[8] γL=±(ΔLmax/yFS)×100 % (10) 式中 ΔLmax为最大非线性误差;yFS为满量程输出值。 经计算得传感器的非线性误差γL为14.95 %。由此可知:边缘效应和寄生电容等影响因素严重降低了传感器特性曲线的线性度,使得传感器的实际输出特性与理论推导结果产生较大的差异。为进一步提高拟合精度,采用三阶多项式对传感器标定数据进行拟合,结果如图5所示。比较图4和图5可知,多项式阶数越高,逼近能力越强,拟合误差越小。 图5 三阶多项式拟合结果 将传感器各标定点作为网络的输入量,对应的电压值作为网络的理想输出量。在Matlab环境下完成RBF网络的模型建立和参数设置。输入训练样本,对网络进行训练,利用RBF网络模型对传感器的输出特性曲线进行拟合。经过51次权值和阈值调整,拟合误差达到了预设范围,其误差收敛曲线如图6所示,拟合结果如图7所示。 图6 RBF神经网络误差收敛曲线 图7 RBF网络拟合结果 定义误差比较准则为均方误差[8](MSE) (11) 式中N为标定点个数;ei为各标定点处的拟合误差。 求解上述3种模型的均方误差和最大拟合误差,可得表1所示结果。结果表明,RBF网络模型的拟合效果明显优于最小二乘多项式拟合模型。 表1 3种模型拟合误差比较 传感器标定过程共进行3个循环,产生了6组标定数据,将6组数据作为检验样本对3种模型的拟合效果进行验证,得到如图8所示的拟合误差曲线。求解6组检验样本在3种模型下的最大拟合误差和均方误差,结果如表2所示。 图8 6组检验样本拟合误差曲线 误差样本1样本2样本3样本4样本5样本6误差最大值RBF网络模型三阶多项式模型一阶线性模型0.00680.11270.42200.00300.11310.42250.00650.10900.41800.00720.10390.41630.00750.10690.41480.00150.10930.4179均方误差RBF网络模型/10-5三阶多项式模型一阶线性模型1.18830.00240.02451.07780.00240.02451.27000.00240.02431.16410.00230.02461.12750.00240.02422.30330.00240.0243 由表2可知:RBF网络模型的拟合效果明显优于基于最小二乘法的一阶线性拟合模型和三阶多项式拟合模型。 本文将电容式传感器应用于降雨测量,并对其可行性进行了理论分析和实验验证。因受到寄生电容和边缘效应等因素的影响,传感器的输出特性曲线非线性误差较大,采用一阶线性拟合难以准确表达传感器的输入输出特性。为提高拟合精度,分别采用了最小二乘多项式模型和RBF网络模型对传感器的输出特性曲线进行拟合。实验结果表明:RBF网络模型具有更强的非线性映射能力,其拟合精度明显高于最小二乘多项式模型。对于电容式传感器而言,温度及介质的离子浓度均对传感器的测量特性产生较大影响。针对该问题,将设计更为合理的实验对其做进一步研究。 [1] 刘清惓,朱俊丰,杜 虹,等.基于压电效应的FPGA降水粒子测量系统设计[J].传感器与微系统,2014,33(3):85-88. [2] 岑家生,王青梅,罗 晖,等.降水粒子的成像探测技术及仪器初探[J].大气与环境光学学报,2011,6(6):415-422. [3] 姜德生,高 翩,张 翠,等.基于最小二乘法的光纤光栅Bragg波长直线拟合[J].传感器与微系统,2006,25(6):25-27. [4] 江 东,单 薏,刘绪坤,等.函数拟合法力数字传感器的非线性和温度补偿[J].传感器与微系统,2016,35(2):16-18. [5] 黄开志,黄 耀.一种基于反函数的传感器标定方法[J].传感器世界,2009,15(5):32-34. [6] 杨进宝,倪芳英,张建军.基于RBFNN的称重传感器温度误差补偿[J].传感器与微系统,2011,30(6):39-41. [7] 唐文彦.传感器[M].北京:机械工业出版社,2006. [8] Kurban T,Besdok E.A comparison of RBF neural network trai-ning algorithms for inertial sensor based terrain classification[J].Sensors,2009,9(8):6312-6329. [9] 侯立群,张智娟,仝卫国.基于RBF神经网络的传感器非线性误差校正方法[J].传感器技术,2004,23(3):43-45. [10] Lee C M,Ko C N.Time series prediction using RBF neural networks with a nonlinear time-varying evolution PSO algorithm[J].Neurocomputing,2009,73(1-3):449-460. [11] 王 晓,杨祖安,彭碧辉.改进型RBF神经网络在磁致伸缩液位传感器中的应用[J].自动化技术与应用,2015,34(12):5-8. Capacitiverainsensorandfittingmethodsof ZHANG Long, YANG Chang-ye, WANG Xiao-lei, YE Song (CollegeofMeteorologyandOceanography,PLAUniversityofScienceandTechnology,Nanjing211101,China) Aiming at problem of large nonlinear error of characteristic curve of capacitive sensor applied to measurement of rainfall,least square curve fitting method and radial basis function(RBF)neural network are used to fit output characteristic curve.The results show that the RBF neural network model has stronger nonlinear mapping ability,and its fitting precision is significantly higher than that of the least square polynomial model. capacitive rain sensor; curve fitting; least square method; radial basis function(RBF) neural network; mean square error 10.13873/J.1000—9787(2017)10—0027—04 2016—10—20 国家自然科学基金资助项目(40976062);江苏省自然科学基金资助项目(BK2009062);国家自然科学基金青年科学基金资助项目(41406107) P 414.9 A 1000—9787(2017)10—0027—04 张 龙(1992-),男,硕士研究生,主要研究方向为测控技术与仪器,E—mail:zhanglonglxy@163.com。杨长业(1964-),男,通讯作者,硕士,副教授,从事测试计量技术及仪器研究工作,E—mail:2558185157@qq.com。3 模型建立与结果分析
3.1 最小二乘多项式拟合模型


3.2 RBF网络拟合模型


3.3 拟合结果比较

3.4 拟合模型验证
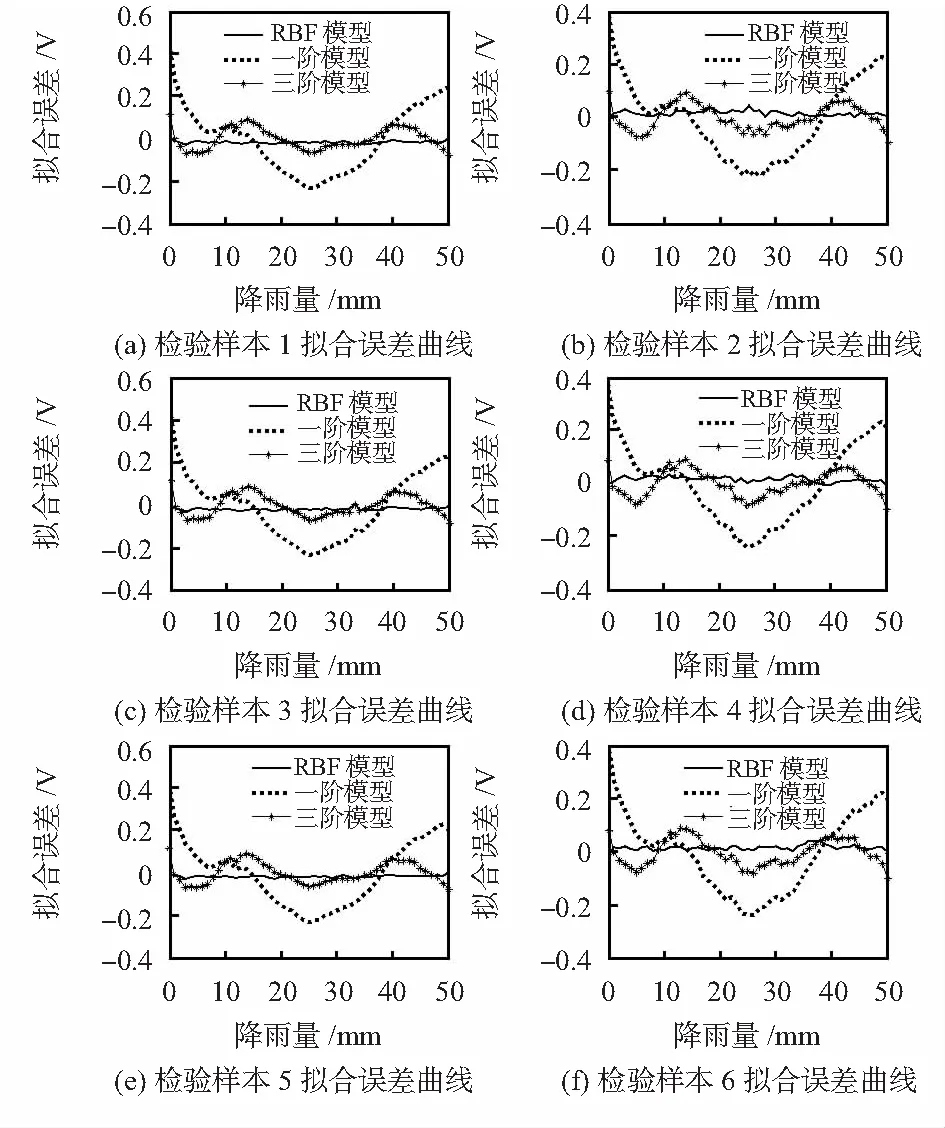

4 结束语
itscharacteristiccurve*

