社会情感算法优化神经网络的短时交通流预测
张 军, 胡震波, 朱新山, 王远强
(天津大学 电气与自动化工程学院,天津 300072)
社会情感算法优化神经网络的短时交通流预测
张 军, 胡震波, 朱新山, 王远强
(天津大学电气与自动化工程学院,天津300072)
针对反向传播(BP)神经网络用于交通流预测易陷入局部最优且寻优速度慢的问题,采用了社会情感优化(SEO)BP神经网络的参数,以SEO中的个体为一个BP神经网络,以3种情绪为表现形式,通过个体间的合作竞争进行寻优。运用Levy、正态、柯西分布3种情绪随机选择策略,通过不同方式实现了以不同的概率选择不确定的情绪,使SEO中情绪更好地模拟人的正常心理变化。实验表明:该模型较其他模型更有利于搜寻全局最优解,能有效提高短时交通流的预测精度。
城市交通; 短时交通流预测; 社会情感优化算法; 交通流; BP神经网络
0 引 言
交通流预测模型应具备实时性、准确性、可靠性。短时交通流量预测模型,大体可分为以下两类[1~3]:1)时间序列分析的方法,包括参数回归模型、ARIMA模型、Kalman滤波模型等;2)以模拟技术、神经网络、模糊控制等现代科学技术手段为基础的预测方法,其中有非参数回归模型、小波神经网络、多种与智能算法相结合的复合预测模型等。神经网络在摆脱建立精确的数学模型、拟合任意复杂的非线性问题上具有独特的优势,其中的反向传播(back propagation,BP)神经网络运用最为广泛,不过其明显不足是易陷入局部最优和寻优速度慢。
本文采用社会情感优化(social emotional optimization,SEO)算法来训练优化BP神经网络预测模型,并进一步将情绪的3种随机选择策略引入到SEO算法中,最后利用得到的模型对北京二环上的目标路段进行交通流短时预测分析。
1 BP神经网络与SEO算法
1.1 BP神经网络
典型的BP神经网络具有三层结构,分别为输入层、隐含层和输出层,其训练学习包括前向和反向过程。训练过程中,前向过程在某个训练样本作用于输入端后,利用当前权值计算神经网络的输出,实现信号从输入到隐含层再到输出层的过程。计算所得到的输出与已知输出之间的误差,并根据此误差对输出层权值的偏导数修正输出层的权值,再将误差反向传递到倒数第二层的各节点上,根据误差对这些节点权值的偏导数修正这些权值,依次下去,直至每层的权值均修正一遍。然后,从训练集中抽取出另一个样本进行同样的训练过程。如此不断地进行下去,直至达到预定精度,或者达到预设的训练次数,训练过程终止。
算法缺点为易陷入局部极值点。
1.2 SEO算法
在SEO算法[4~8]中,每次迭代,个体将根据相应的情绪指数选择行为,并依据社会对此行为评价的优劣调节其情绪指数。
首先初始化个体的社会状态,并将所有个体的情绪指数均设为1(最大值),按以下方式第一次更新个体的社会状态,即

(1)
式中xi(0)为处于初始化的个体i;ci为学习因子,i=1,2,3;ri为服从均匀分布的随机数,i=1,2,3;xn(0)为初代中社会评价最低的N个个体,用来为个体i的决策提供参考。
第t代时,如果个体i的社会评价劣于t-1代,则该个体由于不成功的决策会使其情绪指数下降
Ei(t+1)=Ei(t)-Δ
(2)
式中 参数Δ可设为0.05。若Ei(t+1)<0,则令Ei(t+1)=0。
如果个体i获得目前为止最高的社会评价,则其情绪指数会大幅度提高,于是将其情绪指数设置为
Ei(t+1)=1
(3)
依据不同的情绪指数,个体会选择不同的决策更新其社会状态:
1)当Ei(t+1) xi(t+1)=xi(t)+c1r1(xibest(t)-xi(t))- (4) (5) 式中xibest(t)为个体i直至第t代的最优社会状态,f(x)为个体的社会评价函数。 2)当m1≤Ei(t+1) xi(t+1)=xi(t)+c1r1(xibest(t)-xi(t))+ c2r2(Appraisebest(t)-xi(t))- (6) 式中Appraisebest(t)为群体直至第t代的最优社会状态,设群体规模为C,则 (7) 3)当Ei(t+1)≥m2时,认为个体情绪高昂,表现为学习渴望强烈,会因此忽略他人失败的经验,仅关注他人成功的经验,故决策方式如下 xi(t+1)=xi(t)+c2r2(Appraisebest(t)-xi(t)) (8) 1)确定SEOBP神经网络结构及相关参数。 根据对问题的分析确定BP神经网络的输入层神经元数目I、隐含层神经元数目H、输出层神经元数目O,设置社会种群规模C、情绪阈值m1和m2、学习因子ci,i=1,2,3,个体社会状态范围及最大迭代次数。 2)建立SEO中个体与BP需要优化的参数的映射关系。 一个3层BP神经网络需要优化参数可以用一个一维向量来表示 (9) 第1部分为输入层到隐含层的连接权值;第2部分为隐含层阈值;第3部分为隐含层到输出层的连接权值;第4部分为输出层阈值,这些待优化参数构成了SEO中的个体,个体的维度D为 D=I×H+H+H×O+O (10) 3)种群初始化,每个个体的初始社会状态均匀分布在设定的范围上。 4)确定个体的社会评价函数,计算个体的情绪指数。 每个个体对应一个BP神经网络,训练样本的输出值与实际值之间的误差作为个体的社会评价值,可采用均方误差(MSE)或均方根误差(RMSE)表示 (11) (12) 5)根据式(4)、式(6)、式(8)更新个体的社会状态。 6)根据式(5)、式(7)分别更新个体、群体最优状态。 7)算法终止输出最优网络。 如果满足最大迭代次数,或训练误差小于设定值,则算法终止,输出群体最优解。 标准SEO算法在模拟选择情绪时采用线性更新模式,即通过设置情绪阈值实现,考虑到情绪变化的不确定性[9,10],本文引入以下3种情绪的随机选择策略,并在实验中用实测的北京二环交通流数据验证哪种策略更有利于寻求全局最优解。 Levy分布具有两个参数:α,γ,0<α≤2,γ>0,且α用于控制分布的形状。Levy分布的概率密度函数为 (13) 算法中,所有个体的三种情绪的强度值在初始化阶段均服从相同的Levy分布L(0.8,2.5),此后调整γ来引导个体情绪对其社会评价进行反馈:在第t代,假设个体的三种情绪(低落、平和及高昂)具有不同分布L(0.8,γ1),L(0.8,γ2)和L(0.8,γ3),由此,随机产生3个随机数。显然,最大的随机数所对应的情绪最强烈,将其选出,作为个体i所表现出的情绪。在个体i决策后,如果其社会评价优于t-1代,则表明该情绪对个体的行为起到了积极影响,所以,要增加γ来提高该情绪被再次选中的可能,即γ′=γ+0.6;否则,减小其被选中的概率,即γ′=γ-0.9。即通过改变γ来调节情绪的强度,从而实现个体对情绪的不同选择。 在初始化阶段将所有个体的3种情绪的强度值均服从相同的正态分布N(0,2),并通过调整标准差σi(t)实现算法中的反馈机制。若个体某代的社会评价优于前一代,则表明该情绪起到了积极的影响,此时,增大该情绪正态分布的标准差以提高其被再次选中的概率;否则,减小标准差。即通过改变标准差来调节个体各情绪的强度,从而实现了个体对情绪的不同选择。被选中的情绪所对应正态分布的标准差的更新方式如下 (14) 式中 e为被选中的情绪。 柯西分布概率密度函数为 (15) 初始化时令所有个体的情绪服从柯西分布C(1,5),通过调整γ来改变情绪被选中的概率,其原理与3.2相同。参数γ的更新方式如下 (16) 式中 e为被选中的情绪。 利用北京二环的实测交通流数据,每2min采集一次。选择光华路至建国门桥为目标路段,取其2014年10月15日7:30~10:00的交通流数据进行实验,共有75组数据,前60组用于训练模型,后15组用于模型预测性能的测试。实验前,对交通流数据进行归一化处理 (17) 将原序列{Xi}转换为以0为均值,以1为振幅的归一化新序列 。 环路上,某一路段的交通流与其上下游路段密切相关,故设置BP神经网络的输入为目标路段及其上、下游各一个路段在t,t-1时刻的交通流,输出为目标路段在t+1时刻的交通流(t-1为前一时刻、t为当前时刻、t+1为后一时刻)。BP神经网络模型采用n-(2n+1)-1的典型3层结构,n为输入节点的个数(取6),训练次数为20000次,训练目标误差为0.0001,学习速率为0.05;社会群体规模为100,最大迭代次数1500次,个体学习因子均取2,个体社会状态范围为[-10,10];另外经多次测试,情绪阈值m1和m2分别取0.40,0.75时算法输出最优;用RMSE作为个体的社会评价值。 采用平均误差(AE)、平均绝对误差(MAE)、平均相对误差(MAPE)、均方误差(MSE)、均方根误差(RMSE)5类误差综合评价预测模型,计算如下 (18) (19) (20) 为了更好地说明该SEOBP预测模型的有效性,引入目前应用较为广泛的粒子群优化(particle swarm optimization,PSO)算法优化BP神经网络(PSOBP模型),同时将模拟退火技术(SA)加入到PSOBP模型中得到一种新的预测模型(SAPSOBP模型)。将上述2种模型以及BP模型与本文的SEOBP模型进行比较。PSO算法的粒子群规模、最大迭代次数等同SEO算法。 图1 4种模型的预测结果 分析图1(交通量每2min测量一次,共15组)、表1,得出结论如下: 1)BP模型的预测效果明显劣于其他3种模型,可见BP模型极易陷入局部最优,每种模型预测精度:10min>20min>30min,且随着预测时间的延长,预测精度下降加快,可以推断这些模型并不适合长时间的交通流预测。 2)在10min预测上,PSOBP的预测精度(从RMSE上看)相比BP模型提高了16.70%,可见PSO算法对BP神经网络性能的提高是有帮助的。 表1 4种预测模型的各项误差指标 由于模拟退火技术(SA)使粒子群按Metropolis准则在接受优化解的同时以一定概率接受恶化解,可加大信息吞吐量,这对粒子逃离局部极值区域是有益的,不过在本次实验中,SAPSOBP模型并没有在很大程度上提高预测精度,并且其在PSO基础上加入SA,使模型复杂化,对整个模型的收敛速度将有一定影响,该模型的总体性能不及SEOBP模型。 3)SEOBP模型在10 min中的预测精度(从RMSE上看)相比BP模型、PSOBP模型、SAPSOBP模型分别提高了43.30 %,31.94 %,20.87 %,不难看出,SEOBP模型能较好地改善预测性能。同样,在20,30 min的预测上,SEOBP模型的优势明显,可见,其对实测交通流的预测有效。 SEOBP模型与基于Levy分布、正态分布、柯西分布的SEO算法优化BP模型的预测结果,如图2。后3种模型分别记为LDSEOBP,NDSEOBP,CDSEOBP,为使结果更有效,后3种模型分别取15次实验结果的平均值。 图2 4种模型的预测结果 由以上可知:基于3种情绪随机选择策略的SEOBP模型均具有良好的预测性能,10 min的预测中,NDSEOBP模型的预测精度最高;20 min的预测中,NDSEOBP模型与LDSEOBP的预测精度相当,优于另外2种模型;30 min的预测上,CDSEOBP模型和NDSEOBP模型的预测精度要低于SEOBP模型、LDSEOBP模型,且后两者的预测精度相差较小。综合来看,LDSEOBP模型的预测性能更为优越,能够实现短时交通流更为精准的预测。 表2 基于不同分布的SEOBP模型的各项误差指标 通过引入新的群智能算法——SEO算法优化BP模型,并将其应用于北京二环实测交通流的预测,同时与BP模型、PSOBP模型、SAPSOBP模型对比,结果表明:该方法能较大程度地提高短时交通流预测精度,更有利于BP模型逃离局部极值区域,获得全局最优解。 SEO中情绪的线性更新方式存在一定不足,将基于Levy分布、正态分布、柯西分布的情绪随机选择策略应用到SEO算法中,综合分析表明:基于Levy分布的选择策略的预测效果更好,其对实测交通流具有更高的预测精度。下一步研究的重点是探讨社会群体规模、迭代次数、情绪阈值以及Levy分布参数等对预测精度的影响关系,并修正这些值,以期获得更好的短时交通流预测性能。 [1] Guo J,Huang W,Williams B.Adaptive Kalman filter approach for stochastic short-term traffic flow rate prediction and uncertainty quantification[J].Transport Res Part C,2014,43(1):50-64. [2] Hou Y,Praveen E,Carlos S.Traffic flow fore-casting for urban work zones[J].IEEE Transactions on Intelligent Transportation Systems,2015,16(4):1761- 1770. [3] Huang M L.Intersection traffic flow forecasting based on v-GSVR with a new hybrid evolutionary algorithm[J].Neurocomputing,2015,147:343-349. [4] Cui Z H,Cai X J.Using social cognitive optimization algorithm to solve nonlinear equations[C]∥Proc of 9th IEEE Int’l Conf on Cognitive Informatics,2010:199-203. [5] Wu J N,Cui Z H,Liu J.Using hybrid social emotional optimization algorithm with metropolis rule to solve nonlinear equa-tions[C]∥Proc of 10th IEEE I C on Cognitive Informatics & Cognitive Computing,2011:405-411. [6] Zhang Y Q,Zhang P L.Machine training and parameter settings with social emotional optimization algorithm for support vector machine[J].Pattern Recognition Letters,2015,54:36-42. Cui Z H,Cai X J.Optimal coverage configuration with social emotional optimization algorithm in wireless sensor networks.International Journal of Wireless and Mobile Computing,2011,5(1):43-47. Yang C X,Chen L C,Cui Z H.Solving redundancy optimization problem with social emotional optimization algorithm.International Journal of Computer Applications in Technology,2012,43(4):320-326. Cui Z H,Fan S J,Shi Z Z.Social emotional optimization algorithm with gaussian distribution for optimal coverage problem.Sensor Letters,2013,11(2):259-263. Cui Z H,Xu Y C.Social emotional optimization algorithm with Levy distribution.International Journal of Wireless and Mobile Computing,2012,5(4):394-400. Short-termtrafficflowforecastingbasedonSEOoptimizedneuralnetwork ZHANG Jun, HU Zhen-bo, ZHU Xin-shan, WANG Yuan-qiang (SchoolofElectricalEngineeringandAutomaton,TianjinUniversity,Tianjin300072,China) Using back propagation(BP) neural network in traffic flow predicting easy to fall into local optimum and speed of optimizing is slow.Therefore,using social emotional optimization(SEO)algorithm to optimize the parameters of BP network.In SEO,each individual represents a BP network and optimizing through cooperation and competition between individuals that having three emotions.To choose uncertain emotion with different probabilities,use three emotional random selection strategys based on Levy,normal and Cauchy distribution in different ways and this solution can make the update mode of emotion better simulate people’s normal psychological change.Experimental results show that compared with other forecasting models,these models are more advantageous to search the global optimal solution and the predicting precision can be effectively improved. urban traffic;short-term traffic flow forecasting;social emotional optimization(SEO)algorithm;traffic flow; back propagation(BP) neural network 10.13873/J.1000—9787(2017)10—0023—04 2016—09—10 TP 39.4 A 1000—9787(2017)10—0023—04 张 军(1964-),男,硕士,副教授,主要从事图像处理、智能交通研究工作。
2 SEO算法优化BP神经网络预测模型
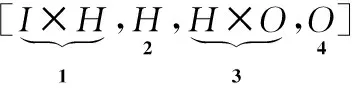

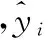
3 SEO算法中情绪的随机选择策略
3.1 基于Levy分布的SEO算法
3.2 基于正态分布的SEO算法
3.3 基于柯西分布的SEO算法

4 模型的实际应用
4.1 实验条件

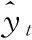
4.2 实验结果


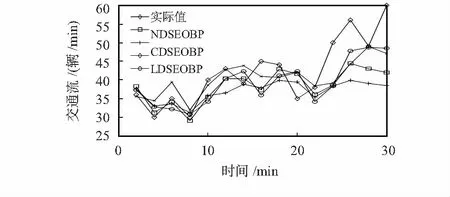

5 结 论

